Bisymmetric matrix

Short description: Square matrix symmetric about both its diagonal and anti-diagonal

Symmetry pattern of a bisymmetric 5 × 5 matrix

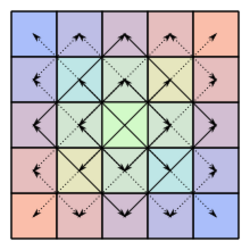
In mathematics, a bisymmetric matrix is a square matrix that is symmetric about both of its main diagonals. More precisely, an n × n matrix A is bisymmetric if it satisfies both A = A^T (it is its own transpose), and AJ = JA, where J is the n × n exchange matrix.

For example, any matrix of the form

[math]\displaystyle{ \begin{bmatrix} a & b & c & d & e \\ b & f & g & h & d \\ c & g & i & g & c \\ d & h & g & f & b \\ e & d & c & b & a \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} & a_{15} \\ a_{12} & a_{22} & a_{23} & a_{24} & a_{14} \\ a_{13} & a_{23} & a_{33} & a_{23} & a_{13} \\ a_{14} & a_{24} & a_{23} & a_{22} & a_{12} \\ a_{15} & a_{14} & a_{13} & a_{12} & a_{11} \end{bmatrix} }[/math]

is bisymmetric. The associated [math]\displaystyle{ 5\times 5 }[/math] exchange matrix for this example is

[math]\displaystyle{ J_{5} = \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \end{bmatrix} }[/math]

Properties

• Bisymmetric matrices are both symmetric centrosymmetric and symmetric persymmetric.
• The product of two bisymmetric matrices is a centrosymmetric matrix.
• Real-valued bisymmetric matrices are precisely those symmetric matrices whose eigenvalues remain the same aside from possible sign changes following pre- or post-multiplication by the exchange matrix.
• If A is a real bisymmetric matrix with distinct eigenvalues, then the matrices that commute with A must be bisymmetric.
• The inverse of bisymmetric matrices can be represented by recurrence formulas.