Cabibbo–Kobayashi–Maskawa matrix
| Flavour in particle physics |
|---|
| Flavour quantum numbers |
|
| Related quantum numbers |
|
| Combinations |
|
| Flavour mixing |
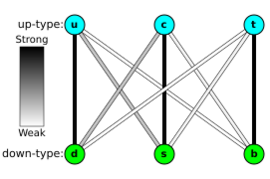
In the Standard Model of particle physics, the Cabibbo–Kobayashi–Maskawa matrix, CKM matrix, quark mixing matrix, or KM matrix is a unitary matrix which contains information on the strength of the flavour-changing weak interaction. Technically, it specifies the mismatch of quantum states of quarks when they propagate freely and when they take part in the weak interactions. It is important in the understanding of CP violation. This matrix was introduced for three generations of quarks by Makoto Kobayashi and Toshihide Maskawa, adding one generation to the matrix previously introduced by Nicola Cabibbo. This matrix is also an extension of the GIM mechanism, which only includes two of the three current families of quarks.
The matrix
Predecessor – the Cabibbo matrix

In 1963, Nicola Cabibbo introduced the Cabibbo angle (θc) to preserve the universality of the weak interaction.[1] Cabibbo was inspired by previous work by Murray Gell-Mann and Maurice Lévy,[2] on the effectively rotated nonstrange and strange vector and axial weak currents, which he references.[3]
In light of current concepts (quarks had not yet been proposed), the Cabibbo angle is related to the relative probability that down and strange quarks decay into up quarks ( |Vud|2 and |Vus|2 , respectively). In particle physics jargon, the object that couples to the up quark via charged-current weak interaction is a superposition of down-type quarks, here denoted by d′.[4] Mathematically this is:
- [math]\displaystyle{ d' = V_\mathrm{ud} \; d ~~ + ~~ V_\mathrm{us} \; s ~, }[/math]
or using the Cabibbo angle:
- [math]\displaystyle{ d' = \cos \theta_\mathrm{c} \; d ~~ + ~~ \sin \theta_\mathrm{c} \; s ~. }[/math]
Using the currently accepted values for |Vud| and |Vus| (see below), the Cabibbo angle can be calculated using
- [math]\displaystyle{ \tan\theta_\mathrm{c} = \frac{\, |V_\mathrm{us}| \,}{|V_\mathrm{ud}|} = \frac{0.22534}{0.97427} \quad \Rightarrow \quad \theta_\mathrm{c}= ~13.02^\circ ~. }[/math]
When the charm quark was discovered in 1974, it was noticed that the down and strange quark could decay into either the up or charm quark, leading to two sets of equations:
- [math]\displaystyle{ d' = V_\mathrm{ud} \; d ~~ + ~~ V_\mathrm{us} \; s ~, }[/math]
- [math]\displaystyle{ s' = V_\mathrm{cd} \; d ~~ + ~~ V_\mathrm{cs} \; s ~; }[/math]
or using the Cabibbo angle:
- [math]\displaystyle{ d' = ~~~ \cos{\theta_\mathrm{c}} \; d ~~+~~ \sin{\theta_\mathrm{c}} \; s ~, }[/math]
- [math]\displaystyle{ s' = - \sin{\theta_\mathrm{c}} \; d ~~+~~ \cos{\theta_\mathrm{c}} \; s ~. }[/math]
This can also be written in matrix notation as:
- [math]\displaystyle{ \begin{bmatrix} d' \\ s' \end{bmatrix} = \begin{bmatrix} V_\mathrm{ud} & V_\mathrm{us} \\ V_{cd} & V_{cs} \\ \end{bmatrix} \begin{bmatrix} d \\ s \end{bmatrix} ~, }[/math]
or using the Cabibbo angle
- [math]\displaystyle{ \begin{bmatrix} d' \\ s' \end{bmatrix} = \begin{bmatrix} ~~\cos{ \theta_\mathrm{c} } & \sin{ \theta_\mathrm{c} } \\ -\sin{\theta_\mathrm{c}} & \cos{\theta_\mathrm{c}}\\ \end{bmatrix} \begin{bmatrix} d \\ s \end{bmatrix}~, }[/math]
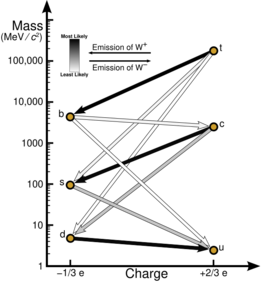
where the various |Vij|2 represent the probability that the quark of flavor j decays into a quark of flavor i. This 2×2 rotation matrix is called the "Cabibbo matrix", and was subsequently expanded to the 3×3 CKM matrix.
CKM matrix
In 1973, observing that CP-violation could not be explained in a four-quark model, Kobayashi and Maskawa generalized the Cabibbo matrix into the Cabibbo–Kobayashi–Maskawa matrix (or CKM matrix) to keep track of the weak decays of three generations of quarks:[5]
- [math]\displaystyle{ \begin{bmatrix} d' \\ s' \\ b' \end{bmatrix} = \begin{bmatrix} V_\mathrm{ud} & V_\mathrm{us} & V_\mathrm{ub} \\ V_\mathrm{cd} & V_\mathrm{cs} & V_\mathrm{cb} \\ V_\mathrm{td} & V_\mathrm{ts} & V_\mathrm{tb} \end{bmatrix} \begin{bmatrix} d \\ s \\ b \end{bmatrix}~. }[/math]
On the left are the weak interaction doublet partners of down-type quarks, and on the right is the CKM matrix, along with a vector of mass eigenstates of down-type quarks. The CKM matrix describes the probability of a transition from one flavour j quark to another flavour i quark. These transitions are proportional to |Vij|2.
As of 2023, the best determination of the individual magnitudes of the CKM matrix elements was:[6]
- [math]\displaystyle{ \begin{bmatrix} |V_{ud}| & |V_{us}| & |V_{ub}| \\ |V_{cd}| & |V_{cs}| & |V_{cb}| \\ |V_{td}| & |V_{ts}| & |V_{tb}| \end{bmatrix} = \begin{bmatrix} 0.97373 \pm 0.00031 & 0.2243 \pm 0.0008 & 0.00382 \pm 0.00020 \\ 0.221 \pm 0.004 & 0.975 \pm 0.006 & 0.0408 \pm 0.0014 \\ 0.0086 \pm 0.0002 & 0.0415 \pm 0.0009 & 1.014 \pm 0.029 \end{bmatrix}. }[/math]
Using those values, one can check the unitarity of the CKM matrix. In particular, we find that the first-row matrix elements give: [math]\displaystyle{ |V_\mathrm{ud}|^2 + |V_\mathrm{us}|^2 + |V_\mathrm{ub}|^2 = 0.9985 \pm 0.0007~; }[/math]
The difference from the theoretical value of 1 poses a tension of 2.2 standard deviations. Non-unitarity would be an indication of physics beyond the Standard Model.
The choice of usage of down-type quarks in the definition is a convention, and does not represent a physically preferred asymmetry between up-type and down-type quarks. Other conventions are equally valid: The mass eigenstates u, c, and t of the up-type quarks can equivalently define the matrix in terms of their weak interaction partners u′, c′, and t′. Since the CKM matrix is unitary, its inverse is the same as its conjugate transpose, which the alternate choices use; it appears as the same matrix, in a slightly altered form.
General case construction
To generalize the matrix, count the number of physically important parameters in this matrix V which appear in experiments. If there are N generations of quarks (2N flavours) then
- An N × N unitary matrix (that is, a matrix V such that V†V = I, where V† is the conjugate transpose of V and I is the identity matrix) requires N2 real parameters to be specified.
- 2N − 1 of these parameters are not physically significant, because one phase can be absorbed into each quark field (both of the mass eigenstates, and of the weak eigenstates), but the matrix is independent of a common phase. Hence, the total number of free variables independent of the choice of the phases of basis vectors is N2 − (2N − 1) = (N − 1)2.
- Of these, 1/2N(N − 1) are rotation angles called quark mixing angles.
- The remaining 1/2(N − 1)(N − 2) are complex phases, which cause CP violation.
N = 2
For the case N = 2, there is only one parameter, which is a mixing angle between two generations of quarks. Historically, this was the first version of CKM matrix when only two generations were known. It is called the Cabibbo angle after its inventor Nicola Cabibbo.
N = 3
For the Standard Model case (N = 3), there are three mixing angles and one CP-violating complex phase.[7]
Observations and predictions
Cabibbo's idea originated from a need to explain two observed phenomena:
- the transitions u ↔ d, e ↔ νe , and μ ↔ νμ had similar amplitudes.
- the transitions with change in strangeness ΔS = 1 had amplitudes equal to 1 /4 of those with ΔS = 0 .
Cabibbo's solution consisted of postulating weak universality (see below) to resolve the first issue, along with a mixing angle θc, now called the Cabibbo angle, between the d and s quarks to resolve the second.
For two generations of quarks, there can be no CP violating phases, as shown by the counting of the previous section. Since CP violations had already been seen in 1964, in neutral kaon decays, the Standard Model that emerged soon after clearly indicated the existence of a third generation of quarks, as Kobayashi and Maskawa pointed out in 1973. The discovery of the bottom quark at Fermilab (by Leon Lederman's group) in 1976 therefore immediately started off the search for the top quark, the missing third-generation quark.
Note, however, that the specific values that the angles take on are not a prediction of the standard model: They are free parameters. At present, there is no generally-accepted theory that explains why the angles should have the values that are measured in experiments.
Weak universality
The constraints of unitarity of the CKM-matrix on the diagonal terms can be written as
- [math]\displaystyle{ \sum_k |V_{jk}|^2 = \sum_k |V_{kj}|^2 = 1 }[/math]
separately for each generation j. This implies that the sum of all couplings of any one of the up-type quarks to all the down-type quarks is the same for all generations. This relation is called weak universality and was first pointed out by Nicola Cabibbo in 1967. Theoretically it is a consequence of the fact that all SU(2) doublets couple with the same strength to the vector bosons of weak interactions. It has been subjected to continuing experimental tests.
The unitarity triangles
The remaining constraints of unitarity of the CKM-matrix can be written in the form
- [math]\displaystyle{ \sum_k V_{ik}V^*_{jk} = 0 ~. }[/math]
For any fixed and different i and j, this is a constraint on three complex numbers, one for each k, which says that these numbers form the sides of a triangle in the complex plane. There are six choices of i and j (three independent), and hence six such triangles, each of which is called a unitary triangle. Their shapes can be very different, but they all have the same area, which can be related to the CP violating phase. The area vanishes for the specific parameters in the Standard Model for which there would be no CP violation. The orientation of the triangles depend on the phases of the quark fields.
A popular quantity amounting to twice the area of the unitarity triangle is the Jarlskog invariant (introduced by Cecilia Jarlskog in 1985),
- [math]\displaystyle{ J = c_{12}c_{13}^2 c_{23}s_{12}s_{13}s_{23}\sin \delta \approx 3\cdot10^{-5} ~. }[/math]
For Greek indices denoting up quarks and Latin ones down quarks, the 4-tensor [math]\displaystyle{ \;(\alpha,\beta;i,j)\equiv \operatorname{Im} (V_{\alpha i} V_{\beta j} V^*_{\alpha j} V_{\beta i}^{*}) \; }[/math] is doubly antisymmetric,
- [math]\displaystyle{ (\beta,\alpha;i,j) = -(\alpha,\beta;i,j)=(\alpha,\beta;j,i) ~. }[/math]
Up to antisymmetry, it only has 9 = 3 × 3 non-vanishing components, which, remarkably, from the unitarity of V, can be shown to be all identical in magnitude, that is,
- [math]\displaystyle{ (\alpha,\beta;i,j)= J ~ \begin{bmatrix} \;~~0 & \;~~1 & -1 \\ -1 & \;~~0 & \;~~1 \\ \;~~1 & -1 & \;~~0 \end{bmatrix}_{\alpha \beta} \otimes \begin{bmatrix} \;~~0 & \;~~1 & -1 \\ -1 & \;~~0 & \;~~1 \\ \;~~1 & -1 & \;~~0 \end{bmatrix}_{ij} \;, }[/math]
so that
- [math]\displaystyle{ J = (u,c;s,b) = (u,c;d,s) = (u,c;b,d) = (c,t;s,b) = (c,t;d,s) = (c,t;b,d) = (t,u;s,b) = (t,u;b,d) = (t,u;d,s) ~. }[/math]
Since the three sides of the triangles are open to direct experiment, as are the three angles, a class of tests of the Standard Model is to check that the triangle closes. This is the purpose of a modern series of experiments under way at the Japanese BELLE and the American BaBar experiments, as well as at LHCb in CERN, Switzerland.
Parameterizations
Four independent parameters are required to fully define the CKM matrix. Many parameterizations have been proposed, and three of the most common ones are shown below.
KM parameters
The original parameterization of Kobayashi and Maskawa used three angles ( θ1, θ2, θ3 ) and a CP-violating phase angle ( δ ).[5] θ1 is the Cabibbo angle. For brevity, the cosines and sines of the angles θk are denoted ck and sk, for k = 1, 2, 3 respectively.
- [math]\displaystyle{ \begin{bmatrix} c_1 & -s_1 c_3 & -s_1 s_3 \\ s_1 c_2 & c_1 c_2 c_3 - s_2 s_3 e^{i\delta} & c_1 c_2 s_3 + s_2 c_3 e^{i\delta}\\ s_1 s_2 & c_1 s_2 c_3 + c_2 s_3 e^{i\delta} & c_1 s_2 s_3 - c_2 c_3 e^{i\delta} \end{bmatrix}. }[/math]
"Standard" parameters
A "standard" parameterization of the CKM matrix uses three Euler angles ( θ12, θ23, θ13 ) and one CP-violating phase ( δ13 ).[8] θ12 is the Cabibbo angle. Couplings between quark generations j and k vanish if θjk = 0 . Cosines and sines of the angles are denoted cjk and sjk, respectively.
- [math]\displaystyle{ \begin{align} & \begin{bmatrix} 1 & 0 & 0 \\ 0 & c_{23} & s_{23} \\ 0 & -s_{23} & c_{23} \end{bmatrix} \begin{bmatrix} c_{13} & 0 & s_{13}e^{-i\delta_{13}} \\ 0 & 1 & 0 \\ -s_{13}e^{i\delta_{13}} & 0 & c_{13} \end{bmatrix} \begin{bmatrix} c_{12} & s_{12} & 0 \\ -s_{12} & c_{12} & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & = \begin{bmatrix} c_{12}c_{13} & s_{12} c_{13} & s_{13}e^{-i\delta_{13}} \\ -s_{12}c_{23} - c_{12}s_{23}s_{13}e^{i\delta_{13}} & c_{12}c_{23} - s_{12}s_{23}s_{13}e^{i\delta_{13}} & s_{23}c_{13}\\ s_{12}s_{23} - c_{12}c_{23}s_{13}e^{i\delta_{13}} & -c_{12}s_{23} - s_{12}c_{23}s_{13}e^{i\delta_{13}} & c_{23}c_{13} \end{bmatrix}. \end{align} }[/math]
The 2008 values for the standard parameters were:[9]
- θ12 = 13.04°±0.05°, θ13 = 0.201°±0.011°, θ23 = 2.38°±0.06°
and
- δ13 = 1.20±0.08 radians = 68.8°±4.5°.
Wolfenstein parameters
A third parameterization of the CKM matrix was introduced by Lincoln Wolfenstein with the four parameters λ, A, ρ, and η, which would all 'vanish' (would be zero) if there were no coupling.[10] The four Wolfenstein parameters have the property that all are of order 1 and are related to the 'standard' parameterization:
[math]\displaystyle{ \lambda = s_{12} ~, }[/math] [math]\displaystyle{ \lambda = s_{12} ~, }[/math] [math]\displaystyle{ A \lambda^2 = s_{23} ~, }[/math] [math]\displaystyle{ A = \frac{s_{23} }{\; s_{12}^2 \;} ~, }[/math] [math]\displaystyle{ A \lambda^3 ( \rho - i \eta ) = s_{13} e^{-i\delta} ~, \quad }[/math] [math]\displaystyle{ \rho = \operatorname\mathcal{R_e} \left\{ \frac{\; s_{13} \, e^{-i\delta} \;}{ s_{12} \, s_{23} } \right\} ~, \quad \eta = - \operatorname\mathcal{I_m} \left\{ \frac{\; s_{13} \, e^{-i\delta} \;}{ s_{12} \, s_{23} } \right\} ~. }[/math]
Although the Wolfenstein parameterization of the CKM matrix can be as exact as desired when carried to high order, it is mainly used for generating convenient approximations to the standard parameterization. The approximation to order λ3, good to better than 0.3% accuracy, is:
- [math]\displaystyle{ \begin{bmatrix} 1 - \tfrac{1}{2}\lambda^2 & \lambda & A\lambda^3(\rho-i\eta) \\ -\lambda & 1-\tfrac{1}{2}\lambda^2 & A\lambda^2 \\ A\lambda^3(1-\rho-i\eta) & -A\lambda^2 & 1 \end{bmatrix} + O(\lambda^4) ~. }[/math]
Rates of CP violation correspond to the parameters ρ and η.
Using the values of the previous section for the CKM matrix, as of 2008 the best determination of the Wolfenstein parameter values is:[11]
- λ = 0.2257+0.0009
−0.0010, A = 0.814+0.021
−0.022, ρ = 0.135+0.031
−0.016, and η = 0.349+0.015
−0.017.
Nobel Prize
In 2008, Kobayashi and Maskawa shared one half of the Nobel Prize in Physics "for the discovery of the origin of the broken symmetry which predicts the existence of at least three families of quarks in nature".[12] Some physicists were reported to harbor bitter feelings about the fact that the Nobel Prize committee failed to reward the work of Cabibbo, whose prior work was closely related to that of Kobayashi and Maskawa.[13] Asked for a reaction on the prize, Cabibbo preferred to give no comment.[14]
See also
- Formulation of the Standard Model and CP violations
- Quantum chromodynamics, flavour and strong CP problem
- Weinberg angle, a similar angle for Z and photon mixing
- Pontecorvo–Maki–Nakagawa–Sakata matrix, the equivalent mixing matrix for neutrinos
- Koide formula
References
- ↑ Cabibbo, N. (1963). "Unitary Symmetry and Leptonic Decays". Physical Review Letters 10 (12): 531–533. doi:10.1103/PhysRevLett.10.531. Bibcode: 1963PhRvL..10..531C.
- ↑ "The Axial Vector Current in Beta Decay". Il Nuovo Cimento 16 (4): 705–726. 1960. doi:10.1007/BF02859738. Bibcode: 1960NCim...16..705G.
- ↑ Maiani, L. (2009). "Sul premio Nobel per la fisica 2008". Il Nuovo Saggiatore 25 (1–2): 78. http://prometeo.sif.it:8080/papers/online/sag/025/01-02/pdf/78_opinioni.pdf. Retrieved 30 November 2010.
- ↑ Hughes, I.S. (1991). "Chapter 11.1 – Cabibbo Mixing". Elementary Particles (3rd ed.). Cambridge University Press. pp. 242–243. ISBN 978-0-521-40402-0. https://books.google.com/books?id=JN6qlZlGUG4C&q=cabbibo+angle&pg=PA242.
- ↑ 5.0 5.1 Kobayashi, M.; Maskawa, T. (1973). "CP-violation in the renormalizable theory of weak interaction". Progress of Theoretical Physics 49 (2): 652–657. doi:10.1143/PTP.49.652. Bibcode: 1973PThPh..49..652K.
- ↑ R.L. Workman et al. (Particle Data Group) (August 2022). "Review of Particle Physics (and 2023 update)". Progress of Theoretical and Experimental Physics 2022 (8): 083C01. doi:10.1093/ptep/ptac097. https://pdg.lbl.gov/. Retrieved 12 September 2023.
- ↑ Baez, J.C. (4 April 2011). "Neutrinos and the mysterious Pontecorvo-Maki-Nakagawa-Sakata matrix". http://math.ucr.edu/home/baez/neutrinos.html. "In fact, the Pontecorvo–Maki–Nakagawa–Sakata matrix actually affects the behavior of all leptons, not just neutrinos. Furthermore, a similar trick works for quarks – but then the matrix U is called the Cabibbo–Kobayashi–Maskawa matrix."
- ↑ Chau, L.L.; Keung, W.-Y. (1984). "Comments on the Parametrization of the Kobayashi-Maskawa Matrix". Physical Review Letters 53 (19): 1802–1805. doi:10.1103/PhysRevLett.53.1802. Bibcode: 1984PhRvL..53.1802C.
- ↑ Values obtained from values of Wolfenstein parameters in the 2008 Review of Particle Physics.
- ↑ "Parametrization of the Kobayashi-Maskawa Matrix". Physical Review Letters 51 (21): 1945–1947. 1983. doi:10.1103/PhysRevLett.51.1945. Bibcode: 1983PhRvL..51.1945W.
- ↑ Amsler, C.; Doser, M.; Antonelli, M.; Asner, D.M.; Babu, K.S.; Baer, H. et al. (2008). "The CKM Quark-Mixing Matrix". Physics Letters B. Review of Particles Physics 667 (1): 1–1340. doi:10.1016/j.physletb.2008.07.018. Bibcode: 2008PhLB..667....1A. http://pdg.lbl.gov/2008/reviews/kmmixrpp.pdf.
- ↑ "The Nobel Prize in Physics 2008" (Press release). The Nobel Foundation. 7 October 2008. Retrieved 24 November 2009.
- ↑ Jamieson, V. (7 October 2008). "Physics Nobel Snubs key Researcher". New Scientist. https://www.newscientist.com/article/dn14885-physics-nobel-snubs-key-researcher.html?DCMP=ILC-hmts&nsref=news8_head_dn14885.
- ↑ "Nobel, l'amarezza dei fisici italiani" (in it). Corriere della Sera. 7 October 2008. http://www.corriere.it/scienze_e_tecnologie/08_ottobre_07/nobel_fisica_italiani_traditi_d9993120-946d-11dd-a0d8-00144f02aabc.shtml.
Further reading and external links
- D.J. Griffiths (2008). Introduction to Elementary Particles (2nd ed.). John Wiley & Sons. ISBN 978-3-527-40601-2.
- B. Povh (1995). Particles and Nuclei: An Introduction to the Physical Concepts. Springer. ISBN 978-3-540-20168-7.
- I.I. Bigi, A.I. Sanda (2000). CP violation. Cambridge University Press. ISBN 978-0-521-44349-4.
- "Particle Data Group: The CKM quark-mixing matrix". http://pdg.lbl.gov/2013/reviews/rpp2012-rev-ckm-matrix.pdf.
- "Particle Data Group: CP violation in meson decays". http://pdg.lbl.gov/2013/reviews/rpp2012-rev-cp-violation.pdf.
- "The Babar experiment". http://www-public.slac.stanford.edu/babar/. at SLAC, California, and "the BELLE experiment". http://belle.kek.jp. at KEK, Japan.
 |