Unimodular matrix
In mathematics, a unimodular matrix M is a square integer matrix having determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N that is its inverse (these are equivalent under Cramer's rule). Thus every equation Mx = b, where M and b both have integer components and M is unimodular, has an integer solution. The n × n unimodular matrices form a group called the n × n general linear group over [math]\displaystyle{ \mathbb{Z} }[/math], which is denoted [math]\displaystyle{ \operatorname{GL}_n(\mathbb{Z}) }[/math].
Examples of unimodular matrices
Unimodular matrices form a subgroup of the general linear group under matrix multiplication, i.e. the following matrices are unimodular:
- Identity matrix
- The inverse of a unimodular matrix
- The product of two unimodular matrices
Other examples include:
- Pascal matrices
- Permutation matrices
- the three transformation matrices in the ternary tree of primitive Pythagorean triples
- Certain transformation matrices for rotation, shearing (both with determinant 1) and reflection (determinant −1).
- The unimodular matrix used (possibly implicitly) in lattice reduction and in the Hermite normal form of matrices.
- The Kronecker product of two unimodular matrices is also unimodular. This follows since [math]\displaystyle{ \det(A \otimes B) = (\det A)^q (\det B)^p, }[/math] where p and q are the dimensions of A and B, respectively.
Total unimodularity
A totally unimodular matrix[1] (TU matrix) is a matrix for which every square non-singular submatrix is unimodular. Equivalently, every square submatrix has determinant 0, +1 or −1. A totally unimodular matrix need not be square itself. From the definition it follows that any submatrix of a totally unimodular matrix is itself totally unimodular (TU). Furthermore it follows that any TU matrix has only 0, +1 or −1 entries. The converse is not true, i.e., a matrix with only 0, +1 or −1 entries is not necessarily unimodular. A matrix is TU if and only if its transpose is TU.
Totally unimodular matrices are extremely important in polyhedral combinatorics and combinatorial optimization since they give a quick way to verify that a linear program is integral (has an integral optimum, when any optimum exists). Specifically, if A is TU and b is integral, then linear programs of forms like [math]\displaystyle{ \{\min c^\top x \mid Ax \ge b, x \ge 0\} }[/math] or [math]\displaystyle{ \{\max c^\top x \mid Ax \le b\} }[/math] have integral optima, for any c. Hence if A is totally unimodular and b is integral, every extreme point of the feasible region (e.g. [math]\displaystyle{ \{x \mid Ax \ge b\} }[/math]) is integral and thus the feasible region is an integral polyhedron.
Common totally unimodular matrices
1. The unoriented incidence matrix of a bipartite graph, which is the coefficient matrix for bipartite matching, is totally unimodular (TU). (The unoriented incidence matrix of a non-bipartite graph is not TU.) More generally, in the appendix to a paper by Heller and Tompkins,[2] A.J. Hoffman and D. Gale prove the following. Let [math]\displaystyle{ A }[/math] be an m by n matrix whose rows can be partitioned into two disjoint sets [math]\displaystyle{ B }[/math] and [math]\displaystyle{ C }[/math]. Then the following four conditions together are sufficient for A to be totally unimodular:
- Every entry in [math]\displaystyle{ A }[/math] is 0, +1, or −1;
- Every column of [math]\displaystyle{ A }[/math] contains at most two non-zero (i.e., +1 or −1) entries;
- If two non-zero entries in a column of [math]\displaystyle{ A }[/math] have the same sign, then the row of one is in [math]\displaystyle{ B }[/math], and the other in [math]\displaystyle{ C }[/math];
- If two non-zero entries in a column of [math]\displaystyle{ A }[/math] have opposite signs, then the rows of both are in [math]\displaystyle{ B }[/math], or both in [math]\displaystyle{ C }[/math].
It was realized later that these conditions define an incidence matrix of a balanced signed graph; thus, this example says that the incidence matrix of a signed graph is totally unimodular if the signed graph is balanced. The converse is valid for signed graphs without half edges (this generalizes the property of the unoriented incidence matrix of a graph).[3]
2. The constraints of maximum flow and minimum cost flow problems yield a coefficient matrix with these properties (and with empty C). Thus, such network flow problems with bounded integer capacities have an integral optimal value. Note that this does not apply to multi-commodity flow problems, in which it is possible to have fractional optimal value even with bounded integer capacities.
3. The consecutive-ones property: if A is (or can be permuted into) a 0-1 matrix in which for every row, the 1s appear consecutively, then A is TU. (The same holds for columns since the transpose of a TU matrix is also TU.) [4]
4. Every network matrix is TU. The rows of a network matrix correspond to a tree T = (V, R), each of whose arcs has an arbitrary orientation (it is not necessary that there exist a root vertex r such that the tree is "rooted into r" or "out of r").The columns correspond to another set C of arcs on the same vertex set V. To compute the entry at row R and column C = st, look at the s-to-t path P in T; then the entry is:
- +1 if arc R appears forward in P,
- −1 if arc R appears backwards in P,
- 0 if arc R does not appear in P.
See more in Schrijver (2003).
5. Ghouila-Houri showed that a matrix is TU iff for every subset R of rows, there is an assignment [math]\displaystyle{ s:R \to \pm1 }[/math] of signs to rows so that the signed sum [math]\displaystyle{ \sum_{r \in R} s(r)r }[/math] (which is a row vector of the same width as the matrix) has all its entries in [math]\displaystyle{ \{0,\pm1\} }[/math] (i.e. the row-submatrix has discrepancy at most one). This and several other if-and-only-if characterizations are proven in Schrijver (1998).
6. Hoffman and Kruskal[5] proved the following theorem. Suppose [math]\displaystyle{ G }[/math] is a directed graph without 2-dicycles, [math]\displaystyle{ P }[/math] is the set of all dipaths in [math]\displaystyle{ G }[/math], and [math]\displaystyle{ A }[/math] is the 0-1 incidence matrix of [math]\displaystyle{ V(G) }[/math] versus [math]\displaystyle{ P }[/math]. Then [math]\displaystyle{ A }[/math] is totally unimodular if and only if every simple arbitrarily-oriented cycle in [math]\displaystyle{ G }[/math] consists of alternating forwards and backwards arcs.
7. Suppose a matrix has 0-([math]\displaystyle{ \pm }[/math]1) entries and in each column, the entries are non-decreasing from top to bottom (so all −1s are on top, then 0s, then 1s are on the bottom). Fujishige showed[6] that the matrix is TU iff every 2-by-2 submatrix has determinant in [math]\displaystyle{ 0, \pm1 }[/math].
8. Seymour (1980)[7] proved a full characterization of all TU matrices, which we describe here only informally. Seymour's theorem is that a matrix is TU if and only if it is a certain natural combination of some network matrices and some copies of a particular 5-by-5 TU matrix.
Concrete examples
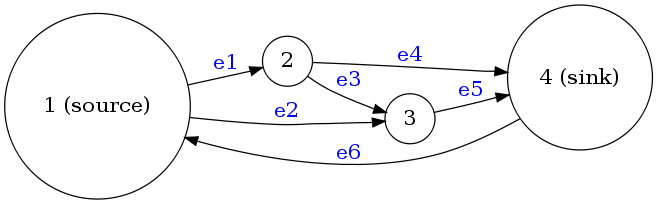
1. The following matrix is totally unimodular:
- [math]\displaystyle{ A=\left[\begin{array}{rrrrrr} -1 & -1 & 0 & 0 & 0 & +1\\ +1 & 0 & -1 & -1 & 0 & 0\\ 0 & +1 & +1 & 0 & -1 & 0\\ 0 & 0 & 0 & +1 & +1 & -1 \end{array}\right]. }[/math]
This matrix arises as the coefficient matrix of the constraints in the linear programming formulation of the maximum flow problem on the following network:
2. Any matrix of the form
- [math]\displaystyle{ A=\left[\begin{array}{ccccc} & \vdots & & \vdots \\ \dotsb & +1 & \dotsb & +1 & \dotsb \\ & \vdots & & \vdots \\ \dotsb & +1 & \dotsb & -1 & \dotsb \\ & \vdots & & \vdots \end{array}\right]. }[/math]
is not totally unimodular, since it has a square submatrix of determinant −2.
Abstract linear algebra
Abstract linear algebra considers matrices with entries from any commutative ring [math]\displaystyle{ R }[/math], not limited to the integers. In this context, a unimodular matrix is one that is invertible over the ring; equivalently, whose determinant is a unit. This group is denoted [math]\displaystyle{ \operatorname{GL}_n(R) }[/math].[8] A rectangular [math]\displaystyle{ k }[/math]-by-[math]\displaystyle{ m }[/math] matrix is said to be unimodular if it can be extended with [math]\displaystyle{ m-k }[/math] rows in [math]\displaystyle{ R^m }[/math] to a unimodular square matrix.[9][10][11]
Over a field, unimodular has the same meaning as non-singular. Unimodular here refers to matrices with coefficients in some ring (often the integers) which are invertible over that ring, and one uses non-singular to mean matrices that are invertible over the field.
See also
Notes
- ↑ The term was coined by Claude Berge, see Hoffman, A.J.; Kruskal, J. (2010), "Introduction to Integral Boundary Points of Convex Polyhedra", in M. Jünger, 50 Years of Integer Programming, 1958-2008, Springer-Verlag, pp. 49–50
- ↑ Heller, I.; Tompkins, C.B. (1956), "An Extension of a Theorem of Dantzig's", in Kuhn, H.W.; Tucker, A.W., Linear Inequalities and Related Systems, Annals of Mathematics Studies, 38, Princeton (NJ): Princeton University Press, pp. 247–254
- ↑ T. Zaslavsky (1982), "Signed graphs," Discrete Applied Mathematics 4, pp. 401–406.
- ↑ Fulkerson, D. R.; Gross, O. A. (1965). "Incidence matrices and interval graphs." (in en). Pacific Journal of Mathematics 15 (3): 835–855. ISSN 0030-8730. https://projecteuclid.org/euclid.pjm/1102995572.
- ↑ Hoffman, A.J.; Kruskal, J.B. (1956), "Integral Boundary Points of Convex Polyhedra", in Kuhn, H.W.; Tucker, A.W., Linear Inequalities and Related Systems, Annals of Mathematics Studies, 38, Princeton (NJ): Princeton University Press, pp. 223–246
- ↑ Fujishige, Satoru (1984), "A System of Linear inequalities with a Submodular Function on (0, ±1) Vectors", Linear Algebra and Its Applications 63: 253–266, doi:10.1016/0024-3795(84)90147-2
- ↑ Seymour, P. D. (1980), "Decomposition of regular matroids", Journal of Combinatorial Theory, Series B 28 (3): 305–359, doi:10.1016/0095-8956(80)90075-1
- ↑ Lang, Serge (2002). Algebra (rev. 3rd ed.). Springer. p. 510, Section XIII.3. ISBN 0-387-95385-X.
- ↑ Rosenthal, J.; Maze, G.; Wagner, U. (2011), Natural Density of Rectangular Unimodular Integer Matrices, Linear Algebra and its applications, 434, Elsevier, pp. 1319–1324
- ↑ Micheli, G.; Schnyder, R. (2016), The density of unimodular matrices over integrally closed subrings of function fields, Contemporary Developments in Finite Fields and Applications, World Scientific, pp. 244–253
- ↑ Guo, X.; Yang, G. (2013), The probability of rectangular unimodular matrices over Fq [x], Linear algebra and its applications, Elsevier, pp. 2675–2682
References
- Papadimitriou, Christos H.; Steiglitz, Kenneth (1998), Combinatorial Optimization: Algorithms and Complexity, Mineola, N.Y.: Dover Publications, p. 316, ISBN 978-0-486-40258-1, https://books.google.com/books?id=cDY-joeCGoIC&pg=PA316
- Alexander Schrijver (1998), Theory of Linear and Integer Programming. John Wiley & Sons, ISBN:0-471-98232-6 (mathematical)
- Alexander Schrijver (2003), Combinatorial Optimization: Polyhedra and Efficiency, Springer
External links
- Mathematical Programming Glossary by Harvey J. Greenberg
- Unimodular Matrix from MathWorld
- Software for testing total unimodularity by M. Walter and K. Truemper
 |