Clar's rule
In organic and physical organic chemistry, Clar's rule is an empirical rule that relates the chemical stability of a molecule with its aromaticity. It was introduced in 1972 by the Austrian organic chemist Erich Clar in his book The Aromatic Sextet. The rule states that given a polycyclic aromatic hydrocarbon, the resonance structure most important to characterize its properties is that with the largest number of aromatic π-sextets i.e. benzene-like moieties. [1]
The rule
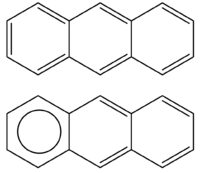
In general, the chemical structure of a given polycyclic aromatic hydrocarbon admits more than one resonance structure: these are sometimes referred to as Kekulé resonance structures. Some of such structures may contain aromatic π-sextets, namely groups of six π-electrons localized in a benzene-like moiety and separated by adjacent rings by formal C–C bonds. An aromatic π-sextet can be represented by a circle, as in the case of the anthracene molecule. Clar's rule states that for a benzenoid polycyclic aromatic hydrocarbon (i.e. with only hexagonal rings), the resonance structure with the largest number of disjoint aromatic π-sextets is the most important to characterize its chemical and physical properties. Such resonance structure is called the Clar structure. In other words, a polycyclic aromatic hydrocarbon with a given number of π-sextets is more stable than its isomers with less π-sextets.[1][2] In 1984, Glidewell and Lloyd provided an extension of Clar's rule to polycyclic aromatic hydrocarbons containing rings of any size.[3] More recently, Clar's rule was further extended to biradicaloids in their singlet state.[4]
Writing a Clar structure
When writing a Clar structure, the following rules must be satisfied:[5]
- each vertex of the molecular graph representing the polycyclic aromatic hydrocarbon either belongs to a double bond or a circle;
- such double bonds and circles never join;
- there are no rings with three double bonds, since they are always represented by circles; moreover, the number of circles in the graph is maximized;
- when a ring with a circle is adjacent to a ring with two double bonds, an arrow is drawn from the former to the latter ring.
Some observations about these rules are worth to be put into evidence. Following Clar,[1] rules at points 1 and 2 imply that circles can never be in adjacent rings; rule at point 3 means that only four options are viable for rings, namely (i) having only one double bond, (ii) having two double bonds, (iii) having a circle, or (iv) being empty, i.e. having no double bonds; finally, the arrow mentioned in the rule at point 4 can be interpreted in terms of mobility of π-sextets (in this case we speak of migrating π-sextets) or, equivalently, of a quantum-mechanical resonance between different Clar structures.[5]
Examples
In the following, Clar's rule is applied to three different cases.
The resonance structures of phenanthrene
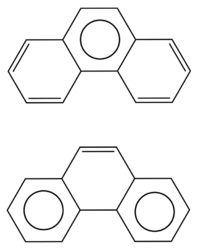
According to the rules exposed above, the phenanthrene molecule admits two different resonance structures: one of them presents a single circle in the center of the molecule, with each of the two adjacent rings having two double bonds; the other one has the two peripheral rings each with one circle, and the central ring with one double bond. According to Clar's rule, this last resonance structure gives the most important contribution to the determination of the properties of phenanthrene.[2][6]
The migrating π-sextet of anthracene
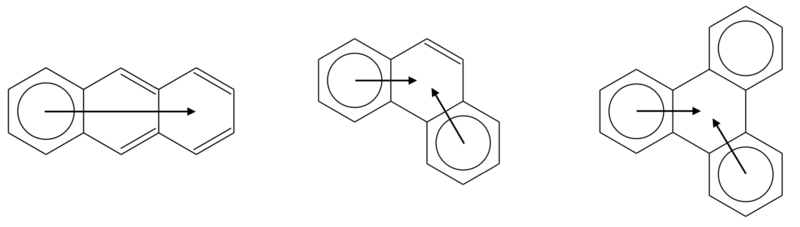
The anthracene molecule admits three resonance structures, each with a circle in one ring and two sets of double bonds in the other two. Following the rule at point 4 exposed above, anthracene is better described by a superposition of these three equivalent structures, and an arrow is drawn to indicate the presence of a migrating π-sextet. Following the same line of reasoning, one can find migrating π-sextets in other molecules of the acene series, such as tetracene, pentacene, and hexacene.[2]
The role of angular rings
Fusing angular rings around a benzene moiety leads to an increase in stability. The Clar structure of anthracene, for instance, has only one π-sextet, but moving one ring into the angular position phenanthrene is obtained, the Clar structure of which carries two circles instead of one – notice that this molecule can be thought of as a benzene moiety with two fused rings; a third ring can be fused to obtain triphenylene, with three aromatic π-sextets in its Clar structure. The chemical stability of these molecules is greatly influenced by the degree of aromaticity of their Clar structures. As a result, while anthracene reacts with maleic acid, phenanthrene does not, and triphenylene is the most stable species of these three.[1]
Experimental evidence and applications
Since its formal statement in 1972, Clar's rule has received a vast amount of experimental evidence. The dependence of the color and reactivity of some small polycyclic aromatic hydrocarbons on the number of π-sextets in their structures is reported by Clar himself in his seminal contribution.[1] Similarly, it was shown that the HOMO-LUMO gap, and therefore the color, of a series of heptacatafusenes depends on the number of π-sextets.[5] Clar's rule has also been supported by experimental results about the distribution of π-electrons in polycyclic aromatic hydrocarbons,[7] valence bond calculations,[8] and nucleus independent chemical shift studies.[9]
Clar's rule is widely applied in the fields of chemistry and materials science. For instance, Clar's rule can be used to predict several properties of graphene nanoribbons.[10] Aromatic π-sextets play an important part in the determination of the ground state of open shell biradical-type structures.[11] , Clar's rule can rationalize the observed a decrease of the bandgap of holey graphenes with increasing size.[12]
Limitations
Despite the experimental support mentioned above, Clar's rule suffers from some limitations. In the first place, Clar's rule is formulated only for species with hexagonal rings,[13] and thus it cannot be applied to species having rings different from the benzene moiety, even though an extension of the rule to molecules with rings of any dimension has been provided by Glidewell and Lloyd.[13] Secondly, if more than one Clar structure exist for a given species, Clar's rule does not allow to determine the relative importance of each of them in the determination of the physicochemical properties.[6] Finally, it is important to mention that exceptions to the Clar's rule exist, such as in the case of triangulenes.[14]
See also
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Erich Clar (1972). "The Aromatic Sextet". in D. Rondia. Mobile Source Emissions Including Policyclic Organic Species. John Wiley & Sons. pp. 49–58. doi:10.1007/978-94-009-7197-4_4. ISBN 978-94-009-7199-8.
- ↑ 2.0 2.1 2.2 , Wikidata Q38208843
- ↑ , Wikidata Q112830674
- ↑ , Wikidata Q44732390
- ↑ 5.0 5.1 5.2 , Wikidata Q112828750
- ↑ 6.0 6.1 , Wikidata Q56387336
- ↑ , Wikidata Q112830992
- ↑ , Wikidata Q43905733
- ↑ , Wikidata Q112831105
- ↑ , Wikidata Q83008058
- ↑ , Wikidata Q44732390
- ↑ , Wikidata Q92685111
- ↑ 13.0 13.1 , Wikidata Q61857678
- ↑ , Wikidata Q100996684
 |