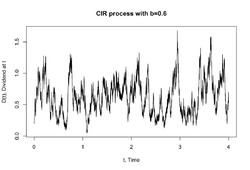
Cox–Ingersoll–Ross model

Short description: Stochastic model for the evolution of financial interest rates

Three trajectories of CIR processes

In mathematical finance, the Cox–Ingersoll–Ross (CIR) model describes the evolution of interest rates. It is a type of "one factor model" (short-rate model) as it describes interest rate movements as driven by only one source of market risk. The model can be used in the valuation of interest rate derivatives. It was introduced in 1985 by John C. Cox, Jonathan E. Ingersoll and Stephen A. Ross as an extension of the Vasicek model.

The model

CIR process

The CIR model describes the instantaneous interest rate [math]\displaystyle{ r_t }[/math] with a Feller square-root process, whose stochastic differential equation is

[math]\displaystyle{ dr_t = a(b-r_t)\, dt + \sigma\sqrt{r_t}\, dW_t, }[/math]

where [math]\displaystyle{ W_t }[/math] is a Wiener process (modelling the random market risk factor) and [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math], and [math]\displaystyle{ \sigma\, }[/math] are the parameters. The parameter [math]\displaystyle{ a }[/math] corresponds to the speed of adjustment to the mean [math]\displaystyle{ b }[/math], and [math]\displaystyle{ \sigma\, }[/math] to volatility. The drift factor, [math]\displaystyle{ a(b-r_t) }[/math], is exactly the same as in the Vasicek model. It ensures mean reversion of the interest rate towards the long run value [math]\displaystyle{ b }[/math], with speed of adjustment governed by the strictly positive parameter [math]\displaystyle{ a }[/math].

The standard deviation factor, [math]\displaystyle{ \sigma \sqrt{r_t} }[/math], avoids the possibility of negative interest rates for all positive values of [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math]. An interest rate of zero is also precluded if the condition

[math]\displaystyle{ 2 a b \geq \sigma^2 \, }[/math]

is met. More generally, when the rate ([math]\displaystyle{ r_t }[/math]) is close to zero, the standard deviation ([math]\displaystyle{ \sigma \sqrt{r_t} }[/math]) also becomes very small, which dampens the effect of the random shock on the rate. Consequently, when the rate gets close to zero, its evolution becomes dominated by the drift factor, which pushes the rate upwards (towards equilibrium).

In the case [math]\displaystyle{ 2 a b =\sigma^2 \, }[/math], the Feller square-root process can be obtained from the square of an Ornstein–Uhlenbeck process. It is ergodic and possesses a stationary distribution. It is used in the Heston model to model stochastic volatility.

Distribution

• Future distribution

The distribution of future values of a CIR process can be computed in closed form:

[math]\displaystyle{ r_{t+T} = \frac{Y}{2c}, }[/math]

where [math]\displaystyle{ c=\frac{2a}{(1 - e^{-aT})\sigma^2} }[/math], and Y is a non-central chi-squared distribution with [math]\displaystyle{ \frac{4ab}{\sigma^2} }[/math] degrees of freedom and non-centrality parameter [math]\displaystyle{ 2 c r_te^{-aT} }[/math]. Formally the probability density function is:

[math]\displaystyle{ f(r_{t+T};r_t,a,b,\sigma)=c\,e^{-u-v} \left (\frac{v}{u}\right)^{q/2} I_{q}(2\sqrt{uv}), }[/math]

where [math]\displaystyle{ q = \frac{2ab}{\sigma^2}-1 }[/math], [math]\displaystyle{ u = c r_t e^{-aT} }[/math], [math]\displaystyle{ v = c r_{t+T} }[/math], and [math]\displaystyle{ I_{q}(2\sqrt{uv}) }[/math] is a modified Bessel function of the first kind of order [math]\displaystyle{ q }[/math].

• Asymptotic distribution

Due to mean reversion, as time becomes large, the distribution of [math]\displaystyle{ r_{\infty} }[/math] will approach a gamma distribution with the probability density of:

[math]\displaystyle{ f(r_\infty;a,b,\sigma)=\frac{\beta^\alpha}{\Gamma(\alpha)}r_\infty^{\alpha-1}e^{-\beta r_\infty}, }[/math]

where [math]\displaystyle{ \beta = 2a/\sigma^2 }[/math] and [math]\displaystyle{ \alpha = 2ab/\sigma^2 }[/math].

Derivation of asymptotic distribution

To derive the asymptotic distribution [math]\displaystyle{ p_{\infty} }[/math] for the CIR model, we must use the Fokker-Planck equation: [math]\displaystyle{ {\partial p\over{\partial t}} + {\partial\over{\partial r}}[a(b-r)p] = {1\over{2}}\sigma^{2}{\partial^{2}\over{\partial r^{2}}}(rp) }[/math] Our interest is in the particular case when [math]\displaystyle{ \partial_{t}p \rightarrow 0 }[/math], which leads to the simplified equation: [math]\displaystyle{ a(b-r)p_{\infty} = {1\over{2}}\sigma^{2}\left(p_{\infty} + r{dp_{\infty}\over{dr}} \right) }[/math] Defining [math]\displaystyle{ \alpha = 2ab/\sigma^{2} }[/math] and [math]\displaystyle{ \beta = 2a/\sigma^{2} }[/math] and rearranging terms leads to the equation: [math]\displaystyle{ {\alpha-1\over{r}} - \beta = {d\over{dr}} \log p_{\infty} }[/math] Integrating shows us that: [math]\displaystyle{ p_{\infty} \propto r^{\alpha-1}e^{-\beta r} }[/math] Over the range [math]\displaystyle{ p_{\infty} \in (0,\infty] }[/math], this density describes a gamma distribution. Therefore, the asymptotic distribution of the CIR model is a gamma distribution.

Properties

• Mean reversion,
• Level dependent volatility ([math]\displaystyle{ \sigma \sqrt{r_t} }[/math]),
• For given positive [math]\displaystyle{ r_0 }[/math] the process will never touch zero, if [math]\displaystyle{ 2 a b \geq\sigma^2 }[/math]; otherwise it can occasionally touch the zero point,
• [math]\displaystyle{ \operatorname E[r_t\mid r_0]=r_0 e^{-at} + b (1-e^{-at}) }[/math], so long term mean is [math]\displaystyle{ b }[/math],
• [math]\displaystyle{ \operatorname{Var}[r_t\mid r_0]=r_0 \frac{\sigma^2}{a} (e^{- a t}-e^{-2a t}) + \frac{b \sigma^2}{2 a}(1-e^{- a t})^2. }[/math]

Calibration

• Ordinary least squares

The continuous SDE can be discretized as follows

[math]\displaystyle{ r_{t+\Delta t}-r_t = a (b-r_t)\,\Delta t + \sigma\, \sqrt{r_t \Delta t} \varepsilon_t, }[/math]

which is equivalent to

[math]\displaystyle{ \frac{r_{t+\Delta t}-r_t}{\sqrt r_t} =\frac{ab\Delta t}{\sqrt r_t}-a \sqrt r_t\Delta t + \sigma\, \sqrt{\Delta t} \varepsilon_t, }[/math]

provided [math]\displaystyle{ \varepsilon_t }[/math] is n.i.i.d. (0,1). This equation can be used for a linear regression.

• Martingale estimation
• Maximum likelihood

Simulation

Stochastic simulation of the CIR process can be achieved using two variants:

• Discretization
• Exact

Bond pricing

Under the no-arbitrage assumption, a bond may be priced using this interest rate process. The bond price is exponential affine in the interest rate:

[math]\displaystyle{ P(t,T) = A(t,T) e^{-B(t,T) r_t}\! }[/math]

where

[math]\displaystyle{ A(t,T) = \left(\frac{2h e^{(a+h)(T-t)/2}}{2h + (a+h)(e^{h(T-t)} -1)}\right)^{2ab/\sigma^2} }[/math]

[math]\displaystyle{ B(t,T) = \frac{2(e^{h(T-t)}-1)}{2h+(a+h)(e^{h(T-t)}-1)} }[/math]

[math]\displaystyle{ h = \sqrt{a^2+2\sigma^2} }[/math]

Extensions

The CIR model uses a special case of a basic affine jump diffusion, which still permits a closed-form expression for bond prices. Time varying functions replacing coefficients can be introduced in the model in order to make it consistent with a pre-assigned term structure of interest rates and possibly volatilities. The most general approach is in Maghsoodi (1996). A more tractable approach is in Brigo and Mercurio (2001b) where an external time-dependent shift is added to the model for consistency with an input term structure of rates.

A significant extension of the CIR model to the case of stochastic mean and stochastic volatility is given by Lin Chen (1996) and is known as Chen model. A more recent extension for handling cluster volatility, negative interest rates and different distributions is the so-called "CIR #" by Orlando, Mininni and Bufalo (2018, 2019, 2020, 2021, 2023) and a simpler extension focussing on negative interest rates was proposed by Di Francesco and Kamm (2021, 2022), which are referred to as the CIR- and CIR-- models.

See also

• Hull–White model
• Vasicek model
• Chen model

Further References

• Hull, John C. (2003). Options, Futures and Other Derivatives. Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-009056-5. https://archive.org/details/optionsfuturesot00hull_1. 
• Cox, J.C., J.E. Ingersoll and S.A. Ross (1985). "A Theory of the Term Structure of Interest Rates". Econometrica 53 (2): 385–407. doi:10.2307/1911242. 
• Maghsoodi, Y. (1996). "Solution of the extended CIR Term Structure and Bond Option Valuation". Mathematical Finance 6 (6): 89–109. doi:10.1111/j.1467-9965.1996.tb00113.x. 
• Damiano Brigo; Fabio Mercurio (2001). Interest Rate Models — Theory and Practice with Smile, Inflation and Credit (2nd ed. 2006 ed.). Springer Verlag. ISBN 978-3-540-22149-4. 
• Brigo, Damiano; Fabio Mercurio (2001b). "A deterministic-shift extension of analytically tractable and time-homogeneous short rate models". Finance & Stochastics 5 (3): 369–388. doi:10.1007/PL00013541. http://ideas.repec.org/a/spr/finsto/v5y2001i3p369-387.html. 
• Open Source library implementing the CIR process in python
• Orlando, Giuseppe; Mininni, Rosa Maria; Bufalo, Michele (2020). "Forecasting interest rates through Vasicek and CIR models: A partitioning approach" (in en). Journal of Forecasting 39 (4): 569–579. doi:10.1002/for.2642. ISSN 1099-131X. 

de:Wurzel-Diffusionsprozess#Cox-Ingersoll-Ross-Modell