Equirectangular projection

Short description: Cylindrical equidistant map projection

Equirectangular projection of the world; the standard parallel is the equator (plate carrée projection).

Equirectangular projection with Tissot's indicatrix of deformation and with the standard parallels lying on the equator

True-colour satellite image of Earth in equirectangular projection

Height map of planet Earth at 2km per pixel, including oceanic bathymetry information, normalized as 8-bit grayscale. Because of its easy conversion between x, y pixel information and lat-lon, maps like these are very useful for software map renderings.

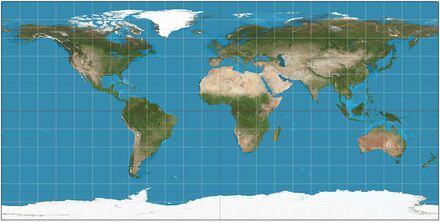
The equirectangular projection (also called the equidistant cylindrical projection or la carte parallélogrammatique projection), and which includes the special case of the plate carrée projection (also called the geographic projection, lat/lon projection, or plane chart), is a simple map projection attributed to Marinus of Tyre, who Ptolemy claims invented the projection about AD 100.

The projection maps meridians to vertical straight lines of constant spacing (for meridional intervals of constant spacing), and circles of latitude to horizontal straight lines of constant spacing (for constant intervals of parallels). The projection is neither equal area nor conformal. Because of the distortions introduced by this projection, it has little use in navigation or cadastral mapping and finds its main use in thematic mapping. In particular, the plate carrée has become a standard for global raster datasets, such as Celestia, NASA World Wind, the USGS Astrogeology Research Program, and Natural Earth, because of the particularly simple relationship between the position of an image pixel on the map and its corresponding geographic location on Earth or other spherical solar system bodies. In addition it is frequently used in panoramic photography to represent a spherical panoramic image.

Definition

The forward projection transforms spherical coordinates into planar coordinates. The reverse projection transforms from the plane back onto the sphere. The formulae presume a spherical model and use these definitions:

• [math]\displaystyle{ \lambda }[/math] is the longitude of the location to project;
• [math]\displaystyle{ \varphi }[/math] is the latitude of the location to project;
• [math]\displaystyle{ \varphi_1 }[/math] are the standard parallels (north and south of the equator) where the scale of the projection is true;
• [math]\displaystyle{ \varphi_0 }[/math] is the central parallel of the map;
• [math]\displaystyle{ \lambda_0 }[/math] is the central meridian of the map;
• [math]\displaystyle{ x }[/math] is the horizontal coordinate of the projected location on the map;
• [math]\displaystyle{ y }[/math] is the vertical coordinate of the projected location on the map;
• [math]\displaystyle{ R }[/math] is the radius of the globe.

Longitude and latitude variables are defined here in terms of radians.

Forward

[math]\displaystyle{ \begin{align} x &= R (\lambda - \lambda_0) \cos \varphi_1\\ y &= R (\varphi - \varphi_0) \end{align} }[/math]

The plate carrée (French, for flat square), is the special case where [math]\displaystyle{ \varphi_1 }[/math] is zero. This projection maps x to be the value of the longitude and y to be the value of the latitude, and therefore is sometimes called the latitude/longitude or lat/lon(g) projection. Despite sometimes being called "unprojected", it is actually projected.

When the [math]\displaystyle{ \varphi_1 }[/math] is not zero, such as Marinus's [math]\displaystyle{ \varphi_1=36 }[/math], or Ronald Miller's [math]\displaystyle{ \varphi_1=(37.5, 43.5, 50.5) }[/math], the projection can portray particular latitudes of interest at true scale.

While a projection with equally spaced parallels is possible for an ellipsoidal model, it would no longer be equidistant because the distance between parallels on an ellipsoid is not constant. More complex formulae can be used to create an equidistant map whose parallels reflect the true spacing.

Reverse

[math]\displaystyle{ \begin{align} \lambda &= \frac{x} {R \cos \varphi_1} + \lambda_0\\ \varphi &= \frac{y} {R} + \varphi_0 \end{align} }[/math]

Alternative names

In spherical panorama viewers, usually:

• [math]\displaystyle{ \lambda }[/math] is called "yaw";
• [math]\displaystyle{ \varphi }[/math] is called "pitch";

where both are defined in degrees.

See also

• Cartography
• Cassini projection
• Gall–Peters projection (mentions a resolution rejecting the use of all rectangular world maps)
• List of map projections
• Mercator projection
• 360 video projection
• Wikimedia Gallery of Equirectangular World Maps

External links

• Global MODIS based satellite map The blue marble: land surface, ocean color, and sea ice.
• Table of examples and properties of all common projections, from radicalcartography.net.
• Panoramic Equirectangular Projection, PanoTools wiki.
• Equidistant Cylindrical (Plate Carrée) in proj4