Winkel tripel projection
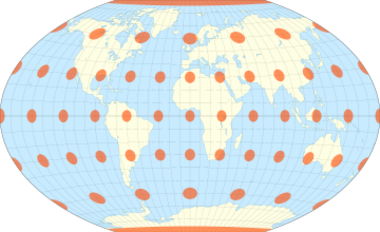
The Winkel tripel projection (Winkel III), a modified azimuthal[1] map projection of the world, is one of three projections proposed by German cartographer Oswald Winkel (7 January 1874 – 18 July 1953) in 1921. The projection is the arithmetic mean of the equirectangular projection and the Aitoff projection:[2] The name tripel (German for 'triple') refers to Winkel's goal of minimizing three kinds of distortion: area, direction, and distance.[3]
Algorithm
- [math]\displaystyle{ \begin{align} x &= \frac{1}{2} \left(\lambda \cos \varphi_1 + \frac{2 \cos \varphi \sin \frac{\lambda}{2}}{\operatorname{sinc} \alpha}\right), \\ y &= \frac{1}{2} \left(\varphi + \frac{\sin \varphi}{\operatorname{sinc} \alpha}\right), \end{align} }[/math]
where λ is the longitude relative to the central meridian of the projection, φ is the latitude, φ1 is the standard parallel for the equirectangular projection, sinc is the unnormalized cardinal sine function, and
- [math]\displaystyle{ \alpha = \arccos\left(\cos\varphi \cos \frac{\lambda}{2} \right). }[/math]
In his proposal, Winkel set
- [math]\displaystyle{ \varphi_1 = \arccos \frac{2}{\pi}. }[/math]
A closed-form inverse mapping does not exist, and computing the inverse numerically requires the use of iterative methods.[4]
Comparison with other projections
David M. Goldberg and J. Richard Gott III showed that the Winkel tripel fares better against several other projections analyzed against their measures of distortion, producing minimal distance, Tissot indicatrix ellipticity and area errors, and the least skew of any of the projections they studied.[5] By a different metric, Capek's "Q", the Winkel tripel ranked ninth among a hundred map projections of the world, behind the common Eckert IV projection and Robinson projections.[6]
In 1998, the Winkel tripel projection replaced the Robinson projection as the standard projection for world maps made by the National Geographic Society.[3] Many educational institutes and textbooks soon followed National Geographic's example in adopting the projection, most of which still utilize it.[7][8]
See also
References
- ↑ Snyder, John P. (1989). An album of map projections. USGS Professional Paper 1453. Washington, D.C.: Government Printing Office. p. 164.
- ↑ Snyder, John P. (1993). Flattening the Earth: Two Thousand Years of Map Projections. Chicago: University of Chicago Press. pp. 231–232. ISBN 0-226-76747-7. https://books.google.com/books?id=0UzjTJ4w9yEC&dq=winkel&pg=PA282. Retrieved 2011-11-14.
- ↑ 3.0 3.1 "Winkel Tripel Projections". Winkel.org. http://www.winkel.org/other/Winkel%20Tripel%20Projections.htm.
- ↑ Ipbüker, Cengizhan; Bildirici, I.Öztug (2002). "A General Algorithm for the Inverse Transformation of Map Projections Using Jacobian Matrices". Third International Symposium Mathematical & Computational Applications September 4–6, 2002. Konya, Turkey. Selcuk, Turkey. pp. 175–182. http://atlas.selcuk.edu.tr/paperdb/papers/130.pdf.
- ↑ Goldberg, David M.; Gott III, J. Richard (2007). "Flexion and Skewness in Map Projections of the Earth". Cartographica 42 (4): 297–318. doi:10.3138/carto.42.4.297. http://www.physics.drexel.edu/~goldberg/projections/goldberg_gott.pdf. Retrieved 2011-11-14.
- ↑ Capek, Richard (2001). "Which is the best projection for the world map?". Proceedings of the 20th International Cartographic Conference (Beijing, China) 5: 3084–93. https://icaci.org/files/documents/ICC_proceedings/ICC2001/icc2001/file/f24014.pdf. Retrieved 2018-11-15.
- ↑ "NG Maps Print Collection – World Political Map (Bright Colored)". National Geographic Society. https://www.nationalgeographic.com/maps/. "This latest world map ... features the Winkel Tripel projection to reduce the distortion of land masses as they near the poles."
- ↑ "Selecting a Map Projection – National Geographic Education". National Geographic Society. http://education.nationalgeographic.com/education/media/selecting-map-projection/?ar_a=1.
External links
 |  |
