Snyder equal-area projection

Short description: Equal-area polyhedral map projection

Snyder equal-area projection is a polyhedral map projection used in the ISEA (Icosahedral Snyder Equal Area) discrete global grids. It is named for John P. Snyder, who developed the projection in the 1990s.

It is a modified Lambert azimuthal equal-area projection, most often applied to a polyhedral globe consisting of an icosahedron.

With the dual tiling system is possible to transform the big triangular faces (gray) into small centered-hexagons (red), and vice versa.

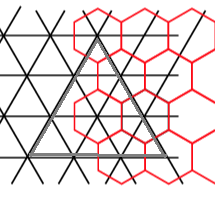
Use in the ISEA model

As stated by Carr at al. article, page 32:

The S in ISEA refers to John P. Snyder. He came out of retirement specifically to address projection problems with the original EMAP grid (see Snyder, 1992). He developed the equal area projection that underlies the gridding system.

ISEA grids are simple in concept. Begin with a Snyder Equal Area projection to a regular icosahedron (...) inscribed in a sphere. In each of the 20 equilateral triangle faces of the icosahedron inscribe a hexagon by dividing each triangle edge into thirds (...). Then project the hexagon back onto the sphere using the Inverse Snyder Icosahedral equal area projection. This yields a coarse-resolution equal area grid called the resolution 1 grid. It consists of 20 hexagons on the surface of the sphere and 12 pentagons centered on the 12 vertices of the icosahedron.