Proof without words
In mathematics, a proof without words (or visual proof) is an illustration of an identity or mathematical statement which can be demonstrated as self-evident by a diagram without any accompanying explanatory text. Such proofs can be considered more elegant than formal or mathematically rigorous proofs due to their self-evident nature.[1] When the diagram demonstrates a particular case of a general statement, to be a proof, it must be generalisable.[2]
A proof without words is not the same as a mathematical proof, because it omits the details of the logical argument it illustrates. However, it can provide valuable intuitions to the viewer that can help them formulate or better understand a true proof.
Examples
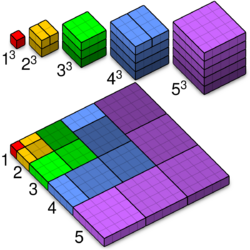
Sum of odd numbers
The statement that the sum of all positive odd numbers up to 2n − 1 is a perfect square—more specifically, the perfect square n2—can be demonstrated by a proof without words.[3]
In one corner of a grid, a single block represents 1, the first square. That can be wrapped on two sides by a strip of three blocks (the next odd number) to make a 2 × 2 block: 4, the second square. Adding a further five blocks makes a 3 × 3 block: 9, the third square. This process can be continued indefinitely.
Pythagorean theorem
The Pythagorean theorem that [math]\displaystyle{ a^2 + b^2 = c^2 }[/math] can be proven without words.[4]
One method of doing so is to visualise a larger square of sides [math]\displaystyle{ a+b }[/math], with four right-angled triangles of sides [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math] and [math]\displaystyle{ c }[/math] in its corners, such that the space in the middle is a diagonal square with an area of [math]\displaystyle{ c^2 }[/math]. The four triangles can be rearranged within the larger square to split its unused space into two squares of [math]\displaystyle{ a^2 }[/math] and [math]\displaystyle{ b^2 }[/math].[5]
Jensen's inequality
Jensen's inequality can also be proven graphically. A dashed curve along the X axis is the hypothetical distribution of X, while a dashed curve along the Y axis is the corresponding distribution of Y values. The convex mapping Y(X) increasingly "stretches" the distribution for increasing values of X.[6]
Usage
Mathematics Magazine and the College Mathematics Journal run a regular feature titled "Proof without words" containing, as the title suggests, proofs without words.[3] The Art of Problem Solving and USAMTS websites run Java applets illustrating proofs without words.[7][8]
Compared to formal proofs
For a proof to be accepted by the mathematical community, it must logically show how the statement it aims to prove follows totally and inevitably from a set of assumptions.[9] A proof without words might imply such an argument, but it does not make one directly, so it cannot take the place of a formal proof where one is required.[10][11] Rather, mathematicians use proofs without words as illustrations and teaching aids for ideas that have already been proven formally.[12][13]
See also
- Pizza theorem – Equality of areas of a sliced disk
- Philosophy:Philosophy of mathematics
- Proof theory – Branch of mathematical logic
- Visual calculus – Visual mathematical proofs
Notes
- ↑ Dunham 1994, p. 120
- ↑ Weisstein, Eric W.. "Proof without Words". http://mathworld.wolfram.com/ProofwithoutWords.html. Retrieved on 2008-6-20
- ↑ Jump up to: 3.0 3.1 Dunham 1994, p. 121
- ↑ Nelsen 1997, p. 3
- ↑ Benson, Donald. The Moment of Proof : Mathematical Epiphanies, pp. 172–173 (Oxford University Press, 1999).
- ↑ McShane, E. J. (1937), "Jensen's Inequality", Bulletin of the American Mathematical Society (American Mathematical Society) 43 (8): 527, doi:10.1090/S0002-9904-1937-06588-8
- ↑ Gallery of Proofs, Art of Problem Solving, http://artofproblemsolving.com/articles/proof-without-words, retrieved 2015-05-28
- ↑ Gallery of Proofs, USA Mathematical Talent Search, http://usamts.org/Gallery/G_Gallery.php, retrieved 2015-05-28
- ↑ Lang, Serge (1971). Basic Mathematics. Reading, Massachusetts: Addison-Wesley Publishing Company. p. 94. "We always try to keep clearly in mind what we assume and what we prove. By a 'proof' we mean a sequence of statements each of which is either assumed, or follows from the preceding statements by a rule of deduction, which is itself assumed."
- ↑ Benson, Steve; Addington, Susan; Arshavsky, Nina; Cuoco; Al; Goldenberg, E. Paul; Karnowski, Eric (October 6, 2004). Facilitator's Guide to Ways to Think About Mathematics (Illustrated ed.). Corwin Press. p. 78. ISBN 9781412905206. https://books.google.com/books?id=PW80dP3YN2MC&dq=%22proof+without+words%22&pg=PA78. "Proofs without words are not really proofs, strictly speaking, since details are typically lacking."
- ↑ Spivak, Michael (2008). Calculus (4th ed.). Houston, Texas: Publish or Perish, Inc.. p. 138. ISBN 978-0-914098-91-1. https://books.google.com/books?id=7JKVu_9InRUC&q=%22basing+the+argument+on+a+geometric+picture+is+not+a+proof%22&pg=PA136. "Basing the argument on a geometric picture is not a proof, however..."
- ↑ Benson, Steve; Addington, Susan; Arshavsky, Nina; Cuoco; Al; Goldenberg, E. Paul; Karnowski, Eric (October 6, 2004). Facilitator's Guide to Ways to Think About Mathematics (Illustrated ed.). Corwin Press. p. 78. ISBN 9781412905206. https://books.google.com/books?id=PW80dP3YN2MC&dq=%22proof+without+words%22&pg=PA78. "However, since most proofs without words are visual in nature, they often provide a reminder or hint of what's missing."
- ↑ Schulte, Tom (January 12, 2011). "Proofs without Words: Exercises in Visual Thinking (review)". MAA Reviews (The Mathematical Association of America). https://www.maa.org/press/maa-reviews/proofs-without-words-exercises-in-visual-thinking. Retrieved October 26, 2022. "This slim collection of varied visual 'proofs' (a term, it can be argued, loosely applied here) is entertaining and enlightening. I personally find such representations engaging and stimulating aids to that 'aha!' moment when symbolic argument seems not to clarify.".
References
- Dunham, William (1994), The Mathematical Universe, John Wiley and Sons, ISBN 0-471-53656-3, https://archive.org/details/mathematicaluniv0000dunh
- Nelsen, Roger B. (1997), Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, pp. 160, ISBN 978-0-88385-700-7
- Nelsen, Roger B. (2000), Proofs without Words II: More Exercises in Visual Thinking, Mathematical Association of America, pp. 142, ISBN 0-88385-721-9, https://archive.org/details/proofswithoutwor0000nels/page/142
- Gulley, Ned (March 4, 2010), Shure, Loren, ed., Nicomachus's Theorem, Matlab Central, http://blogs.mathworks.com/loren/2010/03/04/nichomachuss-theorem/.
 |




