Semidirect product

Short description: Operation in group theory

In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product. There are two closely related concepts of semidirect product:

an inner semidirect product is a particular way in which a group can be made up of two subgroups, one of which is a normal subgroup.
an outer semidirect product is a way to construct a new group from two given groups by using the Cartesian product as a set and a particular multiplication operation.

As with direct products, there is a natural equivalence between inner and outer semidirect products, and both are commonly referred to simply as semidirect products.

For finite groups, the Schur–Zassenhaus theorem provides a sufficient condition for the existence of a decomposition as a semidirect product (also known as splitting extension).

Inner semidirect product definitions

Given a group $G$ with identity element $e$ , a subgroup $H$ , and a normal subgroup $N ◁ G$ , the following statements are equivalent:

$G$ is the product of subgroups, $G = NH$ , and these subgroups have trivial intersection: $N \cap H = {e}$ .
For every $g \in G$ , there are unique $n \in N$ and $h \in H$ such that $g = nh$ .
For every $g \in G$ , there are unique $h \in H$ and $n \in N$ such that $g = hn$ .
The composition $π \circ i$ of the natural embedding $i : H \to G$ with the natural projection $π : G \to G / N$ is an isomorphism between $H$ and the quotient group $G / N$ .
There exists a homomorphism $G \to H$ that is the identity on $H$ and whose kernel is $N$ . In other words, there is a split exact sequence

[math]\displaystyle{ 1 \to N \to G \to H \to 1 }[/math]

of groups (which is also known as group extension of [math]\displaystyle{ H }[/math] by [math]\displaystyle{ N }[/math]).

If any of these statements holds (and hence all of them hold, by their equivalence), we say $G$ is the semidirect product of $N$ and $H$ , written

[math]\displaystyle{ G = N \rtimes H }[/math] or [math]\displaystyle{ G = H \ltimes N, }[/math]

or that $G$ splits over $N$ ; one also says that $G$ is a semidirect product of $H$ acting on $N$ , or even a semidirect product of $H$ and $N$ . To avoid ambiguity, it is advisable to specify which is the normal subgroup.

Inner and outer semidirect products

Let us first consider the inner semidirect product. In this case, for a group [math]\displaystyle{ G }[/math], consider its normal subgroup $N$ and the subgroup $H$ (not necessarily normal). Assume that the conditions on the list above hold. Let [math]\displaystyle{ \operatorname{Aut}(N) }[/math] denote the group of all automorphisms of $N$ , which is a group under composition. Construct a group homomorphism [math]\displaystyle{ \varphi \colon H \to \operatorname{Aut}(N) }[/math] defined by conjugation,

[math]\displaystyle{ \varphi(h)(n) = hnh^{-1} }[/math], for all

h

in

H

and

n

in

N

.

The expression [math]\displaystyle{ \varphi(h) }[/math] is often written as [math]\displaystyle{ \varphi_h }[/math] for brevity. In this way we can construct a group [math]\displaystyle{ G'=(N,H) }[/math] with group operation defined as

[math]\displaystyle{ (n_1, h_1) \cdot (n_2, h_2) = (n_1 \varphi(h_1)(n_2),\, h_1 h_2) = (n_1 \varphi_{h_1}(n_2),\, h_1 h_2) }[/math] for

n 1, n 2

in

N

and

h 1, h 2

in

H

.

The subgroups $N$ and $H$ determine $G$ up to isomorphism, as we will show later. In this way, we can construct the group $G$ from its subgroups. This kind of construction is called an inner semidirect product (also known as internal semidirect product^[1]).

Let us now consider the outer semidirect product. Given any two groups $N$ and $H$ and a group homomorphism $φ : H \to Aut(N)$ , we can construct a new group $N ⋊ φ H$ , called the outer semidirect product of $N$ and $H$ with respect to $φ$ , defined as follows:^[2]

The underlying set is the Cartesian product $N \times H$ .
The group operation [math]\displaystyle{ \bullet }[/math] is determined by the homomorphism $φ$ :
[math]\displaystyle{ \begin{align} \bullet : (N \rtimes_\varphi H) \times (N \rtimes_\varphi H) &\to N \rtimes_\varphi H\\ (n_1, h_1) \bullet (n_2, h_2) &= (n_1 \varphi(h_1)(n_2),\, h_1 h_2) = (n_1 \varphi_{h_1}(n_2),\, h_1 h_2) \end{align} }[/math]
for $n 1, n 2$ in $N$ and $h 1, h 2$ in $H$ .

This defines a group in which the identity element is $(e N, e H)$ and the inverse of the element $(n, h)$ is $(φ h -1 (n -1), h -1)$ . Pairs $(n, e H)$ form a normal subgroup isomorphic to $N$ , while pairs $(e N, h)$ form a subgroup isomorphic to $H$ . The full group is a semidirect product of those two subgroups in the sense given earlier.

Conversely, suppose that we are given a group $G$ with a normal subgroup $N$ and a subgroup $H$ , such that every element $g$ of $G$ may be written uniquely in the form $g = nh$ where $n$ lies in $N$ and $h$ lies in $H$ . Let $φ : H \to Aut(N)$ be the homomorphism (written $φ (h) = φ h$ ) given by

[math]\displaystyle{ \varphi_h(n) = hnh^{-1} }[/math]

for all $n \in N, h \in H$ .

Then $G$ is isomorphic to the semidirect product $N ⋊ φ H$ . The isomorphism $λ : G \to N ⋊ φ H$ is well defined by $λ (a) = λ (nh) = (n, h)$ due to the uniqueness of the decomposition $a = nh$ .

In $G$ , we have

[math]\displaystyle{ (n_1 h_1)(n_2 h_2) = n_1 h_1 n_2(h_1^{-1}h_1) h_2 = (n_1 \varphi_{h_1}(n_2))(h_1 h_2) }[/math]

Thus, for $a = n 1 h 1$ and $b = n 2 h 2$ we obtain

[math]\displaystyle{ \begin{align} \lambda(ab) & = \lambda(n_1 h_1 n_2 h_2) = \lambda(n_1 \varphi_{h_1} (n_2) h_1 h_2) = (n_1 \varphi_{h_1} (n_2), h_1 h_2) = (n_1, h_1) \bullet (n_2, h_2) \\[5pt] & = \lambda(n_1 h_1) \bullet \lambda(n_2 h_2) = \lambda(a) \bullet \lambda(b), \end{align} }[/math]

which proves that $λ$ is a homomorphism. Since $λ$ is obviously an epimorphism and monomorphism, then it is indeed an isomorphism. This also explains the definition of the multiplication rule in $N ⋊ φ H$ .

The direct product is a special case of the semidirect product. To see this, let $φ$ be the trivial homomorphism (i.e., sending every element of $H$ to the identity automorphism of $N$ ) then $N ⋊ φ H$ is the direct product $N \times H$ .

A version of the splitting lemma for groups states that a group $G$ is isomorphic to a semidirect product of the two groups $N$ and $H$ if and only if there exists a short exact sequence

[math]\displaystyle{ 1 \longrightarrow N \,\overset{\beta}{\longrightarrow}\, G \,\overset{\alpha}{\longrightarrow}\, H \longrightarrow 1 }[/math]

and a group homomorphism $γ : H \to G$ such that $α \circ γ = id H$ , the identity map on $H$ . In this case, $φ : H \to Aut(N)$ is given by $φ (h) = φ h$ , where

[math]\displaystyle{ \varphi_h(n) = \beta^{-1}(\gamma(h)\beta(n)\gamma(h^{-1})). }[/math]

Examples

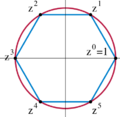
Dihedral group

The dihedral group $D 2 n$ with $2 n$ elements is isomorphic to a semidirect product of the cyclic groups $C n$ and $C 2$ .^[3] Here, the non-identity element of $C 2$ acts on $C n$ by inverting elements; this is an automorphism since $C n$ is abelian. The presentation for this group is:

[math]\displaystyle{ \langle a,\;b \mid a^2 = e,\; b^n = e,\; aba^{-1} = b^{-1}\rangle. }[/math]

Cyclic groups

More generally, a semidirect product of any two cyclic groups $C m$ with generator $a$ and $C n$ with generator $b$ is given by one extra relation, $aba -1 = b k$ , with $k$ and $n$ coprime, and [math]\displaystyle{ k^m\equiv 1 \pmod{n} }[/math];^[3] that is, the presentation:^[3]

[math]\displaystyle{ \langle a,\;b \mid a^m = e,\;b^n = e,\;aba^{-1} = b^k\rangle. }[/math]

If $r$ and $m$ are coprime, $a r$ is a generator of $C m$ and $a r ba -r = b k r$ , hence the presentation:

[math]\displaystyle{ \langle a,\;b \mid a^m = e,\;b^n = e,\;aba^{-1} = b^{k^{r}}\rangle }[/math]

gives a group isomorphic to the previous one.

Holomorph of a group

One canonical example of a group expressed as a semi-direct product is the holomorph of a group. This is defined as

[math]\displaystyle{ \operatorname{Hol}(G)=G\rtimes \operatorname{Aut}(G) }[/math]

where [math]\displaystyle{ \text{Aut}(G) }[/math] is the automorphism group of a group [math]\displaystyle{ G }[/math] and the structure map [math]\displaystyle{ \phi }[/math] comes from the right action of [math]\displaystyle{ \text{Aut}(G) }[/math] on [math]\displaystyle{ G }[/math]. In terms of multiplying elements, this gives the group structure

[math]\displaystyle{ (g,\alpha)(h,\beta)=(g(\phi(\alpha)\cdot h),\alpha\beta). }[/math]

Fundamental group of the Klein bottle

The fundamental group of the Klein bottle can be presented in the form

[math]\displaystyle{ \langle a,\;b \mid aba^{-1} = b^{-1}\rangle. }[/math]

and is therefore a semidirect product of the group of integers, [math]\displaystyle{ \mathbb{Z} }[/math], with [math]\displaystyle{ \mathbb{Z} }[/math]. The corresponding homomorphism $φ: [math]\displaystyle{ \mathbb{Z} }[/math] → Aut([math]\displaystyle{ \mathbb{Z} }[/math])$ is given by $φ (h)(n) = (-1) h n$ .

Upper triangular matrices

The group [math]\displaystyle{ \mathbb{T}_n }[/math] of upper triangular matrices^{[clarification needed]} with non-zero determinant, that is with non-zero entries on the diagonal, has a decomposition into the semidirect product [math]\displaystyle{ \mathbb{T}_n \cong \mathbb{U}_n \rtimes \mathbb{D}_n }[/math]^[4] where [math]\displaystyle{ \mathbb{U}_n }[/math] is the subgroup of matrices with only [math]\displaystyle{ 1 }[/math]'s on the diagonal, which is called the upper unitriangular matrix group, and [math]\displaystyle{ \mathbb{D}_n }[/math] is the subgroup of diagonal matrices.
The group action of [math]\displaystyle{ \mathbb{D}_n }[/math] on [math]\displaystyle{ \mathbb{U}_n }[/math] is induced by matrix multiplication. If we set

[math]\displaystyle{ A = \begin{bmatrix} x_1 & 0 & \cdots & 0 \\ 0 & x_2 & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & x_n \end{bmatrix} }[/math] and [math]\displaystyle{ B = \begin{bmatrix} 1 & a_{12} & a_{13} & \cdots & a_{1n} \\ 0 & 1 & a_{23} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{bmatrix} }[/math]

then their matrix product is

[math]\displaystyle{ AB = \begin{bmatrix} x_1 & x_1a_{12} & x_1a_{13} & \cdots & x_1a_{1n} \\ 0 & x_2 & x_2a_{23} & \cdots & x_2a_{2n} \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & x_n \end{bmatrix}. }[/math]

This gives the induced group action [math]\displaystyle{ m:\mathbb{D}_n\times \mathbb{U}_n \to \mathbb{U}_n }[/math]

[math]\displaystyle{ m(A,B) = \begin{bmatrix} 1 & x_1a_{12} & x_1a_{13} & \cdots & x_1a_{1n} \\ 0 & 1 & x_2a_{23} & \cdots & x_2a_{2n} \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{bmatrix}. }[/math]

A matrix in [math]\displaystyle{ \mathbb{T}_n }[/math] can be represented by matrices in [math]\displaystyle{ \mathbb{U}_n }[/math] and [math]\displaystyle{ \mathbb{D}_n }[/math]. Hence [math]\displaystyle{ \mathbb{T}_n \cong \mathbb{U}_n \rtimes \mathbb{D}_n }[/math].

Group of isometries on the plane

The Euclidean group of all rigid motions (isometries) of the plane (maps $f: [math]\displaystyle{ \mathbb{R} }[/math]2 → [math]\displaystyle{ \mathbb{R} }[/math]2$ such that the Euclidean distance between $x$ and $y$ equals the distance between $f (x)$ and $f (y)$ for all $x$ and $y$ in [math]\displaystyle{ \mathbb{R}^2 }[/math]) is isomorphic to a semidirect product of the abelian group [math]\displaystyle{ \mathbb{R}^2 }[/math] (which describes translations) and the group $O(2)$ of orthogonal $2 \times 2$ matrices (which describes rotations and reflections that keep the origin fixed). Applying a translation and then a rotation or reflection has the same effect as applying the rotation or reflection first and then a translation by the rotated or reflected translation vector (i.e. applying the conjugate of the original translation). This shows that the group of translations is a normal subgroup of the Euclidean group, that the Euclidean group is a semidirect product of the translation group and $O(2)$ , and that the corresponding homomorphism $φ: O(2) → Aut([math]\displaystyle{ \mathbb{R} }[/math]2)$ is given by matrix multiplication: $φ (h)(n) = hn$ .

Orthogonal group O(n)

The orthogonal group $O(n)$ of all orthogonal real $n \times n$ matrices (intuitively the set of all rotations and reflections of $n$ -dimensional space that keep the origin fixed) is isomorphic to a semidirect product of the group $SO(n)$ (consisting of all orthogonal matrices with determinant $1$ , intuitively the rotations of $n$ -dimensional space) and $C 2$ . If we represent $C 2$ as the multiplicative group of matrices ${I, R}$ , where $R$ is a reflection of $n$ -dimensional space that keeps the origin fixed (i.e., an orthogonal matrix with determinant $-1$ representing an involution), then $φ : C 2 \to Aut(SO(n))$ is given by $φ (H)(N) = HNH -1$ for all H in $C 2$ and $N$ in $SO(n)$ . In the non-trivial case ( $H$ is not the identity) this means that $φ (H)$ is conjugation of operations by the reflection (in 3-dimensional space a rotation axis and the direction of rotation are replaced by their "mirror image").

Semi-linear transformations

The group of semilinear transformations on a vector space $V$ over a field [math]\displaystyle{ \mathbb{K} }[/math], often denoted $ΓL(V)$ , is isomorphic to a semidirect product of the linear group $GL(V)$ (a normal subgroup of $ΓL(V)$ ), and the automorphism group of [math]\displaystyle{ \mathbb{K} }[/math].

Crystallographic groups

In crystallography, the space group of a crystal splits as the semidirect product of the point group and the translation group if and only if the space group is symmorphic. Non-symmorphic space groups have point groups that are not even contained as subset of the space group, which is responsible for much of the complication in their analysis.^[5]

Non-examples

Of course, every simple group cannot be expressed as a semi-direct product, but there are a few common counterexamples containing a non-trivial normal subgroup as well. Note that although not every group [math]\displaystyle{ G }[/math] can be expressed as a split extension of [math]\displaystyle{ H }[/math] by [math]\displaystyle{ A }[/math], it turns out that such a group can be embedded into the wreath product [math]\displaystyle{ A\wr H }[/math] by the universal embedding theorem.

Z₄

The cyclic group [math]\displaystyle{ \mathbb{Z}_4 }[/math] is not a simple group since it has a subgroup of order 2, namely [math]\displaystyle{ \{0,2\} \cong \mathbb{Z}_2 }[/math] is a subgroup and their quotient is [math]\displaystyle{ \mathbb{Z}_2 }[/math], so there's an extension

[math]\displaystyle{ 0 \to \mathbb{Z}_2 \to \mathbb{Z}_4 \to \mathbb{Z}_2 \to 0 }[/math]

If the extension was split, then the group [math]\displaystyle{ G }[/math] in

[math]\displaystyle{ 0 \to \mathbb{Z}_2 \to G \to \mathbb{Z}_2 \to 0 }[/math]

would be isomorphic to [math]\displaystyle{ \mathbb{Z}_2\times\mathbb{Z}_2 }[/math].

Q₈

The group of the eight quaternions [math]\displaystyle{ \{\pm 1,\pm i,\pm j,\pm k\} }[/math] where [math]\displaystyle{ ijk = -1 }[/math] and [math]\displaystyle{ i^2 = j^2 = k^2 = -1 }[/math], is another example of a group^[6] which has non-trivial subgroups yet is still not split. For example, the subgroup generated by [math]\displaystyle{ i }[/math] is isomorphic to [math]\displaystyle{ \mathbb{Z}_4 }[/math] and is normal. It also has a subgroup of order [math]\displaystyle{ 2 }[/math] generated by [math]\displaystyle{ -1 }[/math]. This would mean [math]\displaystyle{ Q_8 }[/math] would have to be a split extension in the following hypothetical exact sequence of groups:

[math]\displaystyle{ 0 \to \mathbb{Z}_4 \to Q_8 \to \mathbb{Z}_2 \to 0 }[/math],

but such an exact sequence does not exist. This can be shown by computing the first group cohomology group of [math]\displaystyle{ \mathbb{Z}_2 }[/math] with coefficients in [math]\displaystyle{ \mathbb{Z}_4 }[/math], so [math]\displaystyle{ H^1(\mathbb{Z}_2,\mathbb{Z}_4) \cong \mathbb{Z}/2 }[/math] and noting the two groups in these extensions are [math]\displaystyle{ \mathbb{Z}_2\times\mathbb{Z}_4 }[/math] and the dihedral group [math]\displaystyle{ D_8 }[/math]. But, as neither of these groups is isomorphic with [math]\displaystyle{ Q_8 }[/math], the quaternion group is not split. This non-existence of isomorphisms can be checked by noting the trivial extension is abelian while [math]\displaystyle{ Q_8 }[/math] is non-abelian, and noting the only normal subgroups are [math]\displaystyle{ \mathbb{Z}_2 }[/math] and [math]\displaystyle{ \mathbb{Z}_4 }[/math], but [math]\displaystyle{ Q_8 }[/math] has three subgroups isomorphic to [math]\displaystyle{ \mathbb{Z}_4 }[/math].

Properties

If $G$ is the semidirect product of the normal subgroup $N$ and the subgroup $H$ , and both $N$ and $H$ are finite, then the order of $G$ equals the product of the orders of $N$ and $H$ . This follows from the fact that $G$ is of the same order as the outer semidirect product of $N$ and $H$ , whose underlying set is the Cartesian product $N \times H$ .

Relation to direct products

Suppose $G$ is a semidirect product of the normal subgroup $N$ and the subgroup $H$ . If $H$ is also normal in $G$ , or equivalently, if there exists a homomorphism $G \to N$ that is the identity on $N$ with kernel $H$ , then $G$ is the direct product of $N$ and $H$ .

The direct product of two groups $N$ and $H$ can be thought of as the semidirect product of $N$ and $H$ with respect to $φ (h) = id N$ for all $h$ in $H$ .

Note that in a direct product, the order of the factors is not important, since $N \times H$ is isomorphic to $H \times N$ . This is not the case for semidirect products, as the two factors play different roles.

Furthermore, the result of a (proper) semidirect product by means of a non-trivial homomorphism is never an abelian group, even if the factor groups are abelian.

Non-uniqueness of semidirect products (and further examples)

As opposed to the case with the direct product, a semidirect product of two groups is not, in general, unique; if $G$ and $G'$ are two groups that both contain isomorphic copies of $N$ as a normal subgroup and $H$ as a subgroup, and both are a semidirect product of $N$ and $H$ , then it does not follow that $G$ and $G'$ are isomorphic because the semidirect product also depends on the choice of an action of $H$ on $N$ .

For example, there are four non-isomorphic groups of order 16 that are semidirect products of $C 8$ and $C 2$ ; in this case, $C 8$ is necessarily a normal subgroup because it has index 2. One of these four semidirect products is the direct product, while the other three are non-abelian groups:

the dihedral group of order 16
the quasidihedral group of order 16
the Iwasawa group of order 16

If a given group is a semidirect product, then there is no guarantee that this decomposition is unique. For example, there is a group of order 24 (the only one containing six elements of order 4 and six elements of order 6) that can be expressed as semidirect product in the following ways: $(D 8 ⋉ C 3) ≅ (C 2 ⋉ Q 12) ≅ (C 2 ⋉ D 12) ≅ (D 6 ⋉ V)$ .^[7]

Existence

Main page: Schur–Zassenhaus theorem

In general, there is no known characterization (i.e., a necessary and sufficient condition) for the existence of semidirect products in groups. However, some sufficient conditions are known, which guarantee existence in certain cases. For finite groups, the Schur–Zassenhaus theorem guarantees existence of a semidirect product when the order of the normal subgroup is coprime to the order of the quotient group.

For example, the Schur–Zassenhaus theorem implies the existence of a semi-direct product among groups of order 6; there are two such products, one of which is a direct product, and the other a dihedral group. In contrast, the Schur–Zassenhaus theorem does not say anything about groups of order 4 or groups of order 8 for instance.

Generalizations

Within group theory, the construction of semidirect products can be pushed much further. The Zappa–Szep product of groups is a generalization that, in its internal version, does not assume that either subgroup is normal.

There is also a construction in ring theory, the crossed product of rings. This is constructed in the natural way from the group ring for a semidirect product of groups. The ring-theoretic approach can be further generalized to the semidirect sum of Lie algebras.

For geometry, there is also a crossed product for group actions on a topological space; unfortunately, it is in general non-commutative even if the group is abelian. In this context, the semidirect product is the space of orbits of the group action. The latter approach has been championed by Alain Connes as a substitute for approaches by conventional topological techniques; c.f. noncommutative geometry.

There are also far-reaching generalisations in category theory. They show how to construct fibred categories from indexed categories. This is an abstract form of the outer semidirect product construction.

Groupoids

Another generalization is for groupoids. This occurs in topology because if a group $G$ acts on a space $X$ it also acts on the fundamental groupoid $π 1 (X)$ of the space. The semidirect product $π 1 (X) ⋊ G$ is then relevant to finding the fundamental groupoid of the orbit space $X/G$ . For full details see Chapter 11 of the book referenced below, and also some details in semidirect product^[8] in ncatlab.

Abelian categories

Non-trivial semidirect products do not arise in abelian categories, such as the category of modules. In this case, the splitting lemma shows that every semidirect product is a direct product. Thus the existence of semidirect products reflects a failure of the category to be abelian.

Notation

Usually the semidirect product of a group $H$ acting on a group $N$ (in most cases by conjugation as subgroups of a common group) is denoted by $N ⋊ H$ or $H ⋉ N$ . However, some sources^[9] may use this symbol with the opposite meaning. In case the action $φ : H \to Aut(N)$ should be made explicit, one also writes $N ⋊ φ H$ . One way of thinking about the $N ⋊ H$ symbol is as a combination of the symbol for normal subgroup ( $◁$ ) and the symbol for the product ( $\times$ ). Barry Simon, in his book on group representation theory,^[10] employs the unusual notation [math]\displaystyle{ N\mathbin{\circledS_{\varphi}}H }[/math] for the semidirect product.

Unicode lists four variants:^[11]

	Value	MathML	Unicode description
⋉	U+22C9	ltimes	LEFT NORMAL FACTOR SEMIDIRECT PRODUCT
⋊	U+22CA	rtimes	RIGHT NORMAL FACTOR SEMIDIRECT PRODUCT
⋋	U+22CB	lthree	LEFT SEMIDIRECT PRODUCT
⋌	U+22CC	rthree	RIGHT SEMIDIRECT PRODUCT

Here the Unicode description of the rtimes symbol says "right normal factor", in contrast to its usual meaning in mathematical practice.

In LaTeX, the commands \rtimes and \ltimes produce the corresponding characters. With the AMS symbols package loaded, \leftthreetimes produces ⋋ and \rightthreetimes produces ⋌.

Notes

↑ DS Dummit and RM Foote (1991), Abstract algebra, Englewood Cliffs, NJ: Prentice Hall, 142.
↑ Robinson, Derek John Scott (2003). An Introduction to Abstract Algebra. Walter de Gruyter. pp. 75–76. ISBN 9783110175448.
↑ ^3.0 ^3.1 ^3.2 Mac Lane, Saunders; Birkhoff, Garrett (1999). Algebra (3rd ed.). American Mathematical Society. pp. 414–415. ISBN 0-8218-1646-2.
↑ Milne. Algebraic Groups. pp. 45, semi-direct products. https://www.jmilne.org/math/CourseNotes/iAG200.pdf.
↑ Thompson, Nick. "Irreducible Brillouin Zones and Band Structures". https://bandgap.io/blog/brillouin_zones/.
↑ "abstract algebra - Can every non-simple group $G$ be written as a semidirect product?". https://math.stackexchange.com/questions/1504422/can-every-non-simple-group-g-be-written-as-a-semidirect-product.
↑ H.E. Rose (2009). A Course on Finite Groups. Springer Science & Business Media. p. 183. ISBN 978-1-84882-889-6. Note that Rose uses the opposite notation convention than the one adopted on this page (p. 152).
↑ "Ncatlab.org". http://ncatlab.org/nlab/show/semidirect+product.
↑ e.g., E. B. Vinberg (2003). A Course in Algebra. Providence, RI: American Mathematical Society. p. 389. ISBN 0-8218-3413-4.
↑ B. Simon (1996). Representations of Finite and Compact Groups. Providence, RI: American Mathematical Society. p. 6. ISBN 0-8218-0453-7.
↑ See unicode.org

References

R. Brown, Topology and groupoids, Booksurge 2006. ISBN 1-4196-2722-8

0.00

(0 votes)

[1] DS Dummit and RM Foote (1991), Abstract algebra, Englewood Cliffs, NJ: Prentice Hall, 142.

[2] Robinson, Derek John Scott (2003). An Introduction to Abstract Algebra. Walter de Gruyter. pp. 75–76. ISBN 9783110175448.

[mac-lane-3] 3.0 ^3.1 ^3.2 Mac Lane, Saunders; Birkhoff, Garrett (1999). Algebra (3rd ed.). American Mathematical Society. pp. 414–415. ISBN 0-8218-1646-2.

[4] Milne. Algebraic Groups. pp. 45, semi-direct products. https://www.jmilne.org/math/CourseNotes/iAG200.pdf.

[5] Thompson, Nick. "Irreducible Brillouin Zones and Band Structures". https://bandgap.io/blog/brillouin_zones/.

[6] "abstract algebra - Can every non-simple group $G$ be written as a semidirect product?". https://math.stackexchange.com/questions/1504422/can-every-non-simple-group-g-be-written-as-a-semidirect-product.

[Rose2009-7] H.E. Rose (2009). A Course on Finite Groups. Springer Science & Business Media. p. 183. ISBN 978-1-84882-889-6. Note that Rose uses the opposite notation convention than the one adopted on this page (p. 152).

[8] "Ncatlab.org". http://ncatlab.org/nlab/show/semidirect+product.

[Vinberg(2003)-9] .g., E. B. Vinberg (2003). A Course in Algebra. Providence, RI: American Mathematical Society. p. 389. ISBN 0-8218-3413-4.

[Simon1996-10] B. Simon (1996). Representations of Finite and Compact Groups. Providence, RI: American Mathematical Society. p. 6. ISBN 0-8218-0453-7.

[11] See unicode.org

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Anonymous

Search

Semidirect product

Namespaces

More

Page actions

Contents

Inner semidirect product definitions

Inner and outer semidirect products

Examples

Dihedral group

Cyclic groups

Holomorph of a group

Fundamental group of the Klein bottle

Upper triangular matrices

Group of isometries on the plane

Orthogonal group O(n)

Semi-linear transformations

Crystallographic groups

Non-examples

Z₄

Q₈

Properties

Relation to direct products

Non-uniqueness of semidirect products (and further examples)

Existence

Generalizations

Groupoids

Abelian categories

Notation

See also

Notes

References

Navigation

Navigation

Help

Translate

Wiki tools

Wiki tools

Anonymous

Search

Semidirect product

Inner semidirect product definitions

Inner and outer semidirect products

Examples

Dihedral group

Cyclic groups

Holomorph of a group

Fundamental group of the Klein bottle

Upper triangular matrices

Group of isometries on the plane

Orthogonal group O(n)

Semi-linear transformations

Crystallographic groups

Non-examples

Z4

Q8

Properties

Relation to direct products

Non-uniqueness of semidirect products (and further examples)

Existence

Generalizations

Groupoids

Abelian categories

Notation

See also

Notes

References

Navigation

Wiki tools

Page tools

Other projects

Categories

Z₄

Q₈