Hyperbolic group

From HandWiki
Short description: Mathematical concept
Algebraic structure → Group theory
Group theory
Cyclic group.svg
Basic notions
Group homomorphisms
Finite groups
Classification of finite simple groups
Modular groups
  • PSL(2,Z)
  • SL(2,Z)
Topological and Lie groups
Infinite dimensional Lie group
  • O(∞)
  • SU(∞)
  • Sp(∞)
Algebraic groups

In group theory, more precisely in geometric group theory, a hyperbolic group, also known as a word hyperbolic group or Gromov hyperbolic group, is a finitely generated group equipped with a word metric satisfying certain properties abstracted from classical hyperbolic geometry. The notion of a hyperbolic group was introduced and developed by Mikhail Gromov (1987). The inspiration came from various existing mathematical theories: hyperbolic geometry but also low-dimensional topology (in particular the results of Max Dehn concerning the fundamental group of a hyperbolic Riemann surface, and more complex phenomena in three-dimensional topology), and combinatorial group theory. In a very influential (over 1000 citations [1]) chapter from 1987, Gromov proposed a wide-ranging research program. Ideas and foundational material in the theory of hyperbolic groups also stem from the work of George Mostow, William Thurston, James W. Cannon, Eliyahu Rips, and many others.

Definition

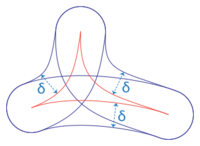
Let [math]\displaystyle{ G }[/math] be a finitely generated group, and [math]\displaystyle{ X }[/math] be its Cayley graph with respect to some finite set [math]\displaystyle{ S }[/math] of generators. The set [math]\displaystyle{ X }[/math] is endowed with its graph metric (in which edges are of length one and the distance between two vertices is the minimal number of edges in a path connecting them) which turns it into a length space. The group [math]\displaystyle{ G }[/math] is then said to be hyperbolic if [math]\displaystyle{ X }[/math] is a hyperbolic space in the sense of Gromov. Shortly, this means that there exists a [math]\displaystyle{ \delta \gt 0 }[/math] such that any geodesic triangle in [math]\displaystyle{ X }[/math] is [math]\displaystyle{ \delta }[/math]-thin, as illustrated in the figure on the right (the space is then said to be [math]\displaystyle{ \delta }[/math]-hyperbolic).

[math]\displaystyle{ x }[/math]
[math]\displaystyle{ y }[/math]
[math]\displaystyle{ z }[/math]
[math]\displaystyle{ B_\delta([x,y]) }[/math]
[math]\displaystyle{ B_\delta([z,x]) }[/math]
[math]\displaystyle{ B_\delta([y,z]) }[/math]
The δ-thin triangle condition

A priori this definition depends on the choice of a finite generating set [math]\displaystyle{ S }[/math]. That this is not the case follows from the two following facts:

  • the Cayley graphs corresponding to two finite generating sets are always quasi-isometric one to the other;
  • any geodesic space which is quasi-isometric to a geodesic Gromov-hyperbolic space is itself Gromov-hyperbolic.

Thus we can legitimately speak of a finitely generated group [math]\displaystyle{ G }[/math] being hyperbolic without referring to a generating set. On the other hand, a space which is quasi-isometric to a [math]\displaystyle{ \delta }[/math]-hyperbolic space is itself [math]\displaystyle{ \delta' }[/math]-hyperbolic for some [math]\displaystyle{ \delta' \gt 0 }[/math] but the latter depends on both the original [math]\displaystyle{ \delta }[/math] and on the quasi-isometry, thus it does not make sense to speak of [math]\displaystyle{ G }[/math] being [math]\displaystyle{ \delta }[/math]-hyperbolic.

Remarks

The Švarc–Milnor lemma[2] states that if a group [math]\displaystyle{ G }[/math] acts properly discontinuously and with compact quotient (such an action is often called geometric) on a proper length space [math]\displaystyle{ Y }[/math], then it is finitely generated, and any Cayley graph for [math]\displaystyle{ G }[/math] is quasi-isometric to [math]\displaystyle{ Y }[/math]. Thus a group is (finitely generated and) hyperbolic if and only if it has a geometric action on a proper hyperbolic space.

If [math]\displaystyle{ G' \subset G }[/math] is a subgroup with finite index (i.e., the set [math]\displaystyle{ G/G' }[/math] is finite), then the inclusion induces a quasi-isometry on the vertices of any locally finite Cayley graph of [math]\displaystyle{ G' }[/math] into any locally finite Cayley graph of [math]\displaystyle{ G }[/math]. Thus [math]\displaystyle{ G' }[/math] is hyperbolic if and only if [math]\displaystyle{ G }[/math] itself is. More generally, if two groups are commensurable, then one is hyperbolic if and only if the other is.

Examples

Elementary hyperbolic groups

The simplest examples of hyperbolic groups are finite groups (whose Cayley graphs are of finite diameter, hence [math]\displaystyle{ \delta }[/math]-hyperbolic with [math]\displaystyle{ \delta }[/math] equal to this diameter).

Another simple example is given by the infinite cyclic group [math]\displaystyle{ \Z }[/math]: the Cayley graph of [math]\displaystyle{ \Z }[/math] with respect to the generating set [math]\displaystyle{ \{ \pm 1 \} }[/math] is a line, so all triangles are line segments and the graph is [math]\displaystyle{ 0 }[/math]-hyperbolic. It follows that any group which is virtually cyclic (contains a copy of [math]\displaystyle{ \Z }[/math] of finite index) is also hyperbolic, for example the infinite dihedral group.

Members in this class of groups are often called elementary hyperbolic groups (the terminology is adapted from that of actions on the hyperbolic plane).

Free groups and groups acting on trees

Let [math]\displaystyle{ S = \{a_1, \ldots, a_n\} }[/math] be a finite set and [math]\displaystyle{ F }[/math] be the free group with generating set [math]\displaystyle{ S }[/math]. Then the Cayley graph of [math]\displaystyle{ F }[/math] with respect to [math]\displaystyle{ S }[/math] is a locally finite tree and hence a 0-hyperbolic space. Thus [math]\displaystyle{ F }[/math] is a hyperbolic group.

More generally we see that any group [math]\displaystyle{ G }[/math] which acts properly discontinuously on a locally finite tree (in this context this means exactly that the stabilizers in [math]\displaystyle{ G }[/math] of the vertices are finite) is hyperbolic. Indeed, this follows from the fact that [math]\displaystyle{ G }[/math] has an invariant subtree on which it acts with compact quotient, and the Svarc—Milnor lemma. Such groups are in fact virtually free (i.e. contain a finitely generated free subgroup of finite index), which gives another proof of their hyperbolicity.

An interesting example is the modular group [math]\displaystyle{ G = \mathrm{SL}_2(\mathbb Z) }[/math]: it acts on the tree given by the 1-skeleton of the associated tessellation of the hyperbolic plane and it has a finite index free subgroup (on two generators) of index 6 (for example the set of matrices in [math]\displaystyle{ G }[/math] which reduce to the identity modulo 2 is such a group). Note an interesting feature of this example: it acts properly discontinuously on a hyperbolic space (the hyperbolic plane) but the action is not cocompact (and indeed [math]\displaystyle{ G }[/math] is not quasi-isometric to the hyperbolic plane).

Fuchsian groups

Generalising the example of the modular group a Fuchsian group is a group admitting a properly discontinuous action on the hyperbolic plane (equivalently, a discrete subgroup of [math]\displaystyle{ \mathrm{SL}_2(\mathbb R) }[/math]). The hyperbolic plane is a [math]\displaystyle{ \delta }[/math]-hyperbolic space and hence the Svarc—Milnor lemma tells us that cocompact Fuchsian groups are hyperbolic.

Examples of such are the fundamental groups of closed surfaces of negative Euler characteristic. Indeed, these surfaces can be obtained as quotients of the hyperbolic plane, as implied by the Poincaré—Koebe Uniformisation theorem.

Another family of examples of cocompact Fuchsian groups is given by triangle groups: all but finitely many are hyperbolic.

Negative curvature

Generalising the example of closed surfaces, the fundamental groups of compact Riemannian manifolds with strictly negative sectional curvature are hyperbolic. For example, cocompact lattices in the orthogonal or unitary group preserving a form of signature [math]\displaystyle{ (n,1) }[/math] are hyperbolic.

A further generalisation is given by groups admitting a geometric action on a CAT(k) space, when [math]\displaystyle{ k }[/math] is any negative number.[3] There exist examples which are not commensurable to any of the previous constructions (for instance groups acting geometrically on hyperbolic buildings).

Small cancellation groups

Groups having presentations which satisfy small cancellation conditions are hyperbolic. This gives a source of examples which do not have a geometric origin as the ones given above. In fact one of the motivations for the initial development of hyperbolic groups was to give a more geometric interpretation of small cancellation.

Random groups

In some sense, "most" finitely presented groups with large defining relations are hyperbolic. For a quantitative statement of what this means see Random group.

Non-examples

  • The simplest example of a group which is not hyperbolic is the free rank 2 abelian group [math]\displaystyle{ \mathbb Z^2 }[/math]. Indeed, it is quasi-isometric to the Euclidean plane which is easily seen not to be hyperbolic (for example because of the existence of homotheties).
  • More generally, any group which contains [math]\displaystyle{ \Z^2 }[/math] as a subgroup is not hyperbolic.[4][5] In particular, lattices in higher rank semisimple Lie groups and the fundamental groups [math]\displaystyle{ \pi_1(S^3\setminus K) }[/math] of nontrivial knot complements fall into this category and therefore are not hyperbolic. This is also the case for mapping class groups of closed hyperbolic surfaces.
  • The Baumslag–Solitar groups B(m,n) and any group that contains a subgroup isomorphic to some B(m,n) fail to be hyperbolic (since B(1,1) = [math]\displaystyle{ \Z^2 }[/math], this generalizes the previous example).
  • A non-uniform lattice in a rank 1 simple Lie group is hyperbolic if and only if the group is isogenous to [math]\displaystyle{ \mathrm{SL}_2(\R) }[/math] (equivalently the associated symmetric space is the hyperbolic plane). An example of this is given by hyperbolic knot groups. Another is the Bianchi groups, for example [math]\displaystyle{ \mathrm{SL}_2(\sqrt{-1}) }[/math].

Properties

Algebraic properties

  • Hyperbolic groups satisfy the Tits alternative: they are either virtually solvable (this possibility is satisfied only by elementary hyperbolic groups) or they have a subgroup isomorphic to a nonabelian free group.
  • Non-elementary hyperbolic groups are not simple in a very strong sense: if [math]\displaystyle{ G }[/math] is non-elementary hyperbolic then there exists an infinite subgroup [math]\displaystyle{ H \triangleleft G }[/math] such that [math]\displaystyle{ H }[/math] and [math]\displaystyle{ G/H }[/math] are both infinite.
  • It is not known whether there exists a hyperbolic group which is not residually finite.

Geometric properties

  • Non-elementary (infinite and not virtually cyclic) hyperbolic groups have always exponential growth rate (this is a consequence of the Tits alternative).
  • Hyperbolic groups satisfy a linear isoperimetric inequality.[6]

Homological properties

  • Hyperbolic groups are always finitely presented. In fact one can explicitly construct a complex (the Rips complex) which is contractible and on which the group acts geometrically[7] so it is of type F∞. When the group is torsion-free the action is free, showing that the group has finite cohomological dimension.
  • In 2002, I. Mineyev showed that hyperbolic groups are exactly those finitely generated groups for which the comparison map between the bounded cohomology and ordinary cohomology is surjective in all degrees, or equivalently, in degree 2.[8]

Algorithmic properties

  • Hyperbolic groups have a solvable word problem. They are biautomatic and automatic.[9] Indeed, they are strongly geodesically automatic, that is, there is an automatic structure on the group, where the language accepted by the word acceptor is the set of all geodesic words.
  • It was shown in 2010 that hyperbolic groups have a decidable marked isomorphism problem.[10] It is notable that this means that the isomorphism problem, orbit problems (in particular the conjugacy problem) and Whitehead's problem are all decidable.
  • Cannon and Swenson have shown that hyperbolic groups with a 2-sphere at infinity have a natural subdivision rule.[11] This is related to Cannon's conjecture.

Generalisations

Relatively hyperbolic groups

Relatively hyperbolic groups are a class generalising hyperbolic groups. Very roughly[12] [math]\displaystyle{ G }[/math] is hyperbolic relative to a collection [math]\displaystyle{ \mathcal G }[/math] of subgroups if it admits a (not necessarily cocompact) properly discontinuous action on a proper hyperbolic space [math]\displaystyle{ X }[/math] which is "nice" on the boundary of [math]\displaystyle{ X }[/math] and such that the stabilisers in [math]\displaystyle{ G }[/math] of points on the boundary are subgroups in [math]\displaystyle{ \mathcal G }[/math]. This is interesting when both [math]\displaystyle{ X }[/math] and the action of [math]\displaystyle{ G }[/math] on [math]\displaystyle{ X }[/math] are not elementary (in particular [math]\displaystyle{ X }[/math] is infinite: for example every group is hyperbolic relatively to itself via its action on a single point!).

Interesting examples in this class include in particular non-uniform lattices in rank 1 semisimple Lie groups, for example fundamental groups of non-compact hyperbolic manifolds of finite volume. Non-examples are lattices in higher-rank Lie groups and mapping class groups.

Acylindrically hyperbolic groups

An even more general notion is that of an acylindically hyperbolic group.[13] Acylindricity of an action of a group [math]\displaystyle{ G }[/math] on a metric space [math]\displaystyle{ X }[/math] is a weakening of proper discontinuity of the action.[14]

A group is said to be acylindrically hyperbolic if it admits a non-elementary acylindrical action on a (not necessarily proper) Gromov-hyperbolic space. This notion includes mapping class groups via their actions on curve complexes. Lattices in higher-rank Lie groups are (still!) not acylindrically hyperbolic.

CAT(0) groups

In another direction one can weaken the assumption about curvature in the examples above: a CAT(0) group is a group admitting a geometric action on a CAT(0) space. This includes Euclidean crystallographic groups and uniform lattices in higher-rank Lie groups.

It is not known whether there exists a hyperbolic group which is not CAT(0).[15]

Notes

  1. ↑ Gromov, Mikhail (1987). "Hyperbolic Groups". in Gersten, S.M.. Essays in Group Theory. Mathematical Sciences Research Institute Publications, vol 8.. New York, NY: Springer. pp. 75–263. https://www.ams.org/mathscinet-getitem?mr=919829. 
  2. ↑ Bowditch 2006, Theorem 3.6.
  3. ↑ for a proof that this includes the previous examples see https://lamington.wordpress.com/2012/10/17/upper-curvature-bounds-and-catk/
  4. ↑ Ghys & de la Harpe 1990, Ch. 8, Th. 37.
  5. ↑ Bridson & Haefliger 1999, Chapter 3.Γ, Corollary 3.10..
  6. ↑ Bowditch 2006, (F4) in paragraph 6.11.2.
  7. ↑ Ghys & de la Harpe 1990, Chapitre 4.
  8. ↑ Mineyev 2002.
  9. ↑ Charney 1992.
  10. ↑ Dahmani & Guirardel 2011.
  11. ↑ Cannon & Swenson 1998.
  12. ↑ Bowditch 2012.
  13. ↑ Osin 2016.
  14. ↑ In some detail: it asks that for every [math]\displaystyle{ \varepsilon \gt 0 }[/math] there exist [math]\displaystyle{ R, N \gt 0 }[/math] such that for every two points [math]\displaystyle{ x, y \in X }[/math] which are at least [math]\displaystyle{ R }[/math] apart there are at most [math]\displaystyle{ N }[/math] elements [math]\displaystyle{ g \in G }[/math] satisfying [math]\displaystyle{ d(x, gx) \lt \varepsilon }[/math] and [math]\displaystyle{ d(y, gy) \lt \varepsilon }[/math].
  15. ↑ "Are all δ-hyperbolic groups CAT(0)?". Stack Exchange. February 10, 2015. https://math.stackexchange.com/q/1141526. 

References

  • Bridson, Martin R.; Haefliger, André (1999). Metric spaces of non-positive curvature. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 319. Berlin: Springer-Verlag. doi:10.1007/978-3-662-12494-9. ISBN 3-540-64324-9. 

Further reading



Retrieved from "https://handwiki.org/wiki/index.php?title=Hyperbolic_group&oldid=3372499"