Lorentz group
| Algebraic structure → Group theory Group theory |
|---|
 |

In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicist Hendrik Lorentz.
For example, the following laws, equations, and theories respect Lorentz symmetry:
- The kinematical laws of special relativity
- Maxwell's field equations in the theory of electromagnetism
- The Dirac equation in the theory of the electron
- The Standard Model of particle physics
The Lorentz group expresses the fundamental symmetry of space and time of all known fundamental laws of nature. In small enough regions of spacetime where gravitational variances are negligible, physical laws are Lorentz invariant in the same manner as special relativity.
Basic properties
The Lorentz group is a subgroup of the Poincaré group—the group of all isometries of Minkowski spacetime. Lorentz transformations are, precisely, isometries that leave the origin fixed. Thus, the Lorentz group is the isotropy subgroup with respect to the origin of the isometry group of Minkowski spacetime. For this reason, the Lorentz group is sometimes called the homogeneous Lorentz group while the Poincaré group is sometimes called the inhomogeneous Lorentz group. Lorentz transformations are examples of linear transformations; general isometries of Minkowski spacetime are affine transformations.
Physics definition
Assume two inertial reference frames (t, x, y, z) and (t′, x′, y′, z′), and two points P1, P2, the Lorentz group is the set of all the transformations between the two reference frames that preserve the speed of light propagating between the two points:
- [math]\displaystyle{ c^2(\Delta t')^2 - (\Delta x')^2 - (\Delta y')^2 - (\Delta z')^2 = c^2(\Delta t)^2 - (\Delta x)^2 - (\Delta y)^2 - (\Delta z)^2 }[/math]
In matrix form these are all the linear transformations Λ such that:
- [math]\displaystyle{ \Lambda^\textsf{T} \eta \Lambda = \eta\qquad\eta = \operatorname{diag}(1,-1,-1,-1) }[/math]
These are then called Lorentz transformations
Mathematical definition
Mathematically, the Lorentz group may be described as the indefinite orthogonal group O(1, 3), the matrix Lie group that preserves the quadratic form
- [math]\displaystyle{ (t, x, y, z) \mapsto t^2 - x^2 - y^2 - z^2 }[/math]
on R4 (the vector space equipped with this quadratic form is sometimes written R1,3). This quadratic form is, when put on matrix form (see Classical orthogonal group), interpreted in physics as the metric tensor of Minkowski spacetime.
Mathematical properties
The Lorentz group is a six-dimensional noncompact non-abelian real Lie group that is not connected. The four connected components are not simply connected.[1] The identity component (i.e., the component containing the identity element) of the Lorentz group is itself a group, and is often called the restricted Lorentz group, and is denoted SO+(1, 3). The restricted Lorentz group consists of those Lorentz transformations that preserve both the orientation of space and the direction of time. Its fundamental group has order 2, and its universal cover, the indefinite spin group Spin(1, 3), is isomorphic to both the special linear group SL(2, C) and to the symplectic group Sp(2, C). These isomorphisms allow the Lorentz group to act on a large number of mathematical structures important to physics, most notably spinors. Thus, in relativistic quantum mechanics and in quantum field theory, it is very common to call SL(2, C) the Lorentz group, with the understanding that SO+(1, 3) is a specific representation (the vector representation) of it.
A recurrent representation of the action of the Lorentz group on Minkowski space uses biquaternions, which form a composition algebra. The isometry property of Lorentz transformations holds according to the composition property [math]\displaystyle{ | p q | = | p | \times | q | }[/math].
Another property of the Lorentz group is conformality or preservation of angles. Lorentz boosts act by hyperbolic rotation of a spacetime plane, and such "rotations" preserve hyperbolic angle, the measure of rapidity used in relativity. Therefore the Lorentz group is a subgroup of the conformal group of spacetime.
Note that this article refers to O(1, 3) as the "Lorentz group", SO(1, 3) as the "proper Lorentz group", and SO+(1, 3) as the "restricted Lorentz group". Many authors (especially in physics) use the name "Lorentz group" for SO(1, 3) (or sometimes even SO+(1, 3)) rather than O(1, 3). When reading such authors it is important to keep clear exactly which they are referring to.
Connected components
Because it is a Lie group, the Lorentz group O(1, 3) is a group and also has a topological description as a smooth manifold. As a manifold, it has four connected components. Intuitively, this means that it consists of four topologically separated pieces.
The four connected components can be categorized by two transformation properties its elements have:
- Some elements are reversed under time-inverting Lorentz transformations, for example, a future-pointing timelike vector would be inverted to a past-pointing vector
- Some elements have orientation reversed by improper Lorentz transformations, for example, certain vierbein (tetrads)
Lorentz transformations that preserve the direction of time are called orthochronous. The subgroup of orthochronous transformations is often denoted O+(1, 3). Those that preserve orientation are called proper, and as linear transformations they have determinant +1. (The improper Lorentz transformations have determinant −1.) The subgroup of proper Lorentz transformations is denoted SO(1, 3).
The subgroup of all Lorentz transformations preserving both orientation and direction of time is called the proper, orthochronous Lorentz group or restricted Lorentz group, and is denoted by SO+(1, 3).[lower-alpha 1]
The set of the four connected components can be given a group structure as the quotient group O(1, 3) / SO+(1, 3), which is isomorphic to the Klein four-group. Every element in O(1, 3) can be written as the semidirect product of a proper, orthochronous transformation and an element of the discrete group
- {1, P, T, PT}
where P and T are the parity and time reversal operators:
- P = diag(1, −1, −1, −1)
- T = diag(−1, 1, 1, 1).
Thus an arbitrary Lorentz transformation can be specified as a proper, orthochronous Lorentz transformation along with a further two bits of information, which pick out one of the four connected components. This pattern is typical of finite-dimensional Lie groups.
Restricted Lorentz group
The restricted Lorentz group SO+(1, 3) is the identity component of the Lorentz group, which means that it consists of all Lorentz transformations that can be connected to the identity by a continuous curve lying in the group. The restricted Lorentz group is a connected normal subgroup of the full Lorentz group with the same dimension, in this case with dimension six.
The restricted Lorentz group is generated by ordinary spatial rotations and Lorentz boosts (which are rotations in a hyperbolic space that includes a time-like direction[2]). Since every proper, orthochronous Lorentz transformation can be written as a product of a rotation (specified by 3 real parameters) and a boost (also specified by 3 real parameters), it takes 6 real parameters to specify an arbitrary proper orthochronous Lorentz transformation. This is one way to understand why the restricted Lorentz group is six-dimensional. (See also the Lie algebra of the Lorentz group.)
The set of all rotations forms a Lie subgroup isomorphic to the ordinary rotation group SO(3). The set of all boosts, however, does not form a subgroup, since composing two boosts does not, in general, result in another boost. (Rather, a pair of non-colinear boosts is equivalent to a boost and a rotation, and this relates to Thomas rotation.) A boost in some direction, or a rotation about some axis, generates a one-parameter subgroup.
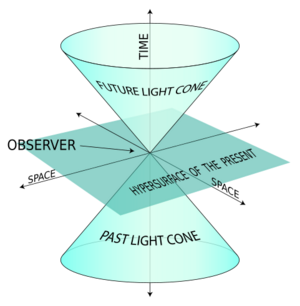
Surfaces of transitivity
If a group G acts on a space V, then a surface S ⊂ V is a surface of transitivity if S is invariant under G (i.e., ∀g ∈ G, ∀s ∈ S: gs ∈ S) and for any two points s1, s2 ∈ S there is a g ∈ G such that gs1 = s2. By definition of the Lorentz group, it preserves the quadratic form
- [math]\displaystyle{ Q(x) = x_0^2 - x_1^2 - x_2^2 - x_3^2. }[/math]
The surfaces of transitivity of the orthochronous Lorentz group O+(1, 3), Q(x) = const. acting on flat spacetime R1,3 are the following:[3]
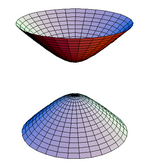
- Q(x) > 0, x0 > 0 is the upper branch of a hyperboloid of two sheets. Points on this sheet are separated from the origin by a future time-like vector.
- Q(x) > 0, x0 < 0 is the lower branch of this hyperboloid. Points on this sheet are the past time-like vectors.
- Q(x) = 0, x0 > 0 is the upper branch of the light cone, the future light cone.
- Q(x) = 0, x0 < 0 is the lower branch of the light cone, the past light cone.
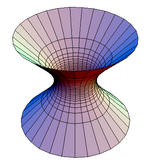
- Q(x) < 0 is a hyperboloid of one sheet. Points on this sheet are space-like separated from the origin.
- The origin x0 = x1 = x2 = x3 = 0.
These surfaces are 3-dimensional, so the images are not faithful, but they are faithful for the corresponding facts about O+(1, 2). For the full Lorentz group, the surfaces of transitivity are only four since the transformation T takes an upper branch of a hyperboloid (cone) to a lower one and vice versa.
As symmetric spaces
An equivalent way to formulate the above surfaces of transitivity is as a symmetric space in the sense of Lie theory. For example, the upper sheet of the hyperboloid can be written as the quotient space SO+(1, 3) / SO(3), due to the orbit-stabilizer theorem. Furthermore, this upper sheet also provides a model for three-dimensional hyperbolic space.
Representations of the Lorentz group
These observations constitute a good starting point for finding all infinite-dimensional unitary representations of the Lorentz group, in fact, of the Poincaré group, using the method of induced representations.[4] One begins with a "standard vector", one for each surface of transitivity, and then ask which subgroup preserves these vectors. These subgroups are called little groups by physicists. The problem is then essentially reduced to the easier problem of finding representations of the little groups. For example, a standard vector in one of the hyperbolas of two sheets could be suitably chosen as (m, 0, 0, 0). For each m ≠ 0, the vector pierces exactly one sheet. In this case the little group is SO(3), the rotation group, all of whose representations are known. The precise infinite-dimensional unitary representation under which a particle transforms is part of its classification. Not all representations can correspond to physical particles (as far as is known). Standard vectors on the one-sheeted hyperbolas would correspond to tachyons. Particles on the light cone are photons, and more hypothetically, gravitons. The "particle" corresponding to the origin is the vacuum.
Homomorphisms and isomorphisms
| Algebraic structure → Group theory Group theory |
|---|
 |
Several other groups are either homomorphic or isomorphic to the restricted Lorentz group SO+(1, 3). These homomorphisms play a key role in explaining various phenomena in physics.
- The special linear group SL(2, C) is a double covering of the restricted Lorentz group. This relationship is widely used to express the Lorentz invariance of the Dirac equation and the covariance of spinors. In other words, the (restricted) Lorentz group is isomorphic to SL(2, C) / Z2
- The symplectic group Sp(2, C) is isomorphic to SL(2, C); it is used to construct Weyl spinors, as well as to explain how spinors can have a mass.
- The spin group Spin(1, 3) is isomorphic to SL(2, C); it is used to explain spin and spinors in terms of the Clifford algebra, thus making it clear how to generalize the Lorentz group to general settings in Riemannian geometry, including theories of supergravity and string theory.
- The restricted Lorentz group is isomorphic to the projective special linear group PSL(2, C) which is, in turn, isomorphic to the Möbius group, the symmetry group of conformal geometry on the Riemann sphere. This relationship is central to the classification of the subgroups of the Lorentz group according to an earlier classification scheme developed for the Möbius group.
Weyl representation
The Weyl representation or spinor map is a pair of surjective homomorphisms from SL(2, C) to SO+(1, 3). They form a matched pair under parity transformations, corresponding to left and right chiral spinors.
One may define an action of SL(2, C) on Minkowski spacetime by writing a point of spacetime as a two-by-two Hermitian matrix in the form
- [math]\displaystyle{ \overline{X} = \begin{bmatrix} ct + z & x - iy \\ x + iy & ct - z \end{bmatrix} = ct 1\!\!1 + x\sigma_x + y\sigma_y + z\sigma_z = ct 1\!\!1 + \vec{x} \cdot \vec{\sigma} }[/math]
in terms of Pauli matrices.
This presentation, the Weyl presentation, satisfies
- [math]\displaystyle{ \det\, \overline{X} = (ct)^2 - x^2 - y^2 - z^2. }[/math]
Therefore, one has identified the space of Hermitian matrices (which is four-dimensional, as a real vector space) with Minkowski spacetime, in such a way that the determinant of a Hermitian matrix is the squared length of the corresponding vector in Minkowski spacetime. An element S ∈ SL(2, C) acts on the space of Hermitian matrices via
- [math]\displaystyle{ \overline{X} \mapsto S \overline{X} S^\dagger ~, }[/math]
where [math]\displaystyle{ S^\dagger }[/math] is the Hermitian transpose of S. This action preserves the determinant and so SL(2, C) acts on Minkowski spacetime by (linear) isometries. The parity-inverted form of the above is
- [math]\displaystyle{ X = ct 1\!\!1 - \vec{x} \cdot \vec{\sigma} }[/math]
which transforms as
- [math]\displaystyle{ X \mapsto \left(S^{-1}\right)^\dagger X S^{-1} }[/math]
That this is the correct transformation follows by noting that
- [math]\displaystyle{ \overline{X} X = \left(c^2 t^2 - \vec{x}\cdot\vec{x}\right) 1\!\!1 = \left(c^2 t^2 - x^2 - y^2 - z^2\right) 1\!\!1 }[/math]
remains invariant under the above pair of transformations.
These maps are surjective, and kernel of either map is the two element subgroup ±I. By the first isomorphism theorem, the quotient group PSL(2, C) = SL(2, C) / {±I} is isomorphic to SO+(1, 3).
The parity map swaps these two coverings. It corresponds to Hermitian conjugation being an automorphism of SL(2, C). These two distinct coverings corresponds to the two distinct chiral actions of the Lorentz group on spinors. The non-overlined form corresponds to right-handed spinors transforming as [math]\displaystyle{ \psi_R\mapsto S\psi_R }[/math], while the overline form corresponds to left-handed spinors transforming as [math]\displaystyle{ \psi_L\mapsto \left(S^\dagger\right)^{-1} \psi_L }[/math].[lower-alpha 2]
It is important to observe that this pair of coverings does not survive quantization; when quantized, this leads to the peculiar phenomenon of the chiral anomaly. The classical (i.e., non-quantized) symmetries of the Lorentz group are broken by quantization; this is the content of the Atiyah–Singer index theorem.
Notational conventions
In physics, it is conventional to denote a Lorentz transformation Λ ∈ SO+(1, 3) as [math]\displaystyle{ {\Lambda^\mu}_\nu }[/math], thus showing the matrix with spacetime indexes μ, ν = 0, 1, 2, 3. A four-vector can be created from the Pauli matrices in two different ways: as [math]\displaystyle{ \sigma^\mu = (I, \vec\sigma) }[/math] and as [math]\displaystyle{ {\overline\sigma}^\mu = \left(I, -\vec\sigma\right) }[/math]. The two forms are related by a parity transformation. Note that [math]\displaystyle{ {\overline\sigma}_\mu = \sigma^\mu }[/math].
Given a Lorentz transformation [math]\displaystyle{ x^\mu \mapsto x^{\prime\mu} = {\Lambda^\mu}_\nu x^\nu }[/math], the double-covering of the orthochronous Lorentz group by S ∈ SL(2, C) given above can be written as
- [math]\displaystyle{ x^{\prime\mu}{\overline\sigma}_\mu = {\overline\sigma}_\mu {\Lambda^\mu}_\nu x^\nu = S x^\nu {\overline\sigma}_\nu S^\dagger }[/math]
Dropping the [math]\displaystyle{ x^\mu }[/math] this takes the form
- [math]\displaystyle{ {\overline\sigma}_\mu {\Lambda^\mu}_\nu = S {\overline\sigma}_\nu S^\dagger }[/math]
The parity conjugate form is
- [math]\displaystyle{ \sigma_\mu {\Lambda^\mu}_\nu = \left(S^{-1}\right)^\dagger \sigma_\nu S^{-1} }[/math]
Proof
That the above is the correct form for indexed notation is not immediately obvious, partly because, when working in indexed notation, it is quite easy to accidentally confuse a Lorentz transform with its inverse, or its transpose. This confusion arises due to the identity [math]\displaystyle{ \eta\Lambda^\textsf{T}\eta = \Lambda^{-1} }[/math] being difficult to recognize when written in indexed form. Lorentz transforms are not tensors under Lorentz transformations! Thus a direct proof of this identity is useful, for establishing its correctness. It can be demonstrated by starting with the identity
- [math]\displaystyle{ \omega \sigma^k \omega^{-1} = -\left(\sigma^k\right)^\textsf{T} = -\left(\sigma^k\right)^* }[/math]
where [math]\displaystyle{ k = 1, 2, 3 }[/math] so that the above are just the usual Pauli matrices, and [math]\displaystyle{ (\cdot)^\textsf{T} }[/math] is the matrix transpose, and [math]\displaystyle{ (\cdot)^* }[/math] is complex conjugation. The matrix [math]\displaystyle{ \omega }[/math] is
- [math]\displaystyle{ \omega = i\sigma_2 = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} }[/math]
Written as the four-vector, the relationship is
- [math]\displaystyle{ \sigma^\textsf{T}_\mu = \sigma^*_\mu =\omega \overline{\sigma}_\mu \omega^{-1} }[/math]
This transforms as
- [math]\displaystyle{ \begin{align} \sigma^\textsf{T}_\mu {\Lambda^\mu}_\nu &= \omega \overline{\sigma}_\mu \omega^{-1} {\Lambda^\mu}_\nu \\ &= \omega S\; \overline{\sigma}_\nu\, S^\dagger \omega^{-1} \\ &= \left(\omega S \omega^{-1}\right)\, \left(\omega \overline{\sigma}_\nu \omega^{-1}\right)\, \left(\omega S^\dagger \omega^{-1}\right) \\ &= \left(S^{-1}\right)^\textsf{T}\, \sigma^\textsf{T}_\nu\, \left(S^{-1}\right)^* \end{align} }[/math]
Taking one more transpose, one gets
- [math]\displaystyle{ \sigma_\mu {\Lambda^\mu}_\nu = \left(S^{-1}\right)^\dagger \sigma_\nu S^{-1} }[/math]
Symplectic group
The symplectic group Sp(2, C) is isomorphic to SL(2, C). This isomorphism is constructed so as to preserve a symplectic bilinear form on C2, that is, to leave the form invariant under Lorentz transformations. This may be articulated as follows. The symplectic group is defined as
- [math]\displaystyle{ \operatorname{Sp}(2,\mathbf{C}) = \left\{S\in \operatorname{GL}(2,\mathbf{C}) : S^\textsf{T} \omega S=\omega \right\} }[/math]
where
- [math]\displaystyle{ \omega = i\sigma_2 = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} }[/math]
Other common notations are [math]\displaystyle{ \omega = \epsilon }[/math] for this element; sometimes J is used, but this invites confusion with the idea of almost complex structures, which are not the same, as they transform differently.
Given a pair of Weyl spinors (two-component spinors)
- [math]\displaystyle{ u = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} ~,\quad v = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} }[/math]
the invariant bilinear form is conventionally written as
- [math]\displaystyle{ \langle u,v\rangle = - \langle v, u\rangle = u_1 v_2 - u_2 v_1 = u^\textsf{T}\omega v }[/math]
This form is invariant under the Lorentz group, so that for S ∈ SL(2, C) one has
- [math]\displaystyle{ \langle Su, Sv\rangle = \langle u,v\rangle }[/math]
This defines a kind of "scalar product" of spinors, and is commonly used to defined a Lorentz-invariant mass term in Lagrangians. There are several notable properties to be called out that are important to physics. One is that [math]\displaystyle{ \omega^2 = -1 }[/math] and so [math]\displaystyle{ \omega^{-1} = \omega^\textsf{T} = \omega^\dagger = -\omega }[/math]
The defining relation can be written as
- [math]\displaystyle{ \omega S^\textsf{T} \omega^{-1} = S^{-1} }[/math]
which closely resembles the defining relation for the Lorentz group
- [math]\displaystyle{ \eta \Lambda^\textsf{T} \eta^{-1} = \Lambda^{-1} }[/math]
where [math]\displaystyle{ \eta = \operatorname{diag} (+1, -1, -1, -1) }[/math] is the metric tensor for Minkowski space and of course, [math]\displaystyle{ \Lambda \in \operatorname{SO}(1, 3) }[/math] as before.
Covering groups
Since SL(2, C) is simply connected, it is the universal covering group of the restricted Lorentz group SO+(1, 3). By restriction, there is a homomorphism SU(2) → SO(3). Here, the special unitary group SU(2), which is isomorphic to the group of unit norm quaternions, is also simply connected, so it is the covering group of the rotation group SO(3). Each of these covering maps are twofold covers in the sense that precisely two elements of the covering group map to each element of the quotient. One often says that the restricted Lorentz group and the rotation group are doubly connected. This means that the fundamental group of the each group is isomorphic to the two-element cyclic group Z2.
Twofold coverings are characteristic of spin groups. Indeed, in addition to the double coverings
- Spin+(1, 3) = SL(2, C) → SO+(1, 3)
- Spin(3) = SU(2) → SO(3)
we have the double coverings
- Pin(1, 3) → O(1, 3)
- Spin(1, 3) → SO(1, 3)
- Spin+(1, 2) = SU(1, 1) → SO(1, 2)
These spinorial double coverings are constructed from Clifford algebras.
Topology
The left and right groups in the double covering
- SU(2) → SO(3)
are deformation retracts of the left and right groups, respectively, in the double covering
- SL(2, C) → SO+(1, 3).
But the homogeneous space SO+(1, 3) / SO(3) is homeomorphic to hyperbolic 3-space H3, so we have exhibited the restricted Lorentz group as a principal fiber bundle with fibers SO(3) and base H3. Since the latter is homeomorphic to R3, while SO(3) is homeomorphic to three-dimensional real projective space RP3, we see that the restricted Lorentz group is locally homeomorphic to the product of RP3 with R3. Since the base space is contractible, this can be extended to a global homeomorphism.[clarification needed]
Conjugacy classes
Because the restricted Lorentz group SO+(1, 3) is isomorphic to the Möbius group PSL(2, C), its conjugacy classes also fall into five classes:
- Elliptic transformations
- Hyperbolic transformations
- Loxodromic transformations
- Parabolic transformations
- The trivial identity transformation
In the article on Möbius transformations, it is explained how this classification arises by considering the fixed points of Möbius transformations in their action on the Riemann sphere, which corresponds here to null eigenspaces of restricted Lorentz transformations in their action on Minkowski spacetime.
An example of each type is given in the subsections below, along with the effect of the one-parameter subgroup it generates (e.g., on the appearance of the night sky).
The Möbius transformations are the conformal transformations of the Riemann sphere (or celestial sphere). Then conjugating with an arbitrary element of SL(2, C) obtains the following examples of arbitrary elliptic, hyperbolic, loxodromic, and parabolic (restricted) Lorentz transformations, respectively. The effect on the flow lines of the corresponding one-parameter subgroups is to transform the pattern seen in the examples by some conformal transformation. For example, an elliptic Lorentz transformation can have any two distinct fixed points on the celestial sphere, but points still flow along circular arcs from one fixed point toward the other. The other cases are similar.
Elliptic
An elliptic element of SL(2, C) is
- [math]\displaystyle{ P_1 = \begin{bmatrix} \exp\left(\frac{i}{2}\theta\right) & 0 \\ 0 & \exp\left(-\frac{i}{2}\theta\right) \end{bmatrix} }[/math]
and has fixed points ξ = 0, ∞. Writing the action as X ↦ P1 X P1† and collecting terms, the spinor map converts this to the (restricted) Lorentz transformation
- [math]\displaystyle{ Q_1 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\theta) & \sin(\theta) & 0 \\ 0 & -\sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \exp\left(\theta\begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}\right) ~. }[/math]
This transformation then represents a rotation about the z axis, exp(iθJz). The one-parameter subgroup it generates is obtained by taking θ to be a real variable, the rotation angle, instead of a constant.
The corresponding continuous transformations of the celestial sphere (except for the identity) all share the same two fixed points, the North and South poles. The transformations move all other points around latitude circles so that this group yields a continuous counter-clockwise rotation about the z axis as θ increases. The angle doubling evident in the spinor map is a characteristic feature of spinorial double coverings.
Hyperbolic
A hyperbolic element of SL(2, C) is
- [math]\displaystyle{ P_2 = \begin{bmatrix} \exp\left(\frac{\eta}{2}\right) & 0 \\ 0 & \exp\left(-\frac{\eta}{2}\right) \end{bmatrix} }[/math]
and has fixed points ξ = 0, ∞. Under stereographic projection from the Riemann sphere to the Euclidean plane, the effect of this Möbius transformation is a dilation from the origin.
The spinor map converts this to the Lorentz transformation
- [math]\displaystyle{ Q_2 = \begin{bmatrix} \cosh(\eta) & 0 & 0 & \sinh(\eta) \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \sinh(\eta) & 0 & 0 & \cosh(\eta) \end{bmatrix} = \exp \left( \eta \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix}\right)~. }[/math]
This transformation represents a boost along the z axis with rapidity η. The one-parameter subgroup it generates is obtained by taking η to be a real variable, instead of a constant. The corresponding continuous transformations of the celestial sphere (except for the identity) all share the same fixed points (the North and South poles), and they move all other points along longitudes away from the South pole and toward the North pole.
Loxodromic
A loxodromic element of SL(2, C) is
- [math]\displaystyle{ P_3 = P_2 P_1 = P_1 P_2 = \begin{bmatrix} \exp \left(\frac{1}{2}(\eta + i\theta)\right) & 0 \\ 0 & \exp \left(-\frac{1}{2}(\eta + i\theta)\right) \end{bmatrix} }[/math]
and has fixed points ξ = 0, ∞. The spinor map converts this to the Lorentz transformation
- [math]\displaystyle{ Q_3 = Q_2 Q_1 = Q_1 Q_2 = \begin{bmatrix} \cosh(\eta) & 0 & 0 & \sinh(\eta) \\ 0 & \cos(\theta) & \sin(\theta) & 0 \\ 0 & -\sin(\theta) & \cos(\theta) & 0 \\ \sinh(\eta) & 0 & 0 & \cosh(\eta) \end{bmatrix} = \exp\begin{bmatrix} 0 & 0 & 0 & \eta \\ 0 & 0 & \theta & 0 \\ 0 & -\theta & 0 & 0 \\ \eta & 0 & 0 & 0 \end{bmatrix} ~. }[/math]
The one-parameter subgroup this generates is obtained by replacing η + iθ with any real multiple of this complex constant. (If η, θ vary independently, then a two-dimensional abelian subgroup is obtained, consisting of simultaneous rotations about the z axis and boosts along the z-axis; in contrast, the one-dimensional subgroup discussed here consists of those elements of this two-dimensional subgroup such that the rapidity of the boost and angle of the rotation have a fixed ratio.)
The corresponding continuous transformations of the celestial sphere (excepting the identity) all share the same two fixed points (the North and South poles). They move all other points away from the South pole and toward the North pole (or vice versa), along a family of curves called loxodromes. Each loxodrome spirals infinitely often around each pole.
Parabolic
A parabolic element of SL(2, C) is
- [math]\displaystyle{ P_4 = \begin{bmatrix} 1 & \alpha \\ 0 & 1 \end{bmatrix} }[/math]
and has the single fixed point ξ = ∞ on the Riemann sphere. Under stereographic projection, it appears as an ordinary translation along the real axis.
The spinor map converts this to the matrix (representing a Lorentz transformation)
- [math]\displaystyle{ \begin{align} Q_4 &= \begin{bmatrix} 1 + \frac{1}{2}\vert\alpha\vert^2 & \operatorname{Re}(\alpha) & -\operatorname{Im}(\alpha) & -\frac{1}{2}\vert\alpha\vert^2 \\ \operatorname{Re}(\alpha) & 1 & 0 & -\operatorname{Re}(\alpha) \\ -\operatorname{Im}(\alpha) & 0 & 1 & \operatorname{Im}(\alpha) \\ \frac{1}{2}\vert\alpha\vert^2 & \operatorname{Re}(\alpha) & -\operatorname{Im}(\alpha) & 1 - \frac{1}{2}\vert\alpha\vert^2 \end{bmatrix} \\[6pt] &= \exp \begin{bmatrix} 0 & \operatorname{Re}(\alpha) & -\operatorname{Im}(\alpha) & 0 \\ \operatorname{Re}(\alpha) & 0 & 0 & -\operatorname{Re}(\alpha) \\ -\operatorname{Im}(\alpha) & 0 & 0 & \operatorname{Im}(\alpha) \\ 0 & \operatorname{Re}(\alpha) & -\operatorname{Im}(\alpha) & 0 \end{bmatrix} ~. \end{align} }[/math]
This generates a two-parameter abelian subgroup, which is obtained by considering α a complex variable rather than a constant. The corresponding continuous transformations of the celestial sphere (except for the identity transformation) move points along a family of circles that are all tangent at the North pole to a certain great circle. All points other than the North pole itself move along these circles.
Parabolic Lorentz transformations are often called null rotations. Since these are likely to be the least familiar of the four types of nonidentity Lorentz transformations (elliptic, hyperbolic, loxodromic, parabolic), it is illustrated here how to determine the effect of an example of a parabolic Lorentz transformation on Minkowski spacetime.
The matrix given above yields the transformation
- [math]\displaystyle{ \begin{bmatrix} t \\ x \\ y \\ z \end{bmatrix} \rightarrow \begin{bmatrix} t \\ x \\ y \\ z \end{bmatrix} + \operatorname{Re}(\alpha) \; \begin{bmatrix} x \\ t - z \\ 0 \\ x \end{bmatrix} - \operatorname{Im}(\alpha) \; \begin{bmatrix} y \\ 0 \\ z - t \\ y \end{bmatrix} + \frac{\vert\alpha\vert^2}{2} \; \begin{bmatrix} t - z \\ 0 \\ 0 \\ t - z \end{bmatrix}. }[/math]
Now, without loss of generality, pick Im(α) = 0. Differentiating this transformation with respect to the now real group parameter α and evaluating at α = 0 produces the corresponding vector field (first order linear partial differential operator),
- [math]\displaystyle{ x\, \left( \partial_t + \partial_z \right) + (t - z)\, \partial_x. }[/math]
Apply this to a function f(t, x, y, z), and demand that it stays invariant; i.e., it is annihilated by this transformation. The solution of the resulting first order linear partial differential equation can be expressed in the form
- [math]\displaystyle{ f(t, x, y, z) = F\left(y,\, t - z,\, t^2 - x^2 - z^2\right), }[/math]
where F is an arbitrary smooth function. The arguments of F give three rational invariants describing how points (events) move under this parabolic transformation, as they themselves do not move,
- [math]\displaystyle{ y = c_1, ~~~~ t-z = c_2, ~~~~ t^2 - x^2 - z^2 = c_3. }[/math]
Choosing real values for the constants on the right hand sides yields three conditions, and thus specifies a curve in Minkowski spacetime. This curve is an orbit of the transformation.
The form of the rational invariants shows that these flowlines (orbits) have a simple description: suppressing the inessential coordinate y, each orbit is the intersection of a null plane, t = z + c2, with a hyperboloid, t2 − x2 − z2 = c3. The case c3 = 0 has the hyperboloid degenerate to a light cone with the orbits becoming parabolas lying in corresponding null planes.
A particular null line lying on the light cone is left invariant; this corresponds to the unique (double) fixed point on the Riemann sphere mentioned above. The other null lines through the origin are "swung around the cone" by the transformation. Following the motion of one such null line as α increases corresponds to following the motion of a point along one of the circular flow lines on the celestial sphere, as described above.
A choice Re(α) = 0 instead, produces similar orbits, now with the roles of x and y interchanged.
Parabolic transformations lead to the gauge symmetry of massless particles (such as photons) with helicity |h| ≥ 1. In the above explicit example, a massless particle moving in the z direction, so with 4-momentum P = (p, 0, 0, p), is not affected at all by the x-boost and y-rotation combination Kx − Jy defined below, in the "little group" of its motion. This is evident from the explicit transformation law discussed: like any light-like vector, P itself is now invariant; i.e., all traces or effects of α have disappeared. c1 = c2 = c3 = 0, in the special case discussed. (The other similar generator, Ky + Jx as well as it and Jz comprise altogether the little group of the light-like vector, isomorphic to E(2).)
Appearance of the night sky
This isomorphism has the consequence that Möbius transformations of the Riemann sphere represent the way that Lorentz transformations change the appearance of the night sky, as seen by an observer who is maneuvering at relativistic velocities relative to the "fixed stars".
Suppose the "fixed stars" live in Minkowski spacetime and are modeled by points on the celestial sphere. Then a given point on the celestial sphere can be associated with ξ = u + iv, a complex number that corresponds to the point on the Riemann sphere, and can be identified with a null vector (a light-like vector) in Minkowski space
- [math]\displaystyle{ \begin{bmatrix} u^2 + v^2 + 1 \\ 2u \\ -2v \\ u^2 + v^2 - 1 \end{bmatrix} }[/math]
or, in the Weyl representation (the spinor map), the Hermitian matrix
- [math]\displaystyle{ N = 2\begin{bmatrix} u^2 + v^2 & u + iv \\ u - iv & 1 \end{bmatrix}. }[/math]

The set of real scalar multiples of this null vector, called a null line through the origin, represents a line of sight from an observer at a particular place and time (an arbitrary event we can identify with the origin of Minkowski spacetime) to various distant objects, such as stars. Then the points of the celestial sphere (equivalently, lines of sight) are identified with certain Hermitian matrices.
Projective geometry and different views of the 2-sphere
This picture emerges cleanly in the language of projective geometry. The (restricted) Lorentz group acts on the projective celestial sphere. This is the space of non-zero null vectors with [math]\displaystyle{ t\gt 0 }[/math] under the given quotient for projective spaces: [math]\displaystyle{ (t,x,y,z)\sim (t',x',y',z') }[/math] if [math]\displaystyle{ (t',x',y',z') = (\lambda t, \lambda x, \lambda y, \lambda z) }[/math] for [math]\displaystyle{ \lambda \gt 0 }[/math]. This is referred to as the celestial sphere as this allows us to rescale the time coordinate [math]\displaystyle{ t }[/math] to 1 after acting using a Lorentz transformation, ensuring the space-like part sits on the unit sphere.
From the Möbius side, SL(2, C) acts on complex projective space CP1, which can be shown to be diffeomorphic to the 2-sphere – this is sometimes referred to as the Riemann sphere. The quotient on projective space leads to a quotient on the group SL(2, C).
Finally, these two can be linked together by using the complex projective vector to construct a null-vector. If [math]\displaystyle{ \xi }[/math] is a CP1 projective vector, it can be tensored with its Hermitian conjugate to produce a [math]\displaystyle{ 2\times 2 }[/math] Hermitian matrix. From elsewhere in this article we know this space of matrices can be viewed as 4-vectors. The space of matrices coming from turning each projective vector in the Riemann sphere into a matrix is known as the Bloch sphere.
Lie algebra
| Group theory → Lie groups Lie groups |
|---|
 |
As with any Lie group, a useful way to study many aspects of the Lorentz group is via its Lie algebra. Since the Lorentz group SO(1, 3) is a matrix Lie group, its corresponding Lie algebra [math]\displaystyle{ \mathfrak{so}(1,3) }[/math] is a matrix Lie algebra, which may be computed as[5]
- [math]\displaystyle{ \mathfrak{so}(1,3) = \left\{4\times 4\,\,\, \mathbf{R}\text{-valued matrices}\, X \mid e^{tX} \in \mathrm{SO}(1,3)\,\mathrm{for}\,\mathrm{all}\, t\right\} }[/math].
If [math]\displaystyle{ \eta }[/math] is the diagonal matrix with diagonal entries (1, −1, −1, −1), then the Lie algebra [math]\displaystyle{ \mathfrak{o}(1,3) }[/math] consists of [math]\displaystyle{ 4\times 4 }[/math] matrices [math]\displaystyle{ X }[/math] such that[6]
- [math]\displaystyle{ \eta X \eta = -X^\textsf{T} }[/math].
Explicitly, [math]\displaystyle{ \mathfrak{so}(1, 3) }[/math] consists of [math]\displaystyle{ 4\times 4 }[/math] matrices of the form
- [math]\displaystyle{ \begin{pmatrix} 0 & a & b & c \\ a & 0 & d & e \\ b & -d & 0 & f \\ c & -e & -f & 0 \end{pmatrix} }[/math],
where [math]\displaystyle{ a, b, c, d, e, f }[/math] are arbitrary real numbers. This Lie algebra is six dimensional. The subalgebra of [math]\displaystyle{ \mathfrak{so}(1, 3) }[/math] consisting of elements in which [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math], and [math]\displaystyle{ c }[/math] equal to zero is isomorphic to [math]\displaystyle{ \mathfrak{so}(3) }[/math].
The full Lorentz group O(1, 3), the proper Lorentz group SO(1, 3) and the proper orthochronous Lorentz group SO+(1, 3) (the component connected to the identity) all have the same Lie algebra, which is typically denoted [math]\displaystyle{ \mathfrak{so}(1,3) }[/math].
Since the identity component of the Lorentz group is isomorphic to a finite quotient of SL(2, C) (see the section above on the connection of the Lorentz group to the Möbius group), the Lie algebra of the Lorentz group is isomorphic to the Lie algebra [math]\displaystyle{ \mathfrak{sl}(2, \mathbf{C}) }[/math]. As a complex Lie algebra [math]\displaystyle{ \mathfrak{sl}(2, \mathbf{C}) }[/math] is three dimensional, but is six dimensional when viewed as a real Lie algebra.
Commutation relations of the Lorentz algebra
The standard basis matrices can be indexed as [math]\displaystyle{ M^{\mu\nu} }[/math] where [math]\displaystyle{ \mu,\nu }[/math] take values in {0, 1, 2, 3}. These arise from taking only one of [math]\displaystyle{ a,b,\cdots, f }[/math] to be one, and others zero, in turn. The components can be written as
- [math]\displaystyle{ (M^{\mu\nu})_{\rho\sigma} = \delta^\mu{}_\rho\delta^\nu{}_\sigma - \delta^\nu{}_\rho\delta^\mu{}_\sigma }[/math].
The commutation relations are
- [math]\displaystyle{ [M^{\mu\nu},M^{\rho\sigma}] = M^{\mu\sigma}\eta^{\nu\rho} - M^{\nu\sigma}\eta^{\mu\rho} + M^{\nu\rho}\eta^{\mu\sigma} - M^{\mu\rho}\eta^{\nu\sigma}. }[/math]
There are different possible choices of convention in use. In physics, it is common to include a factor of [math]\displaystyle{ i }[/math] with the basis elements, which gives a factor of [math]\displaystyle{ i }[/math] in the commutation relations.
Then [math]\displaystyle{ M^{0i} }[/math] generate boosts and [math]\displaystyle{ M^{ij} }[/math] generate rotations.
The structure constants for the Lorentz algebra can be read off from the commutation relations. Any set of basis elements which satisfy these relations form a representation of the Lorentz algebra.
Generators of boosts and rotations
The Lorentz group can be thought of as a subgroup of the diffeomorphism group of R4 and therefore its Lie algebra can be identified with vector fields on R4. In particular, the vectors that generate isometries on a space are its Killing vectors, which provides a convenient alternative to the left-invariant vector field for calculating the Lie algebra. We can write down a set of six generators:
- Vector fields on R4 generating three rotations iJ,
- [math]\displaystyle{ -y \partial_x + x \partial_y \equiv i J_z ~, \qquad -z \partial_y + y \partial_z \equiv iJ_x~, \qquad -x \partial_z + z \partial_x \equiv iJ_y ~; }[/math]
- Vector fields on R4 generating three boosts iK,
- [math]\displaystyle{ x \partial_t + t \partial_x\equiv iK_x ~, \qquad y \partial_t + t \partial_y \equiv iK_y ~, \qquad z \partial_t + t \partial_z\equiv iK_z. }[/math]
The factor of i appears to ensure that the generators of rotations are Hermitian.
It may be helpful to briefly recall here how to obtain a one-parameter group from a vector field, written in the form of a first order linear partial differential operator such as
- [math]\displaystyle{ \mathcal{L} = -y \partial_x + x \partial_y. }[/math]
The corresponding initial value problem (consider [math]\displaystyle{ r = (x, y) }[/math] a function of a scalar [math]\displaystyle{ \lambda }[/math] and solve [math]\displaystyle{ \partial_{\lambda} r = \mathcal{L} r }[/math] with some initial conditions) is
- [math]\displaystyle{ \frac{\partial x}{\partial \lambda} = -y, \; \frac{\partial y}{\partial \lambda} = x, \; x(0) = x_0, \; y(0) = y_0. }[/math]
The solution can be written
- [math]\displaystyle{ x(\lambda) = x_0 \cos(\lambda) - y_0 \sin(\lambda), \; y(\lambda) = x_0 \sin(\lambda) + y_0 \cos(\lambda) }[/math]
or
- [math]\displaystyle{ \begin{bmatrix} t \\ x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\lambda) & -\sin(\lambda) & 0 \\ 0 & \sin(\lambda) & \cos(\lambda) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} t_0 \\ x_0 \\ y_0 \\ z_0 \end{bmatrix} }[/math]
where we easily recognize the one-parameter matrix group of rotations exp(iλJz) about the z-axis.
Differentiating with respect to the group parameter λ and setting it λ = 0 in that result, we recover the standard matrix,
- [math]\displaystyle{ iJ_z = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} ~, }[/math]
which corresponds to the vector field we started with. This illustrates how to pass between matrix and vector field representations of elements of the Lie algebra. The exponential map plays this special role not only for the Lorentz group but for Lie groups in general.
Reversing the procedure in the previous section, we see that the Möbius transformations that correspond to our six generators arise from exponentiating respectively η/2 (for the three boosts) or iθ/2 (for the three rotations) times the three Pauli matrices
- [math]\displaystyle{ \sigma_1 = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}, \;\; \sigma_2 = \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}, \;\; \sigma_3 = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}. }[/math]
Generators of the Möbius group
Another generating set arises via the isomorphism to the Möbius group. The following table lists the six generators, in which
- The first column gives a generator of the flow under the Möbius action (after stereographic projection from the Riemann sphere) as a real vector field on the Euclidean plane.
- The second column gives the corresponding one-parameter subgroup of Möbius transformations.
- The third column gives the corresponding one-parameter subgroup of Lorentz transformations (the image under our homomorphism of preceding one-parameter subgroup).
- The fourth column gives the corresponding generator of the flow under the Lorentz action as a real vector field on Minkowski spacetime.
Notice that the generators consist of
- Two parabolics (null rotations)
- One hyperbolic (boost in the [math]\displaystyle{ \partial_z }[/math] direction)
- Three elliptics (rotations about the x, y, z axes, respectively)
| Vector field on R2 | One-parameter subgroup of SL(2, C), representing Möbius transformations |
One-parameter subgroup of SO+(1, 3), representing Lorentz transformations |
Vector field on R1,3 |
|---|---|---|---|
| Parabolic | |||
| [math]\displaystyle{ \partial_u\,\! }[/math] | [math]\displaystyle{ \begin{bmatrix} 1 & \alpha \\ 0 & 1 \end{bmatrix} }[/math] | [math]\displaystyle{ \begin{bmatrix} 1 + \frac{1}{2}\alpha^2 & \alpha & 0 & -\frac{1}{2}\alpha^2 \\ \alpha & 1 & 0 & -\alpha \\ 0 & 0 & 1 & 0 \\ \frac{1}{2}\alpha^2 & \alpha & 0 & 1 - \frac{1}{2}\alpha^2 \end{bmatrix} }[/math] | [math]\displaystyle{ \begin{align} X_1 = x&(\partial_t + \partial_z) +{}\\ &(t - z)\partial_x \end{align} }[/math] |
| [math]\displaystyle{ \partial_v\,\! }[/math] | [math]\displaystyle{ \begin{bmatrix} 1 & i \alpha \\ 0 & 1 \end{bmatrix} }[/math] | [math]\displaystyle{ \begin{bmatrix} 1 + \frac{1}{2}\alpha^2 & 0 & \alpha & -\frac{1}{2}\alpha^2 \\ 0 & 1 & 0 & 0 \\ \alpha & 0 & 1 & -\alpha \\ \frac{1}{2}\alpha^2 & 0 & \alpha & 1 - \frac{1}{2}\alpha^2 \end{bmatrix} }[/math] | [math]\displaystyle{ \begin{align} X_2 = y&(\partial_t + \partial_z) +{}\\ &(t - z)\partial_y \end{align} }[/math] |
| Hyperbolic | |||
| [math]\displaystyle{ \frac{1}{2} \left( u \partial_u + v \partial_v \right) }[/math] | [math]\displaystyle{ \begin{bmatrix} \exp \left(\frac{\eta}{2}\right) & 0 \\ 0 & \exp \left(-\frac{\eta}{2}\right) \end{bmatrix} }[/math] | [math]\displaystyle{ \begin{bmatrix} \cosh(\eta) & 0 & 0 & \sinh(\eta) \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \sinh(\eta) & 0 & 0 & \cosh(\eta) \end{bmatrix} }[/math] | [math]\displaystyle{ X_3 = z \partial_t + t \partial_z \,\! }[/math] |
| Elliptic | |||
| [math]\displaystyle{ \frac{1}{2} \left( -v \partial_u + u \partial_v \right) }[/math] | [math]\displaystyle{ \begin{bmatrix} \exp \left( \frac{i \theta}{2} \right) & 0 \\ 0 & \exp \left( \frac{-i \theta}{2} \right) \end{bmatrix} }[/math] | [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) & 0 \\ 0 & \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} }[/math] | [math]\displaystyle{ X_4 = -y\partial_x + x\partial_y }[/math] |
| [math]\displaystyle{ \frac{v^2 - u^2 - 1}{2} \partial_u - u v \, \partial_v }[/math] | [math]\displaystyle{ \begin{bmatrix} \cos \left( \frac{\theta}{2} \right) & -\sin \left( \frac{\theta}{2} \right) \\ \sin \left( \frac{\theta}{2} \right) & \cos \left( \frac{\theta}{2} \right) \end{bmatrix} }[/math] | [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\theta) & 0 & \sin(\theta) \\ 0 & 0 & 1 & 0 \\ 0 & -\sin(\theta) & 0 & \cos(\theta) \end{bmatrix} }[/math] | [math]\displaystyle{ X_5 = -x\partial_z + z\partial_x }[/math] |
| [math]\displaystyle{ u v \, \partial_u + \frac{1 - u^2 + v^2}{2} \partial_v }[/math] | [math]\displaystyle{ \begin{bmatrix} \cos \left( \frac{\theta}{2} \right) & i \sin \left( \frac{\theta}{2} \right) \\ i \sin \left( \frac{\theta}{2} \right) & \cos \left( \frac{\theta}{2} \right) \end{bmatrix} }[/math] | [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \cos(\theta) & -\sin(\theta) \\ 0 & 0 & \sin(\theta) & \cos(\theta) \end{bmatrix} }[/math] | [math]\displaystyle{ X_6 = -z\partial_y + y\partial_z }[/math] |
Worked example: rotation about the y-axis
Start with
- [math]\displaystyle{ \sigma_2 = \begin{bmatrix} 0 & i \\ -i & 0 \end{bmatrix}. }[/math]
Exponentiate:
- [math]\displaystyle{ \exp \left( \frac{ i \theta}{2} \, \sigma_2 \right) = \begin{bmatrix} \cos\left(\frac{\theta}{2}\right) & -\sin\left(\frac{\theta}{2}\right) \\ \sin\left(\frac{\theta}{2}\right) & \cos\left(\frac{\theta}{2}\right) \end{bmatrix}. }[/math]
This element of SL(2, C) represents the one-parameter subgroup of (elliptic) Möbius transformations:
- [math]\displaystyle{ \xi \mapsto \xi' = \frac{ \cos\left(\frac{\theta}{2}\right) \, \xi - \sin\left(\frac{\theta}{2}\right) }{ \sin\left(\frac{\theta}{2}\right) \, \xi + \cos\left(\frac{\theta}{2}\right) }. }[/math]
Next,
- [math]\displaystyle{ \left.\frac{d\xi'}{d\theta}\right|_{\theta=0} = -\frac{1 + \xi^2}{2}. }[/math]
The corresponding vector field on C (thought of as the image of S2 under stereographic projection) is
- [math]\displaystyle{ -\frac{1 + \xi^2}{2} \, \partial_\xi. }[/math]
Writing [math]\displaystyle{ \xi = u + i v }[/math], this becomes the vector field on R2
- [math]\displaystyle{ -\frac{1 + u^2 - v^2}{2} \, \partial_u - u v \, \partial_v. }[/math]
Returning to our element of SL(2, C), writing out the action [math]\displaystyle{ X \mapsto P X P^\dagger }[/math] and collecting terms, we find that the image under the spinor map is the element of SO+(1, 3)
- [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\theta) & 0 & \sin(\theta) \\ 0 & 0 & 1 & 0 \\ 0 & -\sin(\theta) & 0 & \cos(\theta) \end{bmatrix}. }[/math]
Differentiating with respect to θ at θ = 0, yields the corresponding vector field on R1,3,
- [math]\displaystyle{ z \partial_x - x \partial_z. \,\! }[/math]
This is evidently the generator of counterclockwise rotation about the y-axis.
Subgroups of the Lorentz group
The subalgebras of the Lie algebra of the Lorentz group can be enumerated, up to conjugacy, from which the closed subgroups of the restricted Lorentz group can be listed, up to conjugacy. (See the book by Hall cited below for the details.) These can be readily expressed in terms of the generators [math]\displaystyle{ X_n }[/math] given in the table above.
The one-dimensional subalgebras of course correspond to the four conjugacy classes of elements of the Lorentz group:
- [math]\displaystyle{ X_1 }[/math] generates a one-parameter subalgebra of parabolics SO(0, 1),
- [math]\displaystyle{ X_3 }[/math] generates a one-parameter subalgebra of boosts SO(1, 1),
- [math]\displaystyle{ X_4 }[/math] generates a one-parameter of rotations SO(2),
- [math]\displaystyle{ X_3 + a X_4 }[/math] (for any [math]\displaystyle{ a \neq 0 }[/math]) generates a one-parameter subalgebra of loxodromic transformations.
(Strictly speaking the last corresponds to infinitely many classes, since distinct [math]\displaystyle{ a }[/math] give different classes.) The two-dimensional subalgebras are:
- [math]\displaystyle{ X_1, X_2 }[/math] generate an abelian subalgebra consisting entirely of parabolics,
- [math]\displaystyle{ X_1, X_3 }[/math] generate a nonabelian subalgebra isomorphic to the Lie algebra of the affine group Aff(1),
- [math]\displaystyle{ X_3, X_4 }[/math] generate an abelian subalgebra consisting of boosts, rotations, and loxodromics all sharing the same pair of fixed points.
The three-dimensional subalgebras use the Bianchi classification scheme:
- [math]\displaystyle{ X_1, X_2, X_3 }[/math] generate a Bianchi V subalgebra, isomorphic to the Lie algebra of Hom(2), the group of euclidean homotheties,
- [math]\displaystyle{ X_1, X_2, X_4 }[/math] generate a Bianchi VII0 subalgebra, isomorphic to the Lie algebra of E(2), the euclidean group,
- [math]\displaystyle{ X_1, X_2, X_3 + a X_4 }[/math], where [math]\displaystyle{ a \neq 0 }[/math], generate a Bianchi VIIa subalgebra,
- [math]\displaystyle{ X_1, X_3, X_5 }[/math] generate a Bianchi VIII subalgebra, isomorphic to the Lie algebra of SL(2, R), the group of isometries of the hyperbolic plane,
- [math]\displaystyle{ X_4, X_5, X_6 }[/math] generate a Bianchi IX subalgebra, isomorphic to the Lie algebra of SO(3), the rotation group.
The Bianchi types refer to the classification of three-dimensional Lie algebras by the Italian mathematician Luigi Bianchi.
The four-dimensional subalgebras are all conjugate to
- [math]\displaystyle{ X_1, X_2, X_3, X_4 }[/math] generate a subalgebra isomorphic to the Lie algebra of Sim(2), the group of Euclidean similitudes.
The subalgebras form a lattice (see the figure), and each subalgebra generates by exponentiation a closed subgroup of the restricted Lie group. From these, all subgroups of the Lorentz group can be constructed, up to conjugation, by multiplying by one of the elements of the Klein four-group.
As with any connected Lie group, the coset spaces of the closed subgroups of the restricted Lorentz group, or homogeneous spaces, have considerable mathematical interest. A few, brief descriptions:
- The group Sim(2) is the stabilizer of a null line; i.e., of a point on the Riemann sphere—so the homogeneous space SO+(1, 3) / Sim(2) is the Kleinian geometry that represents conformal geometry on the sphere S2.
- The (identity component of the) Euclidean group SE(2) is the stabilizer of a null vector, so the homogeneous space SO+(1, 3) / SE(2) is the momentum space of a massless particle; geometrically, this Kleinian geometry represents the degenerate geometry of the light cone in Minkowski spacetime.
- The rotation group SO(3) is the stabilizer of a timelike vector, so the homogeneous space SO+(1, 3) / SO(3) is the momentum space of a massive particle; geometrically, this space is none other than three-dimensional hyperbolic space H3.
Generalization to higher dimensions
The concept of the Lorentz group has a natural generalization to spacetime of any number of dimensions. Mathematically, the Lorentz group of (n + 1)-dimensional Minkowski space is the indefinite orthogonal group O(n, 1) of linear transformations of Rn+1 that preserves the quadratic form
- [math]\displaystyle{ (x_1, x_2, \ldots, x_n, x_{n+1}) \mapsto x_1^2 + x_2^2 + \cdots + x_n^2 - x_{n+1}^2. }[/math]
The group O(1, n) preserves the quadratic form
- [math]\displaystyle{ (x_1, x_2, \ldots, x_n, x_{n+1}) \mapsto x_1^2 - x_2^2 - \cdots - x_{n+1}^2 }[/math]
O(1, n) is isomorphic to O(n, 1), and both presentations of the Lorentz group are in use in the theoretical physics community. The former is more common in literature related to gravity, while the latter is more common in particle physics literature.
A common notation for the vector space Rn+1, equipped with this choice of quadratic form, is R1,n.
Many of the properties of the Lorentz group in four dimensions (where n = 3) generalize straightforwardly to arbitrary n. For instance, the Lorentz group O(n, 1) has four connected components, and it acts by conformal transformations on the celestial (n − 1)-sphere in (n + 1)-dimensional Minkowski space. The identity component SO+(n, 1) is an SO(n)-bundle over hyperbolic n-space Hn.
The low-dimensional cases n = 1 and n = 2 are often useful as "toy models" for the physical case n = 3, while higher-dimensional Lorentz groups are used in physical theories such as string theory that posit the existence of hidden dimensions. The Lorentz group O(n, 1) is also the isometry group of n-dimensional de Sitter space dSn, which may be realized as the homogeneous space O(n, 1) / O(n − 1, 1). In particular O(4, 1) is the isometry group of the de Sitter universe dS4, a cosmological model.
See also
- Lorentz transformation
- Lorentz group representation theory
- Poincaré group
- Möbius group
- Minkowski space
- Biquaternions
- Indefinite orthogonal group
- Quaternions and spatial rotation
- Special relativity
- Symmetry in quantum mechanics
Notes
- ↑ Note that some authors refer to SO(1, 3) or even O(1, 3) when they mean SO+(1, 3).
- ↑ See the article Weyl equation for explicit derivations.
References
- ↑ Weinberg 2002
- ↑ Varićak V 1910 "Theory of Relativity and Lobachevskian geometry", Phys Z 1910 §3 'Lorentz-Einstein transformation as translation'. Engl.tr in Wikipedia
- ↑ Gelfand, Minlos & Shapiro 1963
- ↑ Wigner 1939
- ↑ Hall 2015 Definition 3.18
- ↑ Hall 2015 Proposition 3.25
Reading List
- Emil Artin (1957) Geometric Algebra, chapter III: Symplectic and Orthogonal Geometry via Internet Archive, covers orthogonal groups O(p, q)
- Carmeli, Moshe (1977). Group Theory and General Relativity, Representations of the Lorentz Group and Their Applications to the Gravitational Field. McGraw-Hill, New York. ISBN 978-0-07-009986-9. A canonical reference; see chapters 1–6 for representations of the Lorentz group.
- Frankel, Theodore (2004). The Geometry of Physics (2nd Ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-53927-2. An excellent resource for Lie theory, fiber bundles, spinorial coverings, and many other topics.
- Fulton, William; Harris, Joe (1991) (in en-gb). Representation theory. A first course. Graduate Texts in Mathematics, Readings in Mathematics. 129. New York: Springer-Verlag. doi:10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. OCLC 246650103. https://link.springer.com/10.1007/978-1-4612-0979-9. See Lecture 11 for the irreducible representations of SL(2, C).
- Gelfand, I.M.; Minlos, R.A.; Shapiro, Z.Ya. (1963), Representations of the Rotation and Lorentz Groups and their Applications, New York: Pergamon Press
- Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, 222 (2nd ed.), Springer, ISBN 978-3319134666
- Hall, G. S. (2004). Symmetries and Curvature Structure in General Relativity. Singapore: World Scientific. ISBN 978-981-02-1051-9. See Chapter 6 for the subalgebras of the Lie algebra of the Lorentz group.
- Hatcher, Allen (2002). Algebraic topology. Cambridge: Cambridge University Press. ISBN 978-0-521-79540-1. See also the "online version". http://www.math.cornell.edu/~hatcher/AT/ATpage.html. See Section 1.3 for a beautifully illustrated discussion of covering spaces. See Section 3D for the topology of rotation groups.
- Misner, Charles; Thorne, Kip S.; Wheeler, John (1973). Gravitation. W. H. Freeman and Company. ISBN 978-0-7167-0344-0. §41.3
- Naber, Gregory (1992). The Geometry of Minkowski Spacetime. New York: Springer-Verlag. ISBN 978-0486432359. (Dover reprint edition.) An excellent reference on Minkowski spacetime and the Lorentz group.
- Needham, Tristan (1997). Visual Complex Analysis. Oxford: Oxford University Press. ISBN 978-0-19-853446-4. See Chapter 3 for a superbly illustrated discussion of Möbius transformations.
- Weinberg, S. (2002), The Quantum Theory of Fields, 1, Cambridge University Press, ISBN 978-0-521-55001-7, https://archive.org/details/quantumtheoryoff00stev
- Wigner, E. P. (1939), "On unitary representations of the inhomogeneous Lorentz group", Annals of Mathematics 40 (1): 149–204, doi:10.2307/1968551, Bibcode: 1939AnMat..40..149W
 |