Physics:Electroweak interaction

Short description: Unified description of electromagnetism and the weak interaction

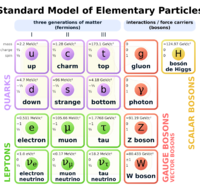In particle physics, the electroweak interaction or electroweak force is the unified description of two of the four known fundamental interactions of nature: electromagnetism (electromagnetic interaction) and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different aspects of the same force. Above the unification energy, on the order of 246 GeV, they would merge into a single force. Thus, if the temperature is high enough – approximately 10¹⁵ K – then the electromagnetic force and weak force merge into a combined electroweak force. During the quark epoch (shortly after the Big Bang), the electroweak force split into the electromagnetic and weak force. It is thought that the required temperature of 10¹⁵ K has not been seen widely throughout the universe since before the quark epoch, and currently the highest human-made temperature in thermal equilibrium is around 5.5x10¹² K (from the Large Hadron Collider).

Sheldon Glashow, Abdus Salam, and Steven Weinberg were awarded the 1979 Nobel Prize in Physics for their contributions to the unification of the weak and electromagnetic interaction between elementary particles, known as the Weinberg–Salam theory. The existence of the electroweak interactions was experimentally established in two stages, the first being the discovery of neutral currents in neutrino scattering by the Gargamelle collaboration in 1973, and the second in 1983 by the UA1 and the UA2 collaborations that involved the discovery of the W and Z gauge bosons in proton–antiproton collisions at the converted Super Proton Synchrotron. In 1999, Gerardus 't Hooft and Martinus Veltman were awarded the Nobel prize for showing that the electroweak theory is renormalizable.

History

After the Wu experiment in 1956 discovered parity violation in the weak interaction, a search began for a way to relate the weak and electromagnetic interactions. Extending his doctoral advisor Julian Schwinger's work, Sheldon Glashow first experimented with introducing two different symmetries, one chiral and one achiral, and combined them such that their overall symmetry was unbroken. This did not yield a renormalizable theory, and its gauge symmetry had to be broken by hand as no spontaneous mechanism was known, but it predicted a new particle, the Z boson. This received little notice, as it matched no experimental finding.

In 1964, Salam and John Clive Ward had the same idea, but predicted a massless photon and three massive gauge bosons with a manually broken symmetry. Later around 1967, while investigating spontaneous symmetry breaking, Weinberg found a set of symmetries predicting a massless, neutral gauge boson. Initially rejecting such a particle as useless, he later realized his symmetries produced the electroweak force, and he proceeded to predict rough masses for the W and Z bosons. Significantly, he suggested this new theory was renormalizable. In 1971, Gerard 't Hooft proved that spontaneously broken gauge symmetries are renormalizable even with massive gauge bosons.

Formulation

Weinberg's weak mixing angle θ_W, and relation between coupling constants g, g′, and e. Adapted from Lee (1981).

The pattern of weak isospin, T₃, and weak hypercharge, Y_W, of the known elementary particles, showing the electric charge, Q, along the weak mixing angle. The neutral Higgs field (circled) breaks the electroweak symmetry and interacts with other particles to give them mass. Three components of the Higgs field become part of the massive W and Z bosons.

Mathematically, electromagnetism is unified with the weak interactions as a Yang–Mills field with an SU(2) × U(1) gauge group, which describes the formal operations that can be applied to the electroweak gauge fields without changing the dynamics of the system. These fields are the weak isospin fields W₁, W₂, and W₃, and the weak hypercharge field B. This invariance is known as electroweak symmetry.

The generators of SU(2) and U(1) are given the name weak isospin (labeled T ) and weak hypercharge (labeled Y ) respectively. These then give rise to the gauge bosons which mediate the electroweak interactions – the three W bosons of weak isospin (W₁, W₂, and W₃), and the B boson of weak hypercharge, respectively, all of which are "initially" massless. These are not physical fields yet, before spontaneous symmetry breaking and the associated Higgs mechanism.

In the Standard Model, the observed physical particles, the W^± and Z⁰ bosons, and the photon, are produced through the spontaneous symmetry breaking of the electroweak symmetry SU(2) × U(1)_Y to U(1)_em, effected by the Higgs mechanism (see also Higgs boson), an elaborate quantum-field-theoretic phenomenon that "spontaneously" alters the realization of the symmetry and rearranges degrees of freedom.

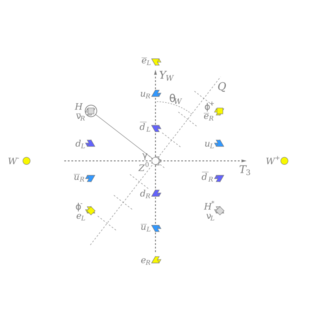
The electric charge arises as the particular linear combination (nontrivial) of Y_W (weak hypercharge) and the T₃ component of weak isospin [math]\displaystyle{ ~ \left(\, Q = T_3 + \tfrac{1}{2}\,Y_\mathrm{W}\,\right) ~ }[/math] that does not couple to the Higgs boson. That is to say: The Higgs and the electromagnetic field have no effect on each other, at the level of the fundamental forces ("tree level"), while any other combination of the hypercharge and the weak isospin must interact with the Higgs. This causes an apparent separation between the weak force, which interacts with the Higgs, and electromagnetism, which does not. Mathematically, the electric charge is a specific combination of the hypercharge and T₃ outlined in the figure.

U(1)_em (the symmetry group of electromagnetism only) is defined to be the group generated by this special linear combination, and the symmetry described by the U(1)_em group is unbroken, since it does not directly interact with the Higgs.

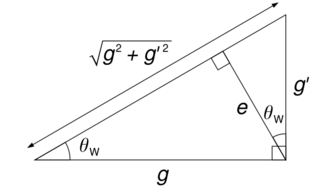
The above spontaneous symmetry breaking makes the W₃ and B bosons coalesce into two different physical bosons with different masses – the Z⁰ boson, and the photon (γ),

[math]\displaystyle{ \begin{pmatrix} \gamma \\ Z^0 \end{pmatrix} = \begin{pmatrix} \cos \theta_\text{W} & \sin \theta_\text{W} \\ -\sin \theta_\text{W} & \cos \theta_\text{W} \end{pmatrix} \begin{pmatrix} B \\ W_3 \end{pmatrix} , }[/math]

where θ_W is the weak mixing angle. The axes representing the particles have essentially just been rotated, in the (W₃, B) plane, by the angle θ_W. This also introduces a mismatch between the mass of the Z⁰ and the mass of the W^± particles (denoted as m_Z and m_W, respectively),

[math]\displaystyle{ m_\text{Z} = \frac{m_\text{W}}{\,\cos\theta_\text{W}\,} ~. }[/math]

The W₁ and W₂ bosons, in turn, combine to produce the charged massive bosons W^±:

[math]\displaystyle{ W^{\pm} = \frac{1}{\sqrt{2\,}}\,\bigl(\,W_1 \mp i W_2\,\bigr) ~. }[/math]

Lagrangian

Before electroweak symmetry breaking

The Lagrangian for the electroweak interactions is divided into four parts before electroweak symmetry breaking becomes manifest,

[math]\displaystyle{ \mathcal{L}_{\mathrm{EW}} = \mathcal{L}_g + \mathcal{L}_f + \mathcal{L}_h + \mathcal{L}_y~. }[/math]

The [math]\displaystyle{ \mathcal{L}_g }[/math] term describes the interaction between the three W vector bosons and the B vector boson,

[math]\displaystyle{ \mathcal{L}_g = -\tfrac{1}{4} W_{a}^{\mu\nu}W_{\mu\nu}^a - \tfrac{1}{4} B^{\mu\nu}B_{\mu\nu} }[/math],

where [math]\displaystyle{ W^{a\mu\nu} }[/math] ([math]\displaystyle{ a=1,2,3 }[/math]) and [math]\displaystyle{ B^{\mu\nu} }[/math] are the field strength tensors for the weak isospin and weak hypercharge gauge fields.

[math]\displaystyle{ \mathcal{L}_f }[/math] is the kinetic term for the Standard Model fermions. The interaction of the gauge bosons and the fermions are through the gauge covariant derivative,

[math]\displaystyle{ \mathcal{L}_f = \overline{Q}_j iD\!\!\!\!/\; Q_j+ \overline{u}_j iD\!\!\!\!/\; u_j+ \overline{d}_j iD\!\!\!\!/\; d_j + \overline{L}_j iD\!\!\!\!/\; L_j + \overline{e}_j iD\!\!\!\!/\; e_j }[/math],

where the subscript j sums over the three generations of fermions; Q, u, and d are the left-handed doublet, right-handed singlet up, and right handed singlet down quark fields; and L and e are the left-handed doublet and right-handed singlet electron fields. The Feynman slash [math]\displaystyle{ D\!\!\!\!/ }[/math] means the contraction of the 4-gradient with the Dirac matrices, defined as

[math]\displaystyle{ D\!\!\!\!/ \equiv \gamma^\mu\ D_\mu }[/math]

and the covariant derivative (excluding the gluon gauge field for the strong interaction) is defined as

[math]\displaystyle{ \ D_\mu \equiv \partial_\mu - i\ \frac{g'}{2}\ Y\ B_\mu - i\ \frac{g}{2}\ T_j\ W_\mu^j }[/math]

Here [math]\displaystyle{ \ Y\ }[/math] is the weak hypercharge and the [math]\displaystyle{ \ T_j\ }[/math] are the components of the weak isospin.

The [math]\displaystyle{ \mathcal{L}_h }[/math] term describes the Higgs field [math]\displaystyle{ h }[/math] and its interactions with itself and the gauge bosons,

[math]\displaystyle{ \mathcal{L}_h = |D_\mu h|^2 - \lambda \left(|h|^2 - \frac{v^2}{2}\right)^2\ , }[/math]

where [math]\displaystyle{ v }[/math] is the vacuum expectation value.

The [math]\displaystyle{ \ \mathcal{L}_y\ }[/math] term describes the Yukawa interaction with the fermions,

[math]\displaystyle{ \mathcal{L}_y = - y_{u\ ij}\epsilon^{ab}\ h_b^\dagger\ \overline{Q}_{ia} u_j^c - y_{d\ ij}\ h\ \overline{Q}_i d^c_j - y_{e\,ij}\ h\ \overline{L}_i e^c_j + \mathrm{h.c.} ~, }[/math]

and generates their masses, manifest when the Higgs field acquires a nonzero vacuum expectation value, discussed next. The [math]\displaystyle{ \ y_k^{ij}\ , }[/math] for [math]\displaystyle{ \ k \in \{ \mathrm{u, d, e} \}\ , }[/math] are matrices of Yukawa couplings.

After electroweak symmetry breaking

The Lagrangian reorganizes itself as the Higgs boson acquires a non-vanishing vacuum expectation value dictated by the potential of the previous section. As a result of this rewriting, the symmetry breaking becomes manifest. In the history of the universe, this is believed to have happened shortly after the hot big bang, when the universe was at a temperature 159.5±1.5 GeV (assuming the Standard Model of particle physics).

Due to its complexity, this Lagrangian is best described by breaking it up into several parts as follows.

[math]\displaystyle{ \mathcal{L}_{\mathrm{EW}} = \mathcal{L}_\mathrm{K} + \mathcal{L}_\mathrm{N} + \mathcal{L}_\mathrm{C} + \mathcal{L}_\mathrm{H} + \mathcal{L}_{\mathrm{HV}} + \mathcal{L}_{\mathrm{WWV}} + \mathcal{L}_{\mathrm{WWVV}} + \mathcal{L}_\mathrm{Y} ~. }[/math]

The kinetic term [math]\displaystyle{ \mathcal{L}_K }[/math] contains all the quadratic terms of the Lagrangian, which include the dynamic terms (the partial derivatives) and the mass terms (conspicuously absent from the Lagrangian before symmetry breaking)

[math]\displaystyle{ \begin{align} \mathcal{L}_\mathrm{K} = \sum_f \overline{f}(i\partial\!\!\!/\!\;-m_f)\ f - \frac{1}{4}\ A_{\mu\nu}\ A^{\mu\nu} - \frac{1}{2}\ W^+_{\mu\nu}\ W^{-\mu\nu} + m_W^2\ W^+_\mu\ W^{-\mu} \\ \qquad -\frac{1}{4}\ Z_{\mu\nu}Z^{\mu\nu} + \frac{1}{2}\ m_Z^2\ Z_\mu\ Z^\mu + \frac{1}{2}\ (\partial^\mu\ H)(\partial_\mu\ H) - \frac{1}{2}\ m_H^2\ H^2 ~, \end{align} }[/math]

where the sum runs over all the fermions of the theory (quarks and leptons), and the fields [math]\displaystyle{ \ A_{\mu\nu}\ , }[/math] [math]\displaystyle{ \ Z_{\mu\nu}\ , }[/math] [math]\displaystyle{ \ W^-_{\mu\nu}\ , }[/math] and [math]\displaystyle{ \ W^+_{\mu\nu} \equiv (W^-_{\mu\nu})^\dagger\ }[/math] are given as

[math]\displaystyle{ X^{a}_{\mu\nu} = \partial_\mu X^{a}_\nu - \partial_\nu X^{a}_\mu + g f^{abc}X^{b}_{\mu}X^{c}_{\nu} ~, }[/math]

with '[math]\displaystyle{ X }[/math]' to be replaced by the relevant field ([math]\displaystyle{ A }[/math], [math]\displaystyle{ Z }[/math], [math]\displaystyle{ W^\pm }[/math]), and f ^abc by the structure constants of the appropriate gauge group.

The neutral current [math]\displaystyle{ \ \mathcal{L}_\mathrm{N}\ }[/math] and charged current [math]\displaystyle{ \ \mathcal{L}_\mathrm{C}\ }[/math] components of the Lagrangian contain the interactions between the fermions and gauge bosons,

[math]\displaystyle{ \mathcal{L}_\mathrm{N} = e\ J_\mu^\mathrm{em}\ A^\mu + \frac{g}{\ \cos\theta_W\ }\ (\ J_\mu^3 - \sin^2\theta_W\ J_\mu^\mathrm{em}\ )\ Z^\mu ~, }[/math]

where [math]\displaystyle{ ~e = g\ \sin \theta_\mathrm{W} = g'\ \cos \theta_\mathrm{W} ~. }[/math] The electromagnetic current [math]\displaystyle{ \; J_\mu^{\mathrm{em}} \; }[/math] is

[math]\displaystyle{ J_\mu^\mathrm{em} = \sum_f \ q_f\ \overline{f}\ \gamma_\mu\ f ~, }[/math]

where [math]\displaystyle{ \ q_f\ }[/math] is the fermions' electric charges. The neutral weak current [math]\displaystyle{ \ J_\mu^3\ }[/math] is

[math]\displaystyle{ J_\mu^3 = \sum_f\ T^3_f\ \overline{f}\ \gamma_\mu\ \frac{\ 1-\gamma^5\ }{2}\ f ~, }[/math]

where [math]\displaystyle{ T^3_f }[/math] is the fermions' weak isospin.

The charged current part of the Lagrangian is given by

[math]\displaystyle{ \mathcal{L}_\mathrm{C} = -\frac{g}{\ \sqrt{2 \;}\ }\ \left[\ \overline{u}_i\ \gamma^\mu\ \frac{\ 1 - \gamma^5\ }{2} \; M^{\mathrm{CKM}}_{ij}\ d_j + \overline{\nu}_i\ \gamma^\mu\;\frac{\ 1-\gamma^5\ }{2} \; e_i\ \right]\ W_\mu^{+} + \mathrm{h.c.} ~, }[/math]

where [math]\displaystyle{ \ \nu\ }[/math] is the right-handed singlet neutrino field, and the CKM matrix [math]\displaystyle{ \ M_{ij}^\mathrm{CKM}\ }[/math] determines the mixing between mass and weak eigenstates of the quarks.

[math]\displaystyle{ \mathcal{L}_\mathrm{H} }[/math] contains the Higgs three-point and four-point self interaction terms,

[math]\displaystyle{ \mathcal{L}_\mathrm{H} = -\frac{\ g\ m_\mathrm{H}^2\,}{\ 4\ m_\mathrm{W}\ }\;H^3 - \frac{\ g^2\ m_\mathrm{H}^2\ }{32\ m_\mathrm{W}^2}\;H^4 ~. }[/math]

[math]\displaystyle{ \mathcal{L}_{\mathrm{HV}} }[/math] contains the Higgs interactions with gauge vector bosons,

[math]\displaystyle{ \mathcal{L}_\mathrm{HV} =\left(\ g\ m_\mathrm{HV} + \frac{\ g^2\ }{4}\;H^2\ \right)\left(\ W^{+}_\mu\ W^{-\mu} + \frac{1}{\ 2\ \cos^2\ \theta_\mathrm{W}\ }\;Z_\mu\ Z^\mu\ \right) ~. }[/math]

[math]\displaystyle{ \ \mathcal{L}_{\mathrm{WWV}}\ }[/math] contains the gauge three-point self interactions,

[math]\displaystyle{ \mathcal{L}_{\mathrm{WWV}} = -i\ g\ \left[\; \left(\ W_{\mu\nu}^{+}\ W^{-\mu} - W^{+\mu}\ W^{-}_{\mu\nu}\ \right)\left(\ A^\nu\ \sin \theta_\mathrm{W} - Z^\nu\ \cos\theta_\mathrm{W}\ \right) + W^{-}_\nu\ W^{+}_\mu\ \left(\ A^{\mu\nu}\ \sin \theta_\mathrm{W} - Z^{\mu\nu}\ \cos \theta_\mathrm{W}\ \right) \;\right] ~. }[/math]

[math]\displaystyle{ \ \mathcal{L}_{\mathrm{WWVV}}\ }[/math] contains the gauge four-point self interactions,

[math]\displaystyle{ \begin{align} \mathcal{L}_{\mathrm{WWVV}} = -\frac{\ g^2\ }{4}\ \Biggl\{\ &\Bigl[\ 2\ W^{+}_\mu\ W^{-\mu} + (\ A_\mu\ \sin \theta_\mathrm{W} - Z_\mu\ \cos \theta_\mathrm{W} \ )^2\ \Bigr]^2 \\ &- \Bigl[\ W_\mu^{+}\ W_\nu^{-} + W^{+}_\nu\ W^{-}_\mu + \left(\ A_\mu\ \sin \theta_\mathrm{W} - Z_\mu\ \cos \theta_\mathrm{W}\ \right)\left(\ A_\nu\ \sin \theta_\mathrm{W} - Z_\nu\ \cos \theta_\mathrm{W}\ \right)\ \Bigr]^2\,\Biggr\} ~. \end{align} }[/math]

[math]\displaystyle{ \ \mathcal{L}_\mathrm{Y}\ }[/math] contains the Yukawa interactions between the fermions and the Higgs field,

[math]\displaystyle{ \mathcal{L}_\mathrm{Y} = -\sum_f\ \frac{\ g\ m_f\ }{2\ m_\mathrm{W}} \; \overline{f}\ f\ H ~. }[/math]

See also

• Electroweak star
• Fundamental forces
• History of quantum field theory
• Standard Model (mathematical formulation)
• Unitarity gauge
• Weinberg angle
• Yang–Mills theory

Further reading

General readers

• B. A. Schumm (2004). Deep Down Things: The Breathtaking Beauty of Particle Physics. Johns Hopkins University Press. ISBN 0-8018-7971-X. https://archive.org/details/deepdownthingsbr00schu.  Conveys much of the Standard Model with no formal mathematics. Very thorough on the weak interaction.

Texts

• D. J. Griffiths (1987). Introduction to Elementary Particles. John Wiley & Sons. ISBN 0-471-60386-4. 
• W. Greiner; B. Müller (2000). Gauge Theory of Weak Interactions. Springer. ISBN 3-540-67672-4. 
• G. L. Kane (1987). Modern Elementary Particle Physics. Perseus Books. ISBN 0-201-11749-5. 

Articles

• E. S. Abers; B. W. Lee (1973). "Gauge theories". Physics Reports 9 (1): 1–141. doi:10.1016/0370-1573(73)90027-6. Bibcode: 1973PhR.....9....1A. 
• Y. Hayato (1999). "Search for Proton Decay through p → νK⁺ in a Large Water Cherenkov Detector". Physical Review Letters 83 (8): 1529–1533. doi:10.1103/PhysRevLett.83.1529. Bibcode: 1999PhRvL..83.1529H. 
• J. Hucks (1991). "Global structure of the standard model, anomalies, and charge quantization". Physical Review D 43 (8): 2709–2717. doi:10.1103/PhysRevD.43.2709. PMID 10013661. Bibcode: 1991PhRvD..43.2709H. 
• S. F. Novaes (2000). "Standard Model: An Introduction". arXiv:hep-ph/0001283.
• D. P. Roy (1999). "Basic Constituents of Matter and their Interactions – A Progress Report". arXiv:hep-ph/9912523.