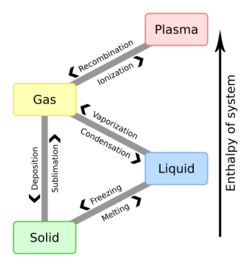
Physics:Melting point

From HandWiki
Short description: Temperature at which a solid turns liquid
Ice cubes put in water will start to melt when they reach their melting point of 0 °C

The melting point (or, rarely, liquefaction point) of a substance is the temperature at which it changes state from solid to liquid. At the melting point the solid and liquid phase exist in equilibrium. The melting point of a substance depends on pressure and is usually specified at a standard pressure such as 1 atmosphere or 100 kPa.

When considered as the temperature of the reverse change from liquid to solid, it is referred to as the freezing point or crystallization point. Because of the ability of substances to supercool, the freezing point can easily appear to be below its actual value. When the "characteristic freezing point" of a substance is determined, in fact, the actual methodology is almost always "the principle of observing the disappearance rather than the formation of ice, that is, the melting point."[1]

Examples

Melting points (in blue) and boiling points (in pink) of the first eight carboxylic acids (°C)

For most substances, melting and freezing points are approximately equal. For example, the melting and freezing points of mercury is 234.32 kelvins (−38.83 °C; −37.89 °F).[2] However, certain substances possess differing solid-liquid transition temperatures. For example, agar melts at 85 °C (185 °F; 358 K) and solidifies from 31 °C (88 °F; 304 K); such direction dependence is known as hysteresis. The melting point of ice at 1 atmosphere of pressure is very close[3] to 0 °C (32 °F; 273 K); this is also known as the ice point. In the presence of nucleating substances, the freezing point of water is not always the same as the melting point. In the absence of nucleators water can exist as a supercooled liquid down to −48.3 °C (−54.9 °F; 224.8 K) before freezing.[citation needed]

The metal with the highest melting point is tungsten, at 3,414 °C (6,177 °F; 3,687 K);[4] this property makes tungsten excellent for use as electrical filaments in incandescent lamps. The often-cited carbon does not melt at ambient pressure but sublimes at about 3,700 °C (6,700 °F; 4,000 K); a liquid phase only exists above pressures of 10 MPa (99 atm) and estimated 4,030–4,430 °C (7,290–8,010 °F; 4,300–4,700 K) (see carbon phase diagram). Hafnium carbonitride (HfCN) is a refractory compound with the highest known melting point of any substance to date and the only one confirmed to have a melting point above 4,273 K (4,000 °C; 7,232 °F) at ambient pressure. Quantum mechanical computer simulations predicted that this alloy (HfN0.38C0.51) would have a melting point of about 4,400 K.[5] This prediction was later confirmed by experiment, though a precise measurement of its exact melting point has yet to be confirmed.[6] At the other end of the scale, helium does not freeze at all at normal pressure even at temperatures arbitrarily close to absolute zero; a pressure of more than twenty times normal atmospheric pressure is necessary.

List of common chemicals
Chemical[upper-roman 1] Density (g/cm3) Melt (K)[7] Boil (K)
Water @STP 1 273 373
Solder (Pb60Sn40) 461
Cocoa butter 307.2 -
Paraffin wax 0.9 310 643
Hydrogen 0.00008988 0014 14.01 20.28
Helium 0.0001785 0.1 —

[upper-roman 2] || 4.22

Beryllium 1.85 1560 1,560 2,742
Carbon 2.267 0.1 —

[upper-roman 3][8] || 4,000[upper-roman 3][8]

Nitrogen 0.0012506 0063 63.15 77.36
Oxygen 0.001429 0054 54.36 90.20
Sodium 0.971 0371 370.87 1,156
Magnesium 1.738 0923 923 1,363
Aluminium 2.698 0933.5 933.47 2,792
Sulfur 2.067 0388.4 388.36 717.87
Chlorine 0.003214 0171.6 171.6 239.11
Potassium 0.862 0336.5 336.53 1,032
Titanium 4.54 1941 1,941 3,560
Iron 7.874 1811 1,811 3,134
Nickel 8.912 1728 1,728 3,186
Copper 8.96 1,357.77 2,835
Zinc 7.134 0693 692.88 1,180
Gallium 5.907 0302.9 302.9146 2,673
Silver 10.501 1,234.93 2,435
Cadmium 8.69 0594.22 594.22 1,040
Indium 7.31 0429.75 429.75 2,345
Iodine 4.93 0386.85 386.85 457.4
Tantalum 16.654 3,290 5,731
Tungsten 19.25 3,695 5,828
Platinum 21.46 2,041.4 4,098
Gold 19.282 1,337.33 3,129
Mercury 13.5336 0234.43 234.43 629.88
Lead 11.342 0600.61 600.61 2,022
Bismuth 9.807 0544.7 544.7 1,837

Notes

  1. ↑ Z is the standard symbol for atomic number; C is the standard symbol for heat capacity; and χ is the standard symbol for electronegativity on the Pauling scale.
  2. ↑ Helium does not solidify at a pressure of one atmosphere. Helium can only solidify at pressures above 25 atmospheres, which corresponds to a melting point of absolute zero.
  3. ↑ 3.0 3.1 Carbon does not melt at any temperature under standard pressure, instead it sublimes around 4,100 K

Melting point measurements

Main page: Engineering:Melting-point apparatus
Kofler bench with samples for calibration

Many laboratory techniques exist for the determination of melting points. A Kofler bench is a metal strip with a temperature gradient (range from room temperature to 300 °C). Any substance can be placed on a section of the strip, revealing its thermal behaviour at the temperature at that point. Differential scanning calorimetry gives information on melting point together with its enthalpy of fusion.

Automatic digital melting point meter

A basic melting point apparatus for the analysis of crystalline solids consists of an oil bath with a transparent window (most basic design: a Thiele tube) and a simple magnifier. Several grains of a solid are placed in a thin glass tube and partially immersed in the oil bath. The oil bath is heated (and stirred) and with the aid of the magnifier (and external light source) melting of the individual crystals at a certain temperature can be observed. A metal block might be used instead of an oil bath. Some modern instruments have automatic optical detection.

The measurement can also be made continuously with an operating process. For instance, oil refineries measure the freeze point of diesel fuel "online", meaning that the sample is taken from the process and measured automatically. This allows for more frequent measurements as the sample does not have to be manually collected and taken to a remote laboratory.[citation needed]

Techniques for refractory materials

For refractory materials (e.g. platinum, tungsten, tantalum, some carbides and nitrides, etc.) the extremely high melting point (typically considered to be above, say, 1,800 °C) may be determined by heating the material in a black body furnace and measuring the black-body temperature with an optical pyrometer. For the highest melting materials, this may require extrapolation by several hundred degrees. The spectral radiance from an incandescent body is known to be a function of its temperature. An optical pyrometer matches the radiance of a body under study to the radiance of a source that has been previously calibrated as a function of temperature. In this way, the measurement of the absolute magnitude of the intensity of radiation is unnecessary. However, known temperatures must be used to determine the calibration of the pyrometer. For temperatures above the calibration range of the source, an extrapolation technique must be employed. This extrapolation is accomplished by using Planck's law of radiation. The constants in this equation are not known with sufficient accuracy, causing errors in the extrapolation to become larger at higher temperatures. However, standard techniques have been developed to perform this extrapolation.[citation needed]

Consider the case of using gold as the source (mp = 1,063 °C). In this technique, the current through the filament of the pyrometer is adjusted until the light intensity of the filament matches that of a black-body at the melting point of gold. This establishes the primary calibration temperature and can be expressed in terms of current through the pyrometer lamp. With the same current setting, the pyrometer is sighted on another black-body at a higher temperature. An absorbing medium of known transmission is inserted between the pyrometer and this black-body. The temperature of the black-body is then adjusted until a match exists between its intensity and that of the pyrometer filament. The true higher temperature of the black-body is then determined from Planck's Law. The absorbing medium is then removed and the current through the filament is adjusted to match the filament intensity to that of the black-body. This establishes a second calibration point for the pyrometer. This step is repeated to carry the calibration to higher temperatures. Now, temperatures and their corresponding pyrometer filament currents are known and a curve of temperature versus current can be drawn. This curve can then be extrapolated to very high temperatures.

In determining melting points of a refractory substance by this method, it is necessary to either have black body conditions or to know the emissivity of the material being measured. The containment of the high melting material in the liquid state may introduce experimental difficulties. Melting temperatures of some refractory metals have thus been measured by observing the radiation from a black body cavity in solid metal specimens that were much longer than they were wide. To form such a cavity, a hole is drilled perpendicular to the long axis at the center of a rod of the material. These rods are then heated by passing a very large current through them, and the radiation emitted from the hole is observed with an optical pyrometer. The point of melting is indicated by the darkening of the hole when the liquid phase appears, destroying the black body conditions. Today, containerless laser heating techniques, combined with fast pyrometers and spectro-pyrometers, are employed to allow for precise control of the time for which the sample is kept at extreme temperatures. Such experiments of sub-second duration address several of the challenges associated with more traditional melting point measurements made at very high temperatures, such as sample vaporization and reaction with the container.

Thermodynamics

Pressure dependence of water melting point.

For a solid to melt, heat is required to raise its temperature to the melting point. However, further heat needs to be supplied for the melting to take place: this is called the heat of fusion, and is an example of latent heat.[citation needed]

From a thermodynamics point of view, at the melting point the change in Gibbs free energy (ΔG) of the material is zero, but the enthalpy (H) and the entropy (S) of the material are increasing (ΔH, ΔS > 0). Melting phenomenon happens when the Gibbs free energy of the liquid becomes lower than the solid for that material. At various pressures this happens at a specific temperature. It can also be shown that:

[math]\displaystyle{ \Delta S = \frac {\Delta H} {T} }[/math]

Here T, ΔS and ΔH are respectively the temperature at the melting point, change of entropy of melting and the change of enthalpy of melting.

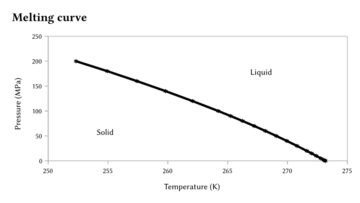
The melting point is sensitive to extremely large changes in pressure, but generally this sensitivity is orders of magnitude less than that for the boiling point, because the solid-liquid transition represents only a small change in volume.[9][10] If, as observed in most cases, a substance is more dense in the solid than in the liquid state, the melting point will increase with increases in pressure. Otherwise the reverse behavior occurs. Notably, this is the case of water, as illustrated graphically to the right, but also of Si, Ge, Ga, Bi. With extremely large changes in pressure, substantial changes to the melting point are observed. For example, the melting point of silicon at ambient pressure (0.1 MPa) is 1415 °C, but at pressures in excess of 10 GPa it decreases to 1000 °C.[11]

Melting points are often used to characterize organic and inorganic compounds and to ascertain their purity. The melting point of a pure substance is always higher and has a smaller range than the melting point of an impure substance or, more generally, of mixtures. The higher the quantity of other components, the lower the melting point and the broader will be the melting point range, often referred to as the "pasty range". The temperature at which melting begins for a mixture is known as the solidus while the temperature where melting is complete is called the liquidus. Eutectics are special types of mixtures that behave like single phases. They melt sharply at a constant temperature to form a liquid of the same composition. Alternatively, on cooling a liquid with the eutectic composition will solidify as uniformly dispersed, small (fine-grained) mixed crystals with the same composition.

In contrast to crystalline solids, glasses do not possess a melting point; on heating they undergo a smooth glass transition into a viscous liquid. Upon further heating, they gradually soften, which can be characterized by certain softening points.

Freezing-point depression

Main pages: Chemistry:Freezing-point depression and Physics:Supercooling

The freezing point of a solvent is depressed when another compound is added, meaning that a solution has a lower freezing point than a pure solvent. This phenomenon is used in technical applications to avoid freezing, for instance by adding salt or ethylene glycol to water.[citation needed]

Carnelley's rule

In organic chemistry, Carnelley's rule, established in 1882 by Thomas Carnelley, states that high molecular symmetry is associated with high melting point.[12] Carnelley based his rule on examination of 15,000 chemical compounds. For example, for three structural isomers with molecular formula C5H12 the melting point increases in the series isopentane −160 °C (113 K) n-pentane −129.8 °C (143 K) and neopentane −16.4 °C (256.8 K).[13] Likewise in xylenes and also dichlorobenzenes the melting point increases in the order meta, ortho and then para. Pyridine has a lower symmetry than benzene hence its lower melting point but the melting point again increases with diazine and triazines. Many cage-like compounds like adamantane and cubane with high symmetry have relatively high melting points.

A high melting point results from a high heat of fusion, a low entropy of fusion, or a combination of both. In highly symmetrical molecules the crystal phase is densely packed with many efficient intermolecular interactions resulting in a higher enthalpy change on melting. thumb|right|180 px|Like many high symmetry compounds, [[tetrakis(trimethylsilyl)silane has a very high melting point (m.p.) of 319-321 °C. It tends to sublime, so the m.p. determination requires that the sample be sealed in a tube.[14]]]

Predicting the melting point of substances (Lindemann's criterion)

An attempt to predict the bulk melting point of crystalline materials was first made in 1910 by Frederick Lindemann.[15] The idea behind the theory was the observation that the average amplitude of thermal vibrations increases with increasing temperature. Melting initiates when the amplitude of vibration becomes large enough for adjacent atoms to partly occupy the same space. The Lindemann criterion states that melting is expected when the vibration root mean square amplitude exceeds a threshold value.

Assuming that all atoms in a crystal vibrate with the same frequency ν, the average thermal energy can be estimated using the equipartition theorem as[16]

[math]\displaystyle{ E = 4\pi^2 m \nu^2~u^2 = k_{\rm B} T }[/math]

where m is the atomic mass, ν is the frequency, u is the average vibration amplitude, kB is the Boltzmann constant, and T is the absolute temperature. If the threshold value of u2 is c2a2 where c is the Lindemann constant and a is the atomic spacing, then the melting point is estimated as

[math]\displaystyle{ T_{\rm m} = \cfrac{4\pi^2 m \nu^2 c^2 a^2}{k_{\rm B}} . }[/math]

Several other expressions for the estimated melting temperature can be obtained depending on the estimate of the average thermal energy. Another commonly used expression for the Lindemann criterion is[17]

[math]\displaystyle{ T_{\rm m} = \cfrac{4\pi^2 m \nu^2 c^2 a^2}{2k_{\rm B}} . }[/math]

From the expression for the Debye frequency for ν,

[math]\displaystyle{ T_{\rm m} = \cfrac{2\pi m c^2 a^2 \theta_{\rm D}^2 k_{\rm B}}{h^2} }[/math]

where θD is the Debye temperature and h is the Planck constant. Values of c range from 0.15 to 0.3 for most materials.[18]

Melting point prediction

In February 2011, Alfa Aesar released over 10,000 melting points of compounds from their catalog as open data. This dataset has been used to create a random forest model for melting point prediction which is now freely available.[19] Open melting point data are also available from Nature Precedings.[20] High quality data mined from patents and also models[21] developed with these data were published by Tetko et al.[22]

Melting point of the elements

Main page: Chemistry:Melting points of the elements (data page)

See also


References

Citations

  1. ↑ Ramsay, J. A. (1 May 1949). "A New Method of Freezing-Point Determination for Small Quantities". Journal of Experimental Biology 26 (1): 57–64. doi:10.1242/jeb.26.1.57. PMID 15406812. http://jeb.biologists.org/cgi/pmidlookup?view=long&pmid=15406812. 
  2. ↑ Haynes, p. 4.122.
  3. ↑ The melting point of purified water has been measured as 0.002519 ± 0.000002 °C, see Feistel, R.; Wagner, W. (2006). "A New Equation of State for H2O Ice Ih". Journal of Physical and Chemical Reference Data 35 (2): 1021–1047. doi:10.1063/1.2183324. Bibcode: 2006JPCRD..35.1021F. 
  4. ↑ Haynes, p. 4.123.
  5. ↑ Hong, Q.-J.; van de Walle, A. (2015). "Prediction of the material with highest known melting point from ab initio molecular dynamics calculations". Phys. Rev. B 92 (2): 020104(R). doi:10.1103/PhysRevB.92.020104. Bibcode: 2015PhRvB..92b0104H. 
  6. ↑ Buinevich, V.S.; Nepapushev, A.A.; Moskovskikh, D.O.; Trusov, G.V.; Kuskov, K.V.; Vadchenko, S.G.; Rogachev, A.S.; Mukasyan, A.S. (March 2020). "Fabrication of ultra-high-temperature nonstoichiometric hafnium carbonitride via combustion synthesis and spark plasma sintering". Ceramics International 46 (10): 16068–16073. doi:10.1016/j.ceramint.2020.03.158. 
  7. ↑ Holman, S. W.; Lawrence, R. R.; Barr, L. (1 January 1895). "Melting Points of Aluminum, Silver, Gold, Copper, and Platinum". Proceedings of the American Academy of Arts and Sciences 31: 218–233. doi:10.2307/20020628. 
  8. ↑ 8.0 8.1 "Carbon". https://www.rsc.org/periodic-table/element/6/carbon. 
  9. ↑ The exact relationship is expressed in the Clausius–Clapeyron relation.
  10. ↑ "J10 Heat: Change of aggregate state of substances through change of heat content: Change of aggregate state of substances and the equation of Clapeyron-Clausius". http://mpec.sc.mahidol.ac.th/RADOK/physmath/PHYSICS/j10.htm. 
  11. ↑ Tonkov, E. Yu. and Ponyatovsky, E. G. (2005) Phase Transformations of Elements Under High Pressure, CRC Press, Boca Raton, p. 98 ISBN:0-8493-3367-9
  12. ↑ Brown, R. J. C.; R. F. C. (2000). "Melting Point and Molecular Symmetry". Journal of Chemical Education 77 (6): 724. doi:10.1021/ed077p724. Bibcode: 2000JChEd..77..724B. 
  13. ↑ Haynes, pp. 6.153–155.
  14. ↑ Gilman, H.; Smith, C. L. (1967). "Tetrakis(trimethylsilyl)silane". Journal of Organometallic Chemistry 8 (2): 245–253. doi:10.1016/S0022-328X(00)91037-4. 
  15. ↑ Lindemann FA (1910). "The calculation of molecular vibration frequencies". Phys. Z. 11: 609–612. 
  16. ↑ Sorkin, S., (2003), Point defects, lattice structure, and melting , Thesis, Technion, Israel.
  17. ↑ Philip Hofmann (2008). Solid state physics: an introduction. Wiley-VCH. p. 67. ISBN 978-3-527-40861-0. https://books.google.com/books?id=XfIpxi4kcM4C&pg=PA67. Retrieved 13 March 2011. [yes|permanent dead link|dead link}}]
  18. ↑ Nelson, D. R., (2002), Defects and geometry in condensed matter physics, Cambridge University Press, ISBN:0-521-00400-4
  19. ↑ Predict melting point from SMILES. Qsardb.org. Retrieved on 13 September 2013.
  20. ↑ Bradley, Jean-Claude; Lang, Andrew; Williams, Antony; Curtin, Evan (11 August 2011). "ONS Open Melting Point Collection". Nature Precedings. doi:10.1038/npre.2011.6229.1. 
  21. ↑ OCHEM melting point models. ochem.eu. Retrieved on 18 June 2016.
  22. ↑ Tetko, Igor V; m. Lowe, Daniel; Williams, Antony J (2016). "The development of models to predict melting and pyrolysis point data associated with several hundred thousand compounds mined from PATENTS". Journal of Cheminformatics 8: 2. doi:10.1186/s13321-016-0113-y. PMID 26807157. 

Sources

Works cited
  • Haynes, William M., ed (2011). CRC Handbook of Chemistry and Physics (92nd ed.). CRC Press. ISBN 978-1439855119. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Melting_point&oldid=3285522"