Elitzur–Vaidman bomb tester

Short description: Quantum mechanics thought experiment

Bomb-testing problem diagram. A – photon emitter, B – bomb to be tested, C, D – photon detectors. Mirrors in the lower left and upper right corners are semi-transparent.

The Elitzur–Vaidman bomb-tester is a quantum mechanics thought experiment that uses interaction-free measurements to verify that a bomb is functional without having to detonate it. It was conceived in 1993 by Avshalom Elitzur and Lev Vaidman. Since their publication, real-world experiments have confirmed that their theoretical method works as predicted.^[1]

The bomb tester takes advantage of two characteristics of elementary particles, such as photons or electrons: nonlocality and wave–particle duality.^[2] By placing the particle in a quantum superposition, it is possible for the experiment to verify that the bomb works without triggering its detonation, although there is still a 50% chance that the bomb will detonate in the effort.

Background

The bomb test is an interaction-free measurement. The idea of getting information about an object without interacting with it is not a new one. For example, there are two boxes, one of which contains something, the other of which contains nothing. If you open one box and see nothing, you know that the other contains something, without ever opening it.^[2]

This experiment has its roots in the double-slit experiment and other, more complex concepts which inspired it, including Schrödinger's cat, and Wheeler's delayed-choice experiment.^[3] The behavior of elementary particles is very different from what we experience in our macroscopic world. Their observed behavior can be that of a wave or of a particle (see wave–particle duality), their wave-like behavior implies what is called "superposition". In this state, some properties of the particle, for example, its location, are not definite. While in a superposition, any and all possibilities are equally real. So, if the particle could feasibly exist in more than one location, in certain senses that are experimentally useful, it exists in all of them simultaneously. The particle's wave can later be "collapsed" by observing it, at which time its location (or other measured property) at the moment of observation is definite. Information can then be gleaned not only about the actual state of the particle, but also other states or locations in which it "existed" before the collapse. This gleaning of information is possible even if the particle was never factually in any of the particular states or locations that are of interest.

How it works

Figure 1: An illustration of the experiment using a Mach–Zehnder interferometer

Figure 2: Legend for Fig. 1

Consider a collection of light-sensitive bombs, of which some are duds. When their triggers detect any light, even a single photon, the light is absorbed and the bomb explodes. The triggers on the dud bombs have no sensor, so any light incident on the bomb will not be absorbed and will instead pass straight through.^[4] The dud bomb will not detect any photon and will not detonate. Is it possible to determine which bombs are functional and which are duds without detonating all of the live ones?

Components

A light-sensitive bomb: it is not known whether it is live or a dud.
A photon emitter: it produces a single photon for the purposes of the experiment.
A photon: after being emitted, it travels through the box below.
A "box" which contains:
- An initial half-silvered mirror: the photon enters the box when it encounters this "beam splitter". The photon will either pass through the mirror and travel along the "lower path" inside the box, or be reflected at a 90-degree angle and travel along the box's "upper path".
- The bomb in question: the bomb is placed inside the box beforehand on the "lower path". If the bomb is live and comes into contact with a photon, it will detonate and destroy itself and the photon. If, however, the bomb is a dud, the photon passes it by and continues on its way along the lower path.
- A pair of ordinary mirrors: one mirror is located on each beam path. They are positioned to redirect the photon so that the two paths intersect one another at the same position as the second beam splitter.
- A second beam splitter: identical to the initial one. This beam splitter is positioned opposite the first, at the intersection between the lower path and upper path (after they have been redirected by the ordinary mirrors), at the exit of the box.
A pair of photon detectors: located outside the box, they are aligned with the second beam-splitter. The photon can be detected at either or neither, but never both.

Part 1: The superposition

Figure 3: Once the photon encounters the beam splitter it enters a superposition wherein it both passes through and reflects off the half-silvered mirror

A superposition in the bomb tester is created with an angled half-silvered mirror, which allows a photon to either pass through it, or be reflected off it at a 90-degree angle (see figure 3). There is equal probability it will do either. The photon enters a superposition, in which it does both. The single particle both passes through, and is reflected off the half-silvered mirror. From that moment on, the single photon exists in two different locations.

Along both the upper and lower path, the particle will encounter an ordinary mirror, positioned to redirect the two routes toward one another. They then intersect at a second half-silvered mirror. On the other side, a pair of detectors are placed such that the photon can be detected by either detector, but never by both. It is also possible that it will not be detected by either. Based on this outcome, with a live bomb, there is a 50% chance it will explode, a 25% chance it will be identified as good without exploding and a 25% chance there will be no result.

Part 2: The bomb

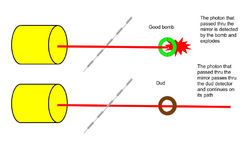
Figure 4: If the bomb is live, it will absorb the photon and detonate. If it is a dud, the photon is unaffected and continues along the lower path.

Figure 5 As in Figure 4, the photon travels the lower path toward the bomb, but in a superposition, where it also travels the upper path.

A light-sensitive bomb is placed along the lower path. If the bomb is live, when a photon arrives, it will explode and both will be destroyed. If it is a dud, the photon will pass by unaffected (see figure 4), i.e., it will remain in superposition until it reaches a detector. To understand how this experiment works, it is important to know that unlike a dud, a live bomb is a kind of observer and that an encounter between the photon and a live bomb is a kind of observation. It can therefore collapse the photon's superposition, in which the photon is travelling along both the upper and lower paths. When it reaches the live bomb, or the detectors, however, it can only have been on one or the other. But, like the radioactive material in the box with Schrödinger's famous cat, upon its encounter with the half-silvered mirror at the beginning of the experiment, the photon, paradoxically does and does not interact with the bomb. According to the authors, the bomb both explodes and does not explode.^[5] This is only in the case of a live bomb, however. In any event, once observed by the detectors, it will have only traveled one of the paths.

Part 3: The second half-silvered mirror

Figure 6: The second half-silvered mirror and the two detectors are positioned so that the photon will only arrive at Detector C if there is wave interference. This is only possible if the bomb is a dud.

When two waves collide, the process by which they affect each other is called interference. They can either strengthen each other by "constructive interference", or weaken each other by "destructive interference".^[6] This is true whether the wave is in water, or a single photon in a superposition. So even though there is only one photon in the experiment, because of its encounter with the first half-silvered mirror, it acts like two. When "it" or "they" are reflected off the ordinary mirrors, it will interfere with itself as if it were two different photons. But that is only true if the bomb is a dud. A live bomb will absorb the photon when it explodes and there will be no opportunity for the photon to interfere with itself.

When it reaches the second half-silvered mirror, if the photon in the experiment is behaving like a particle (in other words, if it is not in a superposition), then it has a fifty-fifty chance it will pass through or be reflected and be detected by one or the other detector. But that is only possible if the bomb is live. If the bomb "observed" the photon, it detonated and destroyed the photon on the lower path, therefore only the photon that takes the upper path will be detected, either at Detector C or Detector D.

Part 4: Detectors C and D

Figure 7: If the bomb is live, and the photon took the upper path, there is no chance of interference at the second half-silvered mirror, and so, just as was the case at the first, it has an equal chance of reflecting off it or passing through it and arriving at either detector C or D. This is the only way it can arrive at D, signifying a live (unexploded) bomb.

Detector D is the key to confirming that the bomb is live.

The two detectors and the second half-silvered mirror are precisely aligned with one another. Detector C is positioned to detect the particle if the bomb is a dud and the particle traveled both paths in its superposition and then constructively interfered with itself. Due to the way in which the interferometer is constructed, a photon going through the second mirror from the lower path towards detector D will have a phase shift of half a wavelength compared to a photon being reflected from the upper path towards that same detector, while a photon coming from the upper path and towards detector C would have the same phase as one being reflected from the lower path towards that detector, so if the photon went through both paths, only detector C would be able to detect the photon. Thus, Detector D is able to detect a photon only in the event of a lone photon going through the second mirror (see figure 6). In other words, if the photon is in a superposition at the time it arrives at the second half-silvered mirror, it will always arrive at detector C and never at detector D.

If the bomb is live, there is a 50/50 chance that the photon took the upper path. If it "factually" did so, then it "counter-factually" took the lower path (see figure 7). That counter-factual event destroyed that photon and left only the photon on the upper path to arrive at the second half-silvered mirror. At which point it will, again, have a 50/50 chance of passing through it or being reflected off it, and, subsequently, it will be detected at either of the two detectors with the same probability. This is what makes it possible for the experiment to verify the bomb is live without actually blowing it up.^[7]

In other words, since if the bomb is live there is no possibility of interference between the two paths, a photon will always be detected in either of the two detectors, while if the bomb is a dud there will be interference which can only cause detector C to be activated, so activation of detector D can only occur if the bomb is live, whether the bomb exploded or not.

Results

With a live bomb, there can be three possible outcomes:

No photon was detected (50% chance).
The photon was detected at C (25% chance).
The photon was detected at D (25% chance).

These correspond with the following conditions of the bomb being tested:

No photon was detected: The bomb exploded and destroyed the photon before it could be detected. This is because the photon in fact took the lower path and triggered the bomb, destroying itself in the process. There is a 50% chance that this will be the outcome if the bomb is live.
The photon was detected at C: This will always be the outcome if a bomb is a dud, however, there is a 25% chance that this will be the outcome if the bomb is live. If the bomb is a dud, this is because the photon remained in its superposition until it reached the second half-silvered mirror and constructively interfered with itself. If the bomb is live, this is because the photon in fact took the upper path and passed through the second half-silvered mirror.
The photon was detected at D: The bomb is live but unexploded. That is because the photon in fact took the upper path and reflected off the second half-silvered mirror, something possible only because there was no photon from the lower path with which it could interfere. This is the only way that a photon can ever be detected at D. If this is the outcome, the experiment has successfully verified that the bomb is live despite the fact that the photon never "factually" encountered the bomb itself. There is a 25% chance that this will be the outcome if the bomb is live.^[7]

If the result is 2, the experiment is repeated. If the photon continues to be observed at C and the bomb does not explode, it can eventually be concluded that the bomb is a dud.^[8]

With this process 25% of live bombs can be identified without being detonated, 50% will be detonated and 25% remain uncertain.^[8] By repeating the process with the uncertain ones, the ratio of identified non-detonated live bombs approaches 33% of the initial population of bombs. See § Experiments below for a modified experiment that can identify the live bombs with a yield rate approaching 100%.

Improving probabilities via repetition

The probability of exploding the bomb can be made arbitrarily small by repeating the interaction several times. It can be modelled in a convenient way with the quantum circuit model.^[9]^[10] Assume that a box which potentially contains a bomb is defined to operate on a single probe qubit in the following way:

If there is no bomb, the qubit passes through unaffected.
If there is a bomb, the qubit gets measured:
- If the measurement outcome is $|0⟩$ , the box returns $|0⟩$ .
- If the measurement outcome is $|1⟩$ , the bomb explodes.

The following quantum circuit can be used to test if a bomb is present:

Where:

$B$ is the box/bomb system, which measures the qubit if a bomb is present
[math]\displaystyle{ R_\epsilon }[/math] is the unitary matrix [math]\displaystyle{ \begin{pmatrix} \cos{\epsilon} & -\sin{\epsilon} \\ \sin{\epsilon} & \cos{\epsilon} \end{pmatrix} }[/math]
[math]\displaystyle{ \epsilon = \frac{\pi}{2T} }[/math]
[math]\displaystyle{ T }[/math] is a large integer.

At the end of the circuit, the probe qubit is measured. If the outcome is $|0⟩$ , there is a bomb, and if the outcome is $|1⟩$ , there is no bomb.

Case 1: No bomb

When there is no bomb, the qubit evolves prior to measurement as [math]\displaystyle{ R_\epsilon^T |0\rangle = \cos(T\epsilon) |0\rangle + \sin(T\epsilon) |1 \rangle }[/math], which will measure as $|1⟩$ (the correct answer) with probability [math]\displaystyle{ \sin^2(T\epsilon) = 1 }[/math].

Case 2: Bomb

When there is a bomb, the qubit will be transformed into the state [math]\displaystyle{ \cos(\epsilon) |0\rangle + \sin(\epsilon) |1 \rangle }[/math], then measured by the box. The probability of measuring as $|1⟩$ and exploding is [math]\displaystyle{ \sin^2(\epsilon) \approx \epsilon^2 }[/math] by the small-angle approximation. Otherwise, the qubit will collapse to $|0⟩$ and the circuit will continue iterating.

The probability of obtaining result $|0⟩$ after T iterations, and thus correctly identifying that there is a bomb without exploding it, is given by [math]\displaystyle{ \cos^{2T}(\epsilon) \approx 1 - \frac{\pi^2}{4T} }[/math], which is arbitrarily close to 1. The probability of the bomb having exploded until then is [math]\displaystyle{ 1 - \cos^{2T}(\epsilon) \approx \frac{\pi^2}{4T} }[/math], which is arbitrarily small.

Interpretations

The authors state that the ability to obtain information about the bomb's functionality without ever "touching" it appears to be a paradox that, they argue, is based on the assumption that there is only a single "real" result.^[3] But according to the many-worlds interpretation, each possible state of a particle's superposition is real. The authors therefore argue that the particle does actually interact with the bomb and it does explode, just not in our "world".^[5]

Jean Bricmont offered an interpretation of the Elitzur–Vaidman bomb test in terms of Bohmian mechanics.^[11] It has also been argued that the bomb test can be constructed within the Spekkens toy model, suggesting that it is a less dramatic illustration of non-classicality than other quantum phenomena like the violation of Bell inequalities.^[12] The argument from Spekkens toy model involves the detector being able to detect a photon as either [math]\displaystyle{ |0 \rangle }[/math] and [math]\displaystyle{ |1 \rangle }[/math], where the [math]\displaystyle{ |0 \rangle }[/math] state is not interpreted as the non-existence of the photon, but is instead a photon in a "vacuum quantum state." This photon can interact with a detector and show up as [math]\displaystyle{ |0 \rangle }[/math] yet still carry information, allowing the bomb test to be interpreted in classical terms.^[13]

Experiments

In 1994, Anton Zeilinger, Paul Kwiat, Harald Weinfurter, and Thomas Herzog performed an equivalent of the above experiment, proving interaction-free measurements are indeed possible.^[14]

In 1996, Kwiat et al. devised a method, using a sequence of polarising devices, that efficiently increases the yield rate to a level arbitrarily close to one. The key idea is to split a fraction of the photon beam into a large number of beams of very small amplitude and reflect all of them off the mirror, recombining them with the original beam afterwards.^[14]^[15] It can also be argued that this revised construction is simply equivalent to a resonant cavity and the result looks much less shocking^{[to whom?]} in this language; see Watanabe and Inoue (2000).

In 2016, Carsten Robens, Wolfgang Alt, Clive Emary, Dieter Meschede, and Andrea Alberti^[16] demonstrated that the Elitzur–Vaidman bomb testing experiment can be recast in a rigorous test of the macro-realistic worldview based on the violation of the Leggett–Garg inequality using ideal negative measurements. In their experiment they perform the bomb test with a single atom trapped in a polarization-synthesized optical lattice. This optical lattice enables interaction-free measurements by entangling the spin and position of atoms.

References

Elitzur, Avshalom C.; Lev Vaidman (1993). "Quantum mechanical interaction-free measurements". Foundations of Physics 23 (7): 987–997. doi:10.1007/BF00736012. Bibcode: 1993FoPh...23..987E. http://www.tau.ac.il/~vaidman/lvhp/m28.pdf. Retrieved 2014-04-01.
P. G. Kwiat; H. Weinfurter; T. Herzog; A. Zeilinger; M. A. Kasevich (1995). "Interaction-free Measurement". Phys. Rev. Lett. 74 (24): 4763–4766. doi:10.1103/PhysRevLett.74.4763. PMID 10058593. Bibcode: 1995PhRvL..74.4763K.
Z. Blanco-Garcia and O. Rosas-Ortiz, Interaction-Free Measurements of Optical Semitransparent Objects, J. Phys.: Conf. Ser. 698:012013, 2016
A. Peruzzo, P. Shadbolt, N. Brunner, S. Popescu and J.L. O'Brien, A Quantum Delayed-Choice Experiment, Science 338:634–637, 2012
F. Kaiser, T. Coudreau, P. Milman, D.B. Ostroswsky and S. Tanzilli, Entanglement-Enabled Delayed-Choice Experiment Science 338:637–640, 2012
Vazirani, Umesh (2005-11-13). "Applications of Quantum Search, Quantum Zeno Effect". EECS Berkeley. https://inst.eecs.berkeley.edu/~cs191/fa07/lectures/lecture22_fa07.pdf.

Notes

↑ Paul G. Kwiat; H. Weinfurter; T. Herzog; A. Zeilinger; M. Kasevich (1994). "Experimental realization of "interaction-free" measurements". Fundamental Problems in Quantum Theory 755: 383–393. doi:10.1111/j.1749-6632.1995.tb38981.x. Bibcode: 1995NYASA.755..383K. http://www.univie.ac.at/qfp/publications3/pdffiles/1994-08.pdf. Retrieved 2012-05-07.
↑ ^2.0 ^2.1 Elitzur Vaidman 1993, p. 988.
↑ ^3.0 ^3.1 Elitzur Vaidman 1993, p. 991.
↑ Keith Bowden (1997-03-15). "Can Schrodinger's Cat Collapse the Wavefunction?". http://nonlocal.com/quantum-d/v2/kbowden_03-15-97.html.
↑ ^5.0 ^5.1 Elitzur Vaidman 1993, p. 992.
↑ Feynman, Richard P.; Robert B. Leighton; Matthew Sands (1965). The Feynman Lectures on Physics, Vol. 3. US: Addison-Wesley. pp. 1.5. ISBN 978-0201021189.
↑ ^7.0 ^7.1 Elitzur Vaidman 1993, p. 990.
↑ ^8.0 ^8.1 Elitzur Vaidman 1993, p. 994.
↑ Pinto, Vinícius Pereira; Pereira de Oliveira, Bruno; Mitsue Yasuoka, Fátima Maria; Courteille, Philippe Wilhelm; Caiado de Castro Neto, Jarbas (2023-09-24). "Exploring Quantum Comprehension Through the Elitzur-Vaidman Bomb Testing Problem" (in en). Brazilian Journal of Physics 53 (6): 152. doi:10.1007/s13538-023-01366-x. ISSN 1678-4448. https://doi.org/10.1007/s13538-023-01366-x.
↑ Vazirani 2005.
↑ Bricmont, Jean (2016), "The de Broglie–Bohm Theory" (in en), Making Sense of Quantum Mechanics (Springer International Publishing): pp. 129–197, doi:10.1007/978-3-319-25889-8_5, ISBN 978-3-319-25887-4, http://link.springer.com/10.1007/978-3-319-25889-8_5, retrieved 2021-02-23
↑ Leifer, Matthew Saul (2014-11-05). "Is the Quantum State Real? An Extended Review of ψ-ontology Theorems". Quanta 3 (1): 67. doi:10.12743/quanta.v3i1.22. ISSN 1314-7374. http://quanta.ws/ojs/index.php/quanta/article/view/22.
↑ Catani, Lorenzo; Leifer, Matthew; Schmid, David; Spekkens, Robert W. (2023-09-25). "Why interference phenomena do not capture the essence of quantum theory". Quantum 7: 1119. doi:10.22331/q-2023-09-25-1119. ISSN 2521-327X. Bibcode: 2023Quant...7.1119C. "Specifically, even if the occupation number of a mode is 0, there are two possible values that its discrete phase might take, and hence such a mode can still encode one bit of information. This is what opens up the possibility that information about a device (e.g., whether it implements a which-way measurement or not) can be propagated to other devices (such as the final detectors) through a mode which, in the quantum account, is in the vacuum quantum state. In particular, in the case of the Elitzur-Vaidman bomb-tester, it is what opens up the possibility that information about whether the bomb is functional or faulty can be propagated to the final detectors through the physical state of the R mode even though in the quantum account the R mode is in the vacuum quantum state.".
↑ ^14.0 ^14.1 Kwiat, et al. 1995, pp. 4763-4766.
↑ Hosten, Onur; Rakher, Matthew T.; Barreiro, Julio T.; Peters, Nicholas A.; Kwiat, Paul G. (February 23, 2006). "Counterfactual quantum computation through quantum interrogation". Nature 439 (7079): 949–952. doi:10.1038/nature04523. ISSN 0028-0836. PMID 16495993. Bibcode: 2006Natur.439..949H.
↑ Carsten Robens; Wolfgang Alt; Clive Emary; Dieter Meschede; Andrea Alberti (19 December 2016). "Atomic "bomb testing": the Elitzur–Vaidman experiment violates the Leggett–Garg inequality". Applied Physics B 123 (1): 12. doi:10.1007/s00340-016-6581-y. PMID 32214686. Bibcode: 2017ApPhB.123...12R.

v t e Quantum mechanics
Background	Introduction History timeline Glossary Classical mechanics Old quantum theory
Fundamentals	Bra–ket notation Casimir effect Complementarity Density matrix Energy level ground state excited state degenerate levels Vacuum state Zero-point energy QED vacuum QCD vacuum Hamiltonian Operator Quantum coherence Quantum decoherence Measurement Quantum Quantum realm Quantum system Quantum state Quantum number Quantum entanglement Quantum superposition Quantum nonlocality Quantum tunnelling Quantum levitation Quantum fluctuation Quantum annealing Quantum foam Quantum noise Heisenberg uncertainty principle Spontaneous parametric down-conversion Von Neumann entropy Spin Scattering theory Symmetry in quantum mechanics Symmetry breaking Spontaneous symmetry breaking Wave propagation Quantum interference Wave function Wave function collapse Wave–particle duality Matter wave Qubit Qutrit Observable Probability distribution
Formulations	Formulations Heisenberg Interaction Matrix mechanics Schrödinger Path integral formulation Phase space
Equations	Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations	Interpretations Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden variables Many worlds Objective collapse Quantum logic Relational Stochastic Transactional Cosmological
Experiments	Afshar Bell's inequality Cold Atom Laboratory Davisson–Germer Delayed-choice quantum eraser Double-slit Franck–Hertz experiment Leggett–Garg inequality Mach-Zehnder inter. Elitzur–Vaidman Popper Quantum eraser Schrödinger's cat Quantum suicide and immortality Stern–Gerlach Wheeler's delayed choice
Science	Q-analog List Quantum algebra Quantum calculus Quantum differential calculus Quantum geometry Quantum group Quantum Bayesianism Quantum biology Quantum chemistry Quantum chaos Quantum cognition Quantum cosmology Quantum dynamics Quantum economics Quantum evolution Quantum finance Quantum game theory Quantum measurement problem Quantum mind Quantum probability Quantum social science Quantum stochastic calculus Quantum spacetime
Technology	Quantum algorithms Quantum amplifier Quantum cellular automata Quantum finite automata Quantum electronics Quantum logic gates Quantum clock Quantum channel Quantum bus Quantum circuit Phase qubit Matrix isolation Quantum dot Quantum dot display Quantum dot solar cell Quantum dot cellular automaton Quantum dot single-photon source Quantum dot laser Quantum well Quantum computing Timeline Quantum cryptography Post-quantum cryptography Quantum error correction Quantum imaging Quantum image processing Quantum information Quantum key distribution Quantum machine Quantum machine learning Quantum metamaterial Quantum metrology Quantum network Quantum neural network Quantum optics Quantum programming Quantum sensors Quantum simulator Quantum teleportation Quantum levitation Time travel Quantum complexity theory
Extensions	Quantum statistical mechanics Relativistic quantum mechanics Quantum field theory Axiomatic quantum field theory Quantum field theory in curved spacetime Thermal quantum field theory Topological quantum field theory Local quantum field theory Conformal field theory Two-dimensional conformal field theory Liouville field theory History Quantum gravity
Category Physics Portal Physics WikiProject Commons

Anonymous

Search

Elitzur–Vaidman bomb tester

Namespaces

More

Page actions

Contents

Background