Physics:Stationary-action principle

From HandWiki
Short description: Variational principle in physics
Part of a series on
Classical mechanics
[math]\displaystyle{ \textbf{F} = \frac{d}{dt} (m\textbf{v}) }[/math]
Second law of motion
Branches
Fundamentals
Formulations
Core topics
Rotation
Categories
Classical mechanics

The stationary-action principle – also known as the principle of least action – is a variational principle that, when applied to the action of a mechanical system, yields the equations of motion for that system. The principle states that the trajectories (i.e. the solutions of the equations of motion) are stationary points of the system's action functional.[1]

The term "least action" is often used[1] by physicists even though the principle has no general minimality requirement.[2] Historically the principle was known as "least action" and Feynman adopted this name over "Hamilton's principle" when he adapted it for quantum mechanics.[3]

The principle can be used to derive Newtonian, Lagrangian and Hamiltonian equations of motion, and even general relativity, as well as classical electrodynamics and quantum field theory. In these cases, a different action must be minimized or maximized. For relativity, it is the Einstein–Hilbert action. For quantum field theory, it involves the path integral formulation.

The classical mechanics and electromagnetic expressions are a consequence of quantum mechanics. The stationary action method helped in the development of quantum mechanics.[4]

The principle remains central in modern physics and mathematics, being applied in thermodynamics,[5][6][7] fluid mechanics,[8] the theory of relativity, quantum mechanics,[9] particle physics, and string theory[10] and is a focus of modern mathematical investigation in Morse theory. Maupertuis' principle and Hamilton's principle exemplify the principle of stationary action.

Scholars often credit Pierre Louis Maupertuis for formulating the principle of least action because he wrote about it in 1744[11] and 1746.[12]

General statement

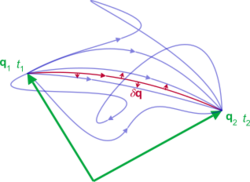
As the system evolves, q traces a path through configuration space (only some are shown). The path taken by the system (red) has a stationary action (δS = 0) under small changes in the configuration of the system (δq).[13]

The action, denoted [math]\displaystyle{ \mathcal{S} }[/math], of a physical system is defined as the integral of the Lagrangian L between two instants of time t1 and t2 – technically a functional of the N generalized coordinates q = (q1, q2, ... , qN) which are functions of time and define the configuration of the system:

[math]\displaystyle{ \mathbf{q} : \mathbf{R} \to \mathbf{R}^N }[/math] [math]\displaystyle{ \mathcal{S}[\mathbf{q}, t_1, t_2] = \int_{t_1}^{t_2} L(\mathbf{q}(t),\mathbf{\dot{q}}(t), t) dt }[/math] where the dot denotes the time derivative, and t is time.

Mathematically the principle is[14][15] [math]\displaystyle{ \delta \mathcal{S} = 0 , }[/math] where δ (lowercase Greek delta) means a small change. In words this reads:[13]

The path taken by the system between times t1 and t2 and configurations q1 and q2 is the one for which the action is stationary (no change) to first order.

Stationary action is not always a minimum, despite the historical name of least action.[16][1]:19-6 It is a minimum principle for sufficiently short, finite segments in the path of a finite-dimensional system.[2]

In applications the statement and definition of action are taken together in "Hamilton's principle", written in modern form as:[17] [math]\displaystyle{ \delta \int_{t_1}^{t_2} L(\mathbf{q}, \mathbf{\dot{q}},t) dt = 0 . }[/math]

The action and Lagrangian both contain the dynamics of the system for all times. The term "path" simply refers to a curve traced out by the system in terms of the coordinates in the configuration space, i.e. the curve q(t), parameterized by time (see also parametric equation for this concept).

History

Main page: Physics:History of variational principles in physics

The action principle is preceded by earlier ideas in optics. In Ancient Greece , Euclid wrote in his Catoptrica that, for the path of light reflecting from a mirror, the angle of incidence equals the angle of reflection.[18] Hero of Alexandria later showed that this path was the shortest length and least time.[19]

Building on the early work of Pierre Louis Maupertuis, Leonhard Euler, and Joseph Louis Lagrange defining versions of principle of least action,[20]:580 William Rowan Hamilton and in tandem Carl Gustav Jacobi developed a variational form for classical mechanics known as the Hamilton–Jacobi equation.[21]:201

In 1915 David Hilbert applied the variational principle to derive Albert Einstein's equations of general relativity.[22]

In 1933, the physicist Paul Dirac demonstrated how this principle can be used in quantum calculations by discerning the quantum mechanical underpinning of the principle in the quantum interference of amplitudes.[23] Subsequently Julian Schwinger and Richard Feynman independently applied this principle in quantum electrodynamics.[24][25]

Disputes about possible teleological aspects

The mathematical equivalence of the differential equations of motion and their integral counterpart has important philosophical implications. The differential equations are statements about quantities localized to a single point in space or single moment of time. For example, Newton's second law [math]\displaystyle{ \mathbf{F} = m\mathbf{a} }[/math] states that the instantaneous force F applied to a mass m produces an acceleration a at the same instant. By contrast, the action principle is not localized to a point; rather, it involves integrals over an interval of time and (for fields) an extended region of space. Moreover, in the usual formulation of classical action principles, the initial and final states of the system are fixed, e.g.,

Given that the particle begins at position x1 at time t1 and ends at position x2 at time t2, the physical trajectory that connects these two endpoints is an extremum of the action integral.

In particular, the fixing of the final state has been interpreted as giving the action principle a teleological character which has been controversial historically. However, according to Wolfgang Yourgrau (de) and Stanley Mandelstam, the teleological approach... presupposes that the variational principles themselves have mathematical characteristics which they de facto do not possess[26] In addition, some critics maintain this apparent teleology occurs because of the way in which the question was asked. By specifying some but not all aspects of both the initial and final conditions (the positions but not the velocities) we are making some inferences about the initial conditions from the final conditions, and it is this "backward" inference that can be seen as a teleological explanation.

See also


Notes and references

  1. ↑ 1.0 1.1 1.2 The Feynman Lectures on Physics Vol. II Ch. 19: The Principle of Least Action
  2. ↑ 2.0 2.1 Stehle, Philip M. (1993). "Least-action principle". in Parker, S. P.. McGraw-Hill Encyclopaedia of Physics (2nd ed.). New York: McGraw-Hill. p. 670. ISBN 0-07-051400-3. https://archive.org/details/mcgrawhillencycl1993park/page/670/mode/2up. 
  3. ↑ Moore, Thomas A. (2004-04-01). "Getting the most action out of least action: A proposal" (in en). American Journal of Physics 72 (4): 522–527. doi:10.1119/1.1646133. ISSN 0002-9505. Bibcode: 2004AmJPh..72..522M. https://pubs.aip.org/ajp/article/72/4/522/1056045/Getting-the-most-action-out-of-least-action-A. 
  4. ↑ Richard Feynman, The Character of Physical Law.
  5. ↑ García-Morales, Vladimir; Pellicer, Julio; Manzanares, José A. (2008). "Thermodynamics based on the principle of least abbreviated action: Entropy production in a network of coupled oscillators". Annals of Physics 323 (8): 1844–58. doi:10.1016/j.aop.2008.04.007. Bibcode: 2008AnPhy.323.1844G. 
  6. ↑ Gay-Balmaz, François; Yoshimura, Hiroaki (2018). "From Lagrangian Mechanics to Nonequilibrium Thermodynamics: A Variational Perspective" (in en). Entropy 21 (1): 8. doi:10.3390/e21010008. ISSN 1099-4300. PMID 33266724. Bibcode: 2018Entrp..21....8G. 
  7. ↑ Biot, Maurice Anthony (1975). "A virtual dissipation principle and Lagrangian equations in non-linear irreversible thermodynamics". Bulletin de la Classe des sciences 61 (1): 6–30. doi:10.3406/barb.1975.57878. ISSN 0001-4141. 
  8. ↑ Gray, Chris (2009). "Principle of least action". Scholarpedia 4 (12): 8291. doi:10.4249/scholarpedia.8291. Bibcode: 2009SchpJ...4.8291G. 
  9. ↑ Feynman, Richard Phillips (1942), The Principle of Least Action in Quantum Mechanics, Bibcode: 1942PhDT.........5F 
  10. ↑ "Principle of Least Action – damtp". http://www.damtp.cam.ac.uk/user/db275/LeastAction.pdf. 
  11. ↑ P.L.M. de Maupertuis, Accord de différentes lois de la nature qui avaient jusqu'ici paru incompatibles. (1744) Mém. As. Sc. Paris p. 417. (English translation)
  12. ↑ P.L.M. de Maupertuis, Le lois de mouvement et du repos, déduites d'un principe de métaphysique. (1746) Mém. Ac. Berlin, p. 267.(English translation)
  13. ↑ 13.0 13.1 R. Penrose (2007). The Road to Reality. Vintage books. p. 474. ISBN 978-0-679-77631-4. 
  14. ↑ Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
  15. ↑ Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN:978-0-521-57572-0
  16. ↑ Goodman, Bernard (1993). "Action". in Parker, S. P.. McGraw-Hill Encyclopaedia of Physics (2nd ed.). New York: McGraw-Hill. p. 22. ISBN 0-07-051400-3. https://archive.org/details/mcgrawhillencycl1993park/page/22/mode/2up. 
  17. ↑ Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN:0-07-084018-0
  18. ↑ "Optics from Euclid to Huygens". Applied Optics 5 (9): 1383–93. 1966. doi:10.1364/AO.5.001383. PMID 20057555. Bibcode: 1966ApOpt...5.1383H. "In Catoptrics the law of reflection is stated, namely that incoming and outgoing rays form the same angle with the surface normal.". 
  19. ↑ Kline, Morris (1972). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. pp. 167–68. ISBN 0-19-501496-0. https://archive.org/details/mathematicalthou0000unse. 
  20. ↑ Kline, Morris (1972). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. pp. 167–168. ISBN 0-19-501496-0. https://archive.org/details/mathematicalthou0000unse. 
  21. ↑ Nakane, Michiyo, and Craig G. Fraser. "The Early History of Hamilton‐Jacobi Dynamics 1834–1837." Centaurus 44.3‐4 (2002): 161-227.
  22. ↑ Mehra, Jagdish (1987). "Einstein, Hilbert, and the Theory of Gravitation". in Mehra, Jagdish. The physicist's conception of nature (Reprint ed.). Dordrecht: Reidel. ISBN 978-90-277-2536-3. 
  23. ↑ Dirac, Paul A. M. (1933). "The Lagrangian in Quantum Mechanics". Physikalische Zeitschrift der Sowjetunion 3 (1): 64–72. http://www.hep.anl.gov/czachos/soysoy/Dirac33.pdf. 
  24. ↑ R. Feynman, Quantum Mechanics and Path Integrals, McGraw-Hill (1965), ISBN:0-07-020650-3
  25. ↑ J. S. Schwinger, Quantum Kinematics and Dynamics, W. A. Benjamin (1970), ISBN:0-7382-0303-3
  26. ↑ Stöltzner, Michael (1994). "Action Principles and Teleology". Inside Versus Outside. Springer Series in Synergetics. 63. Berlin: Springer. pp. 33–62. doi:10.1007/978-3-642-48647-0_3. ISBN 978-3-642-48649-4. 

Further reading

For an annotated bibliography, see Edwin F. Taylor who lists, among other things, the following books

  • Cornelius Lanczos, The Variational Principles of Mechanics (Dover Publications, New York, 1986). ISBN:0-486-65067-7. The reference most quoted by all those who explore this field.
  • L. D. Landau and E. M. Lifshitz, Mechanics, Course of Theoretical Physics (Butterworth-Heinenann, 1976), 3rd ed., Vol. 1. ISBN:0-7506-2896-0. Begins with the principle of least action.
  • Thomas A. Moore "Least-Action Principle" in Macmillan Encyclopedia of Physics (Simon & Schuster Macmillan, 1996), Volume 2, ISBN:0-02-897359-3, OCLC 35269891, pages 840–842.
  • Gerald Jay Sussman and Jack Wisdom, Structure and Interpretation of Classical Mechanics (MIT Press, 2001). Begins with the principle of least action, uses modern mathematical notation, and checks the clarity and consistency of procedures by programming them in computer language.
  • Dare A. Wells, Lagrangian Dynamics, Schaum's Outline Series (McGraw-Hill, 1967) ISBN:0-07-069258-0, A 350-page comprehensive "outline" of the subject.
  • Robert Weinstock, Calculus of Variations, with Applications to Physics and Engineering (Dover Publications, 1974). ISBN:0-486-63069-2. An oldie but goodie, with the formalism carefully defined before use in physics and engineering.
  • Wolfgang Yourgrau and Stanley Mandelstam, Variational Principles in Dynamics and Quantum Theory (Dover Publications, 1979). A nice treatment that does not avoid the philosophical implications of the theory and lauds the Feynman treatment of quantum mechanics that reduces to the principle of least action in the limit of large mass.

External links

de:Prinzip der kleinsten Wirkung sq:Principi i Hamiltonit



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Stationary-action_principle&oldid=3282880"