Scalar multiplication

Short description: Algebraic operation

Scalar multiplication of a vector by a factor of 3 stretches the vector out.

The scalar multiplications −a and 2a of a vector a

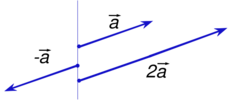
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra (or more generally, a module in abstract algebra). In common geometrical contexts, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction. Scalar multiplication is the multiplication of a vector by a scalar (where the product is a vector), and is to be distinguished from inner product of two vectors (where the product is a scalar).

Definition

In general, if K is a field and V is a vector space over K, then scalar multiplication is a function from K × V to V. The result of applying this function to k in K and v in V is denoted kv.

Properties

Scalar multiplication obeys the following rules (vector in boldface):

• Additivity in the scalar: (c + d)v = cv + dv;
• Additivity in the vector: c(v + w) = cv + cw;
• Compatibility of product of scalars with scalar multiplication: (cd)v = c(dv);
• Multiplying by 1 does not change a vector: 1v = v;
• Multiplying by 0 gives the zero vector: 0v = 0;
• Multiplying by −1 gives the additive inverse: (−1)v = −v.

Here, + is addition either in the field or in the vector space, as appropriate; and 0 is the additive identity in either. Juxtaposition indicates either scalar multiplication or the multiplication operation in the field.

Interpretation

The space of vectors may be considered a coordinate space where elements are associated with a list of elements from K. The units of the field form a group K ^× and the scalar-vector multiplication is a group action on the coordinate space by K ^×. The zero of the field acts on the coordinate space to collapse it to the zero vector.

When K is the field of real numbers there is a geometric interpretation of scalar multiplication: it stretches or contracts vectors by a constant factor. As a result, it produces a vector in the same or opposite direction of the original vector but of a different length.

As a special case, V may be taken to be K itself and scalar multiplication may then be taken to be simply the multiplication in the field.

When V is Kⁿ, scalar multiplication is equivalent to multiplication of each component with the scalar, and may be defined as such.

The same idea applies if K is a commutative ring and V is a module over K. K can even be a rig, but then there is no additive inverse. If K is not commutative, the distinct operations left scalar multiplication cv and right scalar multiplication vc may be defined.

Scalar multiplication of matrices

The left scalar multiplication of a matrix A with a scalar λ gives another matrix of the same size as A. It is denoted by λA, whose entries of λA are defined by

[math]\displaystyle{ (\lambda \mathbf{A})_{ij} = \lambda\left(\mathbf{A}\right)_{ij}\,, }[/math]

explicitly:

[math]\displaystyle{ \lambda \mathbf{A} = \lambda \begin{pmatrix} A_{11} & A_{12} & \cdots & A_{1m} \\ A_{21} & A_{22} & \cdots & A_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ A_{n1} & A_{n2} & \cdots & A_{nm} \\ \end{pmatrix} = \begin{pmatrix} \lambda A_{11} & \lambda A_{12} & \cdots & \lambda A_{1m} \\ \lambda A_{21} & \lambda A_{22} & \cdots & \lambda A_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ \lambda A_{n1} & \lambda A_{n2} & \cdots & \lambda A_{nm} \\ \end{pmatrix}\,. }[/math]

Similarly, even though there is no widely-accepted definition, the right scalar multiplication of a matrix A with a scalar λ could be defined to be

[math]\displaystyle{ (\mathbf{A}\lambda)_{ij} = \left(\mathbf{A}\right)_{ij} \lambda\,, }[/math]

explicitly:

[math]\displaystyle{ \mathbf{A}\lambda = \begin{pmatrix} A_{11} & A_{12} & \cdots & A_{1m} \\ A_{21} & A_{22} & \cdots & A_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ A_{n1} & A_{n2} & \cdots & A_{nm} \\ \end{pmatrix}\lambda = \begin{pmatrix} A_{11} \lambda & A_{12} \lambda & \cdots & A_{1m} \lambda \\ A_{21} \lambda & A_{22} \lambda & \cdots & A_{2m} \lambda \\ \vdots & \vdots & \ddots & \vdots \\ A_{n1} \lambda & A_{n2} \lambda & \cdots & A_{nm} \lambda \\ \end{pmatrix}\,. }[/math]

When the entries of the matrix and the scalars are from the same commutative field, for example, the real number field or the complex number field, these two multiplications are the same, and can be simply called scalar multiplication. For matrices over a more general field that is not commutative, they may not be equal.

For a real scalar and matrix:

[math]\displaystyle{ \lambda = 2, \quad \mathbf{A} =\begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} }[/math]

[math]\displaystyle{ 2 \mathbf{A} = 2 \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} = \begin{pmatrix} 2 \!\cdot\! a & 2 \!\cdot\! b \\ 2 \!\cdot\! c & 2 \!\cdot\! d \\ \end{pmatrix} = \begin{pmatrix} a \!\cdot\! 2 & b \!\cdot\! 2 \\ c \!\cdot\! 2 & d \!\cdot\! 2 \\ \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix}2= \mathbf{A}2. }[/math]

For quaternion scalars and matrices:

[math]\displaystyle{ \lambda = i, \quad \mathbf{A} = \begin{pmatrix} i & 0 \\ 0 & j \\ \end{pmatrix} }[/math]

[math]\displaystyle{ i\begin{pmatrix} i & 0 \\ 0 & j \\ \end{pmatrix} = \begin{pmatrix} i^2 & 0 \\ 0 & ij \\ \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & k \\ \end{pmatrix} \ne \begin{pmatrix} -1 & 0 \\ 0 & -k \\ \end{pmatrix} = \begin{pmatrix} i^2 & 0 \\ 0 & ji \\ \end{pmatrix} = \begin{pmatrix} i & 0 \\ 0 & j \\ \end{pmatrix}i\,, }[/math]

where i, j, k are the quaternion units. The non-commutativity of quaternion multiplication prevents the transition of changing ij = +k to ji = −k.

See also

• Dot product
• Matrix multiplication
• Multiplication of vectors
• Product (mathematics)