Physics:Simple harmonic motion
| Part of a series on |
| Classical mechanics |
|---|
| [math]\displaystyle{ \textbf{F} = \frac{d}{dt} (m\textbf{v}) }[/math] |
In mechanics and physics, simple harmonic motion (sometimes abbreviated SHM) is a special type of periodic motion an object experiences due to a restoring force whose magnitude is directly proportional to the distance of the object from an equilibrium position and acts towards the equilibrium position. It results in an oscillation that is described by a sinusoid which continues indefinitely (if uninhibited by friction or any other dissipation of energy).
Simple harmonic motion can serve as a mathematical model for a variety of motions, but is typified by the oscillation of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's law. The motion is sinusoidal in time and demonstrates a single resonant frequency. Other phenomena can be modeled by simple harmonic motion, including the motion of a simple pendulum, although for it to be an accurate model, the net force on the object at the end of the pendulum must be proportional to the displacement (and even so, it is only a good approximation when the angle of the swing is small; see small-angle approximation). Simple harmonic motion can also be used to model molecular vibration.
Simple harmonic motion provides a basis for the characterization of more complicated periodic motion through the techniques of Fourier analysis.
Introduction
The motion of a particle moving along a straight line with an acceleration whose direction is always towards a fixed point on the line and whose magnitude is proportional to the displacement from the fixed point is called simple harmonic motion.[1]
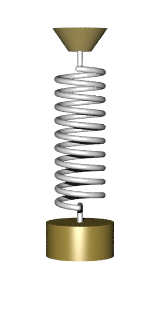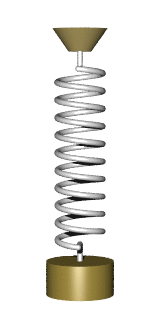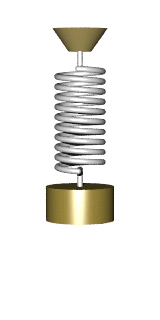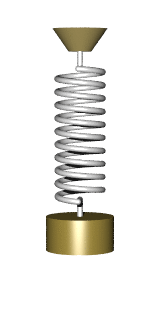
In the diagram, a simple harmonic oscillator, consisting of a weight attached to one end of a spring, is shown. The other end of the spring is connected to a rigid support such as a wall. If the system is left at rest at the equilibrium position then there is no net force acting on the mass. However, if the mass is displaced from the equilibrium position, the spring exerts a restoring elastic force that obeys Hooke's law.
Mathematically, the restoring force F is given by [math]\displaystyle{ \mathbf{F}=-k\mathbf{x}, }[/math] where F is the restoring elastic force exerted by the spring (in SI units: N), k is the spring constant (N·m−1), and x is the displacement from the equilibrium position (m).
For any simple mechanical harmonic oscillator:
- When the system is displaced from its equilibrium position, a restoring force that obeys Hooke's law tends to restore the system to equilibrium.
Once the mass is displaced from its equilibrium position, it experiences a net restoring force. As a result, it accelerates and starts going back to the equilibrium position. When the mass moves closer to the equilibrium position, the restoring force decreases. At the equilibrium position, the net restoring force vanishes. However, at x = 0, the mass has momentum because of the acceleration that the restoring force has imparted. Therefore, the mass continues past the equilibrium position, compressing the spring. A net restoring force then slows it down until its velocity reaches zero, whereupon it is accelerated back to the equilibrium position again.
As long as the system has no energy loss, the mass continues to oscillate. Thus simple harmonic motion is a type of periodic motion. If energy is lost in the system, then the mass exhibits damped oscillation.
Note if the real space and phase space plot are not co-linear, the phase space motion becomes elliptical. The area enclosed depends on the amplitude and the maximum momentum.
Dynamics
In Newtonian mechanics, for one-dimensional simple harmonic motion, the equation of motion, which is a second-order linear ordinary differential equation with constant coefficients, can be obtained by means of Newton's 2nd law and Hooke's law for a mass on a spring.
[math]\displaystyle{ F_\mathrm{net} = m\frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -kx, }[/math] where m is the inertial mass of the oscillating body, x is its displacement from the equilibrium (or mean) position, and k is a constant (the spring constant for a mass on a spring).
Therefore, [math]\displaystyle{ \frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -\frac{k}{m}x, }[/math]
Solving the differential equation above produces a solution that is a sinusoidal function: [math]\displaystyle{ x(t) = c_1\cos\left(\omega t\right) + c_2\sin\left(\omega t\right), }[/math] where [math]\displaystyle{ \omega = \sqrt{{k}/{m}}. }[/math] The meaning of the constants [math]\displaystyle{ c_1 }[/math] and [math]\displaystyle{ c_2 }[/math] can be easily found: setting [math]\displaystyle{ t=0 }[/math] on the equation above we see that [math]\displaystyle{ x(0) = c_1 }[/math], so that [math]\displaystyle{ c_1 }[/math] is the initial position of the particle, [math]\displaystyle{ c_1=x_0 }[/math]; taking the derivative of that equation and evaluating at zero we get that [math]\displaystyle{ \dot{x}(0) = \omega c_2 }[/math], so that [math]\displaystyle{ c_2 }[/math] is the initial speed of the particle divided by the angular frequency, [math]\displaystyle{ c_2 = \frac{v_0}{\omega} }[/math]. Thus we can write: [math]\displaystyle{ x(t) = x_0 \cos\left(\sqrt{\frac{k}{m}} t\right) + \frac{v_0}{\sqrt{\frac{k}{m}}}\sin\left(\sqrt{\frac{k}{m}} t\right). }[/math]
This equation can also be written in the form: [math]\displaystyle{ x(t) = A\cos\left(\omega t - \varphi\right), }[/math] where
- [math]\displaystyle{ A = \sqrt{{c_1}^2 + {c_2}^2} }[/math]
- [math]\displaystyle{ \tan \varphi = \frac{c_2}{c_1}, }[/math]
- [math]\displaystyle{ \sin \varphi = \frac{c_2}{A}, \; \cos \varphi = \frac{c_1}{A} }[/math]
or equivalently
- [math]\displaystyle{ A = |c_1 + c_2i|, }[/math]
- [math]\displaystyle{ \varphi = \arg(c_1 + c_2i) }[/math]
In the solution, c1 and c2 are two constants determined by the initial conditions (specifically, the initial position at time t = 0 is c1, while the initial velocity is c2ω), and the origin is set to be the equilibrium position.[A] Each of these constants carries a physical meaning of the motion: A is the amplitude (maximum displacement from the equilibrium position), ω = 2πf is the angular frequency, and φ is the initial phase.[B]
Using the techniques of calculus, the velocity and acceleration as a function of time can be found: [math]\displaystyle{ v(t) = \frac{\mathrm{d} x}{\mathrm{d} t} = - A\omega \sin(\omega t-\varphi), }[/math]
- Speed: [math]\displaystyle{ {\omega} \sqrt {A^2 - x^2} }[/math]
- Maximum speed: v = ωA (at equilibrium point)
[math]\displaystyle{ a(t) = \frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = - A \omega^2 \cos( \omega t-\varphi). }[/math]
- Maximum acceleration: Aω2 (at extreme points)
By definition, if a mass m is under SHM its acceleration is directly proportional to displacement. [math]\displaystyle{ a(x) = -\omega^2 x. }[/math] where [math]\displaystyle{ \omega^2=\frac{k}{m} }[/math]
Since ω = 2πf, [math]\displaystyle{ f = \frac{1}{2\pi}\sqrt{\frac{k}{m}}, }[/math] and, since T = 1/f where T is the time period, [math]\displaystyle{ T = 2\pi \sqrt{\frac{m}{k}}. }[/math]
These equations demonstrate that the simple harmonic motion is isochronous (the period and frequency are independent of the amplitude and the initial phase of the motion).
Energy
Substituting ω2 with k/m, the kinetic energy K of the system at time t is [math]\displaystyle{ K(t) = \tfrac12 mv^2(t) = \tfrac12 m\omega^2A^2\sin^2(\omega t - \varphi) = \tfrac12 kA^2 \sin^2(\omega t - \varphi), }[/math] and the potential energy is [math]\displaystyle{ U(t) = \tfrac12 k x^2(t) = \tfrac12 k A^2 \cos^2(\omega t - \varphi). }[/math] In the absence of friction and other energy loss, the total mechanical energy has a constant value [math]\displaystyle{ E = K + U = \tfrac12 k A^2. }[/math]
Examples
The following physical systems are some examples of simple harmonic oscillator.
Mass on a spring
A mass m attached to a spring of spring constant k exhibits simple harmonic motion in closed space. The equation for describing the period [math]\displaystyle{ T= 2 \pi\sqrt\frac{m}{k} }[/math] shows the period of oscillation is independent of the amplitude, though in practice the amplitude should be small. The above equation is also valid in the case when an additional constant force is being applied on the mass, i.e. the additional constant force cannot change the period of oscillation.
Uniform circular motion
Simple harmonic motion can be considered the one-dimensional projection of uniform circular motion. If an object moves with angular speed ω around a circle of radius r centered at the origin of the xy-plane, then its motion along each coordinate is simple harmonic motion with amplitude r and angular frequency ω.
Oscillatory motion
It is the motion of a body when it moves to and fro about a definite point. This type of motion is also called oscillatory motion or vibratory motion. The time period is able to be calculated by [math]\displaystyle{ T= 2 \pi\sqrt\frac{l}{g} }[/math] where l is the distance from rotation to centre of mass of object undergoing SHM and g being gravitational field constant. This is analogous to the mass-spring system.
Mass of a simple pendulum
 |
In the small-angle approximation, the motion of a simple pendulum is approximated by simple harmonic motion. The period of a mass attached to a pendulum of length l with gravitational acceleration [math]\displaystyle{ g }[/math] is given by [math]\displaystyle{ T = 2 \pi \sqrt\frac{l}{g} }[/math]
This shows that the period of oscillation is independent of the amplitude and mass of the pendulum but not of the acceleration due to gravity, [math]\displaystyle{ g }[/math], therefore a pendulum of the same length on the Moon would swing more slowly due to the Moon's lower gravitational field strength. Because the value of [math]\displaystyle{ g }[/math] varies slightly over the surface of the earth, the time period will vary slightly from place to place and will also vary with height above sea level.
This approximation is accurate only for small angles because of the expression for angular acceleration α being proportional to the sine of the displacement angle: [math]\displaystyle{ -m g l \sin\theta=I \alpha, }[/math] where I is the moment of inertia. When θ is small, sin θ ≈ θ and therefore the expression becomes [math]\displaystyle{ -m g l \theta=I \alpha }[/math] which makes angular acceleration directly proportional and opposite to θ, satisfying the definition of simple harmonic motion (that net force is directly proportional to the displacement from the mean position and is directed towards the mean position).
Scotch yoke
A Scotch yoke mechanism can be used to convert between rotational motion and linear reciprocating motion. The linear motion can take various forms depending on the shape of the slot, but the basic yoke with a constant rotation speed produces a linear motion that is simple harmonic in form.
See also
Notes
- ^ The choice of using a cosine in this equation is a convention. Other valid formulations are: [math]\displaystyle{ x(t) = A\sin\left(\omega t +\varphi'\right), }[/math] where [math]\displaystyle{ \tan \varphi' = \frac{c_1}{c_2}, }[/math] since cos θ = sin(π/2 − θ).
- ^ The maximum displacement (that is, the amplitude), xmax, occurs when cos(ωt ± φ) = 1, and thus when xmax = A.
References
- Fowles, Grant R.; Cassiday, George L. (2005). Analytical Mechanics (7th ed.). Thomson Brooks/Cole. ISBN 0-534-49492-7.
- Taylor, John R. (2005). Classical Mechanics. University Science Books. ISBN 1-891389-22-X.
- Thornton, Stephen T.; Marion, Jerry B. (2003). Classical Dynamics of Particles and Systems (5th ed.). Brooks Cole. ISBN 0-534-40896-6.
- Walker, Jearl (2011). Principles of Physics (9th ed.). Hoboken, New Jersey: Wiley. ISBN 978-0-470-56158-4.
External links
- Simple Harmonic Motion from HyperPhysics
- Java simulation of spring-mass oscillator
- Geogebra applet for spring-mass, with 3 attached PDFs on SHM, driven/damped oscillators, spring-mass with friction
 |