Butterfly effect

File:Double pendulum simultaneous realisations.ogv
In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state.
The term is closely associated with the work of mathematician and meteorologist Edward Norton Lorenz. He noted that the butterfly effect is derived from the metaphorical example of the details of a tornado (the exact time of formation, the exact path taken) being influenced by minor perturbations such as a distant butterfly flapping its wings several weeks earlier. Lorenz originally used a seagull causing a storm but was persuaded to make it more poetic with the use of a butterfly and tornado by 1972.[1][2] He discovered the effect when he observed runs of his weather model with initial condition data that were rounded in a seemingly inconsequential manner. He noted that the weather model would fail to reproduce the results of runs with the unrounded initial condition data. A very small change in initial conditions had created a significantly different outcome.[3]
The idea that small causes may have large effects in weather was earlier acknowledged by French mathematician and physicist Henri Poincaré. American mathematician and philosopher Norbert Wiener also contributed to this theory. Lorenz's work placed the concept of instability of the Earth's atmosphere onto a quantitative base and linked the concept of instability to the properties of large classes of dynamic systems which are undergoing nonlinear dynamics and deterministic chaos.[4]
The butterfly effect concept has since been used outside the context of weather science as a broad term for any situation where a small change is supposed to be the cause of larger consequences.
History
In The Vocation of Man (1800), Johann Gottlieb Fichte says "you could not remove a single grain of sand from its place without thereby ... changing something throughout all parts of the immeasurable whole".
Chaos theory and the sensitive dependence on initial conditions were described in numerous forms of literature. This is evidenced by the case of the three-body problem by Poincaré in 1890.[5] He later proposed that such phenomena could be common, for example, in meteorology.[6]
In 1898, Jacques Hadamard noted general divergence of trajectories in spaces of negative curvature. Pierre Duhem discussed the possible general significance of this in 1908.[5]
In 1950, Alan Turing noted: "The displacement of a single electron by a billionth of a centimetre at one moment might make the difference between a man being killed by an avalanche a year later, or escaping."[7]
The idea that the death of one butterfly could eventually have a far-reaching ripple effect on subsequent historical events made its earliest known appearance in "A Sound of Thunder", a 1952 short story by Ray Bradbury. "A Sound of Thunder" features time travel.[8]
More precisely, though, almost the exact idea and the exact phrasing —of a tiny insect's wing affecting the entire atmosphere's winds— was published in a children's book which became extremely successful and well-known globally in 1962, the year before Lorenz published:
"...whatever we do affects everything and everyone else, if even in the tiniest way. Why, when a housefly flaps his wings, a breeze goes round the world."
-- The Princess of Pure Reason
In 1961, Lorenz was running a numerical computer model to redo a weather prediction from the middle of the previous run as a shortcut. He entered the initial condition 0.506 from the printout instead of entering the full precision 0.506127 value. The result was a completely different weather scenario.[9]
Lorenz wrote:
At one point I decided to repeat some of the computations in order to examine what was happening in greater detail. I stopped the computer, typed in a line of numbers that it had printed out a while earlier, and set it running again. I went down the hall for a cup of coffee and returned after about an hour, during which time the computer had simulated about two months of weather. The numbers being printed were nothing like the old ones. I immediately suspected a weak vacuum tube or some other computer trouble, which was not uncommon, but before calling for service I decided to see just where the mistake had occurred, knowing that this could speed up the servicing process. Instead of a sudden break, I found that the new values at first repeated the old ones, but soon afterward differed by one and then several units in the last [decimal] place, and then began to differ in the next to the last place and then in the place before that. In fact, the differences more or less steadily doubled in size every four days or so, until all resemblance with the original output disappeared somewhere in the second month. This was enough to tell me what had happened: the numbers that I had typed in were not the exact original numbers, but were the rounded-off values that had appeared in the original printout. The initial round-off errors were the culprits; they were steadily amplifying until they dominated the solution.
In 1963, Lorenz published a theoretical study of this effect in a highly cited, seminal paper called Deterministic Nonperiodic Flow[3][10] (the calculations were performed on a Royal McBee LGP-30 computer).[11][12] Elsewhere he stated:
One meteorologist remarked that if the theory were correct, one flap of a sea gull's wings would be enough to alter the course of the weather forever. The controversy has not yet been settled, but the most recent evidence seems to favor the sea gulls.[12]
Following proposals from colleagues, in later speeches and papers, Lorenz used the more poetic butterfly. According to Lorenz, when he failed to provide a title for a talk he was to present at the 139th meeting of the American Association for the Advancement of Science in 1972, Philip Merilees concocted Does the flap of a butterfly's wings in Brazil set off a tornado in Texas? as a title.[1] Although a butterfly flapping its wings has remained constant in the expression of this concept, the location of the butterfly, the consequences, and the location of the consequences have varied widely.[13]
The phrase refers to the idea that a butterfly's wings might create tiny changes in the atmosphere that may ultimately alter the path of a tornado or delay, accelerate, or even prevent the occurrence of a tornado in another location. The butterfly does not power or directly create the tornado, but the term is intended to imply that the flap of the butterfly's wings can cause the tornado: in the sense that the flap of the wings is a part of the initial conditions of an interconnected complex web; one set of conditions leads to a tornado, while the other set of conditions doesn't. The flapping wing represents a small change in the initial condition of the system, which cascades to large-scale alterations of events (compare: domino effect). Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different—but it's also equally possible that the set of conditions without the butterfly flapping its wings is the set that leads to a tornado.
The butterfly effect presents an obvious challenge to prediction, since initial conditions for a system such as the weather can never be known to complete accuracy. This problem motivated the development of ensemble forecasting, in which a number of forecasts are made from perturbed initial conditions.[14]
Some scientists have since argued that the weather system is not as sensitive to initial conditions as previously believed.[15] David Orrell argues that the major contributor to weather forecast error is model error, with sensitivity to initial conditions playing a relatively small role.[16][17] Stephen Wolfram also notes that the Lorenz equations are highly simplified and do not contain terms that represent viscous effects; he believes that these terms would tend to damp out small perturbations.[18] Recent studies using generalized Lorenz models that included additional dissipative terms and nonlinearity suggested that a larger heating parameter is required for the onset of chaos.[19]
While the "butterfly effect" is often explained as being synonymous with sensitive dependence on initial conditions of the kind described by Lorenz in his 1963 paper (and previously observed by Poincaré), the butterfly metaphor was originally applied[1] to work he published in 1969[20] which took the idea a step further. Lorenz proposed a mathematical model for how tiny motions in the atmosphere scale up to affect larger systems. He found that the systems in that model could only be predicted up to a specific point in the future, and beyond that, reducing the error in the initial conditions would not increase the predictability (as long as the error is not zero). This demonstrated that a deterministic system could be "observationally indistinguishable" from a non-deterministic one in terms of predictability. Recent re-examinations of this paper suggest that it offered a significant challenge to the idea that our universe is deterministic, comparable to the challenges offered by quantum physics.[21][22]
In the book entitled The Essence of Chaos published in 1993,[23] Lorenz defined butterfly effect as: "The phenomenon that a small alteration in the state of a dynamical system will cause subsequent states to differ greatly from the states that would have followed without the alteration." This feature is the same as sensitive dependence of solutions on initial conditions (SDIC) in .[3] In the same book, Lorenz applied the activity of skiing and developed an idealized skiing model for revealing the sensitivity of time-varying paths to initial positions. A predictability horizon is determined before the onset of SDIC.[24]
Illustrations
The butterfly effect in the Lorenz attractor time 0 ≤ t ≤ 30 (larger) z coordinate (larger) 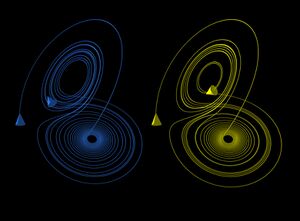
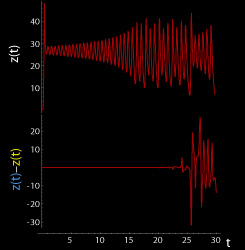
These figures show two segments of the three-dimensional evolution of two trajectories (one in blue, and the other in yellow) for the same period of time in the Lorenz attractor starting at two initial points that differ by only 10−5 in the x-coordinate. Initially, the two trajectories seem coincident, as indicated by the small difference between the z coordinate of the blue and yellow trajectories, but for t > 23 the difference is as large as the value of the trajectory. The final position of the cones indicates that the two trajectories are no longer coincident at t = 30. An animation of the Lorenz attractor shows the continuous evolution.
Theory and mathematical definition
Recurrence, the approximate return of a system toward its initial conditions, together with sensitive dependence on initial conditions, are the two main ingredients for chaotic motion. They have the practical consequence of making complex systems, such as the weather, difficult to predict past a certain time range (approximately a week in the case of weather) since it is impossible to measure the starting atmospheric conditions completely accurately.
A dynamical system displays sensitive dependence on initial conditions if points arbitrarily close together separate over time at an exponential rate. The definition is not topological, but essentially metrical. Lorenz[23] defined sensitive dependence as follows:
The property characterizing an orbit (i.e., a solution) if most other orbits that pass close to it at some point do not remain close to it as time advances.
If M is the state space for the map [math]\displaystyle{ f^t }[/math], then [math]\displaystyle{ f^t }[/math] displays sensitive dependence to initial conditions if for any x in M and any δ > 0, there are y in M, with distance d(. , .) such that [math]\displaystyle{ 0 \lt d(x, y) \lt \delta }[/math] and such that
- [math]\displaystyle{ d(f^\tau(x), f^\tau(y)) \gt \mathrm{e}^{a\tau} \, d(x,y) }[/math]
for some positive parameter a. The definition does not require that all points from a neighborhood separate from the base point x, but it requires one positive Lyapunov exponent. In addition to a positive Lyapunov exponent, boundedness is another major feature within chaotic systems.[25]
The simplest mathematical framework exhibiting sensitive dependence on initial conditions is provided by a particular parametrization of the logistic map:
- [math]\displaystyle{ x_{n+1} = 4 x_n (1-x_n) , \quad 0\leq x_0\leq 1, }[/math]
which, unlike most chaotic maps, has a closed-form solution:
- [math]\displaystyle{ x_{n}=\sin^{2}(2^{n} \theta \pi) }[/math]
where the initial condition parameter [math]\displaystyle{ \theta }[/math] is given by [math]\displaystyle{ \theta = \tfrac{1}{\pi}\sin^{-1}(x_0^{1/2}) }[/math]. For rational [math]\displaystyle{ \theta }[/math], after a finite number of iterations [math]\displaystyle{ x_n }[/math] maps into a periodic sequence. But almost all [math]\displaystyle{ \theta }[/math] are irrational, and, for irrational [math]\displaystyle{ \theta }[/math], [math]\displaystyle{ x_n }[/math] never repeats itself – it is non-periodic. This solution equation clearly demonstrates the two key features of chaos – stretching and folding: the factor 2n shows the exponential growth of stretching, which results in sensitive dependence on initial conditions (the butterfly effect), while the squared sine function keeps [math]\displaystyle{ x_n }[/math] folded within the range [0, 1].
In physical systems
In weather
The butterfly effect is most familiar in terms of weather; it can easily be demonstrated in standard weather prediction models, for example. The climate scientists James Annan and William Connolley explain that chaos is important in the development of weather prediction methods; models are sensitive to initial conditions. They add the caveat: "Of course the existence of an unknown butterfly flapping its wings has no direct bearing on weather forecasts, since it will take far too long for such a small perturbation to grow to a significant size, and we have many more immediate uncertainties to worry about. So the direct impact of this phenomenon on weather prediction is often somewhat wrong."[26] The two kinds of butterfly effects, including the sensitive dependence on initial conditions,[3] and the ability of a tiny perturbation to create an organized circulation at large distances,[1] are not exactly the same.[27] A comparison of the two kinds of butterfly effects[1][3] and the third kind of butterfly effect[20][21][22] has been documented.[28] In recent studies,[24][29] it was reported that both meteorological and non-meteorological linear models have shown that instability plays a role in producing a butterfly effect, which is characterized by brief but significant exponential growth resulting from a small disturbance.
According to Lighthill (1986),[30] the presence of SDIC (commonly known as the butterfly effect) implies that chaotic systems have a finite predictability limit. In a literature review,[31] it was found that Lorenz's perspective on the predictability limit can be condensed into the following statement:
- (A). The Lorenz 1963 model qualitatively revealed the essence of a finite predictability within a chaotic system such as the atmosphere. However, it did not determine a precise limit for the predictability of the atmosphere.
- (B). In the 1960s, the two-week predictability limit was originally estimated based on a doubling time of five days in real-world models. Since then, this finding has been documented in Charney et al. (1966)[32][33] and has become a consensus.
Recently, a short video has been created to present Lorenz's perspective on predictability limit.[34]
By revealing coexisting chaotic and non-chaotic attractors within Lorenz models, Shen and his colleagues proposed a revised view that "weather possesses chaos and order", in contrast to the conventional view of "weather is chaotic".[35][36][37] As a result, sensitive dependence on initial conditions (SDIC) does not always appear. Namely, SDIC appears when two orbits (i.e., solutions) become the chaotic attractor; it does not appear when two orbits move toward the same point attractor. The above animation for double pendulum motion provides an analogy. For large angles of swing the motion of the pendulum is often chaotic.[38][39] By comparison, for small angles of swing, motions are non-chaotic.
Multistability is defined when a system (e.g., the double pendulum system) contains more than one bounded attractor that depends only on initial conditions. The multistability was illustrated using kayaking in Figure on the right side (i.e., Figure 1 of [40]) where the appearance of strong currents and a stagnant area suggests instability and local stability, respectively. As a result, when two kayaks move along strong currents, their paths display SDIC. On the other hand, when two kayaks move into a stagnant area, they become trapped, showing no typical SDIC (although a chaotic transient may occur). Such features of SDIC or no SDIC suggest two types of solutions and illustrate the nature of multistability.
By taking into consideration time-varying multistability that is associated with the modulation of large-scale processes (e.g., seasonal forcing) and aggregated feedback of small-scale processes (e.g., convection), the above revised view is refined as follows:
"The atmosphere possesses chaos and order; it includes, as examples, emerging organized systems (such as tornadoes) and time varying forcing from recurrent seasons."[40][41]
In quantum mechanics
The potential for sensitive dependence on initial conditions (the butterfly effect) has been studied in a number of cases in semiclassical and quantum physics including atoms in strong fields and the anisotropic Kepler problem.[42][43] Some authors have argued that extreme (exponential) dependence on initial conditions is not expected in pure quantum treatments;[44][45] however, the sensitive dependence on initial conditions demonstrated in classical motion is included in the semiclassical treatments developed by Martin Gutzwiller[46] and John B. Delos and co-workers.[47] The random matrix theory and simulations with quantum computers prove that some versions of the butterfly effect in quantum mechanics do not exist.[48]
Other authors suggest that the butterfly effect can be observed in quantum systems. Zbyszek P. Karkuszewski et al. consider the time evolution of quantum systems which have slightly different Hamiltonians. They investigate the level of sensitivity of quantum systems to small changes in their given Hamiltonians.[49] David Poulin et al. presented a quantum algorithm to measure fidelity decay, which "measures the rate at which identical initial states diverge when subjected to slightly different dynamics". They consider fidelity decay to be "the closest quantum analog to the (purely classical) butterfly effect".[50] Whereas the classical butterfly effect considers the effect of a small change in the position and/or velocity of an object in a given Hamiltonian system, the quantum butterfly effect considers the effect of a small change in the Hamiltonian system with a given initial position and velocity.[51][52] This quantum butterfly effect has been demonstrated experimentally.[53] Quantum and semiclassical treatments of system sensitivity to initial conditions are known as quantum chaos.[44][51]
In popular culture
See also
- Avalanche effect
- Behavioral cusp
- Cascading failure
- Catastrophe theory
- Causality
- Chain reaction
- Clapotis
- Determinism
- Domino effect
- Dynamical system
- Fractal
- Great Stirrup Controversy
- Innovation butterfly
- Kessler syndrome
- Norton's dome
- Numerical analysis
- Point of divergence
- Positive feedback
- Potentiality and actuality
- Representativeness heuristic
- Ripple effect
- Snowball effect
- Traffic congestion
- Tropical cyclogenesis
- Unintended consequences
References
- ↑ 1.0 1.1 1.2 1.3 1.4 "Predictability: Does the Flap of a Butterfly's Wings in Brazil Set Off a Tornado in Texas?". https://mathsciencehistory.com/wp-content/uploads/2020/03/132_kap6_lorenz_artikel_the_butterfly_effect.pdf.
- ↑ "When Lorenz Discovered the Butterfly Effect". 22 May 2015. https://www.bbvaopenmind.com/en/science/leading-figures/when-lorenz-discovered-the-butterfly-effect/.
- ↑ 3.0 3.1 3.2 3.3 3.4 Lorenz, Edward N. (March 1963). "Deterministic Nonperiodic Flow". Journal of the Atmospheric Sciences 20 (2): 130–141. doi:10.1175/1520-0469(1963)020<0130:dnf>2.0.co;2. Bibcode: 1963JAtS...20..130L.
- ↑ Rouvas-Nicolis, Catherine; Nicolis, Gregoire (4 May 2009). "Butterfly effect". Scholarpedia. 4. p. 1720. doi:10.4249/scholarpedia.1720. Bibcode: 2009SchpJ...4.1720R. http://www.scholarpedia.org/article/Butterfly_effect. Retrieved 2016-01-02.
- ↑ 5.0 5.1 Some Historical Notes: History of Chaos Theory
- ↑ Steves, Bonnie; Maciejewski, AJ (September 2001). The Restless Universe Applications of Gravitational N-Body Dynamics to Planetary Stellar and Galactic Systems. USA: CRC Press. ISBN 0750308222. https://books.google.com/books?id=-wa120qRW5wC. Retrieved January 6, 2014.
- ↑ Computing Machinery and Intelligence
- ↑ Flam, Faye (2012-06-15). "The Physics of Ray Bradbury's "A Sound of Thunder"". The Philadelphia Inquirer. https://www.inquirer.com/philly/blogs/evolution/Time-and-The-Physics-of-Ray-Bradbury--.html.
- ↑ Gleick, James (1987). Chaos: Making a New Science. Viking. p. 16. ISBN 0-8133-4085-3.
- ↑ Google Scholar citation record
- ↑ "Part19". Cs.ualberta.ca. 1960-11-22. http://www.cs.ualberta.ca/~smillie/ComputerAndMe/Part19.html.
- ↑ 12.0 12.1 Lorenz, Edward N. (1963). "The Predictability of Hydrodynamic Flow". Transactions of the New York Academy of Sciences 25 (4): 409–432. doi:10.1111/j.2164-0947.1963.tb01464.x. https://eapsweb.mit.edu/sites/default/files/Predictability_hydrodynamic_flow_1963.pdf. Retrieved 1 September 2014.
- ↑ "The Butterfly Effects: Variations on a Meme". AP42 ...and everything. http://blog.ap42.com/2011/08/03/the-butterfly-effect-variations-on-a-meme/.
- ↑ Woods, Austin (2005). Medium-range weather prediction: The European approach; The story of the European Centre for Medium-Range Weather Forecasts. New York: Springer. p. 118. ISBN 978-0387269283. https://archive.org/details/mediumrangeweath00wood.
- ↑ Orrell, David; Smith, Leonard; Barkmeijer, Jan; Palmer, Tim (2001). "Model error in weather forecasting". Nonlinear Processes in Geophysics 9 (6): 357–371. doi:10.5194/npg-8-357-2001. Bibcode: 2001NPGeo...8..357O.
- ↑ Orrell, David (2002). "Role of the metric in forecast error growth: How chaotic is the weather?". Tellus 54A (4): 350–362. doi:10.3402/tellusa.v54i4.12159. Bibcode: 2002TellA..54..350O.
- ↑ Orrell, David (2012). Truth or Beauty: Science and the Quest for Order. New Haven: Yale University Press. p. 208. ISBN 978-0300186611.
- ↑ Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media. p. 998. ISBN 978-1579550080. https://archive.org/details/newkindofscience00wolf.
- ↑ Shen, Bo-Wen (2019). "Aggregated Negative Feedback in a Generalized Lorenz Model". International Journal of Bifurcation and Chaos 29 (3): 1950037–1950091. doi:10.1142/S0218127419500378. Bibcode: 2019IJBC...2950037S.
- ↑ 20.0 20.1 Lorenz, Edward N. (June 1969). "The predictability of a flow which possesses many scales of motion". Tellus XXI (3): 289–297. doi:10.1111/j.2153-3490.1969.tb00444.x. Bibcode: 1969Tell...21..289L.
- ↑ 21.0 21.1 Tim, Palmer (19 May 2017). "The Butterfly Effect – What Does It Really Signify?". https://www.youtube.com/watch?v=vkQEqXAz44I.
- ↑ 22.0 22.1 Emanuel, Kerry (26 March 2018). "Edward N. Lorenz and the End of the Cartesian Universe". https://www.youtube.com/watch?v=FvWeK_PfDE4.
- ↑ 23.0 23.1 Lorenz, Edward N. (1993). The essence of chaos. London: UCL Press. ISBN 0-203-21458-7. OCLC 56620850. https://www.worldcat.org/oclc/56620850.
- ↑ 24.0 24.1 Shen, Bo-Wen; Pielke, Roger A.; Zeng, Xubin (2022-05-07). "One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models". Atmosphere 13 (5): 753. doi:10.3390/atmos13050753. ISSN 2073-4433. Bibcode: 2022Atmos..13..753S.
- ↑ W., Jordan, Dominic (2011). Nonlinear ordinary differential equations: an introduction for scientists and engineers. Oxford Univ. Press. ISBN 978-0-19-920825-8. OCLC 772641393. https://www.worldcat.org/oclc/772641393.
- ↑ "Chaos and Climate". RealClimate. 4 November 2005. https://www.realclimate.org/index.php/archives/2005/11/chaos-and-climate/.
- ↑ Shen, Bo-Wen (2014-05-01). "Nonlinear Feedback in a Five-Dimensional Lorenz Model" (in EN). Journal of the Atmospheric Sciences 71 (5): 1701–1723. doi:10.1175/JAS-D-13-0223.1. ISSN 0022-4928. Bibcode: 2014JAtS...71.1701S. https://journals.ametsoc.org/view/journals/atsc/71/5/jas-d-13-0223.1.xml.
- ↑ Shen, Bo-Wen; Pielke, Roger A.; Zeng, Xubin; Cui, Jialin; Faghih-Naini, Sara; Paxson, Wei; Atlas, Robert (2022-07-04). "Three Kinds of Butterfly Effects within Lorenz Models" (in en). Encyclopedia 2 (3): 1250–1259. doi:10.3390/encyclopedia2030084. ISSN 2673-8392.
- ↑ Saiki, Yoshitaka; Yorke, James A. (2023-05-02). "Can the Flap of a Butterfly's Wings Shift a Tornado into Texas—Without Chaos?" (in en). Atmosphere 14 (5): 821. doi:10.3390/atmos14050821. ISSN 2073-4433. Bibcode: 2023Atmos..14..821S.
- ↑ Lighthill, James (1986-09-08). "The recently recognized failure of predictability in Newtonian dynamics". Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 407 (1832): 35–50. doi:10.1098/rspa.1986.0082. ISSN 0080-4630. Bibcode: 1986RSPSA.407...35L. http://dx.doi.org/10.1098/rspa.1986.0082.
- ↑ Shen, Bo-Wen; Pielke, Roger A.; Zeng, Xubin; Zeng, Xiping (2023-07-22). "Lorenz's View on the Predictability Limit of the Atmosphere" (in en). Encyclopedia 3 (3): 887–899. doi:10.3390/encyclopedia3030063. ISSN 2673-8392.
 This article incorporates text from this source, which is available under the CC BY 4.0 license.
This article incorporates text from this source, which is available under the CC BY 4.0 license.
- ↑ The Feasibility of a Global Observation and Analysis Experiment. 1966-01-01. doi:10.17226/21272. ISBN 978-0-309-35922-1. http://dx.doi.org/10.17226/21272.
- ↑ GARP (1969-03-01). "A Guide to GARP". Bull. Amer. Meteor. Soc. 50 (3): 136–141. doi:10.1175/1520-0477-50.3.136. Bibcode: 1969BAMS...50..136..
- ↑ Shen, Bo-Wen; Pielke, Sr., Roger; Zeng, Xubin; Zeng, Xiping (2023-09-13). "Lorenz's View on the Predictability Limit.". https://encyclopedia.pub/video/video_detail/916.
- ↑ Shen, Bo-Wen; Pielke, Roger A.; Zeng, Xubin; Baik, Jong-Jin; Faghih-Naini, Sara; Cui, Jialin; Atlas, Robert (2021-01-01). "Is Weather Chaotic?: Coexistence of Chaos and Order within a Generalized Lorenz Model" (in EN). Bulletin of the American Meteorological Society 102 (1): E148–E158. doi:10.1175/BAMS-D-19-0165.1. ISSN 0003-0007. Bibcode: 2021BAMS..102E.148S.
- ↑ Shen, Bo-Wen; Pielke, R. A. Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R.; Reyes, T. A. L. (2021). "Is Weather Chaotic? Coexisting Chaotic and Non-chaotic Attractors within Lorenz Models". in Skiadas, Christos H.; Dimotikalis, Yiannis (in en). 13th Chaotic Modeling and Simulation International Conference. Springer Proceedings in Complexity. Cham: Springer International Publishing. pp. 805–825. doi:10.1007/978-3-030-70795-8_57. ISBN 978-3-030-70795-8. https://link.springer.com/chapter/10.1007/978-3-030-70795-8_57.
- ↑ Anthes, Richard A. (2022-08-14). "Predictability and Predictions" (in en). Atmosphere 13 (8): 1292. doi:10.3390/atmos13081292. ISSN 2073-4433. Bibcode: 2022Atmos..13.1292A.
- ↑ Richter, P. H.; Scholz, H.-J. (1984), "Chaos in Classical Mechanics: The Double Pendulum", Stochastic Phenomena and Chaotic Behaviour in Complex Systems, Springer Series in Synergetics (Berlin, Heidelberg: Springer Berlin Heidelberg) 21: pp. 86–97, doi:10.1007/978-3-642-69591-9_9, ISBN 978-3-642-69593-3, https://link.springer.com/chapter/10.1007/978-3-642-69591-9_9, retrieved 2022-07-11
- ↑ Shinbrot, Troy, Celso A Grebogi, Jack Wisdom, James A Yorke (1992). "Chaos in a double pendulum". American Journal of Physics 60 (6): 491–499. doi:10.1119/1.16860. Bibcode: 1992AmJPh..60..491S. https://doi.org/10.1119/1.16860.
- ↑ 40.0 40.1 Shen, Bo-Wen; Pielke Sr., Roger Pielke; Zeng, Xubin; Cui, Jialin; Faghih-Naini, Sara; Paxson, Wei; Kesarkar, Amit; Zeng, Xiping et al. (2022-11-12). "The Dual Nature of Chaos and Order in the Atmosphere" (in en). Atmosphere 13 (11): 1892. doi:10.3390/atmos13111892. ISSN 2073-4433. Bibcode: 2022Atmos..13.1892S.
 Text was copied from this source, which is available under a Creative Commons Attribution 4.0 International License.
Text was copied from this source, which is available under a Creative Commons Attribution 4.0 International License.
- ↑ Shen, Bo-Wen (21 Feb 2023). "Exploring Chaos Theory for Monstability and Multistability". https://www.youtube.com/watch?v=GXtpkf3QsPI.
- ↑ Heller, E. J.; Tomsovic, S. (July 1993). "Postmodern Quantum Mechanics". Physics Today 46 (7): 38–46. doi:10.1063/1.881358. Bibcode: 1993PhT....46g..38H.
- ↑ Gutzwiller, Martin C. (1990). Chaos in Classical and Quantum Mechanics. New York: Springer-Verlag. ISBN 0-387-97173-4.
- ↑ 44.0 44.1 Rudnick, Ze'ev (January 2008). "What is... Quantum Chaos?". Notices of the American Mathematical Society. https://www.ams.org/notices/200801/tx080100032p.pdf.
- ↑ Berry, Michael (1989). "Quantum chaology, not quantum chaos". Physica Scripta 40 (3): 335–336. doi:10.1088/0031-8949/40/3/013. Bibcode: 1989PhyS...40..335B.
- ↑ Gutzwiller, Martin C. (1971). "Periodic Orbits and Classical Quantization Conditions". Journal of Mathematical Physics 12 (3): 343. doi:10.1063/1.1665596. Bibcode: 1971JMP....12..343G.
- ↑ Gao, J.; Delos, J. B. (1992). "Closed-orbit theory of oscillations in atomic photoabsorption cross sections in a strong electric field. II. Derivation of formulas". Physical Review A 46 (3): 1455–1467. doi:10.1103/PhysRevA.46.1455. PMID 9908268. Bibcode: 1992PhRvA..46.1455G. https://scholarworks.wm.edu/cgi/viewcontent.cgi?article=2818&context=aspubs.
- ↑ Yan, Bin; Sinitsyn, Nikolai A. (2020). "Recovery of Damaged Information and the Out-of-Time-Ordered Correlators". Physical Review Letters 125 (4): 040605. doi:10.1103/PhysRevLett.125.040605. PMID 32794812. Bibcode: 2020PhRvL.125d0605Y.
- ↑ Karkuszewski, Zbyszek P.; Jarzynski, Christopher; Zurek, Wojciech H. (2002). "Quantum Chaotic Environments, the Butterfly Effect, and Decoherence". Physical Review Letters 89 (17): 170405. doi:10.1103/PhysRevLett.89.170405. PMID 12398653. Bibcode: 2002PhRvL..89q0405K.
- ↑ Poulin, David; Blume-Kohout, Robin; Laflamme, Raymond; Ollivier, Harold (2004). "Exponential Speedup with a Single Bit of Quantum Information: Measuring the Average Fidelity Decay". Physical Review Letters 92 (17): 177906. doi:10.1103/PhysRevLett.92.177906. PMID 15169196. Bibcode: 2004PhRvL..92q7906P.
- ↑ 51.0 51.1 Poulin, David. "A Rough Guide to Quantum Chaos". http://www.iqc.ca/publications/tutorials/chaos.pdf.
- ↑ Peres, A. (1995). Concepts and Methods. Dordrecht: Kluwer Academic.
- ↑ Lee, Jae-Seung; Khitrin, A. K. (2004). "Quantum amplifier: Measurement with entangled spins". Journal of Chemical Physics 121 (9): 3949–51. doi:10.1063/1.1788661. PMID 15332940. Bibcode: 2004JChPh.121.3949L.
Further reading
- James Gleick, Making a New Science, New York: Viking, 1987. 368 pp.
- Devaney, Robert L. (2003). Introduction to Chaotic Dynamical Systems. Westview Press. ISBN 0670811785.
- Hilborn, Robert C. (2004). "Sea gulls, butterflies, and grasshoppers: A brief history of the butterfly effect in nonlinear dynamics". American Journal of Physics 72 (4): 425–427. doi:10.1119/1.1636492. Bibcode: 2004AmJPh..72..425H.
- Bradbury, Ray. "A Sound of Thunder." Collier's. 28 June 1952
External links
- Weather and Chaos: The Work of Edward N. Lorenz. A short documentary that explains the "butterfly effect" in context of Lorenz's work.
- The Chaos Hypertextbook. An introductory primer on chaos and fractals
- Dizikes, Peter (2008-06-08). "The meaning of the butterfly. Why pop culture loves the 'butterfly effect,' and gets it totally wrong.". The Boston Globe (Boston, Massachusetts). http://archive.boston.com/bostonglobe/ideas/articles/2008/06/08/the_meaning_of_the_butterfly/.
- New England Complex Systems Institute - Concepts: Butterfly Effect
- ChaosBook.org. Advanced graduate textbook on chaos (no fractals)
- Weisstein, Eric W.. "Butterfly Effect". http://mathworld.wolfram.com/ButterflyEffect.html.
 |



