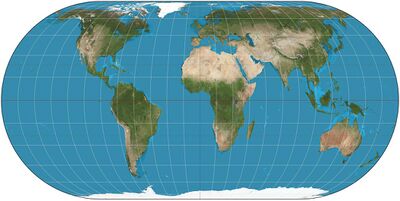
Eckert IV projection
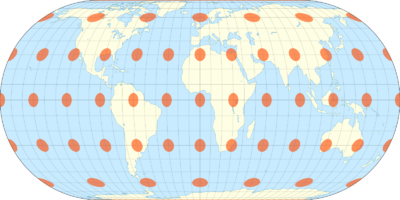
The Eckert IV projection is an equal-area pseudocylindrical map projection. The length of the polar lines is half that of the equator, and lines of longitude are semiellipses, or portions of ellipses. It was first described by Max Eckert in 1906 as one of a series of three pairs of pseudocylindrical projections. Within each pair, meridians are the same whereas parallels differ. Odd-numbered projections have parallels spaced equally, whereas even-numbered projections have parallels spaced to preserve area. Eckert IV is paired with Eckert III.[1]
Formulas
Forward formulae
Given a sphere of radius R, central meridian λ0 and a point with geographical latitude φ and longitude λ, plane coordinates x and y can be computed using the following formulas:
- [math]\displaystyle{ \begin{align} x & = \frac{2}{\sqrt{4\pi + \pi^2}} R\, (\lambda - \lambda_0)(1 + \cos \theta) \approx 0.422\,2382\, R\, (\lambda - \lambda_0)(1 + \cos \theta), \\[8pt] y & = 2 \sqrt{\frac{\pi}{4 + \pi}} R \sin \theta \approx 1.326\,5004\, R \sin \theta, \end{align} }[/math]
where
- [math]\displaystyle{ \theta + \sin \theta \cos \theta + 2 \sin \theta = \left(2 + \frac \pi 2\right) \sin \varphi. }[/math]
θ can be solved for numerically using Newton's method.[2]
Inverse formulae
- [math]\displaystyle{ \begin{align} \theta & = \arcsin \left[y \frac{\sqrt{4 + \pi}}{2 \sqrt\pi R}\right] \approx \arcsin \left[\frac{y}{1.326\,5004\, R}\right] \\[8pt] \varphi & = \arcsin \left[\frac{\theta + \sin \theta \cos \theta + 2 \sin \theta}{2 + \frac \pi 2}\right] \\[8pt] \lambda & = \lambda_0 + x \frac{\sqrt{4\pi + \pi^2}}{2R (1 + \cos \theta)} \approx \lambda_0 + \frac{x}{0.422\,2382\, R\, (1 + \cos \theta)} \end{align} }[/math]
See also
- List of map projections
- Eckert II projection
- Eckert VI projection
- Max Eckert-Greifendorff
References
- ↑ Snyder, John P.; Voxland, Philip M. (1989). An Album of Map Projections. Professional Paper 1453. Denver: USGS. pp. 60. ISBN 978-0160033681. https://pubs.er.usgs.gov/usgspubs/pp/pp1453. Retrieved 2014-09-27.
- ↑ Snyder, John P. (1987). Map Projections – A Working Manual. Professional Paper 1395. Denver: USGS. pp. 253–258. ISBN 0-226-76747-7. https://pubs.er.usgs.gov/usgspubs/pp/pp1395. Retrieved 2013-07-24.
External links
 |