Cylindrical equal-area projection

Short description: Family of map projections

Lambert cylindrical equal-area projection of the world; standard parallel at 0°

The Lambert (standard parallel at 0°, normal) cylindrical equal-area projection with Tissot's indicatrix of deformation

In cartography, the normal cylindrical equal-area projection is a family of normal cylindrical, equal-area map projections.

History

The invention of the Lambert cylindrical equal-area projection is attributed to the Switzerland mathematician Johann Heinrich Lambert in 1772. Variations of it appeared over the years by inventors who stretched the height of the Lambert and compressed the width commensurately in various ratios.

Description

How the Earth is projected onto a cylinder

The projection:

• is cylindrical, that means it has a cylindrical projection surface
• is normal, that means it has a normal aspect
• is an equal-area projection, that means any two areas in the map have the same relative size compared to their size on the sphere.

The term "normal cylindrical projection" is used to refer to any projection in which meridians are mapped to equally spaced vertical lines and circles of latitude are mapped to horizontal lines (or, mutatis mutandis, more generally, radial lines from a fixed point are mapped to equally spaced parallel lines and concentric circles around it are mapped to perpendicular lines).

The mapping of meridians to vertical lines can be visualized by imagining a cylinder whose axis coincides with the Earth's axis of rotation, then projecting onto the cylinder, and subsequently unfolding the cylinder.

By the geometry of their construction, cylindrical projections stretch distances east-west. The amount of stretch is the same at any chosen latitude on all cylindrical projections, and is given by the secant of the latitude as a multiple of the equator's scale. The various cylindrical projections are distinguished from each other solely by their north-south stretching (where latitude is given by φ):

The only normal cylindrical projections that preserve area have a north-south compression precisely the reciprocal of east-west stretching (cos φ). This divides north-south distances by a factor equal to the secant of the latitude, preserving area but distorting shapes.

East–west scale matching the north–south scale

Depending on the stretch factor S, any particular cylindrical equal-area projection either has zero, one or two latitudes for which the east–west scale matches the north–south scale.

• S>1 : zero
• S=1 : one, that latitude is the equator
• S<1 : a pair of identical latitudes of opposite sign

Formulae

The formulae presume a spherical model and use these definitions:

• λ is the longitude
• λ₀ is the central meridian
• φ is the latitude
• φ₀ is the standard latitude
• S is the stretch factor
• x is the horizontal coordinate of the projected location on the map
• y is the vertical coordinate of the projected location on the map

Except for the Lambrecht case one of φ₀ and S has to be provided.

	using standard latitude φ0	using stretch factor S	S=1, φ0=0
using radians	[math]\displaystyle{ \begin{align}x &= ( \lambda - \lambda_0 ) \cos \varphi_0 \\ y &= \frac{\sin \varphi}{\cos \varphi_0}\end{align} }[/math]	[math]\displaystyle{ \begin{align}x &= ( \lambda - \lambda_0 ) S \\ y &= \sin\varphi\end{align} }[/math]	[math]\displaystyle{ \begin{align}x &= \lambda - \lambda_0\\ y &= \sin \varphi\end{align} }[/math]
using degrees	[math]\displaystyle{ \begin{align}x &= \frac{\pi ( \lambda - \lambda_0 ) \cos\varphi_0}{180^\circ}\\ y &= \frac{\sin \varphi}{\cos \varphi_0}\end{align} }[/math]

Relationship between S and φ₀:

• S = (cos φ₀)²
• φ₀ = arccos(S^0.5)

Specializations

The specializations differ only in the ratio of the vertical to horizontal axis. Some specializations have been described, promoted, or otherwise named.

Specializations of the normal cylindrical equal-area projection, images showing projection centered on the Greenwich meridian

Stretch factor S	Aspect ratio (width-to-height) πS	Standard parallel(s) φ0	Image (Tissot's indicatrix)	Image (Blue Marble)	Name	Publisher	Year of publication
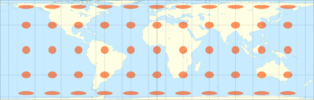
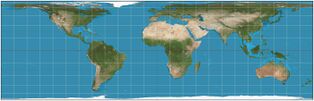
1	π ≈ 3.142	0°			Lambert cylindrical equal-area	Johann Heinrich Lambert	1772
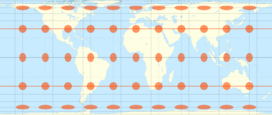
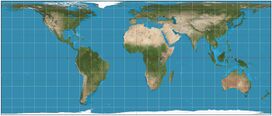
3/4 = 0.75	3π/4 ≈ 2.356	30°			Behrmann	Walter Behrmann	1910
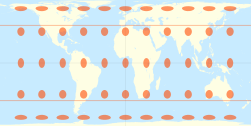
2/π ≈ 0.6366	2	[math]\displaystyle{ \arccos \sqrt{\tfrac{2}{\pi}} }[/math] ≈ 37°04′17″ ≈ 37.0714°			Smyth equal-surface = Craster rectangular	Charles Piazzi Smyth	1870
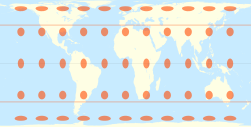
cos2(37.4°) ≈ 0.6311	π·cos2(37.4°) ≈ 1.983	37°24′ = 37.4°			Trystan Edwards	Trystan Edwards	1953
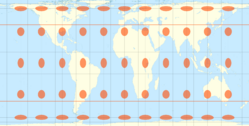
cos2(37.5°) ≈ 0.6294	π·cos2(37.5°) ≈ 1.977	37°30′ = 37.5°			Hobo–Dyer	Mick Dyer	2002
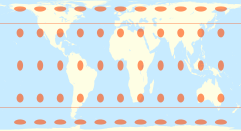
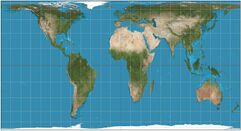
cos2(40°) ≈ 0.5868	π·cos2(40°) ≈ 1.844	40°			(unnamed)
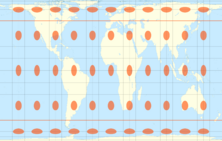
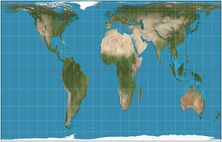
1/2 =0.5	π/2 ≈ 1.571	45°			Gall–Peters = Gall orthographic = Peters	James Gall, Promoted by Arno Peters as his own invention	1855 (Gall), 1967 (Peters)
cos2(50°) ≈ 0.4132	π·cos2(50°) ≈ 1.298	50°		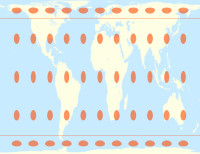	Balthasart	M. Balthasart	1935
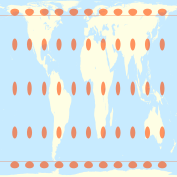
1/π ≈ 0.3183	1	[math]\displaystyle{ \arccos \sqrt{\tfrac{1}{\pi}} }[/math] ≈ 55°39′14″ ≈ 55.6540°			Tobler's world in a square	Waldo Tobler	1986

Derivatives

The Tobler hyperelliptical projection, first described by Tobler in 1973, is a further generalization of the cylindrical equal-area family.

The HEALPix projection is an equal-area hybrid combination of: the Lambert cylindrical equal-area projection, for the equatorial regions of the sphere; and an interrupted Collignon projection, for the polar regions.

External links

• Table of examples and properties of all common projections, from radicalcartography.net