Barycentric coordinate system
In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex (a triangle for points in a plane, a tetrahedron for points in three-dimensional space, etc.). The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass (or barycenter) of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex.
Every point has barycentric coordinates, and their sum is not zero. Two tuples of barycentric coordinates specify the same point if and only if they are proportional; that is to say, if one tuple can be obtained by multiplying the elements of the other tuple by the same non-zero number. Therefore, barycentric coordinates are either considered to be defined up to multiplication by a nonzero constant, or normalized for summing to unity.
Barycentric coordinates were introduced by August Möbius in 1827.[1][2][3] They are special homogenous coordinates. Barycentric coordinates are strongly related with Cartesian coordinates and, more generally, to affine coordinates (see Affine space § Relationship between barycentric and affine coordinates).
Barycentric coordinates are particularly useful in triangle geometry for studying properties that do not depend on the angles of the triangle, such as Ceva's theorem, Routh's theorem, and Menelaus's theorem. In computer-aided design, they are useful for defining some kinds of Bézier surfaces.[4][5]
Definition
Let [math]\displaystyle{ A_0, \ldots, A_n }[/math] be n + 1 points in a Euclidean space, a flat or an affine space [math]\displaystyle{ \mathbf A }[/math] of dimension n that are affinely independent; this means that there is no affine subspace of dimension n - 1 that contains all the points,[6] or, equivalently that the points define a simplex. Given any point [math]\displaystyle{ P\in \mathbf A, }[/math] there are scalars [math]\displaystyle{ a_0, \ldots, a_n }[/math] that are not all zero, such that [math]\displaystyle{ ( a_0 + \cdots + a_n ) \overrightarrow{OP} = a_0 \overrightarrow {OA_0} + \cdots + a_n \overrightarrow {OA_n}, }[/math] for any point O. (As usual, the notation [math]\displaystyle{ \overrightarrow {AB} }[/math] represents the translation vector or free vector that maps the point A to the point B.)
The elements of a (n + 1) tuple [math]\displaystyle{ (a_0: \dotsc: a_n) }[/math] that satisfies this equation are called barycentric coordinates of P with respect to [math]\displaystyle{ A_0, \ldots, A_n. }[/math] The use of colons in the notation of the tuple means that barycentric coordinates are a sort of homogeneous coordinates, that is, the point is not changed if all coordinates are multiplied by the same nonzero constant. Moreover, the barycentric coordinates are also not changed if the auxiliary point O, the origin, is changed.
The barycentric coordinates of a point are unique up to a scaling. That is, two tuples [math]\displaystyle{ (a_0: \dotsc: a_n) }[/math] and [math]\displaystyle{ (b_0: \dotsc: b_n) }[/math] are barycentric coordinates of the same point if and only if there is a nonzero scalar [math]\displaystyle{ \lambda }[/math] such that [math]\displaystyle{ b_i=\lambda a_i }[/math] for every i.
In some contexts, it is useful to constrain the barycentric coordinates of a point so that they are unique. This is usually achieved by imposing the condition [math]\displaystyle{ \sum a_i = 1, }[/math] or equivalently by dividing every [math]\displaystyle{ a_i }[/math] by the sum of all [math]\displaystyle{ a_i. }[/math] These specific barycentric coordinates are called normalized or absolute barycentric coordinates.[7] Sometimes, they are also called affine coordinates, although this term refers commonly to a slightly different concept.
Sometimes, it is the normalized barycentric coordinates that are called barycentric coordinates. In this case the above defined coordinates are called homogeneous barycentric coordinates.
With above notation, the homogeneous barycentric coordinates of Ai are all zero, except the one of index i. When working over the real numbers (the above definition is also used for affine spaces over an arbitrary field), the points whose all normalized barycentric coordinates are nonnegative form the convex hull of [math]\displaystyle{ \{A_0, \ldots, A_n\}, }[/math] which is the simplex that has these points as its vertices.
With above notation, a tuple [math]\displaystyle{ (a_1, \ldots, a_n) }[/math] such that [math]\displaystyle{ \sum_{i=0}^n a_i=0 }[/math] does not define any point, but the vector [math]\displaystyle{ a_0 \overrightarrow {OA_0} + \cdots + a_n \overrightarrow {OA_n} }[/math] is independent from the origin O. As the direction of this vector is not changed if all [math]\displaystyle{ a_i }[/math] are multiplied by the same scalar, the homogeneous tuple [math]\displaystyle{ (a_0: \dotsc: a_n) }[/math] defines a direction of lines, that is a point at infinity. See below for more details.
Relationship with Cartesian or affine coordinates
Barycentric coordinates are strongly related to Cartesian coordinates and, more generally, affine coordinates. For a space of dimension n, these coordinate systems are defined relative to a point O, the origin, whose coordinates are zero, and n points [math]\displaystyle{ A_1, \ldots, A_n, }[/math] whose coordinates are zero except that of index i that equals one.
A point has coordinates [math]\displaystyle{ (x_1, \ldots, x_n) }[/math] for such a coordinate system if and only if its normalized barycentric coordinates are [math]\displaystyle{ (1-x_1-\cdots - x_n,x_1, \ldots, x_n) }[/math] relatively to the points [math]\displaystyle{ O, A_1, \ldots, A_n. }[/math]
The main advantage of barycentric coordinate systems is to be symmetric with respect to the n + 1 defining points. They are therefore often useful for studying properties that are symmetric with respect to n + 1 points. On the other hand, distances and angles are difficult to express in general barycentric coordinate systems, and when they are involved, it is generally simpler to use a Cartesian coordinate system.
Relationship with projective coordinates
Homogeneous barycentric coordinates are also strongly related with some projective coordinates. However this relationship is more subtle than in the case of affine coordinates, and, for being clearly understood, requires a coordinate-free definition of the projective completion of an affine space, and a definition of a projective frame.
The projective completion of an affine space of dimension n is a projective space of the same dimension that contains the affine space as the complement of a hyperplane. The projective completion is unique up to an isomorphism. The hyperplane is called the hyperplane at infinity, and its points are the points at infinity of the affine space.[8]
Given a projective space of dimension n, a projective frame is an ordered set of n + 2 points that are not contained in the same hyperplane. A projective frame defines a projective coordinate system such that the coordinates of the (n + 2)th point of the frame are all equal, and, otherwise, all coordinates of the ith point are zero, except the ith one.[8]
When constructing the projective completion from an affine coordinate system, one defines commonly it with respect to a projective frame consisting of the intersections with the hyperplane at infinity of the coordinate axes, the origin of the affine space, and the point that has all its affine coordinates equal to one. This implies that the points at infinity have their last coordinate equal to zero, and that the projective coordinates of a point of the affine space are obtained by completing its affine coordinates by one as (n + 1)th coordinate.
When one has n + 1 points in an affine space that define a barycentric coordinate system, this is another projective frame of the projective completion that is convenient to choose. This frame consists of these points and their centroid, that is the point that has all its barycentric coordinates equal. In this case, the homogeneous barycentric coordinates of a point in the affine space are the same as the projective coordinates of this point. A point is at infinity if and only if the sum of its coordinates is zero. This point is in the direction of the vector defined at the end of § Definition.
Barycentric coordinates on triangles
File:TriangleBarycentricCoordinates.svg In the context of a triangle, barycentric coordinates are also known as area coordinates or areal coordinates, because the coordinates of P with respect to triangle ABC are equivalent to the (signed) ratios of the areas of PBC, PCA and PAB to the area of the reference triangle ABC. Areal and trilinear coordinates are used for similar purposes in geometry.
Barycentric or areal coordinates are extremely useful in engineering applications involving triangular subdomains. These make analytic integrals often easier to evaluate, and Gaussian quadrature tables are often presented in terms of area coordinates.
Consider a triangle [math]\displaystyle{ T }[/math] defined by its three vertices, [math]\displaystyle{ \mathbf{r}_1 }[/math], [math]\displaystyle{ \mathbf{r}_2 }[/math] and [math]\displaystyle{ \mathbf{r}_3 }[/math]. Each point [math]\displaystyle{ \mathbf{r} }[/math] located inside this triangle can be written as a unique convex combination of the three vertices. In other words, for each [math]\displaystyle{ \mathbf{r} }[/math] there is a unique sequence of three numbers, [math]\displaystyle{ \lambda_1,\lambda_2,\lambda_3\geq 0 }[/math] such that [math]\displaystyle{ \lambda_1+\lambda_2+\lambda_3=1 }[/math] and
[math]\displaystyle{ \mathbf{r} = \lambda_1 \mathbf{r}_1 + \lambda_2 \mathbf{r}_2 + \lambda_3 \mathbf{r}_3, }[/math]
The three numbers [math]\displaystyle{ \lambda_1,\lambda_2,\lambda_3 }[/math] indicate the "barycentric" or "area" coordinates of the point [math]\displaystyle{ \mathbf{r} }[/math] with respect to the triangle. They are often denoted as [math]\displaystyle{ \alpha,\beta,\gamma }[/math] instead of [math]\displaystyle{ \lambda_1,\lambda_2,\lambda_3 }[/math]. Note that although there are three coordinates, there are only two degrees of freedom, since [math]\displaystyle{ \lambda_1+\lambda_2+\lambda_3=1 }[/math]. Thus every point is uniquely defined by any two of the barycentric coordinates.
To explain why these coordinates are signed ratios of areas, let us assume that we work in the Euclidean space [math]\displaystyle{ \mathbf{E}^{3} }[/math]. Here, consider the Cartesian coordinate system [math]\displaystyle{ Oxyz }[/math] and its associated basis, namely [math]\displaystyle{ \{\mathbf{i},\mathbf{j},\mathbf{k}\} }[/math]. Consider also the positively oriented triangle [math]\displaystyle{ ABC }[/math] lying in the [math]\displaystyle{ Oxy }[/math] plane. It is known that for any basis [math]\displaystyle{ \{\mathbf{e},\mathbf{f},\mathbf{g}\} }[/math] of [math]\displaystyle{ \mathbf{E}^{3} }[/math] and any free vector [math]\displaystyle{ \mathbf{h} }[/math] one has[9]
[math]\displaystyle{ \mathbf{h} = \frac{1}{(\mathbf{e}, \mathbf{f}, \mathbf{g})} \cdot \bigl[(\mathbf{h}, \mathbf{f}, \mathbf{g})\mathbf{e} + (\mathbf{e}, \mathbf{h}, \mathbf{g})\mathbf{f} + (\mathbf{e}, \mathbf{f}, \mathbf{h})\mathbf{g}\bigr], }[/math]
where [math]\displaystyle{ (\mathbf{e}, \mathbf{f}, \mathbf{g}) = (\mathbf{e} \times \mathbf{f}) \cdot \mathbf{g} }[/math] stands for the mixed product of these three vectors.
Take [math]\displaystyle{ \mathbf{e} = \vec{AB},\,\mathbf{f} = \vec{AC},\,\mathbf{g} = \mathbf{k},\,\mathbf{h}=\vec{AP}, }[/math] where [math]\displaystyle{ P }[/math] is an arbitrary point in the plane [math]\displaystyle{ Oxy }[/math], and remark that
[math]\displaystyle{ (\mathbf{e}, \mathbf{f}, \mathbf{h}) = \Bigl(\vec{AB} \times \vec{AC}\Bigr) \cdot \vec{AP} = \Bigl(\,\Bigl| \vec{AB} \times \vec{AC}\Bigr| \mathbf{k} \Bigr) \cdot \vec{AP} = 0. }[/math]
A subtle point regarding our choice of free vectors: [math]\displaystyle{ \mathbf{e} }[/math] is, in fact, the equipollence class of the bound vector [math]\displaystyle{ \vec{AB} }[/math].
We have obtained that
[math]\displaystyle{ \vec{AP}=m_B\cdot\vec{AB}+m_C\cdot\vec{AC} }[/math]
where [math]\displaystyle{ m_B = \frac{\Bigl(\vec{AP}, \vec{AC}, \mathbf{k}\Bigr)}{\Bigl(\vec{AB}, \vec{AC}, \mathbf{k}\Bigr)}, \quad m_C = \frac{\Bigl(\vec{AB}, \vec{AP}, \mathbf{k}\Bigr)}{\Bigl(\vec{AB}, \vec{AC}, \mathbf{k}\Bigr)}. }[/math]
Given the positive (counterclockwise) orientation of triangle [math]\displaystyle{ ABC }[/math], the denominator of both [math]\displaystyle{ m_B }[/math] and [math]\displaystyle{ m_C }[/math] is precisely the double of the area of the triangle [math]\displaystyle{ ABC }[/math]. Also,
[math]\displaystyle{ \begin{align} \Bigl(\vec{AP}, \vec{AC}, \mathbf{k}\Bigr) &= \Bigl(\vec{PC}, \vec{PA}, \mathbf{k}\Bigr), \\[2pt] \Bigl(\vec{AB}, \vec{AP}, \mathbf{k}\Bigr) &= \Bigl(\vec{PA}, \vec{PB}, \mathbf{k}\Bigr), \end{align} }[/math]
and so the numerators of [math]\displaystyle{ m_B }[/math] and [math]\displaystyle{ m_C }[/math] are the doubles of the signed areas of triangles [math]\displaystyle{ APC }[/math] and respectively [math]\displaystyle{ ABP }[/math].
Further, we deduce that
[math]\displaystyle{ \vec{OP} = (1-m_B-m_C) \cdot \vec{OA} + m_B \cdot \vec{OB} + m_C \cdot \vec{OC} }[/math]
which means that the numbers [math]\displaystyle{ 1-m_B-m_C }[/math], [math]\displaystyle{ m_B }[/math] and [math]\displaystyle{ m_C }[/math] are the barycentric coordinates of [math]\displaystyle{ P }[/math]. Similarly, the third barycentric coordinate reads as
[math]\displaystyle{ m_A = 1 - m_B - m_C = \frac{\Bigl(\vec{PB}, \vec{PC}, \mathbf{k}\Bigr)}{\Bigl(\vec{AB}, \vec{AC}, \mathbf{k}\Bigr)}. }[/math]
This [math]\displaystyle{ m }[/math]-letter notation of the barycentric coordinates comes from the fact that the point [math]\displaystyle{ P }[/math] may be interpreted as the center of mass for the masses [math]\displaystyle{ m_A }[/math], [math]\displaystyle{ m_B }[/math], [math]\displaystyle{ m_C }[/math] which are located in [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math] and [math]\displaystyle{ C }[/math].
Switching back and forth between the barycentric coordinates and other coordinate systems makes some problems much easier to solve.
Conversion between barycentric and Cartesian coordinates
Edge approach
Given a point [math]\displaystyle{ \mathbf{r} }[/math] in a triangle's plane one can obtain the barycentric coordinates [math]\displaystyle{ \lambda_1 }[/math], [math]\displaystyle{ \lambda_2 }[/math] and [math]\displaystyle{ \lambda_3 }[/math] from the Cartesian coordinates [math]\displaystyle{ (x, y) }[/math] or vice versa.
We can write the Cartesian coordinates of the point [math]\displaystyle{ \mathbf{r} }[/math] in terms of the Cartesian components of the triangle vertices [math]\displaystyle{ \mathbf{r}_1 }[/math], [math]\displaystyle{ \mathbf{r}_2 }[/math], [math]\displaystyle{ \mathbf{r}_3 }[/math] where [math]\displaystyle{ \mathbf{r}_i = (x_i, y_i) }[/math] and in terms of the barycentric coordinates of [math]\displaystyle{ \mathbf{r} }[/math] as
[math]\displaystyle{ \begin{align} x &= \lambda_1 x_1 + \lambda_2 x_2 + \lambda_3 x_3 \\[2pt] y &= \lambda_1 y_1 + \lambda_2 y_2 + \lambda_3 y_3 \end{align} }[/math]
That is, the Cartesian coordinates of any point are a weighted average of the Cartesian coordinates of the triangle's vertices, with the weights being the point's barycentric coordinates summing to unity.
To find the reverse transformation, from Cartesian coordinates to barycentric coordinates, we first substitute [math]\displaystyle{ \lambda_3 = 1 - \lambda_1 - \lambda_2 }[/math] into the above to obtain
[math]\displaystyle{ \begin{align} x &= \lambda_1 x_1 + \lambda_2 x_2 + (1 - \lambda_1 - \lambda_2) x_3 \\[2pt] y &= \lambda_1 y_1 + \lambda_2 y_2 + (1 - \lambda_1 - \lambda_2) y_3 \end{align} }[/math]
Rearranging, this is
[math]\displaystyle{ \begin{align} \lambda_1(x_1 - x_3) + \lambda_2(x_2 - x_3) + x_3 - x &= 0 \\[2pt] \lambda_1(y_1 - y_3) + \lambda_2(y_2 -\, y_3) + y_3 - \, y &= 0 \end{align} }[/math]
This linear transformation may be written more succinctly as
[math]\displaystyle{ \mathbf{T} \cdot \lambda = \mathbf{r}-\mathbf{r}_3 }[/math]
where [math]\displaystyle{ \lambda }[/math] is the vector of the first two barycentric coordinates, [math]\displaystyle{ \mathbf{r} }[/math] is the vector of Cartesian coordinates, and [math]\displaystyle{ \mathbf{T} }[/math] is a matrix given by
[math]\displaystyle{ \mathbf{T} = \left(\begin{matrix} x_1-x_3 & x_2-x_3 \\ y_1-y_3 & y_2-y_3 \end{matrix}\right) }[/math]
Now the matrix [math]\displaystyle{ \mathbf{T} }[/math] is invertible, since [math]\displaystyle{ \mathbf{r}_1-\mathbf{r}_3 }[/math] and [math]\displaystyle{ \mathbf{r}_2-\mathbf{r}_3 }[/math] are linearly independent (if this were not the case, then [math]\displaystyle{ \mathbf{r}_1 }[/math], [math]\displaystyle{ \mathbf{r}_2 }[/math], and [math]\displaystyle{ \mathbf{r}_3 }[/math] would be collinear and would not form a triangle). Thus, we can rearrange the above equation to get
[math]\displaystyle{ \left(\begin{matrix}\lambda_1 \\ \lambda_2\end{matrix}\right) = \mathbf{T}^{-1} ( \mathbf{r}-\mathbf{r}_3 ) }[/math]
Finding the barycentric coordinates has thus been reduced to finding the 2×2 inverse matrix of [math]\displaystyle{ \mathbf{T} }[/math], an easy problem.
Explicitly, the formulae for the barycentric coordinates of point [math]\displaystyle{ \mathbf{r} }[/math] in terms of its Cartesian coordinates (x, y) and in terms of the Cartesian coordinates of the triangle's vertices are:
[math]\displaystyle{ \begin{align} \lambda_1 =&\ \frac{(y_2-y_3)(x-x_3) + (x_3-x_2)(y-y_3)}{\det(\mathbf T)} \\[4pt] &= \frac{(y_2-y_3)(x-x_3) + (x_3-x_2)(y-y_3)}{(y_2-y_3)(x_1-x_3) + (x_3-x_2)(y_1-y_3)} \\[12pt] \lambda_2 =&\ \frac{(y_3-y_1)(x-x_3) + (x_1-x_3)(y-y_3)}{\det(\mathbf T)} \\[4pt] &= \frac{(y_3-y_1)(x-x_3) + (x_1-x_3)(y-y_3)}{(y_2-y_3)(x_1-x_3) + (x_3-x_2)(y_1-y_3)} \\[12pt] \lambda_3 =&\ 1 - \lambda_1 - \lambda_2 \end{align} }[/math]
Vertex approach
Another way to solve the conversion from Cartesian to barycentric coordinates is to write the relation in the matrix form [math]\displaystyle{ \mathbf{R} \boldsymbol{\lambda} = \mathbf{r} }[/math]with [math]\displaystyle{ \mathbf{R} = \left(\, \mathbf{r}_1 \,|\, \mathbf{r}_2 \,|\, \mathbf{r}_3 \right) }[/math] and [math]\displaystyle{ \boldsymbol{\lambda} = \left(\lambda_1,\lambda_2,\lambda_3\right)^\top, }[/math] i.e.[math]\displaystyle{ \begin{pmatrix} x_1 & x_2 & x_3\\ y_1 & y_2 & y_3 \end{pmatrix} \begin{pmatrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{pmatrix} = \begin{pmatrix}x\\y\end{pmatrix} }[/math]To get the unique normalized solution we need to add the condition [math]\displaystyle{ \lambda_1 + \lambda_2 + \lambda_3 = 1 }[/math]. The barycentric coordinates are thus the solution of the linear system[math]\displaystyle{ \left(\begin{matrix} 1 & 1 & 1 \\ x_1 & x_2 & x_3\\ y_1 & y_2 & y_3 \end{matrix}\right) \begin{pmatrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{pmatrix} = \left(\begin{matrix} 1\\x\\y \end{matrix}\right) }[/math]which is[math]\displaystyle{ \begin{pmatrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{pmatrix} = \frac{1}{2A} \begin{pmatrix} x_2y_3-x_3y_2 & y_2-y_3 & x_3-x_2 \\ x_3y_1-x_1y_3 & y_3-y_1 & x_1-x_3 \\ x_1y_2-x_2y_1 & y_1-y_2 & x_2-x_1 \end{pmatrix}\begin{pmatrix} 1\\x\\y \end{pmatrix} }[/math]where [math]\displaystyle{ 2A = \det(1|R) = x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2) }[/math]is twice the signed area of the triangle. The area interpretation of the barycentric coordinates can be recovered by applying Cramer's rule to this linear system.
Conversion between barycentric and trilinear coordinates
A point with trilinear coordinates x : y : z has barycentric coordinates ax : by : cz where a, b, c are the side lengths of the triangle. Conversely, a point with barycentrics [math]\displaystyle{ \lambda_1 : \lambda_2 : \lambda_3 }[/math] has trilinears [math]\displaystyle{ \lambda_1/a:\lambda_2/b:\lambda_3/c. }[/math]
Equations in barycentric coordinates
The three sides a, b, c respectively have equations[10]
[math]\displaystyle{ \lambda_1=0, \quad \lambda_2=0, \quad \lambda_3=0. }[/math]
The equation of a triangle's Euler line is[10]
[math]\displaystyle{ \begin{vmatrix} \lambda_1 & \lambda_2 & \lambda_3 \\1 & 1 & 1\\\tan A & \tan B & \tan C \end{vmatrix} =0. }[/math]
Using the previously given conversion between barycentric and trilinear coordinates, the various other equations given in Trilinear coordinates can be rewritten in terms of barycentric coordinates.
Distance between points
The displacement vector of two normalized points [math]\displaystyle{ P=(p_1,p_2,p_3) }[/math] and [math]\displaystyle{ Q=(q_1,q_2,q_3) }[/math] is[11]
[math]\displaystyle{ \overrightarrow{P Q}=(p_1-q_1,p_2-q_2,p_3-q_3). }[/math]
The distance [math]\displaystyle{ d }[/math] between [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q }[/math], or the length of the displacement vector [math]\displaystyle{ \overrightarrow{P Q}=(x,y,z), }[/math] is[10][11]
[math]\displaystyle{ \begin{align} d^2 &= |PQ|^2 \\[2pt] &= -a^2yz - b^2zx - c^2xy \\[4pt] &= \frac{1}{2} \Bigl[x^2(b^2+c^2-a^2) + y^2(c^2+a^2-b^2) + z^2(a^2+b^2-c^2)\Bigr]. \end{align} }[/math]
where a, b, c are the sidelengths of the triangle. The equivalence of the last two expressions follows from [math]\displaystyle{ x+y+z=0, }[/math] which holds because [math]\displaystyle{ \begin{align} x+y+z &= (p_1-q_1) + (p_2-q_2) + (p_3-q_3) \\[2pt] &= (p_1+p_2+p_3) - (q_1+q_2+q_3) \\[2pt] &= 1 - 1 = 0. \end{align} }[/math]
The barycentric coordinates of a point can be calculated based on distances di to the three triangle vertices by solving the equation [math]\displaystyle{ \left(\begin{matrix} -c^2 & c^2 & b^2-a^2 \\ -b^2 & c^2-a^2 & b^2 \\ 1 & 1 & 1 \end{matrix}\right)\boldsymbol{\lambda} = \left(\begin{matrix} d^2_A - d^2_B \\ d^2_A - d^2_C \\ 1 \end{matrix}\right). }[/math]
Applications

Determining location with respect to a triangle
Although barycentric coordinates are most commonly used to handle points inside a triangle, they can also be used to describe a point outside the triangle. If the point is not inside the triangle, then we can still use the formulas above to compute the barycentric coordinates. However, since the point is outside the triangle, at least one of the coordinates will violate our original assumption that [math]\displaystyle{ \lambda_{1...3}\geq 0 }[/math]. In fact, given any point in cartesian coordinates, we can use this fact to determine where this point is with respect to a triangle.
If a point lies in the interior of the triangle, all of the Barycentric coordinates lie in the open interval [math]\displaystyle{ (0,1). }[/math] If a point lies on an edge of the triangle but not at a vertex, one of the area coordinates [math]\displaystyle{ \lambda_{1...3} }[/math] (the one associated with the opposite vertex) is zero, while the other two lie in the open interval [math]\displaystyle{ (0,1). }[/math] If the point lies on a vertex, the coordinate associated with that vertex equals 1 and the others equal zero. Finally, if the point lies outside the triangle at least one coordinate is negative.
Summarizing,
- Point [math]\displaystyle{ \mathbf{r} }[/math] lies inside the triangle if and only if [math]\displaystyle{ 0 \lt \lambda_i \lt 1 \;\forall\; i \text{ in } {1,2,3} }[/math].
[math]\displaystyle{ \mathbf{r} }[/math] lies on the edge or corner of the triangle if [math]\displaystyle{ 0 \leq \lambda_i \leq 1 \;\forall\; i \text{ in } {1,2,3} }[/math] and [math]\displaystyle{ \lambda_i = 0\; \text {, for some i in } {1, 2, 3} }[/math].
- Otherwise, [math]\displaystyle{ \mathbf{r} }[/math] lies outside the triangle.
In particular, if a point lies on the far side of a line the barycentric coordinate of the point in the triangle that is not on the line will have a negative value.
Interpolation on a triangular unstructured grid
If [math]\displaystyle{ f(\mathbf{r}_1),f(\mathbf{r}_2),f(\mathbf{r}_3) }[/math] are known quantities, but the values of [math]\displaystyle{ f }[/math] inside the triangle defined by [math]\displaystyle{ \mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3 }[/math] is unknown, they can be approximated using linear interpolation. Barycentric coordinates provide a convenient way to compute this interpolation. If [math]\displaystyle{ \mathbf{r} }[/math] is a point inside the triangle with barycentric coordinates [math]\displaystyle{ \lambda_1 }[/math], [math]\displaystyle{ \lambda_2 }[/math], [math]\displaystyle{ \lambda_3 }[/math], then
[math]\displaystyle{ f(\mathbf{r}) \approx \lambda_1 f(\mathbf{r}_1) + \lambda_2 f(\mathbf{r}_2) + \lambda_3 f(\mathbf{r}_3) }[/math]
In general, given any unstructured grid or polygon mesh, this kind of technique can be used to approximate the value of [math]\displaystyle{ f }[/math] at all points, as long as the function's value is known at all vertices of the mesh. In this case, we have many triangles, each corresponding to a different part of the space. To interpolate a function [math]\displaystyle{ f }[/math] at a point [math]\displaystyle{ \mathbf{r} }[/math], first a triangle must be found that contains [math]\displaystyle{ \mathbf{r} }[/math]. To do so, [math]\displaystyle{ \mathbf{r} }[/math] is transformed into the barycentric coordinates of each triangle. If some triangle is found such that the coordinates satisfy [math]\displaystyle{ 0 \leq \lambda_i \leq 1 \;\forall\; i \text{ in } 1,2,3 }[/math], then the point lies in that triangle or on its edge (explained in the previous section). Then the value of [math]\displaystyle{ f(\mathbf{r}) }[/math] can be interpolated as described above.
These methods have many applications, such as the finite element method (FEM).
Integration over a triangle or tetrahedron
The integral of a function over the domain of the triangle can be annoying to compute in a cartesian coordinate system. One generally has to split the triangle up into two halves, and great messiness follows. Instead, it is often easier to make a change of variables to any two barycentric coordinates, e.g. [math]\displaystyle{ \lambda_1,\lambda_2 }[/math]. Under this change of variables,
[math]\displaystyle{ \int_{T} f(\mathbf{r}) \ d\mathbf{r} = 2A \int_{0}^{1} \int_{0}^{1 - \lambda_2} f(\lambda_1 \mathbf{r}_1 + \lambda_2 \mathbf{r}_2 + (1 - \lambda_1 - \lambda_2) \mathbf{r}_3) \ d\lambda_1 \ d\lambda_2 }[/math]
where [math]\displaystyle{ A }[/math] is the area of the triangle. This result follows from the fact that a rectangle in barycentric coordinates corresponds to a quadrilateral in cartesian coordinates, and the ratio of the areas of the corresponding shapes in the corresponding coordinate systems is given by [math]\displaystyle{ 2A }[/math]. Similarly, for integration over a tetrahedron, instead of breaking up the integral into two or three separate pieces, one could switch to 3D tetrahedral coordinates under the change of variables
[math]\displaystyle{ \int\int_{T} f(\mathbf{r}) \ d\mathbf{r} = 6V \int_{0}^{1} \int_{0}^{1 - \lambda_3} \int_ {0}^{1-\lambda_2-\lambda_3} f(\lambda_1\mathbf{r}_1 + \lambda_2\mathbf{r}_2 + \lambda_3\mathbf{r}_3 + (1-\lambda_1-\lambda_2-\lambda_3)\mathbf{r}_4) \ d\lambda_1 \ d\lambda_2 \ d\lambda_3 }[/math]where [math]\displaystyle{ V }[/math] is the volume of the tetrahedron.
Examples of special points
In the homogeneous barycentric coordinate system defined with respect to a triangle [math]\displaystyle{ ABC }[/math], the following statements about special points of [math]\displaystyle{ ABC }[/math] hold.
The three vertices [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], and [math]\displaystyle{ C }[/math] have coordinates[10]
[math]\displaystyle{ \begin{array}{rccccc} A = & 1 &:& 0 &:& 0 \\ B = & 0 &:& 1 &:& 0 \\ C = & 0 &:& 0 &:& 1 \end{array} }[/math]
The centroid has coordinates [math]\displaystyle{ 1:1:1. }[/math][10]
If [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math], [math]\displaystyle{ c }[/math] are the edge lengths [math]\displaystyle{ BC }[/math], [math]\displaystyle{ CA }[/math], [math]\displaystyle{ AB }[/math] respectively, [math]\displaystyle{ \alpha }[/math], [math]\displaystyle{ \beta }[/math], [math]\displaystyle{ \gamma }[/math] are the angle measures [math]\displaystyle{ \angle CAB }[/math], [math]\displaystyle{ \angle ABC }[/math], and [math]\displaystyle{ \angle BCA }[/math] respectively, and [math]\displaystyle{ s }[/math] is the semiperimeter of [math]\displaystyle{ ABC }[/math], then the following statements about special points of [math]\displaystyle{ ABC }[/math] hold in addition.
The circumcenter has coordinates[10][11][12][13]
[math]\displaystyle{ \begin{array}{rccccc} & \sin 2\alpha &:& \sin 2\beta &:& \sin 2\gamma \\[2pt] =& 1-\cos\beta\cos\gamma &:& 1-\cos\gamma\cos\alpha &:& 1-\cos\alpha\cos\beta \\[2pt] =& a^2(-a^2+b^2+c^2) &:& b^2(a^2-b^2+c^2) &:& c^2(a^2+b^2-c^2) \end{array} }[/math]
The orthocenter has coordinates[10][11]
[math]\displaystyle{ \begin{array}{rccccc} & \tan\alpha &:& \tan\beta &:& \tan\gamma \\[2pt] =& a\cos\beta\cos\gamma &:& b\cos\gamma\cos\alpha &:& c\cos\alpha\cos\beta \\[2pt] =& (a^2+b^2-c^2)(a^2-b^2+c^2) &:& (-a^2+b^2+c^2)(a^2+b^2-c^2) &:& (a^2-b^2+c^2)(-a^2+b^2+c^2) \end{array} }[/math]
The incenter has coordinates [math]\displaystyle{ a:b:c=\sin \alpha:\sin \beta:\sin \gamma. }[/math][11][14]
The excenters have coordinates[14]
[math]\displaystyle{ \begin{array}{rrcrcr} J_A = & -a &:& b &:& c \\ J_B = & a &:& -b &:& c \\ J_C = & a &:& b &:& -c \end{array} }[/math]
The nine-point center has coordinates[10][14]
[math]\displaystyle{ \begin{array}{rccccc} & a\cos(\beta-\gamma) &:& b\cos(\gamma-\alpha) &:& c\cos(\alpha-\beta) \\[4pt] =& 1+\cos\beta\cos\gamma &:& 1+\cos\gamma\cos\alpha &:& 1+\cos\alpha\cos\beta \\[4pt] =& a^2(b^2+c^2) - (b^2-c^2)^2 &:& b^2(c^2+a^2) - (c^2-a^2)^2 &:& c^2(a^2+b^2) - (a^2-b^2)^2 \end{array} }[/math]
The Gergonne point has coordinates [math]\displaystyle{ (s-b)(s-c):(s-c)(s-a):(s-a)(s-b) }[/math].
The Nagel point has coordinates [math]\displaystyle{ s-a:s-b:s-c }[/math].
The symmedian point has coordinates [math]\displaystyle{ a^2:b^2:c^2 }[/math].[13]
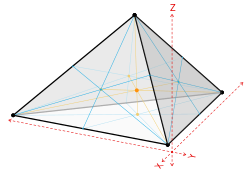
Barycentric coordinates on tetrahedra
Barycentric coordinates may be easily extended to three dimensions. The 3D simplex is a tetrahedron, a polyhedron having four triangular faces and four vertices. Once again, the four barycentric coordinates are defined so that the first vertex [math]\displaystyle{ \mathbf{r}_1 }[/math] maps to barycentric coordinates [math]\displaystyle{ \lambda = (1,0,0,0) }[/math], [math]\displaystyle{ \mathbf{r}_2 \to (0,1,0,0) }[/math], etc.
This is again a linear transformation, and we may extend the above procedure for triangles to find the barycentric coordinates of a point [math]\displaystyle{ \mathbf{r} }[/math] with respect to a tetrahedron:
[math]\displaystyle{ \left(\begin{matrix}\lambda_1 \\ \lambda_2 \\ \lambda_3\end{matrix}\right) = \mathbf{T}^{-1} ( \mathbf{r}-\mathbf{r}_4 ) }[/math]
where [math]\displaystyle{ \mathbf{T} }[/math] is now a 3×3 matrix:
[math]\displaystyle{ \mathbf{T} = \left(\begin{matrix} x_1-x_4 & x_2-x_4 & x_3-x_4\\ y_1-y_4 & y_2-y_4 & y_3-y_4\\ z_1-z_4 & z_2-z_4 & z_3-z_4 \end{matrix}\right) }[/math]
and [math]\displaystyle{ \lambda_4 = 1 - \lambda_1 - \lambda_2 - \lambda_3 }[/math]with the corresponding Cartesian coordinates:[math]\displaystyle{ \begin{align} x &= \lambda_1 x_1 + \lambda_2 x_2 + \lambda_3 x_3 + (1-\lambda_1-\lambda_2-\lambda_3)x_4 \\ y &= \lambda_1 y_1 + \,\lambda_2 y_2 + \lambda_3 y_3 + (1-\lambda_1-\lambda_2-\lambda_3)y_4 \\ z &= \lambda_1 z_1 + \,\lambda_2 z_2 + \lambda_3 z_3 + (1-\lambda_1-\lambda_2-\lambda_3)z_4 \end{align} }[/math]Once again, the problem of finding the barycentric coordinates has been reduced to inverting a 3×3 matrix.
3D barycentric coordinates may be used to decide if a point lies inside a tetrahedral volume, and to interpolate a function within a tetrahedral mesh, in an analogous manner to the 2D procedure. Tetrahedral meshes are often used in finite element analysis because the use of barycentric coordinates can greatly simplify 3D interpolation.
Generalized barycentric coordinates
Barycentric coordinates [math]\displaystyle{ (\lambda_1, \lambda_2, ..., \lambda_k) }[/math] of a point [math]\displaystyle{ p \in \mathbb{R}^n }[/math] that are defined with respect to a finite set of k points [math]\displaystyle{ x_1, x_2, ..., x_k \in \mathbb{R}^n }[/math] instead of a simplex are called generalized barycentric coordinates. For these, the equation
[math]\displaystyle{ (\lambda_1 + \lambda_2 + \cdots + \lambda_k)p = \lambda_1 x_1 + \lambda_2 x_2 + \cdots + \lambda_k x_k }[/math]
is still required to hold.[15] Usually one uses normalized coordinates, [math]\displaystyle{ \lambda_1 + \lambda_2 + \cdots + \lambda_k = 1 }[/math]. As for the case of a simplex, the points with nonnegative normalized generalized coordinates ([math]\displaystyle{ 0 \le \lambda_i \le 1 }[/math]) form the convex hull of x1, ..., xn. If there are more points than in a full simplex ([math]\displaystyle{ k \gt n + 1 }[/math]) the generalized barycentric coordinates of a point are not unique, as the defining linear system (here for n=2)[math]\displaystyle{ \left(\begin{matrix} 1 & 1 & 1 & ... \\ x_1 & x_2 & x_3 & ... \\ y_1 & y_2 & y_3 & ... \end{matrix}\right) \begin{pmatrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \\ \vdots \end{pmatrix} = \left(\begin{matrix} 1\\x\\y \end{matrix}\right) }[/math]is underdetermined. The simplest example is a quadrilateral in the plane. Various kinds of additional restrictions can be used to define unique barycentric coordinates.[16]
Abstraction
More abstractly, generalized barycentric coordinates express a convex polytope with n vertices, regardless of dimension, as the image of the standard [math]\displaystyle{ (n-1) }[/math]-simplex, which has n vertices – the map is onto: [math]\displaystyle{ \Delta^{n-1} \twoheadrightarrow P. }[/math] The map is one-to-one if and only if the polytope is a simplex, in which case the map is an isomorphism; this corresponds to a point not having unique generalized barycentric coordinates except when P is a simplex.
Dual to generalized barycentric coordinates are slack variables, which measure by how much margin a point satisfies the linear constraints, and gives an embedding [math]\displaystyle{ P \hookrightarrow (\mathbf{R}_{\geq 0})^f }[/math] into the f-orthant, where f is the number of faces (dual to the vertices). This map is one-to-one (slack variables are uniquely determined) but not onto (not all combinations can be realized).
This use of the standard [math]\displaystyle{ (n-1) }[/math]-simplex and f-orthant as standard objects that map to a polytope or that a polytope maps into should be contrasted with the use of the standard vector space [math]\displaystyle{ K^n }[/math] as the standard object for vector spaces, and the standard affine hyperplane [math]\displaystyle{ \{(x_0,\ldots,x_n) \mid \sum x_i = 1\} \subset K^{n+1} }[/math] as the standard object for affine spaces, where in each case choosing a linear basis or affine basis provides an isomorphism, allowing all vector spaces and affine spaces to be thought of in terms of these standard spaces, rather than an onto or one-to-one map (not every polytope is a simplex). Further, the n-orthant is the standard object that maps to cones.
Applications
Generalized barycentric coordinates have applications in computer graphics and more specifically in geometric modelling.[17] Often, a three-dimensional model can be approximated by a polyhedron such that the generalized barycentric coordinates with respect to that polyhedron have a geometric meaning. In this way, the processing of the model can be simplified by using these meaningful coordinates. Barycentric coordinates are also used in geophysics.[18]
See also
References
- ↑ Möbius, August Ferdinand (1827). Der barycentrische Calcul. Leipzig: J.A. Barth.
Reprinted in Möbius, August Ferdinand (1885). "Der barycentrische Calcul". in Baltzer, Richard. August Ferdinand Möbius Gesammelte Werke. 1. Leipzig: S. Hirzel. pp. 1–388. https://archive.org/details/gesammeltewerkeh01mbuoft/page/n24/. - ↑ Max Koecher, Aloys Krieg: Ebene Geometrie. Springer-Verlag, Berlin 2007, ISBN:978-3-540-49328-0, S. 76.
- ↑ Hille, Einar. "Analytic Function Theory, Volume I", Second edition, fifth printing. Chelsea Publishing Company, New York, 1982, ISBN:0-8284-0269-8, page 33, footnote 1
- ↑ Josef Hoschek, Dieter Lasser: Grundlagen der geometrischen Datenverarbeitung. Teubner-Verlag, 1989, ISBN:3-519-02962-6, S. 243.
- ↑ Gerald Farin: Curves and Surfaces for Computer Aided Geometric Design. Academic Press, 1990, ISBN:0-12-249051-7, S. 20.
- ↑ Reventós Tarrida, Agustí. "Affine Maps, Euclidean Motions and Quadrics". Springer, 2011, ISBN:978-0-85729-709-9, page 11
- ↑ Deaux, Roland. "Introduction to The Geometry of Complex Numbers". Dover Publications, Inc., Mineola, 2008, ISBN:978-0-486-46629-3, page 61
- ↑ 8.0 8.1 Berger, Marcel (1987), Geometry I, Berlin: Springer, ISBN 3-540-11658-3
- ↑ Danby, J.M.A. "Fundamentals of Celestial Mechanics", Second edition, revised & enlarged, fifth printing. Willmann-Bell, Inc., Richmond, 2003, ISBN:0-943396-20-4, page 26, problem 11
- ↑ 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 Scott, J. A. "Some examples of the use of areal coordinates in triangle geometry", Mathematical Gazette 83, November 1999, 472–477.
- ↑ 11.0 11.1 11.2 11.3 11.4 Schindler, Max; Chen, Evan (July 13, 2012). "Barycentric Coordinates in Olympiad Geometry". https://www.mit.edu/~evanchen/handouts/bary/bary-full.pdf.
- ↑ Clark Kimberling's Encyclopedia of Triangles "Encyclopedia of Triangle Centers". http://faculty.evansville.edu/ck6/encyclopedia/ETC.html.
- ↑ 13.0 13.1 Wolfram page on barycentric coordinates
- ↑ 14.0 14.1 14.2 Dasari Naga, Vijay Krishna, "On the Feuerbach triangle", Forum Geometricorum 17 (2017), 289–300: p. 289. http://forumgeom.fau.edu/FG2017volume17/FG201731.pdf
- ↑ Meyer, Mark; Barr, Alan; Lee, Haeyoung; Desbrun, Mathieu (6 April 2012). "Generalized Barycentric Coordinates on Irregular Polygons". Journal of Graphics Tools 7: 13–22. doi:10.1080/10867651.2002.10487551. http://www.geometry.caltech.edu/pubs/MHBD02.pdf.
- ↑ Floater, Michael S. (2015). "Generalized barycentric coordinates and applications *" (in en). Acta Numerica 24: 161–214. doi:10.1017/S0962492914000129. ISSN 0962-4929. https://www.mn.uio.no/math/english/people/aca/michaelf/papers/gbc.pdf.
- ↑ Floater, Michael S. (2003). "Mean value coordinates" (in en). Computer Aided Geometric Design 20 (1): 19–27. doi:10.1016/S0167-8396(03)00002-5. https://linkinghub.elsevier.com/retrieve/pii/S0167839603000025.
- ↑ ONUFRIEV, VG; DENISIK, SA; FERRONSKY, VI, BARICENTRIC MODELS IN ISOTOPE STUDIES OF NATURAL-WATERS. NUCLEAR GEOPHYSICS, 4, 111-117 (1990)
- Scott, J. A. Some examples of the use of areal coordinates in triangle geometry, Mathematical Gazette 83, November 1999, 472–477.
- Schindler, Max; Chen, Evan (July 13, 2012). Barycentric Coordinates in Olympiad Geometry (PDF). Retrieved 14 January 2016.
- Clark Kimberling's Encyclopedia of Triangles Encyclopedia of Triangle Centers. Archived from the original on 2012-04-19. Retrieved 2012-06-02.
- Bradley, Christopher J. (2007). The Algebra of Geometry: Cartesian, Areal and Projective Co-ordinates. Bath: Highperception. ISBN 978-1-906338-00-8.
- Coxeter, H.S.M. (1969). Introduction to geometry (2nd ed.). John Wiley and Sons. pp. 216–221. ISBN 978-0-471-50458-0. https://archive.org/details/introductiontoge00coxe.
- Barycentric Calculus In Euclidean And Hyperbolic Geometry: A Comparative Introduction, Abraham Ungar, World Scientific, 2010
- Hyperbolic Barycentric Coordinates, Abraham A. Ungar, The Australian Journal of Mathematical Analysis and Applications, Vol.6, No.1, Article 18, pp. 1–35, 2009
- Weisstein, Eric W.. "Areal Coordinates". http://mathworld.wolfram.com/ArealCoordinates.html.
- Weisstein, Eric W.. "Barycentric Coordinates". http://mathworld.wolfram.com/BarycentricCoordinates.html.
- Barycentric coordinates computation in homogeneous coordinates, Vaclav Skala, Computers and Graphics, Vol.32, No.1, pp. 120–127, 2008
External links
- Law of the lever
- The uses of homogeneous barycentric coordinates in plane euclidean geometry
- Barycentric Coordinates – a collection of scientific papers about (generalized) barycentric coordinates
- Barycentric coordinates: A Curious Application (solving the "three glasses" problem) at cut-the-knot
- Accurate point in triangle test
- Barycentric Coordinates in Olympiad Geometry by Evan Chen and Max Schindler
- Barycenter command and TriangleCurve command at Geogebra.
 |