Feigenbaum constants

From HandWiki
Revision as of 17:32, 6 February 2024 by Wincert (talk | contribs) (linkage)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Mathematical constants related to chaotic behavior
Feigenbaum constant δ expresses the limit of the ratio of distances between consecutive bifurcation diagram on Li/Li + 1

In mathematics, specifically bifurcation theory, the Feigenbaum constants /ˈfaɪɡənˌbaʊm/[1] are two mathematical constants which both express ratios in a bifurcation diagram for a non-linear map. They are named after the physicist Mitchell J. Feigenbaum.

History

Feigenbaum originally related the first constant to the period-doubling bifurcations in the logistic map, but also showed it to hold for all one-dimensional maps with a single quadratic maximum. As a consequence of this generality, every chaotic system that corresponds to this description will bifurcate at the same rate. Feigenbaum made this discovery in 1975,[2][3] and he officially published it in 1978.[4]

The first constant

The first Feigenbaum constant δ is the limiting ratio of each bifurcation interval to the next between every period doubling, of a one-parameter map

[math]\displaystyle{ x_{i+1} = f(x_i), }[/math]

where f(x) is a function parameterized by the bifurcation parameter a.

It is given by the limit[5]

[math]\displaystyle{ \delta = \lim_{n \to \infty} \frac{a_{n-1} - a_{n-2}}{a_n - a_{n-1}} = 4.669\,201\,609\,\ldots, }[/math]

where an are discrete values of a at the nth period doubling.

Names

  • Feigenbaum constant
  • Feigenbaum bifurcation velocity
  • delta

Value

  • 30 decimal places : δ = 4.669201609102990671853203820466…
  • (sequence A006890 in the OEIS)
  • A simple rational approximation is: 621/133, which is correct to 5 significant values (when rounding). For more precision use 1228/263, which is correct to 7 significant values.
  • Is approximately equal to 10(1/π − 1), with an error of 0.0047%

Illustration

Non-linear maps

To see how this number arises, consider the real one-parameter map

[math]\displaystyle{ f(x)=a-x^2. }[/math]

Here a is the bifurcation parameter, x is the variable. The values of a for which the period doubles (e.g. the largest value for a with no period-2 orbit, or the largest a with no period-4 orbit), are a1, a2 etc. These are tabulated below:[6]

n Period Bifurcation parameter (an) Ratio an−1 − an−2/an − an−1
1 2 0.75 —
2 4 1.25 —
3 8 1.3680989 4.2337
4 16 1.3940462 4.5515
5 32 1.3996312 4.6458
6 64 1.4008286 4.6639
7 128 1.4010853 4.6682
8 256 1.4011402 4.6689

The ratio in the last column converges to the first Feigenbaum constant. The same number arises for the logistic map

[math]\displaystyle{ f(x) = a x (1 - x) }[/math]

with real parameter a and variable x. Tabulating the bifurcation values again:[7]

n Period Bifurcation parameter (an) Ratio an−1 − an−2/an − an−1
1 2 3 —
2 4 3.4494897 —
3 8 3.5440903 4.7514
4 16 3.5644073 4.6562
5 32 3.5687594 4.6683
6 64 3.5696916 4.6686
7 128 3.5698913 4.6680
8 256 3.5699340 4.6768

Fractals

Self-similarity in the Mandelbrot set shown by zooming in on a round feature while panning in the negative-x direction. The display center pans from (−1, 0) to (−1.31, 0) while the view magnifies from 0.5 × 0.5 to 0.12 × 0.12 to approximate the Feigenbaum ratio.

In the case of the Mandelbrot set for complex quadratic polynomial

[math]\displaystyle{ f(z) = z^2 + c }[/math]

the Feigenbaum constant is the limiting ratio between the diameters of successive circles on the real axis in the complex plane (see animation on the right).

n Period = 2n Bifurcation parameter (cn) Ratio [math]\displaystyle{ = \dfrac{c_{n-1}-c_{n-2}}{c_n-c_{n-1}} }[/math]
1 2 −0.75 —
2 4 −1.25 —
3 8 −1.3680989 4.2337
4 16 −1.3940462 4.5515
5 32 −1.3996312 4.6459
6 64 −1.4008287 4.6639
7 128 −1.4010853 4.6668
8 256 −1.4011402 4.6740
9 512 −1.401151982029 4.6596
10 1024 −1.401154502237 4.6750
∞ −1.4011551890...

Bifurcation parameter is a root point of period-2n component. This series converges to the Feigenbaum point c = −1.401155...... The ratio in the last column converges to the first Feigenbaum constant.

Julia set for the Feigenbaum point

Other maps also reproduce this ratio; in this sense the Feigenbaum constant in bifurcation theory is analogous to π in geometry and e in calculus.

The second constant

The second Feigenbaum constant or Feigenbaum's alpha constant (sequence A006891 in the OEIS),

[math]\displaystyle{ \alpha = 2.502\,907\,875\,095\,892\,822\,283\,902\,873\,218..., }[/math]

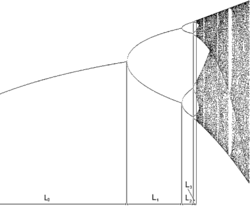
is the ratio between the width of a tine and the width of one of its two subtines (except the tine closest to the fold). A negative sign is applied to α when the ratio between the lower subtine and the width of the tine is measured.[8]

These numbers apply to a large class of dynamical systems (for example, dripping faucets to population growth).[8]

A simple rational approximation is 13/11 × 17/11 × 37/27 = 8177/3267.

Other values

The period-3 window in the logistic map also has a period-doubling route to chaos, and it has its own two Feigenbaum constants. [math]\displaystyle{ \delta = 55.26, \alpha = 9.277 }[/math] (Appendix F.2[9]).

Properties

Both numbers are believed to be transcendental, although they have not been proven to be so.[10] In fact, there is no known proof that either constant is even irrational.

The first proof of the universality of the Feigenbaum constants was carried out by Oscar Lanford—with computer-assistance—in 1982[11] (with a small correction by Jean-Pierre Eckmann and Peter Wittwer of the University of Geneva in 1987[12]). Over the years, non-numerical methods were discovered for different parts of the proof, aiding Mikhail Lyubich in producing the first complete non-numerical proof.[13]

See also


Notes

  1. ↑ (in en) The Feigenbaum Constant (4.669) – Numberphile, https://www.youtube.com/watch?v=ETrYE4MdoLQ, retrieved 2023-02-07 
  2. ↑ Feigenbaum, M. J. (1976). "Universality in complex discrete dynamics". Los Alamos Theoretical Division Annual Report 1975–1976. http://chaosbook.org/extras/mjf/LA-6816-PR.pdf. 
  3. ↑ Alligood, K. T.; Sauer, T. D.; Yorke, J. A. (1996). Chaos: An Introduction to Dynamical Systems. Springer. ISBN 0-387-94677-2. 
  4. ↑ Feigenbaum, Mitchell J. (1978). "Quantitative universality for a class of nonlinear transformations". Journal of Statistical Physics 19 (1): 25–52. doi:10.1007/BF01020332. Bibcode: 1978JSP....19...25F. 
  5. ↑ Jordan, D. W.; Smith, P. (2007). Non-Linear Ordinary Differential Equations: Introduction for Scientists and Engineers (4th ed.). Oxford University Press. ISBN 978-0-19-920825-8. 
  6. ↑ Alligood, p. 503.
  7. ↑ Alligood, p. 504.
  8. ↑ 8.0 8.1 Strogatz, Steven H. (1994). Nonlinear Dynamics and Chaos. Studies in Nonlinearity. Perseus Books. ISBN 978-0-7382-0453-6. 
  9. ↑ Hilborn, Robert C. (2000). Chaos and nonlinear dynamics: an introduction for scientists and engineers (2nd ed.). Oxford: Oxford University Press. ISBN 0-19-850723-2. OCLC 44737300. 
  10. ↑ Briggs, Keith (1997). Feigenbaum scaling in discrete dynamical systems (PDF) (PhD thesis). University of Melbourne.
  11. ↑ Lanford III, Oscar (1982). "A computer-assisted proof of the Feigenbaum conjectures". Bull. Amer. Math. Soc. 6 (3): 427–434. doi:10.1090/S0273-0979-1982-15008-X. 
  12. ↑ Eckmann, J. P.; Wittwer, P. (1987). "A complete proof of the Feigenbaum conjectures". Journal of Statistical Physics 46 (3–4): 455. doi:10.1007/BF01013368. Bibcode: 1987JSP....46..455E. 
  13. ↑ Lyubich, Mikhail (1999). "Feigenbaum-Coullet-Tresser universality and Milnor's Hairiness Conjecture". Annals of Mathematics 149 (2): 319–420. doi:10.2307/120968. Bibcode: 1999math......3201L. 

References

External links

OEIS sequence A006891 (Decimal expansion of Feigenbaum reduction parameter)
OEIS sequence A195102 (Decimal expansion of the parameter for the biquadratic solution of the Feigenbaum-Cvitanovic equation)



Retrieved from "https://handwiki.org/wiki/index.php?title=Feigenbaum_constants&oldid=3369378"