Mathieu group M24
| Algebraic structure → Group theory Group theory |
|---|
 |
In the area of modern algebra known as group theory, the Mathieu group M24 is a sporadic simple group of order
- 210 · 33 · 5 · 7 · 11 · 23 = 244823040
- ≈ 2×108.
History and properties
M24 is one of the 26 sporadic groups and was introduced by Mathieu (1861, 1873). It is a 5-transitive permutation group on 24 objects. The Schur multiplier and the outer automorphism group are both trivial.
The Mathieu groups can be constructed in various ways. Initially, Mathieu and others constructed them as permutation groups. It was difficult to see that M24 actually existed, that its generators did not just generate the alternating group A24. The matter was clarified when Ernst Witt constructed M24 as the automorphism (symmetry) group of an S(5,8,24) Steiner system W24 (the Witt design). M24 is the group of permutations that map every block in this design to some other block. The subgroups M23 and M22 then are easily defined to be the stabilizers of a single point and a pair of points respectively.
Construction as a permutation group
M24 is the subgroup of S24 that is generated by the three permutations:[1]
- [math]\displaystyle{ (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23) }[/math]
- [math]\displaystyle{ (3,17,10,7,9)(4,13,14,19,5)(8,18,11,12,23)(15,20,22,21,16) }[/math] and
- [math]\displaystyle{ (1,24)(2,23)(3,12)(4,16)(5,18)(6,10)(7,20)(8,14)(9,21)(11,17)(13,22)(15,19) }[/math].
M24 can also be generated by two permutations:[2]
- [math]\displaystyle{ (1,16,8,23,13,14,5)(2,7,11,19,20,24,12)(3,4,17,9,22,21,15) }[/math] and
- [math]\displaystyle{ (1,24)(2,21)(3,10)(4,22)(5,9)(6,23)(7,8)(11,18)(12,20)(13,14)(15,19)(16,17). }[/math]
M24 from PSL(3,4)
M24 can be built starting from PSL(3,4), the projective special linear group of 3-dimensional space over the finite field with 4 elements (Dixon Mortimer). This group, sometimes called M21, acts on the projective plane over the field F4, an S(2,5,21) system called W21. Its 21 blocks are called lines. Any 2 lines intersect at one point.
M21 has 168 simple subgroups of order 360 and 360 simple subgroups of order 168. In the larger projective general linear group PGL(3,4) both sets of subgroups form single conjugacy classes, but in M21 both sets split into 3 conjugacy classes. The subgroups respectively have orbits of 6, called hyperovals, and orbits of 7, called Fano subplanes. These sets allow creation of new blocks for larger Steiner systems. M21 is normal in PGL(3,4), of index 3. PGL(3,4) has an outer automorphism induced by transposing conjugate elements in F4 (the field automorphism). PGL(3,4) can therefore be extended to the group PΓL(3,4) of projective semilinear transformations, which is a split extension of M21 by the symmetric group S3. PΓL(3,4) has an embedding as a maximal subgroup of M24.(Griess 1998)
A hyperoval has no 3 points that are collinear. A Fano subplane likewise satisfies suitable uniqueness conditions.
To W21 append 3 new points and let the automorphisms in PΓL(3,4) but not in M21 permute these new points. An S(3,6,22) system W22 is formed by appending just one new point to each of the 21 lines and new blocks are 56 hyperovals conjugate under M21.
An S(5,8,24) system would have 759 blocks, or octads. Append all 3 new points to each line of W21, a different new point to the Fano subplanes in each of the sets of 120, and append appropriate pairs of new points to all the hyperovals. That accounts for all but 210 of the octads. Those remaining octads are subsets of W21 and are symmetric differences of pairs of lines. There are many possible ways to expand the group PΓL(3,4) to M24.
Automorphism group of the Golay code
The group M24 also is the permutation automorphism group of the binary Golay code W, i.e., the group of permutations of coordinates mapping W to itself. Codewords correspond in a natural way to subsets of a set of 24 objects. (In coding theory the term "binary Golay code" often refers to a shorter related length 23 code, and the length 24 code used here is called the "extended binary Golay code".) Those subsets corresponding to codewords with 8 or 12 coordinates equal to 1 are called octads or dodecads respectively. The octads are the blocks of an S(5,8,24) Steiner system and the binary Golay code is the vector space over field F2 spanned by the octads of the Steiner system.
The simple subgroups M23, M22, M12, and M11 can be defined as subgroups of M24, stabilizers respectively of a single coordinate, an ordered pair of coordinates, a dodecad, and a dodecad together with a single coordinate.
There is a natural connection between the Mathieu groups and the larger Conway groups, because the binary Golay code and the Leech lattice both lie in spaces of dimension 24. The Conway groups in turn are found in the Monster group. Robert Griess refers to the 20 sporadic groups found in the Monster as the Happy Family, and to the Mathieu groups as the first generation.
Polyhedral symmetries
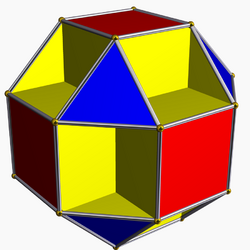
M24 can be constructed starting from the symmetries of the Klein quartic (the symmetries of a tessellation of the genus three surface), which is PSL(2,7), which can be augmented by an additional permutation. This permutation can be described by starting with the tiling of the Klein quartic by 56 triangles (with 24 vertices – the 24 points on which the group acts), then forming squares of out some of the 2 triangles, and octagons out of 6 triangles, with the added permutation being "interchange the two endpoints of those edges of the original triangular tiling which bisect the squares and octagons".[2] This can be visualized by coloring the triangles – the corresponding tiling is topologically but not geometrically the t0,1{4, 3, 3} tiling, and can be (polyhedrally) immersed in Euclidean 3-space as the small cubicuboctahedron (which also has 24 vertices).[2]
Applications
The theory of umbral moonshine is a partly conjectural relationship between K3 surfaces and M24.
The Conway group Co1, the Fischer group Fi24, and the Janko group J4 each have maximal subgroups that are an extension of the Mathieu group M24 by a group 211. (These extensions are not all the same.)[citation needed]
Representations
(Frobenius 1904) calculated the complex character table of M24.
The Mathieu group M24 has a 5-fold transitive permutation representation on 24 points. The corresponding linear representation over the complex numbers is the sum of the trivial representation and a 23-dimensional irreducible representation.[citation needed]
M24 has two rank 3 permutation representations: one on the 276 = 1+44+231 pairs of points (or duads) with stabilizer M22.2, and one on the 1288 = 1+495+792 duads, with stabilizer M12.2.[citation needed]
The quotient of the 24-dimensional linear representation of the permutation representation by its 1-dimensional fixed subspace gives a 23-dimensional representation, which is irreducible over any field of characteristic not 2 or 3, and gives the smallest faithful representation over such fields.[citation needed]
Reducing the 24-dimensional representation mod 2 gives an action on F242. This has invariant subspaces of dimension 1, 12 (the Golay code), and 23. The subquotients give two irreducible representations of dimension 11 over the field with 2 elements.[citation needed]
Maximal subgroups
(Choi 1972b) found the 9 conjugacy classes of maximal subgroups of M24. (Curtis 1977) gave a short proof of the result, describing the 9 classes in terms of combinatorial data on the 24 points: the subgroups fix a point, duad, octad, duum, sextet, triad, trio, projective line, or octern, as described below. (Todd 1966) gave the character tables of M24 (originally calculated by (Frobenius 1904)) and the 8 maximal subgroups that were known at the time.
M24 contains non-abelian simple subgroups of 13 isomorphism types: five classes of A5, four classes of PSL(3,2), two classes of A6, two classes of PSL(2,11), one class each of A7, PSL(2,23), M11, PSL(3,4), A8, M12, M22, M23, and M24.[citation needed] A6 is also noted below as a subquotient in the sextet subgroup.
The Mathieu group acts on the 2048 = 1+759+1288 points of the Golay code modulo the fixed space with 3 orbits, and on the 4096 = 1+24+276+2024+1771 points of the cocode with 5 orbits, and the subgroups fixing a non-trivial point of the code or cocode give 6 of the 9 classes of maximal subgroups.
The 9 classes of maximal subgroups are as follows:
Point subgroup
The subgroup fixing a point is M23, order 10200960.
Duad subgroup
A duad is a pair of points. The subgroup fixing a duad is M22:2, order 887040, with orbits of 2 and 22.
Octad subgroup
The subgroup fixing one of the 759 (= 3·11·23) octads of the Golay code or Steiner system is the octad group 24:A8, order 322560, with orbits of size 8 and 16. The linear group GL(4,2) has an exceptional isomorphism to the alternating group A8. The pointwise stabilizer O of an octad is an abelian group of order 16, exponent 2, each of whose involutions moves all 16 points outside the octad. The stabilizer of the octad is a split extension of O by A8. (Thompson 1983)
Duum subgroup
A duum is a pair of complementary dodecads (12 point sets) in the Golay code. The subgroup fixing a duad is M12:2, order 190080, transitive and imprimitive. This subgroup was discovered by Frobenius. The subgroup M12 acts differently on 2 sets of 12, reflecting the outer automorphism of M12.
Sextet subgroup
26:(3.S6), order 138240: sextet group
Consider a tetrad, any set of 4 points in the Steiner system W24. An octad is determined by choice of a fifth point from the remaining 20. There are 5 octads possible. Hence any tetrad determines a partition into 6 tetrads, called a sextet, whose stabilizer in M24 is called a sextet group.
The total number of tetrads is 24*23*22*21/4! = 23*22*21. Dividing that by 6 gives the number of sextets, 23*11*7 = 1771. Furthermore, a sextet group is a subgroup of a wreath product of order 6!*(4!)6, whose only prime divisors are 2, 3, and 5.[citation needed] Now we know the prime divisors of |M24|. Further analysis would determine the order of the sextet group and hence |M24|.
It is convenient to arrange the 24 points into a 6-by-4 array:
Moreover, it is convenient to use the elements of the field F4 to number the rows: 0, 1, u, u2.
The sextet group has a normal abelian subgroup H of order 64, isomorphic to the hexacode, a vector space of length 6 and dimension 3 over F4. A non-zero element in H does double transpositions within 4 or 6 of the columns. Its action can be thought of as addition of vector co-ordinates to row numbers.
The sextet group is a split extension of H by a group 3.S6 (a stem extension).[citation needed] Here is an instance within the Mathieu groups where a simple group (A6) is a subquotient, not a subgroup. 3.S6 is the normalizer in M24 of the subgroup generated by r=(BCD)(FGH)(JKL)(NOP)(RST)(VWX), which can be thought of as a multiplication of row numbers by u2. The subgroup 3.A6 is the centralizer of ⟨r⟩. Generators of 3.A6 are:
- (AEI)(BFJ)(CGK)(DHL)(RTS)(VWX) (rotating first 3 columns)
- (AQ)(BS)(CT)(DR)(EU)(FX)(GV)(HW)
- (AUEIQ)(BXGKT)(CVHLR)(DWFJS) (product of preceding two)
- (FGH)(JLK)(MQU)(NRV)(OSW)(PTX) (rotating last 3 columns).
An odd permutation of columns, say (CD)(GH)(KL)(OP)(QU)(RV)(SX)(TW), then generates 3.S6.
The group 3.A6 is isomorphic to a subgroup of SL(3,4) whose image in PSL(3,4) has been noted[by whom?] above as the hyperoval group.
The applet Moggie has a function that displays sextets in color.
Triad subgroup
A triad is a set of 3 points. The subgroup fixing a triad is PSL(3,4):S3, order 120960, with orbits of size 3 and 21.
Trio subgroup
A trio is a set of 3 disjoint octads of the Golay code. The subgroup fixing a trio is the trio group 26:(PSL(2,7) x S3), order 64512, transitive and imprimitive.
Projective line subgroup
The subgroup fixing a projective line structure on the 24 points is PSL(2,23), order 6072, whose action is doubly transitive. This subgroup was observed by Mathieu.
Octern subgroup
An octern is a certain partition of the 24 points into 8 blocks of 3. The subgroup fixing an octern is the octern group isomorphic to PSL(2,7), of order 168, simple, transitive and imprimitive. It was the last maximal subgroup of M24 to be found.
Conjugacy classes
There are 26 conjugacy classes. The cycle shapes are all balanced in the sense that they remain invariant under changing length k cycles to length N/k cycles for some integer N depending on the conjugacy class.
| Order | No. elements | Cycle structure | |
|---|---|---|---|
| 1 = 1 | 1 | 124 | |
| 2 = 2 | 11385 = 32 · 5 · 11 · 23 | 1828 | |
| 31878 = 2 · 32 · 7 · 11 · 23 | 212 | ||
| 3 = 3 | 226688 = 27 · 7 · 11 · 23 | 1636 | |
| 485760 = 27 · 3 · 5 · 11 · 23 | 38 | ||
| 4 = 22 | 637560 = 23 · 32 · 5 · 7 · 11 · 23 | 2444 | |
| 1912680 = 23 · 33 · 5 · 7 · 11 · 23 | 142244 | ||
| 2550240 = 25 · 32 · 5 · 7 · 11 · 23 | 46 | ||
| 5 = 5 | 4080384 = 28 · 33 · 7 · 11 · 23 | 1454 | |
| 6 = 2 · 3 | 10200960 = 27 · 32 · 5 · 7 · 11 · 23 | 12223262 | |
| 10200960 = 27 · 32 · 5 · 7 · 11 · 23 | 64 | ||
| 7 = 7 | 5829120 = 29 · 32 · 5 · 11 · 23 | 1373 | power equivalent |
| 5829120 = 29 · 32 · 5 · 11 · 23 | 1373 | ||
| 8 = 23 | 15301440 = 26 · 33 · 5 · 7 · 11 · 23 | 122·4·82 | |
| 10 = 2 · 5 | 12241152 = 28 · 33 · 7 · 11 · 23 | 22102 | |
| 11 = 11 | 22256640 = 210 · 33 · 5 · 7 · 23 | 12112 | |
| 12 = 22 · 3 | 20401920 = 28 · 32 · 5 · 7 · 11 · 23 | 2 ·4·6·12 | |
| 20401920 = 28 · 32 · 5 · 7 · 11 · 23 | 122 | ||
| 14 = 2 · 7 | 17487360 = 29 · 33 · 5 · 11 · 23 | 1·2·7·14 | power equivalent |
| 17487360 = 29 · 33 · 5 · 11 · 23 | 1·2·7·14 | ||
| 15 = 3 · 5 | 16321536 = 210 · 32 · 7 · 11 · 23 | 1·3·5·15 | power equivalent |
| 16321536 = 210 · 32 · 7 · 11 · 23 | 1·3·5·15 | ||
| 21 = 3 · 7 | 11658240 = 210 · 32 · 5 · 11 · 23 | 3·21 | power equivalent |
| 11658240 = 210 · 32 · 5 · 11 · 23 | 3·21 | ||
| 23 = 23 | 10644480 = 210 · 33 · 5 · 7 · 11 | 1·23 | power equivalent |
| 10644480 = 210 · 33 · 5 · 7 · 11 | 1·23 |
References
- Cameron, Peter J. (1999), Permutation Groups, London Mathematical Society Student Texts, 45, Cambridge University Press, ISBN 978-0-521-65378-7, https://archive.org/details/permutationgroup0000came
- Carmichael, Robert D. (1956), "Introduction to the theory of groups of finite order", Nature (New York: Dover Publications) 78 (2028): 442–443, doi:10.1038/078442a0, ISBN 978-0-486-60300-1, Bibcode: 1908Natur..78..442G, https://books.google.com/books?id=McMgAAAAMAAJ
- Choi, C. (May 1972a), "On Subgroups of M24. I: Stabilizers of Subsets", Transactions of the American Mathematical Society 167: 1–27, doi:10.2307/1996123
- Choi, C. (May 1972b). "On Subgroups of M24. II: the Maximal Subgroups of M24". Transactions of the American Mathematical Society 167: 29–47. doi:10.2307/1996124.
- Conway, John Horton (1971), "Three lectures on exceptional groups", in Powell, M. B.; Higman, Graham, Finite simple groups, Proceedings of an Instructional Conference organized by the London Mathematical Society (a NATO Advanced Study Institute), Oxford, September 1969., Boston, MA: Academic Press, pp. 215–247, ISBN 978-0-12-563850-0, https://books.google.com/books?id=TPPkAAAAIAAJ Reprinted in (Conway Sloane)
- Conway, John Horton; Parker, Richard A.; Norton, Simon P.; Curtis, R. T.; Wilson, Robert A. (1985), Atlas of finite groups, Oxford University Press, ISBN 978-0-19-853199-9, https://books.google.com/books?id=38fEMl2-Fp8C
- Conway, John Horton; Sloane, Neil J. A. (1999), "Sphere Packings, Lattices and Groups", Zeitschrift für Kristallographie, Grundlehren der Mathematischen Wissenschaften (Berlin, New York: Springer-Verlag) 290 (3–4): 286, doi:10.1524/zkri.1990.191.3-4.286, ISBN 978-0-387-98585-5, Bibcode: 1990ZK....191..286F, https://books.google.com/books?id=upYwZ6cQumoC
- Curtis, Robert T. (1976), "A new combinatorial approach to M24", Mathematical Proceedings of the Cambridge Philosophical Society 79 (1): 25–42, doi:10.1017/S0305004100052075, ISSN 0305-0041, Bibcode: 1976MPCPS..79...25C
- Curtis, Robert T. (1977), "The maximal subgroups of M24", Mathematical Proceedings of the Cambridge Philosophical Society 81 (2): 185–192, doi:10.1017/S0305004100053251, ISSN 0305-0041, Bibcode: 1977MPCPS..81..185C
- Curtis, Robert T. (2007), Symmetric Generation of groups, Encyclopedia of Mathematics, Cambridge, UK: Cambridge University Press, ISBN 978-0-521-85721-5, https://archive.org/details/symmetricgenerat0000curt
- Cuypers, Hans, The Mathieu groups and their geometries, http://www.win.tue.nl/~hansc/mathieu.pdf
- Dixon, John D.; Mortimer, Brian (1996), Permutation groups, Graduate Texts in Mathematics, 163, Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4612-0731-3, ISBN 978-0-387-94599-6, https://archive.org/details/permutationgroup0000dixo
- Frobenius, Ferdinand Georg (1904), "Über die Charaktere der mehrfach transitiven Gruppen" (in German), Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften (Königliche Akademie der Wissenschaften, Berlin) 16: 558–571, Reprinted in volume III of his collected works.
- Griess, Robert L. Jr. (1998), Twelve sporadic groups, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-62778-4
- Mathieu, Émile (1861), "Mémoire sur l'étude des fonctions de plusieurs quantités, sur la manière de les former et sur les substitutions qui les laissent invariables", Journal de Mathématiques Pures et Appliquées 6: 241–323, http://gallica.bnf.fr/ark:/12148/bpt6k16405f/f249
- Miller, G. A. (1898), "On the supposed five-fold transitive function of 24 elements and 19!/48 values", Messenger of Mathematics 27: 187–190, https://books.google.com/books?id=LMAKAAAAIAAJ&pg=PA187
- Miller, G. A. (1900), "Sur plusieurs groupes simples", Bulletin de la Société Mathématique de France 28: 266–267, doi:10.24033/bsmf.635, http://www.numdam.org/item?id=BSMF_1900__28__266_0
- Ronan, Mark (2006), Symmetry and the Monster, Oxford, ISBN 978-0-19-280722-9 (an introduction for the lay reader, describing the Mathieu groups in a historical context)
- Thompson, Thomas M. (1983), From error-correcting codes through sphere packings to simple groups, Carus Mathematical Monographs, 21, Mathematical Association of America, ISBN 978-0-88385-023-7, https://books.google.com/books?id=ggqxuG31B3cC
- Todd, J. A. (1966), "A representation of the Mathieu group M24 as a collineation group", Annali di Matematica Pura ed Applicata, Series 4 71: 199–238, doi:10.1007/BF02413742, ISSN 0003-4622
- Witt, Ernst (1938a), "über Steinersche Systeme", Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 12: 265–275, doi:10.1007/BF02948948, ISSN 0025-5858
- Witt, Ernst (1938b), "Die 5-fach transitiven Gruppen von Mathieu", Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 12: 256–264, doi:10.1007/BF02948947
External links
- MathWorld: Mathieu Groups
- Atlas of Finite Group Representations: M24
- Richter, David A., How to Make the Mathieu Group M24, http://homepages.wmich.edu/~drichter/mathieu.htm, retrieved 2010-04-15
 |

