Biology:Galton–Watson process
The Galton–Watson process is a branching stochastic process arising from Francis Galton's statistical investigation of the extinction of family names. The process models family names as patrilineal (passed from father to son), while offspring are randomly either male or female, and names become extinct if the family name line dies out (holders of the family name die without male descendants). This is an accurate description of Y chromosome transmission in genetics, and the model is thus useful for understanding human Y-chromosome DNA haplogroups. Likewise, since mitochondria are inherited only on the maternal line, the same mathematical formulation describes transmission of mitochondria. The formula is of limited usefulness in understanding actual family name distributions, since in practice family names change for many other reasons, and dying out of name line is only one factor.
History
There was concern amongst the Victorians that aristocratic surnames[example needed] were becoming extinct.
In 1869, Galton published Hereditary Genius, in which he treated the extinction of different social groups.
Galton originally posed a mathematical question regarding the distribution of surnames in an idealized population in an 1873 issue of The Educational Times:[1]
A large nation, of whom we will only concern ourselves with adult males, N in number, and who each bear separate surnames colonise a district. Their law of population is such that, in each generation, a0 per cent of the adult males have no male children who reach adult life; a1 have one such male child; a2 have two; and so on up to a5 who have five. Find what proportion of their surnames will have become extinct after r generations; and how many instances there will be of the surname being held by m persons.
The Reverend Henry William Watson replied with a solution.[2] Together, they then wrote an 1874 paper titled "On the probability of the extinction of families" in the Journal of the Anthropological Institute of Great Britain and Ireland (now the Journal of the Royal Anthropological Institute).[3] Galton and Watson appear to have derived their process independently of the earlier work by I. J. Bienaymé; see.[4] Their solution is incomplete, according to which all family names go extinct with probability 1.
Bienaymé published the answer to the problem in 1845,[5] with a promise to publish the derivation later. though there is no known publication of his solution. (However, Bru (1991)[6] purports to reconstruct the proof). He was inspired by Émile Littré[7] and Louis-François Benoiston de Châteauneuf (a friend of Bienaymé)[8].[9]
Cournot published a solution in 1847, in chapter 36 of.[10] The problem in his formulation is
- Consider a gambler who buys lotteries. Each lottery costs 1 ecu and pays [math]\displaystyle{ 0, 1, ..., n }[/math] with probabilities [math]\displaystyle{ p_0, ..., p_n }[/math]. The gambler always spends all their money to buy lotteries. If the gambler starts with [math]\displaystyle{ k }[/math] dollars, what's the probability of going bankrupt?
Ronald A. Fisher in 1922 studied the same problem formulated in terms of genetics. Instead of the extinction of family names, he studied the probability for a mutant gene to eventually disappear in a large population.[11] Haldane solved the problem in 1927.[12]
Agner Krarup Erlang was a member of the prominent Krarup family, which was going extinct. In 1929, he published the same problem posthumously (his obituary appears beside the problem). Erlang died childless. Steffensen solved it in 1930.
For a detailed history, see Kendall (1966[13] and 1975[9]) and [14] and also Section 17 of.[15]
Concepts
Assume, for the sake of the model, that surnames are passed on to all male children by their father. Suppose the number of a man's sons to be a random variable distributed on the set { 0, 1, 2, 3, ... }. Further suppose the numbers of different men's sons to be independent random variables, all having the same distribution.
Then the simplest substantial mathematical conclusion is that if the average number of a man's sons is 1 or less, then their surname will almost surely die out, and if it is more than 1, then there is more than zero probability that it will survive for any given number of generations.
Modern applications include the survival probabilities for a new mutant gene, or the initiation of a nuclear chain reaction, or the dynamics of disease outbreaks in their first generations of spread, or the chances of extinction of small population of organisms; as well as explaining (perhaps closest to Galton's original interest) why only a handful of males in the deep past of humanity now have any surviving male-line descendants, reflected in a rather small number of distinctive human Y-chromosome DNA haplogroups.
A corollary of high extinction probabilities is that if a lineage has survived, it is likely to have experienced, purely by chance, an unusually high growth rate in its early generations at least when compared to the rest of the population.
Mathematical definition
A Galton–Watson process is a stochastic process {Xn} which evolves according to the recurrence formula X0 = 1 and
- [math]\displaystyle{ X_{n+1} = \sum_{j=1}^{X_n} \xi_j^{(n)} }[/math]
where [math]\displaystyle{ \{\xi_j^{(n)} : n,j \in \mathbb{N}\} }[/math] is a set of independent and identically-distributed natural number-valued random variables.
In the analogy with family names, Xn can be thought of as the number of descendants (along the male line) in the nth generation, and [math]\displaystyle{ \xi_j^{(n)} }[/math] can be thought of as the number of (male) children of the jth of these descendants. The recurrence relation states that the number of descendants in the n+1st generation is the sum, over all nth generation descendants, of the number of children of that descendant.
The extinction probability (i.e. the probability of final extinction) is given by
- [math]\displaystyle{ \lim_{n \to \infty} \Pr(X_n = 0).\, }[/math]
This is clearly equal to zero if each member of the population has exactly one descendant. Excluding this case (usually called the trivial case) there exists a simple necessary and sufficient condition, which is given in the next section.
Extinction criterion for Galton–Watson process
In the non-trivial case, the probability of final extinction is equal to 1 if E{ξ1} ≤ 1 and strictly less than 1 if E{ξ1} > 1.
The process can be treated analytically using the method of probability generating functions.
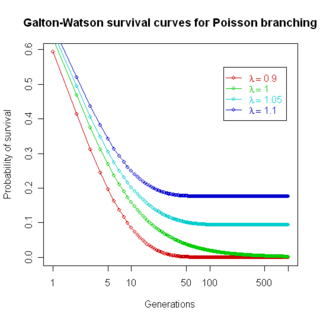
If the number of children ξ j at each node follows a Poisson distribution with parameter λ, a particularly simple recurrence can be found for the total extinction probability xn for a process starting with a single individual at time n = 0:
- [math]\displaystyle{ x_{n+1} = e^{\lambda (x_n - 1)},\, }[/math]
giving the above curves.
Bisexual Galton–Watson process
In the classical family surname Galton–Watson process described above, only men need to be considered, since only males transmit their family name to descendants. This effectively means that reproduction can be modeled as asexual. (Likewise, if mitochondrial transmission is analyzed, only women need to be considered, since only females transmit their mitochondria to descendants.)
A model more closely following actual sexual reproduction is the so-called "bisexual Galton–Watson process", where only couples reproduce.[citation needed] (Bisexual in this context refers to the number of sexes involved, not sexual orientation.) In this process, each child is supposed as male or female, independently of each other, with a specified probability, and a so-called "mating function" determines how many couples will form in a given generation. As before, reproduction of different couples are considered to be independent of each other. Now the analogue of the trivial case corresponds to the case of each male and female reproducing in exactly one couple, having one male and one female descendant, and that the mating function takes the value of the minimum of the number of males and females (which are then the same from the next generation onwards).
Since the total reproduction within a generation depends now strongly on the mating function, there exists in general no simple necessary and sufficient condition for final extinction as is the case in the classical Galton–Watson process.[citation needed] However, excluding the non-trivial case, the concept of the averaged reproduction mean (Bruss (1984)) allows for a general sufficient condition for final extinction, treated in the next section.
Extinction criterion
If in the non-trivial case the averaged reproduction mean per couple stays bounded over all generations and will not exceed 1 for a sufficiently large population size, then the probability of final extinction is always 1.
Examples
Citing historical examples of Galton–Watson process is complicated due to the history of family names often deviating significantly from the theoretical model. Notably, new names can be created, existing names can be changed over a person's lifetime, and people historically have often assumed names of unrelated persons, particularly nobility. Thus, a small number of family names at present is not in itself evidence for names having become extinct over time, or that they did so due to dying out of family name lines – that requires that there were more names in the past and that they die out due to the line dying out, rather than the name changing for other reasons, such as vassals assuming the name of their lord.
Chinese names are a well-studied example of surname extinction: there are currently only about 3,100 surnames in use in China, compared with close to 12,000 recorded in the past,[16][17] with 22% of the population sharing the names Li, Wang and Zhang (numbering close to 300 million people), and the top 200 names covering 96% of the population. Names have changed or become extinct for various reasons such as people taking the names of their rulers, orthographic simplifications, taboos against using characters from an emperor's name, among others.[17] While family name lines dying out may be a factor in the surname extinction, it is by no means the only or even a significant factor. Indeed, the most significant factor affecting the surname frequency is other ethnic groups identifying as Han and adopting Han names.[17] Further, while new names have arisen for various reasons, this has been outweighed by old names disappearing.[17]
By contrast, some nations have adopted family names only recently. This means both that they have not experienced surname extinction for an extended period, and that the names were adopted when the nation had a relatively large population, rather than the smaller populations of ancient times.[17] Further, these names have often been chosen creatively and are very diverse. Examples include:
- Japanese names, which in general use date only to the Meiji restoration in the late 19th century (when the population was over 30,000,000), have over 100,000 family names, surnames are very varied, and the government restricts married couples to using the same surname.
- Many Dutch names have included a formal family name only since the Napoleonic Wars in the early 19th century. Earlier, surnames originated from patronyms[18] (e.g., Jansen = John's son), personal qualities (e.g., de Rijke = the rich one), geographical locations (e.g., van Rotterdam), and occupations (e.g., Visser = the fisherman), sometimes even combined (e.g., Jan Jansz van Rotterdam). There are over 68,000 Dutch family names.
- Thai names have included a family name only since 1920, and only a single family can use a given family name; hence there are a great number of Thai names. Furthermore, Thai people change their family names with some frequency, complicating the analysis.
On the other hand, some examples of high concentration of family names is not primarily due to the Galton–Watson process:
- Vietnamese names have about 100 family names, with 60% of the population sharing three family names. The name Nguyễn alone is estimated to be used by almost 40% of the Vietnamese population, and 90% share 15 names. However, as the history of the Nguyễn name makes clear, this is in no small part due to names being forced on people or adopted for reasons unrelated to genetic relation.
See also
References
- ↑ Francis Galton (1873-03-01). "Problem 4001". Educational Times 25 (143): 300. Archived from the original on 2017-01-23. https://web.archive.org/web/20170123114453/http://ioearc.da.ulcc.ac.uk/9344/1/Educational%20Times%20Vol%2025%20Iss%20143.PDF.
- ↑ Henry William Watson (1873-08-01). "Problem 4001". Educational Times 26 (148): 115. Archived from the original on 2016-12-01. https://web.archive.org/web/20161201212518/http://ioearc.da.ulcc.ac.uk/9309/1/Educational%20Times%20Vol%2026%20Iss%20148.PDF.
A first offering submitted by G.S. Carr, according to Galton, was "totally erroneous"; see G. S. Carr (1873-04-01). "Problem 4001". Educational Times 26 (144): 17. Archived from the original on 2017-08-03. https://web.archive.org/web/20170803094523/http://ioearc.da.ulcc.ac.uk/9305/1/Educational%20Times%20Vol%2026%20Iss%20144.PDF. - ↑ Galton, F., & Watson, H. W. (1875). "On the probability of the extinction of families". Journal of the Royal Anthropological Institute, 4, 138–144.
- ↑ Heyde, C. C.; Seneta, E. (1972). "Studies in the History of Probability and Statistics. XXXI. The simple branching process, a turning point test and a fundamental inequality: A historical note on I. J. Bienaymé" (in en). Biometrika 59 (3): 680–683. doi:10.1093/biomet/59.3.680. ISSN 0006-3444. https://academic.oup.com/biomet/article-lookup/doi/10.1093/biomet/59.3.680.
- ↑ Bienayme, I.J. (1845). De la loi de multiplication et de la durée des families. L’Institut, 589, Vol. 13, pp. 131–132. Soc. Philomat. Paris Extraits, Ser. 5, 37–39. (Reprinted in Kendall, D. G. (1975))
- ↑ Bru, Bernard. "A la recherche de la démonstration perdue de Bienaymé." Mathématiques et Sciences humaines 114 (1991): 5-17.
- ↑ Littré, Émile. Analyse raisonnée du cours de philosophie positive de M. Auguste Comte. 1845.
- ↑ L. F. Benoiston de Châteauneuf, "Sur la durée des familles nobles de France," Séances et Travaux de l'Académie des Sciences Morales et Politiques: Comptes Rendus, 7 (1845), 210-240.
- ↑ 9.0 9.1 Kendall, David G. (November 1975). "The Genealogy of Genealogy Branching Processes before (and after) 1873" (in en). Bulletin of the London Mathematical Society 7 (3): 225–253. doi:10.1112/blms/7.3.225. http://doi.wiley.com/10.1112/blms/7.3.225.
- ↑ Cournot, A. A. (Antoine Augustin) (1847). De l'origine et des limites de la correspondance entre l'algèbre et la géométrie. University of Illinois Urbana-Champaign. Paris : L. Hachette. http://archive.org/details/delorigineetdesl00cour.
- ↑ Fisher, R. A. (1922). "XXI.—On the Dominance Ratio" (in en). Proceedings of the Royal Society of Edinburgh 42: 321–341. doi:10.1017/S0370164600023993. ISSN 0370-1646. https://www.cambridge.org/core/journals/proceedings-of-the-royal-society-of-edinburgh/article/abs/xxion-the-dominance-ratio/2CDBE1D374EBE9B2774DF301BA98A584.
- ↑ Haldane, J. B. S. (July 1927). "A Mathematical Theory of Natural and Artificial Selection, Part V: Selection and Mutation" (in en). Mathematical Proceedings of the Cambridge Philosophical Society 23 (7): 838–844. doi:10.1017/S0305004100015644. ISSN 1469-8064. Bibcode: 1927PCPS...23..838H. https://www.cambridge.org/core/journals/mathematical-proceedings-of-the-cambridge-philosophical-society/article/abs/mathematical-theory-of-natural-and-artificial-selection-part-v-selection-and-mutation/9B6F4FE68136A70E06133E2E389EFA5B.
- ↑ Kendall, David G. (1966). "Branching Processes Since 1873" (in en). Journal of the London Mathematical Society s1-41 (1): 385–406. doi:10.1112/jlms/s1-41.1.385. http://doi.wiley.com/10.1112/jlms/s1-41.1.385.
- ↑ Albertsen, K. (1995). "The Extinction of Families". International Statistical Review / Revue Internationale de Statistique 63 (2): 234–239. doi:10.2307/1403617. ISSN 0306-7734. https://www.jstor.org/stable/1403617.
- ↑ Simkin, M. V.; Roychowdhury, V. P. (2011-05-01). "Re-inventing Willis" (in en). Physics Reports 502 (1): 1–35. doi:10.1016/j.physrep.2010.12.004. ISSN 0370-1573. Bibcode: 2011PhR...502....1S. https://www.sciencedirect.com/science/article/pii/S0370157310003339.
- ↑ "O rare John Smith", The Economist: 32, June 3, 1995, "Only 3,100 surnames are now in use in China [...] compared with nearly 12,000 in the past. An 'evolutionary dwindling' of surnames is common to all societies. [...] [B]ut in China, [Du] says, where surnames have been in use far longer than in most other places, the paucity has become acute."
- ↑ 17.0 17.1 17.2 17.3 17.4 Du, Ruofu; Yida, Yuan; Hwang, Juliana; Mountain, Joanna L.; Cavalli-Sforza, L. Luca (1992), Chinese Surnames and the Genetic Differences between North and South China, Journal of Chinese Linguistics Monograph Series, pp. 18–22 (History of Chinese surnames and sources of data for the present research), archived from the original on 2012-11-20, https://web.archive.org/web/20121120173231/http://hsblogs.stanford.edu/morrison/files/2011/02/27.pdf, also part of Morrison Institute for Population and Resource Studies Working papers
- ↑ "Patronym - Behind the Name". https://surnames.behindthename.com/glossary/view/patronym.
Further reading
- F. Thomas Bruss (1984). "A Note on Extinction Criteria for Bisexual Galton–Watson Processes". Journal of Applied Probability 21: 915–919.
- C C Heyde and E Seneta (1977). I.J. Bienayme: Statistical Theory Anticipated. Berlin, Germany.
- Kendall, D. G. (1966). "Branching Processes Since 1873". Journal of the London Mathematical Society s1-41: 385–406. doi:10.1112/jlms/s1-41.1.385. ISSN 0024-6107.
- Kendall, D. G. (1975). "The Genealogy of Genealogy Branching Processes before (and after) 1873". Bulletin of the London Mathematical Society 7 (3): 225–253. doi:10.1112/blms/7.3.225. ISSN 0024-6093.
External links
- "Survival of a Single Mutant" by Peter M. Lee of the University of York
- The simple Galton-Watson process: Classical approach, University of Muenster
 |

