Michael selection theorem
In functional analysis, a branch of mathematics, Michael selection theorem is a selection theorem named after Ernest Michael. In its most popular form, it states the following:[1]
- Let X be a paracompact space and Y a Banach space.
- Let [math]\displaystyle{ F\colon X\to Y }[/math] be a lower hemicontinuous set-valued function with nonempty convex closed values.
- Then there exists a continuous selection [math]\displaystyle{ f\colon X \to Y }[/math] of F.
- Conversely, if any lower semicontinuous multimap from topological space X to a Banach space, with nonempty convex closed values, admits a continuous selection, then X is paracompact. This provides another characterization for paracompactness.
Examples
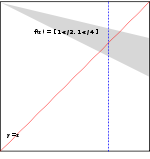
A function that satisfies all requirements
The function: [math]\displaystyle{ F(x)= [1-x/2, ~1-x/4] }[/math], shown by the grey area in the figure at the right, is a set-valued function from the real interval [0,1] to itself. It satisfies all Michael's conditions, and indeed it has a continuous selection, for example: [math]\displaystyle{ f(x)= 1-x/2 }[/math] or [math]\displaystyle{ f(x)= 1-3x/8 }[/math].
A function that does not satisfy lower hemicontinuity
The function
[math]\displaystyle{ F(x)= \begin{cases} 3/4 & 0 \le x \lt 0.5 \\ \left[0,1\right] & x = 0.5 \\ 1/4 & 0.5 \lt x \le 1 \end{cases} }[/math]
is a set-valued function from the real interval [0,1] to itself. It has nonempty convex closed values. However, it is not lower hemicontinuous at 0.5. Indeed, Michael's theorem does not apply and the function does not have a continuous selection: any selection at 0.5 is necessarily discontinuous.[2]
Applications
Michael selection theorem can be applied to show that the differential inclusion
- [math]\displaystyle{ \frac{dx}{dt}(t)\in F(t,x(t)), \quad x(t_0)=x_0 }[/math]
has a C1 solution when F is lower semi-continuous and F(t, x) is a nonempty closed and convex set for all (t, x). When F is single valued, this is the classic Peano existence theorem.
Generalizations
A theorem due to Deutsch and Kenderov generalizes Michel selection theorem to an equivalence relating approximate selections to almost lower hemicontinuity, where [math]\displaystyle{ F }[/math] is said to be almost lower hemicontinuous if at each [math]\displaystyle{ x \in X }[/math], all neighborhoods [math]\displaystyle{ V }[/math] of [math]\displaystyle{ 0 }[/math] there exists a neighborhood [math]\displaystyle{ U }[/math] of [math]\displaystyle{ x }[/math] such that [math]\displaystyle{ \cap_{u\in U} \{F(u)+V\} \ne \emptyset. }[/math]
Precisely, Deutsch–Kenderov theorem states that if [math]\displaystyle{ X }[/math] is paracompact, [math]\displaystyle{ Y }[/math] a normed vector space and [math]\displaystyle{ F (x) }[/math] is nonempty convex for each [math]\displaystyle{ x \in X }[/math], then [math]\displaystyle{ F }[/math] is almost lower hemicontinuous if and only if [math]\displaystyle{ F }[/math] has continuous approximate selections, that is, for each neighborhood [math]\displaystyle{ V }[/math] of [math]\displaystyle{ 0 }[/math] in [math]\displaystyle{ Y }[/math] there is a continuous function [math]\displaystyle{ f \colon X \mapsto Y }[/math] such that for each [math]\displaystyle{ x \in X }[/math], [math]\displaystyle{ f (x) \in F (X) + V }[/math].[3]
In a note Xu proved that Deutsch–Kenderov theorem is also valid if [math]\displaystyle{ Y }[/math] is a locally convex topological vector space.[4]
See also
- Zero-dimensional Michael selection theorem
- Selection theorem
References
- ↑ Michael, Ernest (1956). "Continuous selections. I". Annals of Mathematics. Second Series 63 (2): 361–382. doi:10.2307/1969615.
- ↑ "proof verification - Reducing Kakutani's fixed-point theorem to Brouwer's using a selection theorem". https://math.stackexchange.com/q/3377063.
- ↑ Deutsch, Frank; Kenderov, Petar (January 1983). "Continuous Selections and Approximate Selection for Set-Valued Mappings and Applications to Metric Projections". SIAM Journal on Mathematical Analysis 14 (1): 185–194. doi:10.1137/0514015.
- ↑ Xu, Yuguang (December 2001). "A Note on a Continuous Approximate Selection Theorem". Journal of Approximation Theory 113 (2): 324–325. doi:10.1006/jath.2001.3622.
Further reading
- Repovš, Dušan; Semenov, Pavel V. (2014). "Continuous Selections of Multivalued Mappings". in Hart, K. P.; van Mill, J.; Simon, P.. Recent Progress in General Topology. III. Berlin: Springer. pp. 711–749. ISBN 978-94-6239-023-2. Bibcode: 2014arXiv1401.2257R.
- Aubin, Jean-Pierre; Cellina, Arrigo (1984). Differential Inclusions, Set-Valued Maps And Viability Theory. Grundl. der Math. Wiss.. 264. Berlin: Springer-Verlag. ISBN 3-540-13105-1.
- Aubin, Jean-Pierre; Frankowska, H. (1990). Set-Valued Analysis. Basel: Birkhäuser. ISBN 3-7643-3478-9.
- Deimling, Klaus (1992). Multivalued Differential Equations. Walter de Gruyter. ISBN 3-11-013212-5.
- Repovš, Dušan; Semenov, Pavel V. (1998). Continuous Selections of Multivalued Mappings. Dordrecht: Kluwer Academic Publishers. ISBN 0-7923-5277-7.
- Repovš, Dušan; Semenov, Pavel V. (2008). "Ernest Michael and Theory of Continuous Selections". Topology and its Applications 155 (8): 755–763. doi:10.1016/j.topol.2006.06.011.
- Aliprantis, Charalambos D.; Border, Kim C. (2007). Infinite Dimensional Analysis : Hitchhiker's Guide (3rd ed.). Springer. ISBN 978-3-540-32696-0.
- Hu, S.; Papageorgiou, N.. Handbook of Multivalued Analysis. I. Kluwer. ISBN 0-7923-4682-3.
 |