Astronomy:Spaghettification

From HandWiki
Short description: Phenomenon in astrophysics
Astronaut falling into a black hole (schematic illustration of the spaghettification effect)
Tidal forces acting on a spherical body in a non-homogeneous gravitational field. In this diagram, the gravitational force originates from a source to the right. It shows both the tidal field (thick red arrows) and the gravity field (thin blue arrows) exerted on the body's surface and center (label O) by a source (label S).

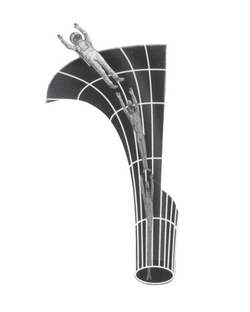
In astrophysics, spaghettification (sometimes referred to as the noodle effect)[1] is the vertical stretching and horizontal compression of objects into long thin shapes (rather like spaghetti) in a very strong, non-homogeneous gravitational field. It is caused by extreme tidal forces. In the most extreme cases, near a black hole, the stretching and compression are so powerful that no object can resist it. Within a small region, the horizontal compression balances the vertical stretching so that a small object being spaghettified experiences no net change in volume.

Stephen Hawking described the flight of a fictional astronaut who, passing within a black hole's event horizon, is "stretched like spaghetti" by the gravitational gradient (difference in gravitational force) from head to toe.[2] The reason this happens would be that the gravitational force exerted by the singularity would be much stronger at one end of the body than the other. If one were to fall into a black hole feet first, the gravity at their feet would be much stronger than at their head, causing the person to be vertically stretched. Along with that, the right side of the body will be pulled to the left, and the left side of the body will be pulled to the right, horizontally compressing the person.[3] However, the term spaghettification was established well before this.[4] Spaghettification of a star was imaged for the first time in 2018 by researchers observing a pair of colliding galaxies approximately 150 million light-years from Earth.[5]

A simple example

The spaghettification of four objects falling towards a planet

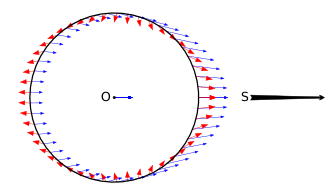
In this example, four separate objects are in the space above a planet, positioned in a diamond formation. The four objects follow the lines of the gravitoelectric field,[6] directed towards the celestial body's centre. In accordance with the inverse-square law, the lowest of the four objects experiences the biggest gravitational acceleration, so that the whole formation becomes stretched into a line.

These four objects are connected parts of a larger object. A rigid body will resist distortion, and internal elastic forces develop as the body distorts to balance the tidal forces, so attaining mechanical equilibrium. If the tidal forces are too large, the body may yield and flow plastically before the tidal forces can be balanced, or fracture, producing either a filament or a vertical line of broken pieces.

Examples of weak and strong tidal forces

In the gravity field due to a point mass or spherical mass, for a uniform rod oriented in the direction of gravity, the tensile force at the center is found by integration of the tidal force from the center to one of the ends. This gives F = μ l m/4r3, where μ is the standard gravitational parameter of the massive body, l is the length of the rod, m is rod's mass, and r is the distance to the massive body. For non-uniform objects the tensile force is smaller if more mass is near the center, and up to twice as large if more mass is at the ends. In addition, there is a horizontal compression force toward the center.

For massive bodies with a surface, the tensile force is largest near the surface, and this maximum value is only dependent on the object and the average density of the massive body (as long as the object is small relative to the massive body). For example, for a rod with a mass of 1 kg and a length of 1 m, and a massive body with the average density of the Earth, this maximum tensile force due to the tidal force is only 0.4 μN.

Due to the high density, the tidal force near the surface of a white dwarf is much stronger, causing in the example a maximum tensile force of up to 0.24 N. Near a neutron star, the tidal forces are again much stronger: if the rod has a tensile strength of 10,000 N and falls vertically to a neutron star of 2.1 solar masses, setting aside that it would melt, it would break at a distance of 190 km from the center, well above the surface (a neutron star typically has a radius of only about 12 km).[note 1]

In the previous case, objects would actually be destroyed and people killed by the heat, not the tidal forces - but near a black hole (assuming that there is no nearby matter), objects would actually be destroyed and people killed by the tidal forces because there is no radiation. Moreover, a black hole has no surface to stop a fall. Thus, the infalling object is stretched into a thin strip of matter.

Inside or outside the event horizon

Close-up of star near a supermassive black hole (artist's impression).[7]

The point at which tidal forces destroy an object or kill a person will depend on the black hole's size. For a supermassive black hole, such as those found at a galaxy's center, this point lies within the event horizon, so an astronaut may cross the event horizon without noticing any squashing and pulling, although it remains only a matter of time, as once inside an event horizon, falling towards the center is inevitable.[8] For small black holes whose Schwarzschild radius is much closer to the singularity, the tidal forces would kill even before the astronaut reaches the event horizon.[9][10] For example, for a black hole of 10 Sun masses[note 2] the above-mentioned rod breaks at a distance of 320 km, well outside the Schwarzschild radius of 30 km. For a supermassive black hole of 10,000 Sun masses, it will break at a distance of 3,200 km, well inside the Schwarzschild radius of 30,000 km.

Notes

  1. ↑ An 8-meter rod of the same strength, with a mass of 8 kg, breaks at a distance 4 times as high.[citation needed]
  2. ↑ The smallest black hole that can be formed by natural processes at the current stage of the universe has over twice the mass of the Sun.[citation needed]

References

Inline citations
  1. ↑ Wheeler, J. Craig (2007), Cosmic catastrophes: exploding stars, black holes, and mapping the universe (2nd ed.), Cambridge University Press, p. 182, ISBN 978-0-521-85714-7, https://books.google.com/books?id=j1ej8d0F8jAC 
  2. ↑ Hawking, Stephen (1988). A Brief History of Time. Bantam Dell Publishing Group. pp. 256. ISBN 978-0-553-10953-5. 
  3. ↑ Astronomy. OpenStax. 2016. pp. 862. ISBN 978-1938168284. 
  4. ↑ Calder, Nigel (1977). The Key to the Universe: A Report on the New Physics. Viking Press. p. 143. ISBN 978-0-67041270-9. https://archive.org/details/keytouniverserep0000cald/page/143. Retrieved July 10, 2022.  Published as a companion to the BBC TV documentary The Key to the Universe.
  5. ↑ "Astronomers See Distant Eruption as Black Hole Destroys Star" (Press release). National Radio Astronomy Observatory. Phys.org. 2018-06-14. Retrieved 2018-06-15.
  6. ↑ Thorne, Kip S. (1988). "Gravitomagnetism, Jets in Quasars, and the Stanford Gyroscope Experiment". in Fairbank, J. D.; Deaver, Jr., B. S.; Everitt, C. F. et al.. Near Zero: New Frontiers of Physics. New York City: W. H. Freeman and Company. pp. 3, 4 (575, 576). http://einstein.stanford.edu/content/sci_papers/papers/nz-Thorne_101.pdf#page=3&view=FitV. "From our electrodynamical experience we can infer immediately that any rotating spherical body (e.g., the sun or the earth) will be surrounded by a radial gravitoelectric (Newtonian) field g and a dipolar gravitomagnetic field H. The gravitoelectric monopole moment is the body's mass M; the gravitomagnetic dipole moment is its spin angular momentum S." 
  7. ↑ "Spinning Black Hole Swallowing Star Explains Superluminous Event - ESO telescopes help reinterpret brilliant explosion". https://www.eso.org/public/news/eso1644/. 
  8. ↑ Hawley, John F.; Holcomb, Katherine A. (2005). Foundations of Modern Cosmology (illustrated ed.). Oxford University Press. p. 253. ISBN 978-0-19-853096-1. https://books.google.com/books?id=s5MUDAAAQBAJ.  Extract of page 253
  9. ↑ Hobson, Michael Paul; Efstathiou, George; Lasenby, Anthony N. (2006). "11. Schwarzschild black holes". General relativity: an introduction for physicists. Cambridge University Press. p. 265. ISBN 0-521-82951-8. https://books.google.com/books?id=5dryXCWR7EIC&pg=PA265. 
  10. ↑ Kutner, Marc Leslie (2003). "8. General relativity". Astronomy: a physical perspective (2nd ed.). Cambridge University Press. p. 150. ISBN 0-521-52927-1. https://books.google.com/books?id=2QVmiMW0O0MC&pg=PA150. 
General references

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Astronomy:Spaghettification&oldid=3344343"