Astronomy:Accretion disk
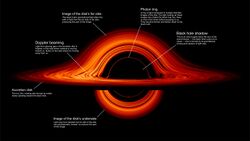
An accretion disk is a structure (often a circumstellar disk) formed by diffuse material[lower-alpha 1] in orbital motion around a massive central body. The central body is most frequently a star. Friction, uneven irradiance, magnetohydrodynamic effects, and other forces induce instabilities causing orbiting material in the disk to spiral inward toward the central body. Gravitational and frictional forces compress and raise the temperature of the material, causing the emission of electromagnetic radiation. The frequency range of that radiation depends on the central object's mass. Accretion disks of young stars and protostars radiate in the infrared; those around neutron stars and black holes in the X-ray part of the spectrum. The study of oscillation modes in accretion disks is referred to as diskoseismology.[1][2]
Manifestations
| Unsolved problem in physics: Accretion disk jets: Why do the disks surrounding certain objects, such as the nuclei of active galaxies, emit jets along their polar axes? These jets are invoked by astronomers to do everything from getting rid of angular momentum in a forming star to reionizing the universe (in active galactic nuclei), but their origin is still not well understood. (more unsolved problems in physics)
|
Accretion disks are a ubiquitous phenomenon in astrophysics; active galactic nuclei, protoplanetary disks, and gamma ray bursts all involve accretion disks. These disks very often give rise to astrophysical jets coming from the vicinity of the central object. Jets are an efficient way for the star-disk system to shed angular momentum without losing too much mass.
The most spectacular accretion disks found in nature are those of active galactic nuclei and of quasars, which are thought to be massive black holes at the center of galaxies. As matter enters the accretion disc, it follows a trajectory called a tendex line, which describes an inward spiral. This is because particles rub and bounce against each other in a turbulent flow, causing frictional heating which radiates energy away, reducing the particles' angular momentum, allowing the particle to drift inward, driving the inward spiral. The loss of angular momentum manifests as a reduction in velocity; at a slower velocity, the particle must adopt a lower orbit. As the particle falls to this lower orbit, a portion of its gravitational potential energy is converted to increased velocity and the particle gains speed. Thus, the particle has lost energy even though it is now travelling faster than before; however, it has lost angular momentum. As a particle orbits closer and closer, its velocity increases; as velocity increases frictional heating increases as more and more of the particle's potential energy (relative to the black hole) is radiated away; the accretion disk of a black hole is hot enough to emit X-rays just outside the event horizon. The large luminosity of quasars is believed to be a result of gas being accreted by supermassive black holes.[3] Elliptical accretion disks formed at tidal disruption of stars can be typical in galactic nuclei and quasars.[4] The accretion process can convert about 10 percent to over 40 percent of the mass of an object into energy as compared to around 0.7 percent for nuclear fusion processes.[5] In close binary systems the more massive primary component evolves faster and has already become a white dwarf, a neutron star, or a black hole, when the less massive companion reaches the giant state and exceeds its Roche lobe. A gas flow then develops from the companion star to the primary. Angular momentum conservation prevents a straight flow from one star to the other and an accretion disk forms instead.
Accretion disks surrounding T Tauri stars or Herbig stars are called protoplanetary disks because they are thought to be the progenitors of planetary systems. The accreted gas in this case comes from the molecular cloud out of which the star has formed rather than a companion star.

Accretion disk physics

In the 1940s, models were first derived from basic physical principles.[6] In order to agree with observations, those models had to invoke a yet unknown mechanism for angular momentum redistribution. If matter is to fall inward it must lose not only gravitational energy but also lose angular momentum. Since the total angular momentum of the disk is conserved, the angular momentum loss of the mass falling into the center has to be compensated by an angular momentum gain of the mass far from the center. In other words, angular momentum should be transported outward for matter to accrete. According to the Rayleigh stability criterion,
where represents the angular velocity of a fluid element and its distance to the rotation center, an accretion disk is expected to be a laminar flow. This prevents the existence of a hydrodynamic mechanism for angular momentum transport.
On one hand, it was clear that viscous stresses would eventually cause the matter toward the center to heat up and radiate away some of its gravitational energy. On the other hand, viscosity itself was not enough to explain the transport of angular momentum to the exterior parts of the disk. Turbulence-enhanced viscosity was the mechanism thought to be responsible for such angular-momentum redistribution, although the origin of the turbulence itself was not well understood. The conventional -model (discussed below) introduces an adjustable parameter describing the effective increase of viscosity due to turbulent eddies within the disk.[7][8] In 1991, with the rediscovery of the magnetorotational instability (MRI), S. A. Balbus, and J. F. Hawley established that a weakly magnetized disk accreting around a heavy, compact central object would be highly unstable, providing a direct mechanism for angular-momentum redistribution.[9]
α-Disk model
Shakura and Sunyaev (1973)[7] proposed turbulence in the gas as the source of an increased viscosity. Assuming subsonic turbulence and the disk height as an upper limit for the size of the eddies, the disk viscosity can be estimated as where is the sound speed, is the scale height of the disk, and is a free parameter between zero (no accretion) and approximately one. In a turbulent medium , where is the velocity of turbulent cells relative to the mean gas motion, and is the size of the largest turbulent cells, which is estimated as and , where is the Keplerian orbital angular velocity, is the radial distance from the central object of mass .[10] By using the equation of hydrostatic equilibrium, combined with conservation of angular momentum and assuming that the disk is thin, the equations of disk structure may be solved in terms of the parameter. Many of the observables depend only weakly on , so this theory is predictive even though it has a free parameter.
Using Kramers' opacity law it is found that
where and are the mid-plane temperature and density respectively. is the accretion rate, in units of , is the mass of the central accreting object in units of a solar mass, , is the radius of a point in the disk, in units of , and , where is the radius where angular momentum stops being transported inward.
The Shakura–Sunyaev α-disk model is both thermally and viscously unstable. An alternative model, known as the -disk, which is stable in both senses assumes that the viscosity is proportional to the gas pressure .[11][12] In the standard Shakura–Sunyaev model, viscosity is assumed to be proportional to the total pressure since .
The Shakura–Sunyaev model assumes that the disk is in local thermal equilibrium, and can radiate its heat efficiently. In this case, the disk radiates away the viscous heat, cools, and becomes geometrically thin. However, this assumption may break down. In the radiatively inefficient case, the disk may "puff up" into a torus or some other three-dimensional solution like an Advection Dominated Accretion Flow (ADAF). The ADAF solutions usually require that the accretion rate is smaller than a few percent of the Eddington limit. Another extreme is the case of Saturn's rings, where the disk is so gas poor that its angular momentum transport is dominated by solid body collisions and disk-moon gravitational interactions. The model is in agreement with recent astrophysical measurements using gravitational lensing.[13][14][15][16]
Magnetorotational instability
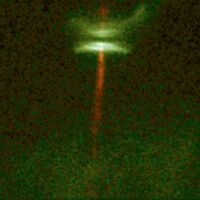
Balbus and Hawley (1991)[9] proposed a mechanism which involves magnetic fields to generate the angular momentum transport. A simple system displaying this mechanism is a gas disk in the presence of a weak axial magnetic field. Two radially neighboring fluid elements will behave as two mass points connected by a massless spring, the spring tension playing the role of the magnetic tension. In a Keplerian disk the inner fluid element would be orbiting more rapidly than the outer, causing the spring to stretch. The inner fluid element is then forced by the spring to slow down, reduce correspondingly its angular momentum causing it to move to a lower orbit. The outer fluid element being pulled forward will speed up, increasing its angular momentum and move to a larger radius orbit. The spring tension will increase as the two fluid elements move further apart and the process runs away.[17]
It can be shown that in the presence of such a spring-like tension the Rayleigh stability criterion is replaced by
Most astrophysical disks do not meet this criterion and are therefore prone to this magnetorotational instability. The magnetic fields present in astrophysical objects (required for the instability to occur) are believed to be generated via dynamo action.[18]
Magnetic fields and jets
Accretion disks are usually assumed to be threaded by the external magnetic fields present in the interstellar medium. These fields are typically weak (about few micro-Gauss), but they can get anchored to the matter in the disk, because of its high electrical conductivity, and carried inward toward the central star. This process can concentrate the magnetic flux around the centre of the disk giving rise to very strong magnetic fields. Formation of powerful astrophysical jets along the rotation axis of accretion disks requires a large scale poloidal magnetic field in the inner regions of the disk.[19]
Such magnetic fields may be advected inward from the interstellar medium or generated by a magnetic dynamo within the disk. Magnetic fields strengths at least of order 100 Gauss seem necessary for the magneto-centrifugal mechanism to launch powerful jets. There are problems, however, in carrying external magnetic flux inward toward the central star of the disk.[20] High electric conductivity dictates that the magnetic field is frozen into the matter which is being accreted onto the central object with a slow velocity. However, the plasma is not a perfect electric conductor, so there is always some degree of dissipation. The magnetic field diffuses away faster than the rate at which it is being carried inward by accretion of matter.[21] A simple solution is assuming a viscosity much larger than the magnetic diffusivity in the disk. However, numerical simulations and theoretical models show that the viscosity and magnetic diffusivity have almost the same order of magnitude in magneto-rotationally turbulent disks.[22] Some other factors may possibly affect the advection/diffusion rate: reduced turbulent magnetic diffusion on the surface layers; reduction of the Shakura–Sunyaev viscosity by magnetic fields;[23] and the generation of large scale fields by small scale MHD turbulence –a large scale dynamo. In fact, a combination of different mechanisms might be responsible for efficiently carrying the external field inward toward the central parts of the disk where the jet is launched. Magnetic buoyancy, turbulent pumping and turbulent diamagnetism exemplify such physical phenomena invoked to explain such efficient concentration of external fields.[24]
Analytic models of sub-Eddington accretion disks (thin disks, ADAFs)
When the accretion rate is sub-Eddington and the opacity very high, the standard thin accretion disk is formed. It is geometrically thin in the vertical direction (has a disk-like shape), and is made of a relatively cold gas, with a negligible radiation pressure. The gas goes down on very tight spirals, resembling almost circular, almost free (Keplerian) orbits. Thin disks are relatively luminous and they have thermal electromagnetic spectra, i.e. not much different from that of a sum of black bodies. Radiative cooling is very efficient in thin disks. The classic 1974 work by Shakura and Sunyaev on thin accretion disks is one of the most often quoted papers in modern astrophysics. Thin disks were independently worked out by Lynden-Bell, Pringle, and Rees. Pringle contributed in the past thirty years many key results to accretion disk theory, and wrote the classic 1981 review that for many years was the main source of information about accretion disks, and is still very useful today.

A fully general relativistic treatment, as needed for the inner part of the disk when the central object is a black hole, has been provided by Page and Thorne,[25] and used for producing simulated optical images by Luminet[26] and Marck,[27] in which, although such a system is intrinsically symmetric its image is not, because the relativistic rotation speed needed for centrifugal equilibrium in the very strong gravitational field near the black hole produces a strong Doppler redshift on the receding side (taken here to be on the right) whereas there will be a strong blueshift on the approaching side. Due to light bending, the disk appears distorted but is nowhere hidden by the black hole.
When the accretion rate is sub-Eddington and the opacity very low, an ADAF (advection dominated accretion flow) is formed. This type of accretion disk was predicted in 1977 by Ichimaru. Although Ichimaru's paper was largely ignored, some elements of the ADAF model were present in the influential 1982 ion-tori paper by Rees, Phinney, Begelman, and Blandford. ADAFs started to be intensely studied by many authors only after their rediscovery in the mid-1990 by Narayan and Yi, and independently by Abramowicz, Chen, Kato, Lasota (who coined the name ADAF), and Regev. Most important contributions to astrophysical applications of ADAFs have been made by Narayan and his collaborators. ADAFs are cooled by advection (heat captured in matter) rather than by radiation. They are very radiatively inefficient, geometrically extended, similar in shape to a sphere (or a "corona") rather than a disk, and very hot (close to the virial temperature). Because of their low efficiency, ADAFs are much less luminous than the Shakura–Sunyaev thin disks. ADAFs emit a power-law, non-thermal radiation, often with a strong Compton component.
Credit: NASA/JPL-Caltech
Analytic models of super-Eddington accretion disks (slim disks, Polish doughnuts)
The theory of highly super-Eddington black hole accretion, M≫MEdd, was developed in the 1980s by Abramowicz, Jaroszynski, Paczyński, Sikora, and others in terms of "Polish doughnuts" (the name was coined by Rees). Polish doughnuts are low viscosity, optically thick, radiation pressure supported accretion disks cooled by advection. They are radiatively very inefficient. Polish doughnuts resemble in shape a fat torus (a doughnut) with two narrow funnels along the rotation axis. The funnels collimate the radiation into beams with highly super-Eddington luminosities.
Slim disks (name coined by Kolakowska) have only moderately super-Eddington accretion rates, M≥MEdd, rather disk-like shapes, and almost thermal spectra. They are cooled by advection, and are radiatively ineffective. They were introduced by Abramowicz, Lasota, Czerny, and Szuszkiewicz in 1988.
| Unsolved problem in physics: Accretion disk QPOs: Quasi-periodic oscillations happen in many accretion disks, with their periods appearing to scale as the inverse of the mass of the central object. Why do these oscillations exist? Why are there sometimes overtones, and why do these appear at different frequency ratios in different objects? (more unsolved problems in physics)
|
Excretion disk
The opposite of an accretion disk is an excretion disk where instead of material accreting from a disk on to a central object, material is excreted from the center outward onto the disk. Excretion disks are formed when stars merge.[29]
See also
- Accretion
- Astrophysical jet
- Blandford–Znajek process
- Circumstellar disc
- Circumplanetary disk
- Dynamo theory
- Exoasteroid
- Gravitational singularity
- Quasi-star
- Ring system
- Solar nebula
- Spin-flip
Notes
- ↑ In astrophysics, diffuse material refers to interstellar or intergalactic matter that is spread out and not concentrated in a specific location. This material can include gas, dust, and other particles that are not organized into distinct structures like stars or galaxies.
References
- ↑ Nowak, Michael A.; Wagoner, Robert V. (1991). "Diskoseismology: Probing accretion disks. I - Trapped adiabatic oscillations". Astrophysical Journal 378: 656–664. doi:10.1086/170465. Bibcode: 1991ApJ...378..656N.
- ↑ Wagoner, Robert V. (2008). "Relativistic and Newtonian diskoseismology". New Astronomy Reviews 51 (10–12): 828–834. doi:10.1016/j.newar.2008.03.012. Bibcode: 2008NewAR..51..828W.
- ↑ Lynden-Bell, D. (1969). "Galactic Nuclei as Collapsed Old Quasars". Nature 280 (5207): 690–694. doi:10.1038/223690a0. Bibcode: 1969Natur.223..690L.
- ↑ Gurzadyan, V. G.; Ozernoy, L. M. (1979). "Accretion on massive black holes in galactic nuclei". Nature 280 (5719): 214–215. doi:10.1038/280214a0. Bibcode: 1979Natur.280..214G.
- ↑ Massi, Maria. "Accretion". http://www3.mpifr-bonn.mpg.de/staff/mmassi/lezione2WEdd.pdf.
- ↑ Weizsäcker, C. F. (1948). "Die Rotation Kosmischer Gasmassen" (in de). Zeitschrift für Naturforschung A 3 (8–11): 524–539. doi:10.1515/zna-1948-8-1118. Bibcode: 1948ZNatA...3..524W.
- ↑ 7.0 7.1 Shakura, N. I.; Sunyaev, R. A. (1973). "Black Holes in Binary Systems. Observational Appearance". Astronomy and Astrophysics 24: 337–355. Bibcode: 1973A&A....24..337S.
- ↑ Lynden-Bell, D.; Pringle, J. E. (1974). "The evolution of viscous discs and the origin of the nebular variables". Monthly Notices of the Royal Astronomical Society 168 (3): 603–637. doi:10.1093/mnras/168.3.603. Bibcode: 1974MNRAS.168..603L.
- ↑ 9.0 9.1 "A powerful local shear instability in weakly magnetized disks. I – Linear analysis". Astrophysical Journal 376: 214–233. 1991. doi:10.1086/170270. Bibcode: 1991ApJ...376..214B.
- ↑ Landau, L. D.; Lishitz, E. M. (1959). Fluid Mechanics. 6 (Reprint 1st ed.). Pergamon Press. ISBN 978-0-08-009104-4.
- ↑ Lightman, Alan P.; Eardley, Douglas M. (1974). "Black Holes in Binary Systems: Instability of Disk Accretion". The Astrophysical Journal 187: L1. doi:10.1086/181377. Bibcode: 1974ApJ...187L...1L.
- ↑ Piran, T. (1978). "The role of viscosity and cooling mechanisms in the stability of accretion disks". The Astrophysical Journal 221: 652. doi:10.1086/156069. Bibcode: 1978ApJ...221..652P.
- ↑ Poindexter, Shawn; Morgan, Nicholas; Kochanek, Christopher S. (2008). "The Spatial Structure of An Accretion Disk". The Astrophysical Journal 673 (1): 34–38. doi:10.1086/524190. Bibcode: 2008ApJ...673...34P.
- ↑ Eigenbrod, A.; Courbin, F.; Meylan, G.; Agol, E.; Anguita, T.; Schmidt, R. W.; Wambsganss, J. (2008). "Microlensing variability in the gravitationally lensed quasar QSO 2237+0305=the Einstein Cross. II. Energy profile of the accretion disk". Astronomy & Astrophysics 490 (3): 933–943. doi:10.1051/0004-6361:200810729. Bibcode: 2008A&A...490..933E.
- ↑ Mosquera, A. M.; Muñoz, J. A.; Mediavilla, E. (2009). "Detection of chromatic microlensing in Q 2237+0305 A". The Astrophysical Journal 691 (2): 1292–1299. doi:10.1088/0004-637X/691/2/1292. Bibcode: 2009ApJ...691.1292M.
- ↑ Floyd, David J. E.; Bate, N. F.; Webster, R. L. (2009). "The accretion disc in the quasar SDSS J0924+0219". Monthly Notices of the Royal Astronomical Society 398 (1): 233–239. doi:10.1111/j.1365-2966.2009.15045.x. Bibcode: 2009MNRAS.398..233F.
- ↑ Balbus, Steven A. (2003), "Enhanced Angular Momentum Transport in Accretion Disks", Annu. Rev. Astron. Astrophys. 41 (1): 555–597, doi:10.1146/annurev.astro.41.081401.155207, Bibcode: 2003ARA&A..41..555B, https://cds.cern.ch/record/620708, retrieved 2018-09-02
- ↑ Rüdiger, Günther; Hollerbach, Rainer (2004), The Magnetic Universe: Geophysical and Astrophysical Dynamo Theory, Wiley-VCH, ISBN 978-3-527-40409-4, https://archive.org/details/magneticuniverse0000rudi[page needed]
- ↑ Blandford, Roger; Payne, David (1982). "Hydromagnetic flows from accretion discs and the production of radio jets". Monthly Notices of the Royal Astronomical Society 199 (4): 883–903. doi:10.1093/mnras/199.4.883. Bibcode: 1982MNRAS.199..883B.
- ↑ Beckwith, Kris; Hawley, John F.; Krolik, Julian H. (2009). "Transport of large-scale poloidal flux in black hole accretion". Astrophysical Journal 707 (1): 428–445. doi:10.1088/0004-637x/707/1/428. Bibcode: 2009ApJ...707..428B.
- ↑ Park, Seok Jae; Vishniac, Ethan (1996). "The Variability of Active Galactic Nuclei and the Radial Transport of Vertical Magnetic Flux". Astrophysical Journal 471: 158–163. doi:10.1086/177959. Bibcode: 1996ApJ...471..158P.
- ↑ Guan, Xiaoyue; Gammie, Charles F. (2009). "The turbulent magnetic Prandtl number of MHD turbulence in disks". Astrophysical Journal 697 (2): 1901–1906. doi:10.1088/0004-637x/697/2/1901. Bibcode: 2009ApJ...697.1901G.
- ↑ Shakura, N. I.; Sunyaev, R. A (1973). "Black holes in binary systems. Observational appearance". Astronomy and Astrophysics 24: 337–355. Bibcode: 1973A&A....24..337S.
- ↑ Jafari, Amir; Vishniac, Ethan (2018). "Magnetic field transport in accretion disks". The Astrophysical Journal 854 (1): 2. doi:10.3847/1538-4357/aaa75b. Bibcode: 2018ApJ...854....2J.
- ↑ Page, D. N.; Thorne, K. S. (1974). "Disk-Accretion onto a Black Hole. Time-Averaged Structure of Accretion Disk". Astrophys. J. 191 (2): 499–506. doi:10.1086/152990. Bibcode: 1974ApJ...191..499P.
- ↑ Luminet, J. P. (1979). "Image of a spherical black hole with thin accretion disk". Astron. Astrophys. 75 (1–2): 228–235. Bibcode: 1979A&A....75..228L.
- ↑ Marck, J. A. (1996). "Short-cut method of solution of geodesic equations for Schwarzchild black hole". Class. Quantum Grav. 13 (3): 393–. doi:10.1088/0264-9381/13/3/007. Bibcode: 1996CQGra..13..393M.
- ↑ 28.0 28.1 Clavin, Whitney; Harrington, J.D. (12 August 2014). "NASA's NuSTAR Sees Rare Blurring of Black Hole Light". https://www.jpl.nasa.gov/news/nasas-nustar-sees-rare-blurring-of-black-hole-light.
- ↑ Poindexter, Shawn; Morgan, Nicholas; Kochanek, Christopher S (2011). "A binary merger origin for inflated hot Jupiter planets". Astronomy & Astrophysics 535: A50. doi:10.1051/0004-6361/201116907. Bibcode: 2011A&A...535A..50M.
- Frank, Juhan; Andrew King; Derek Raine (2002), Accretion power in astrophysics (Third ed.), Cambridge University Press, ISBN 978-0-521-62957-7
- Krolik, Julian H. (1999), Active Galactic Nuclei, Princeton University Press, ISBN 978-0-691-01151-6
External links
- Professor John F. Hawley homepage, University of Virginia (archived 2015)
- The Dynamical Structure of Nonradiative Black Hole Accretion Flows, John F. Hawley and Steven A. Balbus, 2002 March 19, The Astrophysical Journal, 573:738-748, 2002 July 10
- Accretion discs, Scholarpedia
- Merali, Zeeya (21 June 2006). "Magnetic fields snare black holes' food". New Scientist. https://www.newscientist.com/article/mg19025574-600-magnetic-fields-snare-black-holes-food/.
 |



