Birth process

Short description: Type of continuous process in probability theory

A birth process with birth rates [math]\displaystyle{ \lambda_0, \lambda_1, \lambda_2, ... }[/math].

In probability theory, a birth process or a pure birth process is a special case of a continuous-time Markov process and a generalisation of a Poisson process. It defines a continuous process which takes values in the natural numbers and can only increase by one (a "birth") or remain unchanged. This is a type of birth–death process with no deaths. The rate at which births occur is given by an exponential random variable whose parameter depends only on the current value of the process

Definition

Birth rates definition

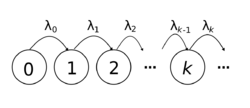
A birth process with birth rates [math]\displaystyle{ (\lambda_n, n\in \mathbb{N}) }[/math] and initial value [math]\displaystyle{ k\in \mathbb{N} }[/math] is a minimal right-continuous process [math]\displaystyle{ (X_t, t\ge 0) }[/math] such that [math]\displaystyle{ X_0=k }[/math] and the interarrival times [math]\displaystyle{ T_i = \inf\{t\ge 0: X_t=i+1\} - \inf\{t\ge 0: X_t=i\} }[/math] are independent exponential random variables with parameter [math]\displaystyle{ \lambda_i }[/math].

Infinitesimal definition

A birth process with rates [math]\displaystyle{ (\lambda_n, n\in \mathbb{N}) }[/math] and initial value [math]\displaystyle{ k\in \mathbb{N} }[/math] is a process [math]\displaystyle{ (X_t, t\ge 0) }[/math] such that:

• [math]\displaystyle{ X_0=k }[/math]
• [math]\displaystyle{ \forall s,t\ge 0: s\lt t\implies X_s \le X_t }[/math]
• [math]\displaystyle{ \mathbb{P}(X_{t+h}=X_t+1)=\lambda_{X_t}h+o(h) }[/math]
• [math]\displaystyle{ \mathbb{P}(X_{t+h}=X_t)=o(h) }[/math]
• [math]\displaystyle{ \forall s,t\ge 0: s\lt t\implies X_t-X_s }[/math] is independent of [math]\displaystyle{ (X_u, u \lt s) }[/math]

(The third and fourth conditions use little o notation.)

These conditions ensure that the process starts at [math]\displaystyle{ i }[/math], is non-decreasing and has independent single births continuously at rate [math]\displaystyle{ \lambda_n }[/math], when the process has value [math]\displaystyle{ n }[/math].

Continuous-time Markov chain definition

A birth process can be defined as a continuous-time Markov process (CTMC) [math]\displaystyle{ (X_t, t\ge 0) }[/math] with the non-zero Q-matrix entries [math]\displaystyle{ q_{n,n+1}=\lambda_n=-q_{n,n} }[/math] and initial distribution [math]\displaystyle{ i }[/math] (the random variable which takes value [math]\displaystyle{ i }[/math] with probability 1).

[math]\displaystyle{ Q=\begin{pmatrix} -\lambda_0 & \lambda_0 & 0 & 0 & \cdots \\ 0 & -\lambda_1 & \lambda_1 & 0 & \cdots \\ 0 & 0 & -\lambda_2 & \lambda_2 & \cdots\\ \vdots & \vdots & \vdots & & \vdots \ddots \end{pmatrix} }[/math]

Variations

Some authors require that a birth process start from 0 i.e. that [math]\displaystyle{ X_0=0 }[/math], while others allow the initial value to be given by a probability distribution on the natural numbers. The state space can include infinity, in the case of an explosive birth process. The birth rates are also called intensities.

Properties

As for CTMCs, a birth process has the Markov property. The CTMC definitions for communicating classes, irreducibility and so on apply to birth processes. By the conditions for recurrence and transience of a birth–death process, any birth process is transient. The transition matrices [math]\displaystyle{ ((p_{i,j}(t))_{i,j\in\mathbb{N}}), t\ge 0) }[/math] of a birth process satisfy the Kolmogorov forward and backward equations.

The backwards equations are:

[math]\displaystyle{ p'_{i,j}(t)=\lambda_i (p_{i+1,j}(t)-p_{i,j}(t)) }[/math] (for [math]\displaystyle{ i,j\in\mathbb{N} }[/math])

The forward equations are:

[math]\displaystyle{ p'_{i,i}(t)=-\lambda_i p_{i,i}(t) }[/math] (for [math]\displaystyle{ i\in\mathbb{N} }[/math])

[math]\displaystyle{ p'_{i,j}(t)=\lambda_{j-1}p_{i,j-1}(t)-\lambda_j p_{i,j}(t) }[/math] (for [math]\displaystyle{ j\ge i+1 }[/math])

From the forward equations it follows that:

[math]\displaystyle{ p_{i,i}(t)=e^{-\lambda_i t} }[/math] (for [math]\displaystyle{ i\in\mathbb{N} }[/math])

[math]\displaystyle{ p_{i,j}(t)=\lambda_{j-1}e^{-\lambda_j t}\int_0^t e^{\lambda_j s}p_{i,j-1}(s)\, \text{d} s }[/math] (for [math]\displaystyle{ j\ge i+1 }[/math])

Unlike a Poisson process, a birth process may have infinitely many births in a finite amount of time. We define [math]\displaystyle{ T_\infty=\sup \{T_n:n\in\mathbb{N}\} }[/math] and say that a birth process explodes if [math]\displaystyle{ T_\infty }[/math] is finite. If [math]\displaystyle{ \sum_{n=0}^\infty \frac{1}{\lambda_n}\lt \infty }[/math] then the process is explosive with probability 1; otherwise, it is non-explosive with probability 1 ("honest").

Examples

A Poisson process is a special case of a birth process.

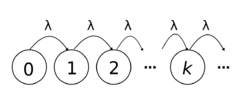
A Poisson process is a birth process where the birth rates are constant i.e. [math]\displaystyle{ \lambda_n=\lambda }[/math] for some [math]\displaystyle{ \lambda\gt 0 }[/math].

Simple birth process

A simple birth process, where birth rates are equal to the size of the current population.

A simple birth process is a birth process with rates [math]\displaystyle{ \lambda_n=n\lambda }[/math]. It models a population in which each individual gives birth repeatedly and independently at rate [math]\displaystyle{ \lambda }[/math]. Udny Yule studied the processes, so they may be known as Yule processes.

The number of births in time [math]\displaystyle{ t }[/math] from a simple birth process of population [math]\displaystyle{ n }[/math] is given by:

[math]\displaystyle{ p_{n,n+m}(t)=\binom{n}{m}(\lambda t)^m(1-\lambda t)^{n-m}+o(h) }[/math]

In exact form, the number of births is the negative binomial distribution with parameters [math]\displaystyle{ n }[/math] and [math]\displaystyle{ e^{-\lambda t} }[/math]. For the special case [math]\displaystyle{ n=1 }[/math], this is the geometric distribution with success rate [math]\displaystyle{ e^{-\lambda t} }[/math].

The expectation of the process grows exponentially; specifically, if [math]\displaystyle{ X_0=1 }[/math] then [math]\displaystyle{ \mathbb{E}(X_t)=e^{\lambda t} }[/math].

A simple birth process with immigration is a modification of this process with rates [math]\displaystyle{ \lambda_n=n\lambda+\nu }[/math]. This models a population with births by each population member in addition to a constant rate of immigration into the system.

References

• Grimmett, G. R.; Stirzaker, D. R. (1992). Probability and Random Processes (second ed.). Oxford University Press. ISBN 0198572220. 
• {{cite journal| url=https://www.ams.org/journals/tran/1957-086-02/S0002-9947-1957-0094854-8/S0002-9947-1957-0094854-8.pdf
• Norris, J.R. (1997). Markov Chains. Cambridge University Press. ISBN 9780511810633. 
• Ross, Sheldon M. (2010). Introduction to Probability Models (tenth ed.). Academic Press. ISBN 9780123756862. 
• Upton, G.; Cook, I. (2014). A Dictionary of Statistics (third ed.). ISBN 9780191758317.