Chemistry:ECW model

From HandWiki
Short description: Semi-quantitative model describing interactions between acids and bases of Lewis

In chemistry, the ECW model is a semi-quantitative model that describes and predicts the strength of Lewis acid–Lewis base interactions. Many chemical reactions can be described as acid–base reactions, so models for such interactions are of potentially broad interest. The model initially assigned E and C parameters to each and every acid and base. The model was later expanded to the ECW model to cover reactions that have a constant energy term, W, which describes processes that precede the acid–base reaction. This quantitative model is often discussed with the qualitative HSAB theory, which also seeks to rationalize the behavior of diverse acids and bases.

History of the problem

As early as 1938, G. N. Lewis pointed out that the relative strength of an acid or base depended upon the base or acid against which it was measured.[1] No single rank order of acid or base strength can predict the energetics of the cross reaction. Consider the following pair of acid–base reactions:.

4F-C6H4OH + OEt2   −ΔH = 5.94 kcal/mole
4F-C6H4OH + SMe2   −ΔH = 4.73 kcal/mole

These data suggest that OEt2 is a stronger base than SMe2. The opposite is found, however, when I2 is the acid:

I2 + OEt2   −ΔH = 4.16 kcal/mole
I2 + SMe2   −ΔH = 7.63 kcal/mole

E and C equation

The E-C model accommodates the failure of single parameter descriptions of acids and bases. In 1965 Russell S. Drago and Bradford Wayland published the two term equation such that each acid and each base is described by two parameters.[2] Each acid is characterized by an EA and a CA. Each base is likewise characterized by its own EB and CB. The E and C parameters refer, respectively, to the electrostatic and covalent contributions to the strength of the bonds that the acid and base will form. These parameters have been empirically obtained by using enthalpies for adducts that form only σ bonds between the acid and base as well as adducts that have no steric repulsion between the acid and base.

[math]\displaystyle{ -\Delta H= E_AE_B + C_AC_B }[/math]

This equation reproduces and predicts the enthalpy, ΔH, of a reaction between many acids and a bases. ΔH is a measure of strength of the bond between the acid and the base, both in the gas phase and in weakly solvating media. Entropy effects are ignored. A matrix presentation of the equation enhances its utility.[3]

Four values, two E and two C were assigned as references. EA and CA of I2 were chosen as standards. Since I2 has little tendency to undergo electrostatic bonding, the EA parameter was assigned a small value, 0.5, while the value of CA for the covalent property was set at 2.0. For the two base parameters, EB for CH3C(O)N(CH3)2 (DMA) was set at 2.35 and CB for (C2H5)2S, diethyl sulfide, was set at 3.92. Fixing the parameters in this way imposed the covalent-electrostatic model on the data set by fixing the EAEB and CACB products of the DMA and (C2H5)2S adducts with iodine, and these four values ensured that none of the parameters had negative values. Due to increasing enthalpy data that became available since the EC equation was first proposed the parameters have been improved. Mixing E and C numbers from the improved set of parameters with older parameters will result in incorrect calculations and is to be avoided.[4] A select set of the improved E and C numbers is found in this article and the complete set is available in the literature.[5] [6] EB and CB parameters for phosphines that can be used in combination with the improved parameters for oxygen, nitrogen, and sulfur donors to measure σ-basicity have been reported.[7]

ECW model

In the ECW model, a new term W was added to the equation.

[math]\displaystyle{ -\Delta H = E_AE_B + C_AC_B + W }[/math]

The W term represents a constant energy for cleavage of a dimeric acid or base. For example, the enthalpy of cleavage the [Rh(CO)2Cl]2 by base B involves two steps. The first step is cleavage of the dimer, which is W:

1/2 [Rh(CO)2Cl]2 → Rh(CO)2Cl   W = −10.39 kcal/mol

The second step is the binding of B to RhCl(CO)2 monomer. In this case, W = −10.39 kcal/mol.

In other cases, W is the enthalpy needed to cleave the internal hydrogen bonding of the H-bonding acid (CF3)3COH. W is also useful for a base displacement reaction in poorly solvating media:

F3B-OEt2 → BF3 + OEt2

For any base, a constant energy contribution is observed for the breaking of the F3B-OEt2 bond. An ECW study of the enthalpies of a series of bases produces a W value that corresponds to the enthalpy of dissociation of the F3B-OEt2 bond. The EA and CA parameters that result are those for uncomplexed BF3.

A graphical presentation of the ECW model

A graphical presentation of this model clearly shows that there is no single rank order of acid or base strength, a point often overlooked, and emphasizes that the magnitude of acid and base interactions requires two parameters (E & C) to account for the interactions.[8]

The EC equation from the ECW Model

[math]\displaystyle{ -\Delta H= E_AE_B + C_AC_B }[/math]

can be rearranged into a form which can be plotted as a straight line.

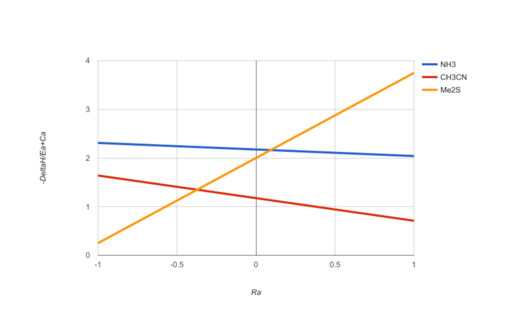
C-B plot using only three Lewis bases to show this graphical approach.

In a Cramer–Bopp plot for Lewis bases, the parameter Ra[lower-alpha 1] reflects the mode of bonding of a potential Lewis acid partner, from purely electrostatic interactions (Ra = −1) to purely covalent interactions (Ra = +1). The parameter [math]\displaystyle{ \scriptstyle\frac{-\Delta H}{E_a + C_a} }[/math] reflects the strength of the bonding interaction. The plot shown here allows comparison of three chosen Lewis bases: acetonitrile, ammonia, and dimethyl sulfide. The Lewis acid iodine (Ra = 0.6) will interact most strongly with dimethyl sulfide and least strongly with acetonitrile, whereas triethylgallium (Ra = −0.65) will interact most strongly with ammonia and least strongly with dimethyl sulfide. The plot also shows that ammonia is a stronger Lewis base than acetonitrile irrespective of its Lewis acid partner, whereas the relative strengths of ammonia and dimethyl sulfide as Lewis bases depends on the bonding characteristics of the Lewis acid, swapping order when Ra = 0.1. (NB: guesstimate).[clarification needed] The Cramer–Bopp plot was developed as a visual tool for comparing Lewis base strength with the range of possible Lewis acid partners, and a similar plot can be constructed to examine selected Lewis acids against the range of possible Lewis bases. References 5, 8, 12, and 14 contain graphical presentations that define the ranking order of strength of many Lewis acids and bases.

Other aspects and extensions of the ECW model

As mentioned above the E and C parameters are obtained from enthalpies of adduct formation in which the bond between the acid and base is a σ interaction and adducts that have no steric repulsion between the acid and base. As a result, E and C parameters can be used to glean information about pi bonding. When pi bonding contributes to the measured enthalpy, the enthalpy calculated from the E and C parameters will be less than the measured enthalpy and the difference provides a measure of the extent of the pi bonding contribution.[9][10]

The ᐃH calculated for the reaction of Me3B with Me3N is larger than the observed. This discrepancy is attributed to steric repulsion between the methyl groups on the B and N. The difference between the calculated and observed values can then be taken as the amount of the steric effect, a value otherwise not attainable. Steric effects have also been identified with (CH3)3SnCl and with Cu(HFacac)2.

The use of E and C parameters have been extended to analyze spectroscopic changes occurring during adduct formation.[11] For example, the shift of the phenol OH stretching frequency, Δχ, that occurs upon adduct formation has been analyzed using the following equation:

Δχ = ΕA∗EB + CA∗CB + W∗

where asterisks on the EA and CA for phenol indicate that the acceptor is held constant and the frequency shift is measured as the base is varied. The asterisks also indicate that the phenol parameters are those for frequency shifts and not those for enthalpies. An analysis like this provides a basis for using EB and CB parameters as a reference scale of donor strengths for frequency shifts. This type analysis has also been applied to other spectroscopic shifts (NMR, EPR, UV-vis, IR, etc.) accompanying adduct formation. Any physicochemical property, Δχ, that is dominated by σ donor-acceptor interaction can be correlated with the enthalpy-derived E and C parameters.

The ECW equations enables one to correlate and predict the enthalpies of adduct formation of neutral donor-acceptor interactions for which the electron-transfer is limited. For gas-phase reactions between cations and neutral donors, there is significant electron-transfer. The extension of the ECW model to cation-neutral Lewis base interactions has led to the ECT model.[12][13] Others have concluded that the ECW model "is generally found helpful in many fields of solution chemistry and biochemistry".[14]

Selected E and C parameters for acids[lower-alpha 2]
Acid EA CA W CA/EA
I2 0.50 2.0 0 4.0
IBr 1.20 3.29 0 2.7
ICl 2.92 1.66 0 0.57
C6H5OH 2.27 1.07 0 0.47
4-FC6H4OH 2.30 1.11 0 0.48
3-CF3C6H4OH 2.38 1.22 0 0.51
4-CH3C6H4OH 2.23 1.03 0 0.44
CF3CH2OH 2.07 1.06 0 0.51
(CF3)2CHOH 2.89 1.33 −0.16 0.46
(CH3)3COH 1.07 0.69 0 0.65
(CF3)3COH 3.06 1.88 −0.87 0.61
C8H17OH 0.85 0.87 0 1.0
HCCl3 1.56 0.44 0 0.28
CH2Cl2 0.86 0.11 0 0.13
C4H4NH 1.38 0.68 0 0.49
HNCO 1.60 0.69 0 0.43
HNCS 2.85 0.70 0 0.25
B(CH3)3 2.90 3.60 0 1.2
Al(CH3)3 8.66 3.68 0 0.43
Ga(C2H5)3 6.95 1.48 0 0.21
In(CH3)3 6.60 2.15 0 0.33
(CH3)3SnCl 2.87 0.71 0 0.25
SO2 0.51 1.56 0 3.1
SbCl5 3.64 10.42 0 2.9
Cu(HFacac)2[lower-alpha 3] 1.82 2.86 0 1.6
Zn[N(Si(CH3)3]2 2.75 2.32 0 0.84
Cd[N(Si(CH3)3]2 2.50 1.83 0 0.73
ZnTPP[lower-alpha 4] 2.72 1.45 0 0.53
CoPPIXDME[lower-alpha 5] 2.32 1.34 0 0.58
½[MeCo(Hdmg)2]2[lower-alpha 6] 4.70 3.24 −5.84 0.60
½[Rh(CO)2Cl]2 4.32 4.13 −10.39 0.96
½[Rh(COD)2Cl]2 2.43 2.56 −5.78 1.1
½[Pd(π-ally)Cl]2 1.70 2.14 −3.38 1.3
[Ni(TFAcCAM)2]2[lower-alpha 7] 1.55 1.32 0 0.85
Mo2PFB4[lower-alpha 8] 3.15 1.05 0 0.33
and for bases[lower-alpha 9]
Base EB CB CB/EB
NH3 2.31 2.04 0.88
NH2(CH3) 2.16 3.13 1.4
NH(CH3)2 1.80 4.21 2.3
N(CH3)3 1.21 5.61 4.6
HC(C2H4)3N 0.80 6.72 8.4
(C2H5)3N 1.32 5.73 4.3
1-CH3NC3N[lower-alpha 10] 1.16 4.92 4.2
C5H5N 1.78 3.54 2.0
3CH3C5H4N 1.81 3.67 2.0
3BrC5H4N 1.66 3.08 1.9
4CH3OC5H4N 1.83 3.83 2.1
CH3CN 1.64 0.71 0.43
(CH3)2NCN 1.92 0.92 0.48
ClCH2CN 1.67 0.33 0.20
CH3C(O)CH3 1.74 1.26 0.72
(CH2)4CO 2.02 0.88 0.43
CH3C(O)OC2H5 1.62 0.98 0.61
CH3C(O)N(CH3)2 2.35 1.31 0.56
(C2H5)2O 1.80 1.63 0.91
(CH2)4O 1.64 2.18 1.3
O(C2H4)2)O 1.86 1.29 0.69
(CH2)4(CH)2)O[lower-alpha 11] 1.45 2.14 1.5
(CH3)2S 0.25 3.75 15
(CH2)4S 0.26 4.07 16
(C2H5)2S 0.24 3.92 16
(CH3)2SO 2.40 1.47 0.61
(CH2)4SO 2.44 1.64 0.67
C5H5NO 2.29 2.33 1.0
4CH3OC5N4NO 2.34 3.02 1,3
(C6H5)3PO 2.59 1.67 0.64
(CH3)3P 0.25 5.81 24
(CH3O)3P 0.13 4.83 37
(CH3)2Se 0.05 4.24 83
(C6H5)3PS 0.35 3.65 10
C6H6 0.70 0.45 0.64

Charge-transfer complexes of I2

The enthalpies of formation of some Donor-I2 adducts are listed below. I2 is a Lewis acid classified as a soft acid and its acceptor properties are discussed in the ECW model. The relative acceptor strength of I2 toward a series of bases, versus other Lewis acids, can be illustrated by C-B plots.[15]

Enthalpies of formation of some donor-I2 adducts
Base −ΔH (kcal/mol)
Benzene 1.4
Toluene 1.8
Dioxane 3.5
Diethyl ether 4.3
Diethyl sulfide 8.3
Dimethylacetamide 4.7
Acetonitrile 1.9
Pyridine 7.80
Triethylamine 12.0

Notes

  1. ↑ (CA − EA)/(CA + EA)
  2. ↑ units for EA, and CA are (kcal/mol)​1⁄2 and W is kcal/mol
  3. ↑ bis(hexafloroacetylacetonato)copper(II)
  4. ↑ zinc tetraphenylporphine
  5. ↑ cobalt(II) protoporhyrin IX dimethyl ester IX
  6. ↑ methylcobaloxime
  7. ↑ bis(3-trifluoro-d-camphorate)nickel(II) dimer
  8. ↑ molybdenum perfluorobutyrate
  9. ↑ Units for EB and CB are (kcal/mol)​1⁄2
  10. ↑ N-methylimidazole
  11. ↑ 7-Oxabicyclo[2.2.1]heptane

References

  1. ↑ Lewis G. N. (1938) Acids and bases Journal of the Franklin Institute, 226, 293-313.
  2. ↑ Drago, R. S.; Wayland, B. B. (1965). "A Double-Scale Equation for Correlating Enthalpies of Lewis Acid-Base Interactions". Journal of the American Chemical Society 87 (16): 3571–3577. doi:10.1021/ja01094a008. 
  3. ↑ Drago, R. S.; Vogel,G. C.; Needham, T. E. (1971). "A Four-Parameter Equation for Predicting Enthalpies of Adduct Formation". Journal of the American Chemical Society 93 (23): 6014–6026. doi:10.1021/ja00752a010. 
  4. ↑ Drago, R. S.; Ferris, D. C..P.; Wong, N..M. (1990). "A method for the analysis and prediction of gas-phase ion-molecule enthalpies". Journal of the American Chemical Society 112 (24): 8953–8961–2479. doi:10.1021/ja00180a047. 
  5. ↑ Vogel G. C.; Drago, R. S. (1996). "The ECW Model". Journal of Chemical Education 73 (8): 701–707. doi:10.1021/ed073p701. Bibcode: 1996JChEd..73..701V. 
  6. ↑ Drago, R. S.; Dadmun, A. P.; Vogel, G. C. (1992). "Addition of new donors to the E and C model.". Inorganic Chemistry 32 (11): 2473–2479. doi:10.1021/ic00063a045. 
  7. ↑ Drago, R. S.; Joerg,S. (1996). "Phosphine EB and CB Values". Journal of the American Chemical Society 118 (11): 2654–2663. doi:10.1021/ja953581e. 
  8. ↑ Cramer, R. E.; Bopp, T. T. (1977). "Graphical display of the enthalpies of adduct formation for Lewis acids and bases". Journal of Chemical Education 54: 612–613. doi:10.1021/ed054p612.  The plots shown in this paper used older parameters. Improved E&C parameters are listed in the tables and in references 5 and 6.
  9. ↑ Drago, R. S.; Bilgrien, C. J. (1988). "Inductive transfer and coordination of ligands in metal-metal bonded systems". Polyhedron 7 (16–17): 1453–1468. doi:10.1016/S0277-5387(00)81774-X. 
  10. ↑ Drago, R. S. (1982). "The question of a synergistic metal-metal interaction leading to .pi.-back-bond stabilization in dirhodium tetrabutyrate adducts". Inorg. Chem. 21 (4): 1697–1698. doi:10.1021/ic00134a093. 
  11. ↑ Drago, R. S.; Vogel, G. C. (1992). "Interpretation of spectroscopic changes upon adduct formation and their use to determine electrostatic and covalent (E and C) parameters". Journal of the American Chemical Society 114 (24): 9527–9532. doi:10.1021/ja00050a035. 
  12. ↑ Drago, R. S. Applications of Electrostatic-Covalent Models in Chemistry, Surfside: Gainesville, FL, 1994.
  13. ↑ Drago, R.; Wong, N. S. (1996). "The Role of Electron-Density Transfer and Electronegativity in Understanding Chemical Reactivity and Bonding". Journal of Chemical Education 73 (2): 123–129. doi:10.1021/ed073p123. Bibcode: 1996JChEd..73..123D. 
  14. ↑ Laurence, C. and Gal, J-F. Lewis Basicity and Affinity Scales, Data and Measurement, (Wiley 2010) p 51 ISBN 978-0-470-74957-9
  15. ↑ Laurence, C. and Gal, J-F. Lewis Basicity and Affinity Scales, Data and Measurement, (Wiley 2010) pp 50-51 ISBN 978-0-470-74957-9

See also



Retrieved from "https://handwiki.org/wiki/index.php?title=Chemistry:ECW_model&oldid=3324144"