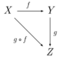Fibred category
Fibred categories (or fibered categories) are abstract entities in mathematics used to provide a general framework for descent theory. They formalise the various situations in geometry and algebra in which inverse images (or pull-backs) of objects such as vector bundles can be defined. As an example, for each topological space there is the category of vector bundles on the space, and for every continuous map from a topological space X to another topological space Y is associated the pullback functor taking bundles on Y to bundles on X. Fibred categories formalise the system consisting of these categories and inverse image functors. Similar setups appear in various guises in mathematics, in particular in algebraic geometry, which is the context in which fibred categories originally appeared. Fibered categories are used to define stacks, which are fibered categories (over a site) with "descent". Fibrations also play an important role in categorical semantics of type theory, and in particular that of dependent type theories.
Fibred categories were introduced by Alexander Grothendieck (1959, 1971), and developed in more detail by Jean Giraud (1964, 1971).
Background and motivations
There are many examples in topology and geometry where some types of objects are considered to exist on or above or over some underlying base space. The classical examples include vector bundles, principal bundles, and sheaves over topological spaces. Another example is given by "families" of algebraic varieties parametrised by another variety. Typical to these situations is that to a suitable type of a map between base spaces, there is a corresponding inverse image (also called pull-back) operation taking the considered objects defined on to the same type of objects on . This is indeed the case in the examples above: for example, the inverse image of a vector bundle on is a vector bundle on .
Moreover, it is often the case that the considered "objects on a base space" form a category, or in other words have maps (morphisms) between them. In such cases the inverse image operation is often compatible with composition of these maps between objects, or in more technical terms is a functor. Again, this is the case in examples listed above.
However, it is often the case that if is another map, the inverse image functors are not strictly compatible with composed maps: if is an object over (a vector bundle, say), it may well be that
Instead, these inverse images are only naturally isomorphic. This introduction of some "slack" in the system of inverse images causes some delicate issues to appear, and it is this set-up that fibred categories formalise.
The main application of fibred categories is in descent theory, concerned with a vast generalisation of "glueing" techniques used in topology. In order to support descent theory of sufficient generality to be applied in non-trivial situations in algebraic geometry the definition of fibred categories is quite general and abstract. However, the underlying intuition is quite straightforward when keeping in mind the basic examples discussed above.
Formal definitions
There are two essentially equivalent technical definitions of fibred categories, both of which will be described below. All discussion in this section ignores the set-theoretical issues related to "large" categories. The discussion can be made completely rigorous by, for example, restricting attention to small categories or by using universes.
Cartesian morphisms and functor
If is a functor between two categories and is an object of , then the subcategory of consisting of those objects for which and those morphisms satisfying , is called the fibre category (or fibre) over , and is denoted . The morphisms of are called -morphisms, and for objects of , the set of -morphisms is denoted by . The image by of an object or a morphism in is called its projection (by ). If is a morphism of , then those morphisms of that project to are called -morphisms, and the set of -morphisms between objects and in is denoted by .
A morphism in is called -cartesian (or simply cartesian) if it satisfies the following condition:
- if is the projection of , and if is an -morphism, then there is precisely one -morphism such that .
A cartesian morphism is called an inverse image of its projection ; the object is called an inverse image of by .
The cartesian morphisms of a fibre category are precisely the isomorphisms of . There can in general be more than one cartesian morphism projecting to a given morphism , possibly having different sources; thus there can be more than one inverse image of a given object in by . However, it is a direct consequence of the definition that two such inverse images are isomorphic in .
A functor is also called an -category, or said to make into an -category or a category over . An -functor from an -category to an -category is a functor such that . -categories form in a natural manner a 2-category, with 1-morphisms being -functors, and 2-morphisms being natural transformations between -functors whose components lie in some fibre.
An -functor between two -categories is called a cartesian functor if it takes cartesian morphisms to cartesian morphisms. Cartesian functors between two -categories form a category , with natural transformations as morphisms. A special case is provided by considering as an -category via the identity functor: then a cartesian functor from to an -category is called a cartesian section. Thus a cartesian section consists of a choice of one object in for each object in , and for each morphism a choice of an inverse image . A cartesian section is thus a (strictly) compatible system of inverse images over objects of . The category of cartesian sections of is denoted by
In the important case where has a terminal object (thus in particular when is a topos or the category of arrows with target in ) the functor
is fully faithful (Lemma 5.7 of Giraud (1964)).
Fibred categories and cloven categories
The technically most flexible and economical definition of fibred categories is based on the concept of cartesian morphisms. It is equivalent to a definition in terms of cleavages, the latter definition being actually the original one presented in Grothendieck (1959); the definition in terms of cartesian morphisms was introduced in Grothendieck (1971) in 1960–1961.
An category is a fibred category (or a fibred -category, or a category fibred over ) if each morphism of whose codomain is in the range of projection has at least one inverse image, and moreover the composition of any two cartesian morphisms in is always cartesian. In other words, an -category is a fibred category if inverse images always exist (for morphisms whose codomains are in the range of projection) and are transitive.
If has a terminal object and if is fibred over , then the functor from cartesian sections to defined at the end of the previous section is an equivalence of categories and moreover surjective on objects.
If is a fibred -category, it is always possible, for each morphism in and each object in , to choose (by using the axiom of choice) precisely one inverse image . The class of morphisms thus selected is called a cleavage and the selected morphisms are called the transport morphisms (of the cleavage). A fibred category together with a cleavage is called a cloven category. A cleavage is called normalised if the transport morphisms include all identities in ; this means that the inverse images of identity morphisms are chosen to be identity morphisms. Evidently if a cleavage exists, it can be chosen to be normalised; we shall consider only normalised cleavages below.
The choice of a (normalised) cleavage for a fibred -category specifies, for each morphism in , a functor ; on objects is simply the inverse image by the corresponding transport morphism, and on morphisms it is defined in a natural manner by the defining universal property of cartesian morphisms. The operation which associates to an object of the fibre category and to a morphism the inverse image functor is almost a contravariant functor from to the category of categories. However, in general it fails to commute strictly with composition of morphisms. Instead, if and are morphisms in , then there is an isomorphism of functors
These isomorphisms satisfy the following two compatibilities:
- for three consecutive morphisms and object the following holds:
It can be shown (see Grothendieck (1971) section 8) that, inversely, any collection of functors together with isomorphisms satisfying the compatibilities above, defines a cloven category. These collections of inverse image functors provide a more intuitive view on fibred categories; and indeed, it was in terms of such compatible inverse image functors that fibred categories were introduced in Grothendieck (1959).
The paper by Gray referred to below makes analogies between these ideas and the notion of fibration of spaces.
These ideas simplify in the case of groupoids, as shown in the paper of Brown referred to below, which obtains a useful family of exact sequences from a fibration of groupoids.
Splittings and split fibred categories
A (normalised) cleavage such that the composition of two transport morphisms is always a transport morphism is called a splitting, and a fibred category with a splitting is called a split (fibred) category. In terms of inverse image functors the condition of being a splitting means that the composition of inverse image functors corresponding to composable morphisms in equals the inverse image functor corresponding to . In other words, the compatibility isomorphisms of the previous section are all identities for a split category. Thus split -categories correspond exactly to true functors from to the category of categories.
Unlike cleavages, not all fibred categories admit splittings. For an example, see below.
Co-cartesian morphisms and co-fibred categories
One can invert the direction of arrows in the definitions above to arrive at corresponding concepts of co-cartesian morphisms, co-fibred categories and split co-fibred categories (or co-split categories). More precisely, if is a functor, then a morphism in is called co-cartesian if it is cartesian for the opposite functor . Then is also called a direct image and a direct image of for . A co-fibred -category is an -category such that direct image exists for each morphism in and that the composition of direct images is a direct image. A co-cleavage and a co-splitting are defined similarly, corresponding to direct image functors instead of inverse image functors.
Properties
The 2-categories of fibred categories and split categories
The categories fibred over a fixed category form a 2-category , where the category of morphisms between two fibred categories and is defined to be the category of cartesian functors from to .
Similarly the split categories over form a 2-category (from French catégorie scindée), where the category of morphisms between two split categories and is the full sub-category of -functors from to consisting of those functors that transform each transport morphism of into a transport morphism of . Each such morphism of split -categories is also a morphism of -fibred categories, i.e., .
There is a natural forgetful 2-functor that simply forgets the splitting.
Existence of equivalent split categories
While not all fibred categories admit a splitting, each fibred category is in fact equivalent to a split category. Indeed, there are two canonical ways to construct an equivalent split category for a given fibred category over . More precisely, the forgetful 2-functor admits a right 2-adjoint and a left 2-adjoint (Theorems 2.4.2 and 2.4.4 of Giraud 1971), and and are the two associated split categories. The adjunction functors and are both cartesian and equivalences (ibid.). However, while their composition is an equivalence (of categories, and indeed of fibred categories), it is not in general a morphism of split categories. Thus the two constructions differ in general. The two preceding constructions of split categories are used in a critical way in the construction of the stack associated to a fibred category (and in particular stack associated to a pre-stack).
Categories fibered in groupoids
There is a related construction to fibered categories called categories fibered in groupoids. These are fibered categories such that any subcategory of given by
- Fix an object
- The objects of the subcategory are where
- The arrows are given by such that
is a groupoid denoted . The associated 2-functors from the Grothendieck construction are examples of stacks. In short, the associated functor sends an object to the category , and a morphism induces a functor from the fibered category structure. Namely, for an object considered as an object of , there is an object where . This association gives a functor which is a functor of groupoids.
Examples
Fibered categories
- The functor , sending a category to its set of objects, is a fibration. For a set , the fiber consists of categories with . The cartesian arrows are the fully faithful functors.
- Categories of arrows: For any category the category of arrows in has as objects the morphisms in , and as morphisms the commutative squares in (more precisely, a morphism from to consists of morphisms and such that ). The functor which takes an arrow to its target makes into an -category; for an object of the fibre is the category of -objects in , i.e., arrows in with target . Cartesian morphisms in are precisely the cartesian squares in , and thus is fibred over precisely when fibre products exist in .
- Fibre bundles: Fibre products exist in the category of topological spaces and thus by the previous example is fibred over . If is the full subcategory of consisting of arrows that are projection maps of fibre bundles, then is the category of fibre bundles on and is fibred over . A choice of a cleavage amounts to a choice of ordinary inverse image (or pull-back) functors for fibre bundles.
- Vector bundles: In a manner similar to the previous examples the projections of real (complex) vector bundles to their base spaces form a category () over (morphisms of vector bundles respecting the vector space structure of the fibres). This -category is also fibred, and the inverse image functors are the ordinary pull-back functors for vector bundles. These fibred categories are (non-full) subcategories of .
- Sheaves on topological spaces: The inverse image functors of sheaves make the categories of sheaves on topological spaces into a (cleaved) fibred category over . This fibred category can be described as the full sub-category of consisting of étalé spaces of sheaves. As with vector bundles, the sheaves of groups and rings also form fibred categories of .
- Sheaves on topoi: If is a topos and is an object in , the category of -objects is also a topos, interpreted as the category of sheaves on . If is a morphism in , the inverse image functor can be described as follows: for a sheaf on and an object in one has equals . These inverse image make the categories into a split fibred category on . This can be applied in particular to the "large" topos of topological spaces.
- Quasi-coherent sheaves on schemes: Quasi-coherent sheaves form a fibred category over the category of schemes. This is one of the motivating examples for the definition of fibred categories.
- Fibred category admitting no splitting: A group can be considered as a category with one object and the elements of as the morphisms, composition of morphisms being given by the group law. A group homomorphism can then be considered as a functor, which makes into a -category. It can be checked that in this set-up all morphisms in are cartesian; hence is fibred over precisely when is surjective. A splitting in this setup is a (set-theoretic) section of which commutes strictly with composition, or in other words a section of which is also a homomorphism. But as is well known in group theory, this is not always possible (one can take the projection in a non-split group extension).
- Co-fibred category of sheaves: The direct image functor of sheaves makes the categories of sheaves on topological spaces into a co-fibred category. The transitivity of the direct image shows that this is even naturally co-split.
Category fibered in groupoids
One of the main examples of categories fibered in groupoids comes from groupoid objects internal to a category . So given a groupoid object
there is an associated groupoid object
in the category of contravariant functors from the yoneda embedding. Since this diagram applied to an object gives a groupoid internal to sets
there is an associated small groupoid . This gives a contravariant 2-functor , and using the Grothendieck construction, this gives a category fibered in groupoids over . Note the fiber category over an object is just the associated groupoid from the original groupoid in sets.
Group quotient
Given a group object acting on an object from , there is an associated groupoid object
where is the projection on and is the composition map . This groupoid gives an induced category fibered in groupoids denoted .
Two-term chain complex
For an abelian category any two-term complex
has an associated groupoid
where
this groupoid can then be used to construct a category fibered in groupoids. One notable example of this is in the study of the cotangent complex for local-complete intersections and in the study of exalcomm.
See also
References
- Giraud, Jean (1964). "Méthode de la descente". Mémoires de la Société Mathématique de France 2: viii+150.
- Giraud, Jean (1971). Cohomologie non abélienne. Springer. ISBN 3-540-05307-7.
- Grothendieck, Alexander (1959). "Technique de descente et théorèmes d'existence en géométrie algébrique. I. Généralités. Descente par morphismes fidèlement plats". Séminaire Bourbaki 5 (Exposé 190): viii+150.
- Gray, John W. (1966). "Fibred and cofibred categories". Springer. pp. 21–83. doi:10.1007/978-3-642-99902-4_2. ISBN 978-3-642-99902-4.
- Brown, R. (1970). "Fibrations of groupoids". J. Algebra 15: 103–132. doi:10.1016/0021-8693(70)90089-X. http://www.groupoids.org.uk/pdffiles/fibrationsgpds.pdf.
- Grothendieck, Alexander (2006). "Catégories fibrées et descente". 224. Springer. pp. 145–194. doi:10.1007/BFb0058662. ISBN 978-3-540-36910-3. Bibcode: 2002math......6203G.
- Bénabou, Jean (1985). "Fibered categories and the foundations of naive category theory". Journal of Symbolic Logic 50 (1): 10–37. doi:10.2307/2273784. http://projecteuclid.org/euclid.jsl/1183741771.
- Jacobs, Bart (1999). Categorical Logic and Type Theory. Studies in Logic and the Foundations of Mathematics 141. North Holland, Elsevier. ISBN 0-444-50170-3. https://www.cs.ru.nl/B.Jacobs/CLT/bookinfo.html.
- Vistoli, Angelo (2007), Notes on Grothendieck topologies, fibered categories and descent theory.
- Phoa, Wesley (1992). An introduction to fibrations, topos theory, the effective topos and modest sets (Technical report). LFCS, Department of Computer Science, University of Edinburgh. CiteSeerX 10.1.1.112.4533. ECS-LFCS-92-208.
- Brown, R.; Sivera, R. (2009). "Algebraic colimit calculations in homotopy theory using fibred and cofibred categories". Theory and Applications of Categories 22: 222–251. http://www.tac.mta.ca/tac/volumes/22/8/22-08abs.html.
- Brown, R.; Higgins, P.J.; Sivera, R. (2011). Nonabelian Algebraic Topology: filtered spaces, crossed complexes, cubical omega-groupoids. Tracts in Mathematics. 15. European Mathematical Society. ISBN 978-3-03719-083-8. http://groupoids.org.uk/nonab-a-t.html.
External links
- SGA 1.VI - Fibered categories and descent - pages 119-153
- Grothendieck fibration in nLab
 |