Axiom of choice
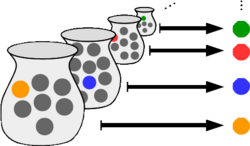

In mathematics, the axiom of choice, abbreviated AC or AoC, is an axiom of set theory equivalent to the statement that a Cartesian product of a collection of non-empty sets is non-empty. Informally put, the axiom of choice says that given any collection of sets, each containing at least one element, it is possible to construct a new set by choosing one element from each set, even if the collection is infinite. Formally, it states that for every indexed family of nonempty sets, there exists an indexed set such that for every . The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem.[1]
In many cases, a set created by choosing elements can be made without invoking the axiom of choice; this is, in particular, if the number of sets from which to choose the elements is finite, or if a canonical rule on how to choose the elements is available – some distinguishing property that happens to hold for exactly one element in each set. An illustrative example is sets picked from the natural numbers. From such sets, one may always select the smallest number, e.g. given the sets {{4, 5, 6}, {10, 12}, {1, 400, 617, 8000}}, the set containing each smallest element is {4, 10, 1}. In this case, "select the smallest number" is a choice function. Even if infinitely many sets were collected from the natural numbers, it will always be possible to choose the smallest element from each set to produce a set. That is, the choice function provides the set of chosen elements. However, no definite choice function is known for the collection of all non-empty subsets of the real numbers. In that case, the axiom of choice must be invoked.
Bertrand Russell coined an analogy: for any (even infinite) collection of pairs of shoes, one can pick out the left shoe from each pair to obtain an appropriate collection (i.e. set) of shoes; this makes it possible to define a choice function directly. For an infinite collection of pairs of socks (assumed to have no distinguishing features), there is no obvious way to make a function that forms a set out of selecting one sock from each pair, without invoking the axiom of choice.[2]
Although originally controversial, the axiom of choice is now used without reservation by most mathematicians,[3] and it is included in the standard form of axiomatic set theory, Zermelo–Fraenkel set theory with the axiom of choice (ZFC). One motivation for this use is that a number of generally accepted mathematical results, such as Tychonoff's theorem, require the axiom of choice for their proofs. Contemporary set theorists also study axioms that are not compatible with the axiom of choice, such as the axiom of determinacy. The axiom of choice is avoided in some varieties of constructive mathematics, although there are varieties of constructive mathematics in which the axiom of choice is embraced.
Statement
A choice function (also called selector or selection) is a function f, defined on a collection X of nonempty sets, such that for every set A in X, f(A) is an element of A. With this concept, the axiom can be stated:
Axiom — For any set X of nonempty sets, there exists a choice function f that is defined on X and maps each set of X to an element of that set.
Formally, this may be expressed as follows:
Thus, the negation of the axiom may be expressed as the existence of a collection of nonempty sets which has no choice function. Formally, this may be derived making use of the logical equivalence of to .
Each choice function on a collection X of nonempty sets is an element of the Cartesian product of the sets in X. This is not the most general situation of a Cartesian product of a family of sets, where a given set can occur more than once as a factor; however, one can focus on elements of such a product that select the same element every time a given set appears as factor, and such elements correspond to an element of the Cartesian product of all distinct sets in the family. The axiom of choice asserts the existence of such elements; it is therefore equivalent to:
- Given any family of nonempty sets, their Cartesian product is a nonempty set.
Nomenclature
In this article and other discussions of the Axiom of Choice the following abbreviations are common:
- AC – the Axiom of Choice. More rarely, AoC is used.[4]
- ZF – Zermelo–Fraenkel set theory omitting the Axiom of Choice.
- ZFC – Zermelo–Fraenkel set theory, extended to include the Axiom of Choice.
Variants
There are many other equivalent statements of the axiom of choice. These are equivalent in the sense that, in the presence of other basic axioms of set theory, they imply the axiom of choice and are implied by it.
One variation avoids the use of choice functions by, in effect, replacing each choice function with its range:
- Given any set X of pairwise disjoint non-empty sets, there exists at least one set C that contains exactly one element in common with each of the sets in X.[5]
This guarantees for any partition of a set X the existence of a subset C of X containing exactly one element from each part of the partition.
Another equivalent axiom only considers collections X that are essentially powersets of other sets:
- For any set A, the power set of A (with the empty set removed) has a choice function.
Authors who use this formulation often speak of the choice function on A, but this is a slightly different notion of choice function. Its domain is the power set of A (with the empty set removed), and so makes sense for any set A, whereas with the definition used elsewhere in this article, the domain of a choice function on a collection of sets is that collection, and so only makes sense for sets of sets. With this alternate notion of choice function, the axiom of choice can be compactly stated as
- Every set has a choice function.[6]
which is equivalent to
- For any set A there is a function f such that for any non-empty subset B of A, f(B) lies in B.
The negation of the axiom can thus be expressed as:
- There is a set A such that for all functions f (on the set of non-empty subsets of A), there is a B such that f(B) does not lie in B.
Restriction to finite sets
The usual statement of the axiom of choice does not specify whether the collection of nonempty sets is finite or infinite, and thus implies that every finite collection of nonempty sets has a choice function. However, that particular case is a theorem of the Zermelo–Fraenkel set theory without the axiom of choice (ZF); it is easily proved by the principle of finite induction.[7] In the even simpler case of a collection of one set, a choice function just corresponds to an element, so this instance of the axiom of choice says that every nonempty set has an element; this holds trivially. The axiom of choice can be seen as asserting the generalization of this property, already evident for finite collections, to arbitrary collections.
Usage
Until the late 19th century, the axiom of choice was often used implicitly, although it had not yet been formally stated. For example, after having established that the set X contains only non-empty sets, a mathematician might have said "let F(s) be one of the members of s for all s in X" to define a function F. In general, it is impossible to prove that F exists without the axiom of choice, but this seems to have gone unnoticed until Zermelo.
Examples
The nature of the individual nonempty sets in the collection may make it possible to avoid the axiom of choice even for certain infinite collections. For example, suppose that each member of the collection X is a nonempty subset of the natural numbers. Every such subset has a smallest element, so to specify our choice function we can simply say that it maps each set to the least element of that set. This gives us a definite choice of an element from each set, and makes it unnecessary to add the axiom of choice to our axioms of set theory.
The difficulty appears when there is no natural choice of elements from each set. If we cannot make explicit choices, how do we know that our selection forms a legitimate set (as defined by the other ZF axioms of set theory)? For example, suppose that X is the set of all non-empty subsets of the real numbers. First we might try to proceed as if X were finite. If we try to choose an element from each set, then, because X is infinite, our choice procedure will never come to an end, and consequently, we shall never be able to produce a choice function for all of X. Next we might try specifying the least element from each set. But some subsets of the real numbers do not have least elements. For example, the open interval (0,1) does not have a least element: if x is in (0,1), then so is x/2, and x/2 is always strictly smaller than x. So this attempt also fails.
Additionally, consider for instance the unit circle S, and the action on S by a group G consisting of all rational rotations. Namely, these are rotations by angles which are rational multiples of π. Here G is countable while S is uncountable. Hence S breaks up into uncountably many orbits under G. Using the axiom of choice, we could pick a single point from each orbit, obtaining an uncountable subset X of S with the property that all of its translates by G are disjoint from X. The set of those translates partitions the circle into a countable collection of disjoint sets, which are all pairwise congruent. Since X is not measurable for any rotation-invariant countably additive finite measure on S, finding an algorithm to form a set from selecting a point in each orbit requires that one add the axiom of choice to our axioms of set theory. See non-measurable set for more details.
In classical arithmetic, the natural numbers are well-ordered: for every nonempty subset of the natural numbers, there is a unique least element under the natural ordering. In this way, one may specify a set from any given subset. One might say, "Even though the usual ordering of the real numbers does not work, it may be possible to find a different ordering of the real numbers which is a well-ordering. Then our choice function can choose the least element of every set under our unusual ordering." The problem then becomes that of constructing a well-ordering, which turns out to require the axiom of choice for its existence; every set can be well-ordered if and only if the axiom of choice holds.
Criticism and acceptance
A proof requiring the axiom of choice may establish the existence of an object without explicitly defining the object in the language of set theory. For example, while the axiom of choice implies that there is a well-ordering of the real numbers, there are models of set theory with the axiom of choice in which no individual well-ordering of the reals is definable. Similarly, although a subset of the real numbers that is not Lebesgue measurable can be proved to exist using the axiom of choice, it is consistent that no such set is definable.[8]
The axiom of choice proves the existence of these intangibles (objects that are proved to exist, but which cannot be explicitly constructed), which may conflict with some philosophical principles.[9] Because there is no canonical well-ordering of all sets, a construction that relies on a well-ordering may not produce a canonical result, even if a canonical result is desired (as is often the case in category theory). This has been used as an argument against the use of the axiom of choice.
Another argument against the axiom of choice is that it implies the existence of objects that may seem counterintuitive.[10] One example is the Banach–Tarski paradox which says that it is possible to decompose the 3-dimensional solid unit ball into finitely many pieces and, using only rotations and translations, reassemble the pieces into two solid balls each with the same volume as the original. The pieces in this decomposition, constructed using the axiom of choice, are non-measurable sets.
Moreover, paradoxical consequences of the axiom of choice for the no-signaling principle in physics have recently been pointed out.[11]
Despite these seemingly paradoxical results, most mathematicians accept the axiom of choice as a valid principle for proving new results in mathematics. The debate is interesting enough, however, that it is considered of note when a theorem in ZFC (ZF plus AC) is logically equivalent (with just the ZF axioms) to the axiom of choice, and mathematicians look for results that require the axiom of choice to be false, though this type of deduction is less common than the type which requires the axiom of choice to be true.
Theorems of ZF hold true in any model of that theory, regardless of the truth or falsity of the axiom of choice in that particular model. The implications of choice below, including weaker version of the axiom itself, are listed because they are not theorems of ZF. The Banach–Tarski paradox, for example, is neither provable nor disprovable from ZF alone: it is impossible to construct the required decomposition of the unit ball in ZF, but also impossible to prove there is no such decomposition. Such statements can be rephrased as conditional statements, for example, "If AC holds, then the decomposition in the Banach–Tarski paradox exists." Such conditional statements are provable in ZF when the original statements are provable from ZF and the axiom of choice.
In constructive mathematics
As discussed above, in the classical theory of ZFC, the axiom of choice enables nonconstructive proofs in which the existence of a type of object is proved without an explicit instance being constructed. In fact, in set theory and topos theory, Diaconescu's theorem shows that the axiom of choice implies the law of excluded middle. The principle is thus not available in constructive set theory, where non-classical logic is employed.
The situation is different when the principle is formulated in Martin-Löf type theory. There and higher-order Heyting arithmetic, the appropriate statement of the axiom of choice is (depending on approach) included as an axiom or provable as a theorem.[12] A cause for this difference is that the axiom of choice in type theory does not have the extensionality properties that the axiom of choice in constructive set theory does.[13] The type theoretical context is discussed further below.
Different choice principles have been thoroughly studied in the constructive contexts and the principles' status varies between different school and varieties of the constructive mathematics. Some results in constructive set theory use the axiom of countable choice or the axiom of dependent choice, which do not imply the law of the excluded middle. Errett Bishop, who is notable for developing a framework for constructive analysis, argued that an axiom of choice was constructively acceptable, saying
A choice function exists in constructive mathematics, because a choice is implied by the very meaning of existence.[14]
Although the axiom of countable choice in particular is commonly used in constructive mathematics, its use has also been questioned.[15]
Independence
In 1938,[16] Kurt Gödel showed that the negation of the axiom of choice is not a theorem of ZF by constructing an inner model (the constructible universe) which satisfies ZFC and thus showing that ZFC is consistent if ZF itself is consistent. In 1963, Paul Cohen employed the technique of forcing, developed for this purpose, to show that, assuming ZF is consistent, the axiom of choice itself is not a theorem of ZF. He did this by constructing a much more complex model which satisfies ZF¬C (ZF with the negation of AC added as axiom) and thus showing that ZF¬C is consistent.[17]
Together these results establish that the axiom of choice is logically independent of ZF. The assumption that ZF is consistent is harmless because adding another axiom to an already inconsistent system cannot make the situation worse. Because of independence, the decision whether to use the axiom of choice (or its negation) in a proof cannot be made by appeal to other axioms of set theory. The decision must be made on other grounds.
One argument given in favor of using the axiom of choice is that it is convenient to use it because it allows one to prove some simplifying propositions that otherwise could not be proved. Many theorems which are provable using choice are of an elegant general character: the cardinalities of any two sets are comparable, every nontrivial ring with unity has a maximal ideal, every vector space has a basis, every connected graph has a spanning tree, and every product of compact spaces is compact, among many others. Without the axiom of choice, these theorems may not hold for mathematical objects of large cardinality.[clarification needed]
The proof of the independence result also shows that a wide class of mathematical statements, including all statements that can be phrased in the language of Peano arithmetic, are provable in ZF if and only if they are provable in ZFC.[18] Statements in this class include the statement that P = NP, the Riemann hypothesis, and many other unsolved mathematical problems. When one attempts to solve problems in this class, it makes no difference whether ZF or ZFC is employed if the only question is the existence of a proof. It is possible, however, that there is a shorter proof of a theorem from ZFC than from ZF.
The axiom of choice is not the only significant statement which is independent of ZF. For example, the generalized continuum hypothesis (GCH) is not only independent of ZF, but also independent of ZFC. However, ZF plus GCH implies AC, making GCH a strictly stronger claim than AC, even though they are both independent of ZF.
Stronger axioms
The axiom of constructibility and the generalized continuum hypothesis each imply the axiom of choice and so are strictly stronger than it. In class theories such as Von Neumann–Bernays–Gödel set theory and Morse–Kelley set theory, there is an axiom called the axiom of global choice that is stronger than the axiom of choice for sets because it also applies to proper classes. The axiom of global choice follows from the axiom of limitation of size. Tarski's axiom, which is used in Tarski–Grothendieck set theory and states (in the vernacular) that every set belongs to some Grothendieck universe, is stronger than the axiom of choice.
Equivalents
There are important statements that, assuming the axioms of ZF but neither AC nor ¬AC, are equivalent to the axiom of choice.[19] The most important among them are Zorn's lemma and the well-ordering theorem. In fact, Zermelo initially introduced the axiom of choice in order to formalize his proof of the well-ordering theorem.
- Set theory
- Tarski's theorem about choice: For every infinite set A, there is a bijective map between the sets A and A×A.
- Trichotomy: If two sets are given, then either they have the same cardinality, or one has a smaller cardinality than the other.
- Given two non-empty sets, one has a surjection to the other.
- Every surjective function has a right inverse.
- The Cartesian product of any family of nonempty sets is nonempty. In other words, every family of nonempty sets has a choice function (i.e. a function which maps each of the nonempty sets to one of its elements).
- König's theorem: Colloquially, the sum of a sequence of cardinals is strictly less than the product of a sequence of larger cardinals. (The reason for the term "colloquially" is that the sum or product of a "sequence" of cardinals cannot itself be defined without some aspect of the axiom of choice.)
- Well-ordering theorem: Every set can be well-ordered. Consequently, every cardinal has an initial ordinal.
- Every element of a partially ordered set S is the minimal element of a well-ordered subset having no strict upper bound in S.
- Zorn's lemma: Every non-empty partially ordered set in which every chain (i.e., totally ordered subset) has an upper bound contains at least one maximal element.
- Hausdorff maximal principle: Every partially ordered set has a maximal chain. Equivalently, in any partially ordered set, every chain can be extended to a maximal chain.
- Tukey's lemma: Every non-empty collection of finite character has a maximal element with respect to inclusion.
- Antichain principle: Every partially ordered set has a maximal antichain. Equivalently, in any partially ordered set, every antichain can be extended to a maximal antichain.
- Abstract algebra
- Every vector space has a basis (i.e., a linearly independent spanning subset). In other words, vector spaces are equivalent to free modules.[20]
- Krull's theorem: Every unital ring (other than the trivial ring) contains a maximal ideal. Equivalently, in any nontrivial unital ring, every ideal can be extended to a maximal ideal.
- For every non-empty set S there is a binary operation defined on S that gives it a group structure.[21] (A cancellative binary operation is enough, see group structure and the axiom of choice.)
- Every free abelian group is projective.[22]
- Baer's criterion: Every divisible abelian group is injective.[22]
- Every set is a projective object in the category Set of sets.[23][24]
- Functional analysis
- The closed unit ball of the dual of a normed vector space over the reals has an extreme point.
- Point-set topology
- The Cartesian product of any family of connected topological spaces is connected.
- Tychonoff's theorem: The Cartesian product of any family of compact topological spaces is compact.
- In the product topology, the closure of a product of subsets is equal to the product of the closures.
- Mathematical logic
- If S is a set of sentences of first-order logic and B is a consistent subset of S, then B is included in a set that is maximal among consistent subsets of S. The special case where S is the set of all first-order sentences in a given signature is weaker, equivalent to the Boolean prime ideal theorem; see the section "Weaker forms" below.
- Algebraic topology
- Every connected graph has a spanning tree. Equivalently, every nonempty graph has a spanning forest.[25]
Category theory
There are several results in category theory which invoke the axiom of choice for their proof. These results might be weaker than, equivalent to, or stronger than the axiom of choice, depending on the strength of the technical foundations. For example, if one defines categories in terms of sets, that is, as sets of objects and morphisms (usually called a small category), or even locally small categories, whose hom-objects are sets, then there is no category of all sets, and so it is difficult for a category-theoretic formulation to apply to all sets. On the other hand, other foundational descriptions of category theory are considerably stronger, and an identical category-theoretic statement of choice may be stronger than the standard formulation, à la class theory, mentioned above.
Examples of category-theoretic statements which require choice include:
- Every small category has a skeleton.
- If two small categories are weakly equivalent, then they are equivalent.
- Every continuous functor on a small-complete category which satisfies the appropriate solution set condition has a left-adjoint (the Freyd adjoint functor theorem).
Weaker forms
There are several weaker statements that are not equivalent to the axiom of choice, but are closely related. One example is the axiom of dependent choice (DC). A still weaker example is the axiom of countable choice (ACω or CC), which states that a choice function exists for any countable set of nonempty sets. These axioms are sufficient for many proofs in elementary mathematical analysis, and are consistent with some principles, such as the Lebesgue measurability of all sets of reals, that are disprovable from the full axiom of choice.
Given an ordinal parameter α ≥ ω+2 — for every set S with rank less than α, S is well-orderable. Given an ordinal parameter α ≥ 1 — for every set S with Hartogs number less than ωα, S is well-orderable. As the ordinal parameter is increased, these approximate the full axiom of choice more and more closely.
Other choice axioms weaker than axiom of choice include the Boolean prime ideal theorem and the axiom of uniformization. The former is equivalent in ZF to Tarski's 1930 ultrafilter lemma: every filter is a subset of some ultrafilter.
Results requiring AC (or weaker forms) but weaker than it
One of the most interesting aspects of the axiom of choice is the large number of places in mathematics that it shows up. Here are some statements that require the axiom of choice in the sense that they are not provable from ZF but are provable from ZFC (ZF plus AC). Equivalently, these statements are true in all models of ZFC but false in some models of ZF.
- Set theory
- The ultrafilter lemma (with ZF) can be used to prove the Axiom of choice for finite sets: Given and a collection of non-empty finite sets, their product is not empty.[26]
- The union of any countable family of countable sets is countable (this requires countable choice but not the full axiom of choice).
- If the set A is infinite, then there exists an injection from the natural numbers N to A (see Dedekind infinite).[27]
- Eight definitions of a finite set are equivalent.[28]
- Every infinite game in which is a Borel subset of Baire space is determined.
- Measure theory
- The Vitali theorem on the existence of non-measurable sets, which states that there exists a subset of the real numbers that is not Lebesgue measurable.
- There exist Lebesgue-measurable subsets of the real numbers that are not Borel sets. That is, the Borel σ-algebra on the real numbers (which is generated by all real intervals) is distinct from the Lebesgue-measure σ-algebra on the real numbers.
- The Hausdorff paradox.
- The Banach–Tarski paradox.
- Algebra
- Every field has an algebraic closure.
- Every field extension has a transcendence basis.
- Every infinite-dimensional vector space contains an infinite linearly independent subset (this requires dependent choice, but not the full axiom of choice).
- Stone's representation theorem for Boolean algebras needs the Boolean prime ideal theorem.
- The Nielsen–Schreier theorem, that every subgroup of a free group is free.
- The additive groups of R and C are isomorphic.[29][30]
- Functional analysis
- The Hahn–Banach theorem in functional analysis, allowing the extension of linear functionals.
- The theorem that every Hilbert space has an orthonormal basis.
- The Banach–Alaoglu theorem about compactness of sets of functionals.
- The Baire category theorem about complete metric spaces, and its consequences, such as the open mapping theorem and the closed graph theorem.
- On every infinite-dimensional topological vector space there is a discontinuous linear map.
- General topology
- A uniform space is compact if and only if it is complete and totally bounded.
- Every Tychonoff space has a Stone–Čech compactification.
- Mathematical logic
- Gödel's completeness theorem for first-order logic: every consistent set of first-order sentences has a completion. That is, every consistent set of first-order sentences can be extended to a maximal consistent set.
- The compactness theorem: If is a set of first-order (or alternatively, zero-order) sentences such that every finite subset of has a model, then has a model.[31]
Possibly equivalent implications of AC
There are several historically important set-theoretic statements implied by AC whose equivalence to AC is open. The partition principle, which was formulated before AC itself, was cited by Zermelo as a justification for believing AC. In 1906, Russell declared PP to be equivalent, but whether the partition principle implies AC is still the oldest open problem in set theory,[32] and the equivalences of the other statements are similarly hard old open problems. In every known model of ZF where choice fails, these statements fail too, but it is unknown if they can hold without choice.
- Set theory
- Partition principle: if there is a surjection from A to B, there is an injection from B to A. Equivalently, every partition P of a set S is less than or equal to S in size.
- Converse Schröder–Bernstein theorem: if two sets have surjections to each other, they are equinumerous.
- Weak partition principle: if there is a injection and a surjection from A to B, then A and B are equinumerous. Equivalently, a partition of a set S cannot be strictly larger than S. If WPP holds, this already implies the existence of a non-measurable set. Each of the previous three statements is implied by the preceding one, but it is unknown if any of these implications can be reversed.
- There is no infinite decreasing sequence of cardinals. The equivalence was conjectured by Schoenflies in 1905.
- Abstract algebra
- Hahn embedding theorem: Every ordered abelian group G order-embeds as a subgroup of the additive group endowed with a lexicographical order, where Ω is the set of Archimedean equivalence classes of G. This equivalence was conjectured by Hahn in 1907.
Stronger forms of the negation of AC
If we abbreviate by BP the claim that every set of real numbers has the property of Baire, then BP is stronger than ¬AC, which asserts the nonexistence of any choice function on perhaps only a single set of nonempty sets. Strengthened negations may be compatible with weakened forms of AC. For example, ZF + DC[33] + BP is consistent, if ZF is.
It is also consistent with ZF + DC that every set of reals is Lebesgue measurable; however, this consistency result, due to Robert M. Solovay, cannot be proved in ZFC itself, but requires a mild large cardinal assumption (the existence of an inaccessible cardinal). The much stronger axiom of determinacy, or AD, implies that every set of reals is Lebesgue measurable, has the property of Baire, and has the perfect set property (all three of these results are refuted by AC itself). ZF + DC + AD is consistent provided that a sufficiently strong large cardinal axiom is consistent (the existence of infinitely many Woodin cardinals).
Quine's system of axiomatic set theory, New Foundations (NF), takes its name from the title ("New Foundations for Mathematical Logic") of the 1937 article which introduced it. In the NF axiomatic system, the axiom of choice can be disproved.[34]
Statements consistent with the negation of AC
There are models of Zermelo-Fraenkel set theory in which the axiom of choice is false. We shall abbreviate "Zermelo-Fraenkel set theory plus the negation of the axiom of choice" by ZF¬C. For certain models of ZF¬C, it is possible to validate the negation of some standard ZFC theorems. As any model of ZF¬C is also a model of ZF, it is the case that for each of the following statements, there exists a model of ZF in which that statement is true
- There is a set that can be partitioned into strictly more equivalence classes than the original set has elements, and a function whose domain is strictly smaller than its range. In fact, this is the case in all known models.
- There is a function f from the real numbers to the real numbers such that f is not continuous at a, but f is sequentially continuous at a, i.e., for any sequence {xn} converging to a, limn f(xn)=f(a).
- There is an infinite set of real numbers without a countably infinite subset.
- The real numbers are a countable union of countable sets.[35] This does not imply that the real numbers are countable: As pointed out above, to show that a countable union of countable sets is itself countable requires the Axiom of countable choice.
- There is a field with no algebraic closure.
- In all models of ZF¬C there is a vector space with no basis.
- There is a vector space with two bases of different cardinalities.
- There is a free complete boolean algebra on countably many generators.[36]
- There is a set that cannot be linearly ordered.
- There exists a model of ZF¬C in which every set in Rn is measurable. Thus it is possible to exclude counterintuitive results like the Banach–Tarski paradox which are provable in ZFC. Furthermore, this is possible whilst assuming the Axiom of dependent choice, which is weaker than AC but sufficient to develop most of real analysis.
- In all models of ZF¬C, the generalized continuum hypothesis does not hold.
For proofs, see (Jech 2008).
Additionally, by imposing definability conditions on sets (in the sense of descriptive set theory) one can often prove restricted versions of the axiom of choice from axioms incompatible with general choice. This appears, for example, in the Moschovakis coding lemma.
Axiom of choice in type theory
In type theory, a different kind of statement is known as the axiom of choice. This form begins with two types, σ and τ, and a relation R between objects of type σ and objects of type τ. The axiom of choice states that if for each x of type σ there exists a y of type τ such that R(x,y), then there is a function f from objects of type σ to objects of type τ such that R(x,f(x)) holds for all x of type σ:
Unlike in set theory, the axiom of choice in type theory is typically stated as an axiom scheme, in which R varies over all formulas or over all formulas of a particular logical form.
Quotations
The axiom of choice is obviously true, the well-ordering principle obviously false, and who can tell about Zorn's lemma?—Jerry Bona[37]
This is a joke: although the three are all mathematically equivalent, many mathematicians find the axiom of choice to be intuitive, the well-ordering principle to be counterintuitive, and Zorn's lemma to be too complex for any intuition.
The Axiom of Choice is necessary to select a set from an infinite number of pairs of socks, but not an infinite number of pairs of shoes.
The observation here is that one can define a function to select from an infinite number of pairs of shoes, for example by choosing the left shoe from each pair. Without the axiom of choice, one cannot assert that such a function exists for pairs of socks, because left and right socks are (presumably) indistinguishable.
Tarski tried to publish his theorem [the equivalence between AC and "every infinite set A has the same cardinality as A × A", see above] in Comptes Rendus, but Fréchet and Lebesgue refused to present it. Fréchet wrote that an implication between two well known [true] propositions is not a new result, and Lebesgue wrote that an implication between two false propositions is of no interest.
Polish-American mathematician Jan Mycielski relates this anecdote in a 2006 article in the Notices of the AMS.[39]
The axiom gets its name not because mathematicians prefer it to other axioms.
This quote comes from the famous April Fools' Day article in the computer recreations column of the Scientific American, April 1989.
Notes
- ↑ Zermelo 1904.
- ↑ Jech 1977, p. 351
- ↑ Jech, 1977, p. 348ff; Martin-Löf 2008, p. 210. According to Mendelson 1964, p. 201:
- The status of the Axiom of Choice has become less controversial in recent years. To most mathematicians it seems quite plausible and it has so many important applications in practically all branches of mathematics that not to accept it would seem to be a wilful hobbling of the practicing mathematician.
- ↑ Rosenberg, Steven (21 December 2021). An Invitation to Abstract Algebra. CRC Press. ISBN 9781000516333. https://books.google.com/books?id=KWlPEAAAQBAJ&pg=PA316.
- ↑ Herrlich 2006, p. 9. According to Suppes 1972, p. 243, this was the formulation of the axiom of choice which was originally given by Zermelo 1904. See also Halmos 1960, p. 60 for this formulation.
- ↑ Suppes 1972, p. 240.
- ↑ Tourlakis (2003), pp. 209–210, 215–216.
- ↑ Foundations of set theory (2nd ed.), Amsterdam-London: North-Holland Publishing Co., 1973, pp. 69–70, ISBN 9780080887050, https://books.google.com/books?id=ah2bwOwc06MC&pg=PA69.
- ↑ Rosenbloom, Paul C. (2005), The Elements of Mathematical Logic, Courier Dover Publications, p. 147, ISBN 9780486446172, https://books.google.com/books?id=089eY-s33EsC&pg=PA147.
- ↑ Dawson, J. W. (August 2006), "Shaken Foundations or Groundbreaking Realignment? A Centennial Assessment of Kurt Gödel's Impact on Logic, Mathematics, and Computer Science", Proc. 21st Annual IEEE Symposium on Logic in Computer Science (LICS 2006), pp. 339–341, doi:10.1109/LICS.2006.47, ISBN 978-0-7695-2631-7, "The axiom of choice, though it had been employed unconsciously in many arguments in analysis, became controversial once made explicit, not only because of its non-constructive character, but because it implied such extremely unintuitive consequences as the Banach–Tarski paradox.".
- ↑ Baumeler, Ä., Dakić, B. and Del Santo, F., 2022. The Axiom of Choice and the No-Signaling Principle, arXiv preprint — arXiv:2206.08467.
- ↑ Per Martin-Löf, Intuitionistic type theory, 1980. Anne Sjerp Troelstra, Metamathematical investigation of intuitionistic arithmetic and analysis, Springer, 1973.
- ↑ Martin-Löf, Per (2006). "100 Years of Zermelo's Axiom of Choice: What was the Problem with It?". The Computer Journal 49 (3): 345–350. doi:10.1093/comjnl/bxh162. Bibcode: 1980CompJ..23..262L.
- ↑ Errett Bishop and Douglas S. Bridges, Constructive analysis, Springer-Verlag, 1985.
- ↑ Fred Richman, "Constructive mathematics without choice", in: Reuniting the Antipodes—Constructive and Nonstandard Views of the Continuum (P. Schuster et al., eds), Synthèse Library 306, 199–205, Kluwer Academic Publishers, Amsterdam, 2001.
- ↑ Gödel, Kurt (9 November 1938). "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis". Proceedings of the National Academy of Sciences of the United States of America 24 (12): 556–557. doi:10.1073/pnas.24.12.556. PMID 16577857. Bibcode: 1938PNAS...24..556G.
- ↑ Cohen, Paul (2019). "The Independence of the Axiom of Choice". https://stacks.stanford.edu/file/druid:pd104gy5838/SCM0405.pdf.
- ↑ This is because arithmetical statements are absolute to the constructible universe L. Shoenfield's absoluteness theorem gives a more general result.
- ↑ See Moore 2013, pp. 330–334, for a structured list of 74 equivalents. See Howard & Rubin 1998, pp. 11–16, for 86 equivalents with source references.
- ↑ Blass, Andreas (1984). "Axiomatic set theory (Boulder, Colo., 1983)". 31. Providence, RI: American Mathematical Society. pp. 31–33. doi:10.1090/conm/031/763890.
- ↑ A. Hajnal, A. Kertész: Some new algebraic equivalents of the axiom of choice, Publ. Math. Debrecen, 19(1972), 339–340, see also H. Rubin, J. Rubin, Equivalents of the axiom of choice, II, North-Holland, 1985, p. 111.
- ↑ 22.0 22.1 Blass, Andreas (1979). "Injectivity, Projectivity and the Axiom of Choice". Transactions of the American Mathematical Society 255: 31–59. doi:10.2307/1998165.
- ↑ Awodey, Steve (2010). Category theory (2nd ed.). Oxford: Oxford University Press. pp. 20–24. ISBN 978-0199237180. OCLC 740446073. https://archive.org/details/categorytheoryse00awod.
- ↑ projective object in nLab
- ↑ Serre, Jean-Pierre (2003), Trees, Springer Monographs in Mathematics, Springer, p. 23; Soukup, Lajos (2008), "Infinite combinatorics: from finite to infinite", Horizons of combinatorics, Bolyai Society Mathematical Studies, 17, Berlin: Springer, pp. 189–213, doi:10.1007/978-3-540-77200-2_10, ISBN 978-3-540-77199-9. See in particular Theorem 2.1, pp. 192–193.
- ↑ Muger, Michael (2020). Topology for the Working Mathematician.
- ↑ It is shown by Jech 2008, pp. 119–131, that the axiom of countable choice implies the equivalence of infinite and Dedekind-infinite sets, but that the equivalence of infinite and Dedekind-infinite sets does not imply the axiom of countable choice in ZF.
- ↑ It was shown by Lévy 1958 and others using Mostowski models that eight definitions of a finite set are independent in ZF without AC, although they are equivalent when AC is assumed. The definitions are I-finite, Ia-finite, II-finite, III-finite, IV-finite, V-finite, VI-finite and VII-finite. I-finiteness is the same as normal finiteness. IV-finiteness is the same as Dedekind-finiteness.
- ↑ "[FOM Are (C,+) and (R,+) isomorphic"]. 21 February 2006. http://www.cs.nyu.edu/pipermail/fom/2006-February/009959.html.
- ↑ Ash, C. J. (1975). "A consequence of the axiom of choice". Journal of the Australian Mathematical Society 19 (3): 306–308. doi:10.1017/S1446788700031505.
- ↑ Schechter 1996, pp. 391–392.
- ↑ "On the Partition Principle". https://karagila.org/2014/on-the-partition-principle/.
- ↑ Axiom of dependent choice
- ↑ "Quine's New Foundations". Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/quine-nf/. Retrieved 2017-11-10.
- ↑ Jech 2008, pp. 142–144, Theorem 10.6 with proof.
- ↑ Stavi, Jonathan (1974). "A model of ZF with an infinite free complete Boolean algebra". Israel Journal of Mathematics 20 (2): 149–163. doi:10.1007/BF02757883.
- ↑ "The axiom of choice", Handbook of Logic and Proof Techniques for Computer Science, Springer, 2002, pp. 121–126, doi:10.1007/978-1-4612-0115-1_9, ISBN 978-1-4612-6619-8.
- ↑ The boots-and-socks metaphor was given in 1919 by Russell 1993, pp. 125–127. He suggested that a millionaire might have ℵ0 pairs of boots and ℵ0 pairs of socks.
Among boots we can distinguish right and left, and therefore we can make a selection of one out of each pair, namely, we can choose all the right boots or all the left boots; but with socks no such principle of selection suggests itself, and we cannot be sure, unless we assume the multiplicative axiom, that there is any class consisting of one sock out of each pair.
Russell generally used the term "multiplicative axiom" for the axiom of choice. Referring to the ordering of a countably infinite set of pairs of objects, he wrote:
There is no difficulty in doing this with the boots. The pairs are given as forming an ℵ0, and therefore as the field of a progression. Within each pair, take the left boot first and the right second, keeping the order of the pair unchanged; in this way we obtain a progression of all the boots. But with the socks we shall have to choose arbitrarily, with each pair, which to put first; and an infinite number of arbitrary choices is an impossibility. Unless we can find a rule for selecting, i.e. a relation which is a selector, we do not know that a selection is even theoretically possible.Russell then suggests using the location of the centre of mass of each sock as a selector.
- ↑ "A system of axioms of set theory for the rationalists", Notices of the American Mathematical Society 53 (2): 206–213, 2006, https://www.ams.org/journals/notices/200602/fea-mycielski.pdf.
References
- Halmos, Paul R. (1960). Naive Set Theory. The University Series in Undergraduate Mathematics. Princeton, NJ: van Nostrand Company.
- Herrlich, Horst (2006). Axiom of Choice. Lecture Notes in Math. 1876. Berlin: Springer-Verlag. ISBN 978-3-540-30989-5.
- Howard, Paul; Rubin, Jean E. (1998). Consequences of the axiom of choice. Mathematical Surveys and Monographs. 59. Providence, Rhode Island: American Mathematical Society. ISBN 9780821809778. https://archive.org/details/consequencesofax0000howa.
- The axiom of choice. Mineola, New York: Dover Publications. 2008. ISBN 978-0-486-46624-8.
- Jech, Thomas (1977). "About the Axiom of Choice". in John Barwise. Handbook of Mathematical Logic.
- Lévy, Azriel (1958). "The independence of various definitions of finiteness". Fundamenta Mathematicae 46: 1–13. doi:10.4064/fm-46-1-1-13. http://matwbn.icm.edu.pl/ksiazki/fm/fm46/fm4611.pdf.
- Per Martin-Löf, "100 years of Zermelo's axiom of choice: What was the problem with it?", in Logicism, Intuitionism, and Formalism: What Has Become of Them?, Sten Lindström, Erik Palmgren, Krister Segerberg, and Viggo Stoltenberg-Hansen, editors (2008). ISBN 1-4020-8925-2
- Mendelson, Elliott (1964). Introduction to Mathematical Logic. New York: Van Nostrand Reinhold.
- Moore, Gregory H. (1982). Zermelo's axiom of choice, Its origins, development and influence. Springer. ISBN 978-0-387-90670-6., available as a Dover Publications reprint, 2013, ISBN 0-486-48841-1.
- Moore, Gregory H (2013). Zermelo's axiom of choice: Its origins, development & influence. Mineola, New York: Dover Publications. ISBN 978-0-486-48841-7.
- Herman Rubin, Jean E. Rubin: Equivalents of the axiom of choice. North Holland, 1963. Reissued by Elsevier, April 1970. ISBN 0-7204-2225-6.
- Herman Rubin, Jean E. Rubin: Equivalents of the Axiom of Choice II. North Holland/Elsevier, July 1985, ISBN 0-444-87708-8.
- Russell, Bertrand (1993). Introduction to mathematical philosophy. New York: Dover Publications. ISBN 978-0-486-27724-0.
- Schechter, Eric (1996). Handbook of Analysis and Its Foundations. San Diego, CA: Academic Press. ISBN 978-0-12-622760-4. OCLC 175294365.
- Suppes, Patrick (1972). Axiomatic set theory. Mineola, New York: Dover. ISBN 978-0-486-61630-8. https://archive.org/details/axiomaticsettheo00supp_0.
- George Tourlakis, Lectures in Logic and Set Theory. Vol. II: Set Theory, Cambridge University Press , 2003. ISBN 0-511-06659-7
- Zermelo, Ernst (1904). "Beweis, dass jede Menge wohlgeordnet werden kann" (reprint). Mathematische Annalen 59 (4): 514–16. doi:10.1007/BF01445300. http://gdz.sub.uni-goettingen.de/no_cache/en/dms/load/img/?IDDOC=28526.
- Ernst Zermelo, "Untersuchungen über die Grundlagen der Mengenlehre I," Mathematische Annalen 65: (1908) pp. 261–81. PDF download via digizeitschriften.de
- Translated in: Jean van Heijenoort, 2002. From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931. New edition. Harvard University Press. ISBN 0-674-32449-8
- 1904. "Proof that every set can be well-ordered," 139-41.
- 1908. "Investigations in the foundations of set theory I," 199–215.
- Translated in: Jean van Heijenoort, 2002. From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931. New edition. Harvard University Press. ISBN 0-674-32449-8
External links
- Axiom of Choice entry in the Springer Encyclopedia of Mathematics.
- Axiom of Choice and Its Equivalents entry at ProvenMath. Includes formal statement of the Axiom of Choice, Hausdorff's Maximal Principle, Zorn's Lemma and formal proofs of their equivalence down to the finest detail.
- Consequences of the Axiom of Choice , based on the book by Paul Howard and Jean Rubin.
- The Axiom of Choice entry by John Lane Bell in the Stanford Encyclopedia of Philosophy.
 |
