Finance:History of microeconomics

Short description: History of the development of microeconomics as a study

Top row: Jevons, Walras, Marshall
Middle row: Paul Douglas, Edward Chamberlin, Paul Samuelson
Bottom row: Michael Spence, George Akerlof, Joseph Stiglitz

Microeconomics is the study of the behaviour of individuals and small impacting organisations in making decisions on the allocation of limited resources. The modern field of microeconomics arose as an effort of neoclassical economics school of thought to put economic ideas into mathematical mode.

Origins

Microeconomics descends philosophically from Utilitarianism and mathematically from the work of Daniel Bernoulli.

Utilitarianism

Utilitarianism as a distinct ethical position only emerged in the 18th century, usually credited to Jeremy Bentham, but there were earlier writers, such as Epicurus who presented similar theories. Bentham's An Introduction to the Principles of Morals and Legislation (1780) begins by defining the principle of utility:

"II. The principle of utility is the foundation of the present work: it will be proper therefore at the outset to give an explicit and determinate account of what is meant by it. By the principle of utility is meant that principle which approves or disapproves of every action whatsoever. according to the tendency it appears to have to augment or diminish the happiness of the party whose interest is in question: or, what is the same thing in other words to promote or to oppose that happiness. I say of every action whatsoever, and therefore not only of every action of a private individual, but of every measure of government.

III. By utility is meant that property in any object, whereby it tends to produce benefit, advantage, pleasure, good, or happiness, (all this in the present case comes to the same thing) or (what comes again to the same thing) to prevent the happening of mischief, pain, evil, or unhappiness to the party whose interest is considered: if that party be the community in general, then the happiness of the community: if a particular individual, then the happiness of that individual.

IV. The interest of the community is one of the most general expressions that can occur in the phraseology of morals: no wonder that the meaning of it is often lost. When it has a meaning, it is this. The community is a fictitious body, composed of the individual persons who are considered as constituting as it were its members. The interest of the community then is, what is it?— the sum of the interests of the several members who compose it."

He also defined how pleasure can be measured:

"I.Pleasures then, and the avoidance of pains, are the ends which the legislator has in view: it behoves him therefore to understand their value. Pleasures and pains are the instruments he has to work with: it behoves him therefore to understand their force, which is again, in other words, their value.

II. To a person considered by himself, the value of a pleasure or pain considered by itself, will be greater or less, according to the four following circumstances:

Its intensity. Its duration. Its certainty or uncertainty. Its propinquity or remoteness.

III. These are the circumstances which are to be considered in estimating a pleasure or a pain considered each of them by itself. But when the value of any pleasure or pain is considered for the purpose of estimating the tendency of any act by which it is produced, there are two other circumstances to be taken into the account; these are,

Its fecundity, or the chance it has of being followed by sensations of the same kind: that is, pleasures, if it be a pleasure: pains, if it be a pain. Its purity, or the chance it has of not being followed by sensations of the opposite kind: that is, pains, if it be a pleasure: pleasures, if it be a pain.

These two last, however, are in strictness scarcely to be deemed properties of the pleasure or the pain itself; they are not, therefore, in strictness to be taken into the account of the value of that pleasure or that pain. They are in strictness to be deemed properties only of the act, or other event, by which such pleasure or pain has been produced; and accordingly are only to be taken into the account of the tendency of such act or such event."

A list of utilitarians also includes James Mill, Stuart Mill and William Paley.

Expected utility

Daniel Bernoulli wrote in 1738 this about risk:

"EVER SINCE mathematicians first began to study the measurement of risk there has been general agreement on the following proposition: Expected values are computed by multiplying each possible gain by the number of ways in which it can occur, and then dividing the sum of these products by the total number of possible cases where, in this theory, the consideration of cases which are all of the same probability is insisted upon. If this rule be accepted, what remains to be done within the framework of this theory amounts to the enumeration of all alternatives, their breakdown into equi-probable cases and, finally, their insertion into corresponding classifications."

Utility as function of wealth as described by Bernoulli.

He states that as an individual wealth increases so will his utility increase in inverse proportion to quantity of goods already possessed. This is called diminishing marginal utility in microeconomics textbooks. He also describes the following problem.

"My most honorable cousin the celebrated Nicolas Bernoulli, Professor utriusque iuris at the University of Basle, once submitted five problems to the highly distinguished mathematician Montmort. These problems are reproduced in the work L'analyse sur les jeux de hazard de M. de Montmort, p. 402. The last of these problems runs as follows: Peter tosses a coin and continues to do so until it should land "heads" when it comes to the ground. He agrees to give Paul one ducat if he gets "heads" on the very first throw, two ducats if he gets it on the second, four if on the third, eight if on the fourth, and so on, so that with each additional throw the number of ducats he must pay is doubled. Suppose we seek to determine the value of Paul's expectation."

This is referred to in the literature as the St. Petersburg paradox.

Traditional marginalism

Classic duopoly model of Cournot: reaction functions of both firms (R1 and R2) are derived by imposing profit maximisation, the Nash equilibrium is given by intersection of R1 and R2. At equilibrium no firm has a rational self-interest in changing quantities produced.

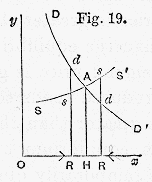
An early attempt of mathematizing economics was made by Antoine Augustine Cournot in Researches on the Mathematical Principles of the Theory of Wealth (1838): he described mathematically the law of demand, monopoly, and the spring water duopoly that now bears his name. Later, William Stanley Jevons's Theory of Political Economy (1871), Carl Menger's Principles of Economics (1871), and Léon Walras's Elements of Pure Economics: Or the theory of social wealth (1874–77) gave way to what was called the Marginal Revolution. Some common ideas behind those works were models or arguments characterized by rational economic agents maximising utility under a budget constraint. This arose as a necessity of arguing against the labour theory of value associated with classical economists such as Adam Smith, David Ricardo and Karl Marx, although the theory itself can traced back to earlier writers. Walras also went as far as developing the concept of general equilibrium of an economy.

Smith published The Wealth of Nations in 1776, his emphasis is on the labour saving function of money:

"The real price of every thing, what every thing really costs to the man who wants to acquire it, is the toil and trouble of acquiring it. What every thing is really worth to the man who has acquired it, and who wants to dispose of it or exchange it for something else, is the toil and trouble which it can save to himself, and which it can impose upon other people. What is bought with money or with goods is purchased by labour, as much as what we acquire by the toil of our own body. That money or those goods indeed save us this toil. They contain the value of a certain quantity of labour which we exchange for what is supposed at the time to contain the value of an equal quantity. Labour was the first price, the original purchase-money that was paid for all things. It was not by gold or by silver, but by labour, that all the wealth of the world was originally purchased; and its value, to those who possess it, and who want to exchange it for some new productions, is precisely equal to the quantity of labour which it can enable them to purchase or command."

Regarding value, Smith wrote:

"The word VALUE, it is to be observed, has two different meanings, and sometimes expresses the utility of some particular object, and sometimes the power of purchasing other goods which the possession of that object conveys. The one may be called ‘value in use;’ the other, ‘value in exchange.’ The things which have the greatest value in use have frequently little or no value in exchange; and on the contrary, those which have the greatest value in exchange have frequently little or no value in use. Nothing is more useful than water: but it will purchase scarce any thing; scarce any thing can be had in exchange for it. A diamond, on the contrary, has scarce any value in use; but a very great quantity of other goods may frequently be had in exchange for it."

A labour theory of value can be understood as a theory that argues that economic value is determined by the amount of socially necessary labour time: this can be found in the theorization of Ricardo who said "If the quantity of labour realized in commodities, regulate their exchangeable value, every increase of the quantity of labour must augment the value of that commodity on which it is exercised, as every diminution must lower it." and Marx who said "A use-value, or useful article, therefore, has value only because human labour in the abstract has been embodied or materialised in it. How, then, is the magnitude of this value to be measured? Plainly, by the quantity of the value-creating substance, the labour, contained in the article. The quantity of labour, however, is measured by its duration, and labour-time in its turn finds its standard in weeks, days, and hours.". A subjective theory of value on the other hand derives value from subjective preferences.

Carl Menger, born in Galicia and considered by Hayek as the founder of the Austrian school of economics, distinguished goods in consumption goods (first order goods) and means of production (higher-order goods). He said:

"While quantities of fresh drinking water in regions abounding in springs, raw timber in virgin forests, and in some countries even land, do not have economic character, these same goods exhibit economic character in other places at the same time. Examples are no less numerous of goods that do not have economic character at a particular time and place but which, at this same place, attain economic character at another time. These differences between goods and their changeability cannot, therefore, be based on the properties of the goods. On the contrary, one can, if in doubt, convince oneself in all cases, by an exact and careful examination of these relationships, that when goods of the same kind have a different character in two different places at the same time, the relationship between requirements and available quantities is different in these two places, and that wherever, in one place, goods that originally had non-economic character become economic goods, or where the opposite takes place, a change has occurred in this quantitative relationship. According to our analysis, there can be only two kinds of reasons why a non-economic good becomes an economic good: an increase in human requirements or a diminution of the available quantity."

The paradox of value: water is cheaper than diamonds, yet it is essential for humans. Why?

• 

  Water

• 

  Diamond

Jevons could be considered a follower of Bentham, as can be read in his commentary upon the paradox of value:

"In the first place, utility, though a quality of things, is no inherent quality. It might be more accurately described, perhaps, as a circumstance of things arising out of their relation to man's requirements. As Mr. Senior most accurately says, "Utility denotes no intrinsic quality in the things which we call useful it merely expresses then relations to the pains and pleasures of mankind". We can never, therefore, say absolutely that some objects have utility and others have not. The ore lying in the mine, the diamond escaping the eye of the searcher, the wheat lying unreaped, the fruit ungathered for want of consumers, have not utility at all. The most wholesome and necessary kinds of food are useless there are hands to collect and mouths to eat them. Nor, when we consider the matter closely, call we say that all portions of the same commodity possess equal utility. Water, for instance, may be roughly described as the most useful of all substances. A quart of water per day has the high utility of saving a person from dying in a most distressing manner. Several gallons a day may possess much utility for such purposes as cooking and washing; but after an adequate supply is secured for these uses, any additional quantity is a matter of indifference. All that we can say, then, is, that water, up to a certain quantity, is indispensable ; that further quantities will have various degrees of utility ; but that beyond a certain point the utility appears to cease. Exactly the same considerations apply more or less clearly to every other article. A pound of bread per day supplied to a person saves him from starvation, and has the highest conceivable utility. A second pound per day has also no slight utility: it keeps him in a state of comparative plenty, though it be not altogether indispensable. A third pound would begin to be superfluous. It is clear, then, that utility is not proportional to commodity: the very same articles vary in utility according as we already possess more or less of the same article. The like may be said of other things. One suit of clothes per annum is necessary, a second convenient, a third desirable, a fourth not unacceptable; but we, sooner or later, reach a point at which further supplies are not desired with any perceptible force, unless it be for subsequent use."

Alfred Marshall's textbook, Principles of Economics was first published in 1890 and became the dominant textbook in England for a generation. His main point was that Jevons went too far in emphasising utility as an attempt to explain prices over costs of production. In the book he writes:

"There are few writers of modern times who have approached as near to the brilliant originality of Ricardo as Jevons has done. But he appears to have judged both Ricardo and Mill harshly, and to have attributed to them doctrines narrower and less scientific than those they really held. Also, his desire to emphasise an aspect of value to which they had given insufficient prominence, was probably in some measure accountable for his saying, "Repeated reflection and inquiry have led me to the somewhat novel opinion that value depends entirely upon utility." (Theory, p. 1) This statement seems to be no less one-sided and fragmentary, and much more misleading, than that into which Ricardo often glided with careless brevity, as to the dependence of value on cost of production; but which he never regarded as more than a part of a larger doctrine, the rest of which he had tried to explain."

In the same appendix he further states:

"Perhaps Jevons' antagonism to Ricardo and Mill would have been less if he had not himself fallen into the habit of speaking of relations which really exist only between demand price and value as though they held between utility and value; and if he had emphasised as Cournot had done, and as the use of mathematical forms might have been expected to lead him to do, that fundamental symmetry of the general relations in which demand and supply stand to value, which coexists with striking differences in the details of those relations. We must not indeed forget that, at the time at which he wrote, the demand side of the theory of value had been much neglected; and that he did excellent service by calling attention to it and developing it. There are few thinkers whose claims on our gratitude are as high and as various as those of Jevons: but that must not lead us to accept hastily his criticisms on his great predecessors."

Marshall's diagram: SS' is the supply curve, DD' is the demand curve and A is the equilibrium

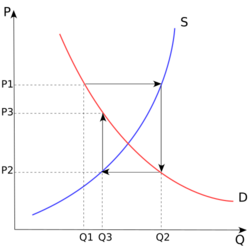
Marshall's idea of solving the controversy was that the demand curve could be derived by aggregating individual consumer demand curves, which were themselves based on the consumer problem of maximising utility. The supply curve could be derived by superimposing a representative firm supply curves for the factors of production and then market equilibrium would be given by the intersection of demand and supply curves. He also introduced the notion of different market periods: mainly short run and long run. This set of ideas gave way to what economists call perfect competition, now found in the standard microeconomics texts, even though Marshall himself had stated:

"The process of substitution, of which we have been discussing the tendencies, is one form of competition; and it may be well to insist again that we do not assume that competition is perfect. Perfect competition requires a perfect knowledge of the state of the market; and though no great departure from the actual facts of life is involved in assuming this knowledge on the part of dealers when we are considering the course of business in Lombard Street, the Stock Exchange, or in a wholesale Produce Market; it would be an altogether unreasonable assumption to make when we are examining the causes that govern the supply of labour in any of the lower grades of industry. For if a man had sufficient ability to know everything about the market for his labour, he would have too much to remain long in a low grade. The older economists, in constant contact as they were with the actual facts of business life, must have known this well enough; but partly for brevity and simplicity, partly because the term "free competition" had become almost a catchword, partly because they had not sufficiently classified and conditioned their doctrines, they often seemed to imply that they did assume this perfect knowledge."

One of Marshall's diagrams for monopoly: DD' is the demand curve, SS' the supply curve, QQ' is the monopoly revenue curve and q3 the maximum revenue point. Cournot had already considered the mathematics of monopoly in the Mathematical Principles of the Theory of Wealth but he draw no diagram

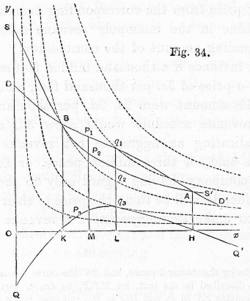
Marshall also discussed how income affects consumption:

"The substance of our argument would not be affected if we took account of the fact that, the more a person spends on anything the less power he retains of purchasing more of it or of other things, and the greater is the value of money to him (in technical language every fresh expenditure increases the marginal value of money to him). But though its substance would not be altered, its form would be made more intricate without any corresponding gain; for there are very few practical problems, in which the corrections to be made under this head would be of any importance. There are however some exceptions. For instance, as Sir R. Giffen has pointed out, a rise in the price of bread makes so large a drain on the resources of the poorer labouring families and raises so much the marginal utility of money to them, that they are forced to curtail their consumption of meat and the more expensive farinaceous foods: and, bread being still the cheapest food which they can get and will take, they consume more, and not less of it. But such cases are rare; when they are met with, each must be treated on its own merits."

This exception is called in microeconomics textbooks the consumption of a Giffen Good.

Production and costs

An early formulation of the concept of production functions is due to Johann Heinrich von Thünen, which presented an exponential version of it. The standard Cobb–Douglas production function found in microeconomics textbooks refers to a collaborative paper between Charles Cobb and Paul Douglas published in 1928 in which they analyzed U.S. manufacturing data (1899-1922) using this function as the basis of a regression analysis for estimating the relationship between inputs (labour and capital) and output (product), discussing the problem using the concept of marginal productivity, the authors concluded:

"In closing, it should be made clear that we do not claim to have actually solved the law of production, but merey that we have made an approximation to it and suggested a method of attack. Future progress wil be assisted by developing more refined series, by using different mathematical techniques, and by analyzing other sets of data."

The mathematical form of the Cobb–Douglas function can be found in the prior work of Wicksell, Thünen, and Turgot.

Cost curves as a function of output: the long run average cost (LRAC) given as the envelope of short run average total costs (ARC) minimums.

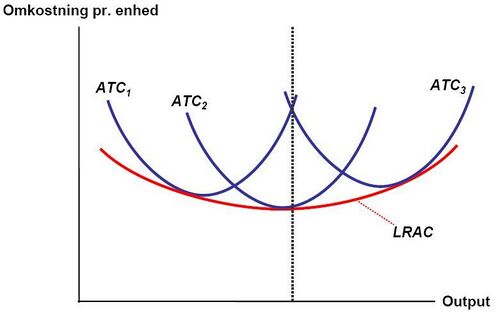
Jacob Viner presented an early procedure for constructing cost curves in his "Cost Curves and Supply Curves" (1931), the paper was an attempt to reconcile two streams of thought when dealing with this issue at the time: the idea that supplies of factors of production were given and independent of rate of remuneration (Austrian School) or dependent on rate of remuneration (English School, that is followers of Marshall). Viner argued that, "The differences between the two schools would not affect qualitatively the character of the findings," more specifically, "...that this concern is not of sufficient importance to bring about any change in the prices of the factors as a result of a change in its output."

In Viner's terminology—now considered standard—the short run is a period long enough to permit any desired output change that is technologically possible without altering the scale of the plant—but is not long enough to adjust the scale of the plant. He arbitrarily assumes that all factors can, for the short run, be classified in two groups: those necessarily fixed in amount, and those freely variable. Scale of plant is the size of the group of factors that are fixed in amount in the short-run, and each scale is quantitatively indicated by the amount of output that can be produced at the lowest average cost possible at that scale. Costs associated with the fixed factors are fixed costs. Those associated with the variable factors are direct costs. Note that fixed costs are fixed only in their aggregate amounts, and vary with output in their amount per unit, while direct costs vary in their aggregate amount as output varies, as well as in their amount per unit. The spreading of overhead is therefore a short-run phenomenon and not to be confused with the long-run.

He explains that if the law of diminishing returns holds that output per unit of variable factor falls as total output rises, and that if the prices of the factors remain constant—then average direct costs increase with output. Also, if atomistic competition prevails—that is, the individual firm output won't affect product prices—then the individual firm short-run supply curve equals the short run marginal cost curve. In the long run, the supply curve for industry can be constructed by summing individual marginal cost curves abscissas. He also explains that:

• Internal economies of scale are primarily a long-run phenomenon and are due either to reductions in the technical coefficients of production (technical economies=increasing productivity by improved organisation or methods of production) or to discounts resulting from larger size (pecuniary economies).
• Internal diseconomies of scale can be avoided by increasing industry output by increasing the number of plants without increasing the scale of the plant.
• External economies of scale are also either technical or pecuniary, but in this case are due to the aggregate behaviour of the industry, and refer to the size of output of the industry as a whole.
• External diseconomies of scale may occur if as industry output rises the unit price of factors and materials rises as well due to increasing competition for inputs with other industries.

It should be made clear that these long-run results only hold if producer are rational actors, that is able to optimise their production so as to have an optimal scale of plant.

Imperfect competition and game theory

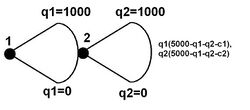
In 1929 Harold Hotelling published "Stability in Competition" addressing the problem of instability in the classic Cournout model: Bertrand criticized it for lacking equilibrium for prices as independent variables and Edgeworth constructed a dual monopoly model with correlated demand with also lacked stability. Hotteling proposed that demand typically varied continuously for relative prices, not discontinuously as suggested by the later authors.

Following Sraffa he argued for "the existence with reference to each seller of groups who will deal with him instead of his competitors in spite of difference in price", he also noticed that traditional models that presumed the uniqueness of price in the market only made sense if the commodity was standardized and the market was a point: akin to a temperature model in physics, discontinuity in heat transfer (price changes) inside a body (market) would lead to instability. To show the point he built a model of market located over a line with two sellers in each extreme of the line, in this case maximizing profit for both sellers leads to a stable equilibrium. From this model also follows that if a seller is to choose the location of his store so as to maximize his profit, he will place his store the closest to his competitor: "the sharper competition with his rival is offset by the greater number of buyers he has an advantage". He also argues that clustering of stores is wasteful from the point of view of transportation costs and that public interest would dictate more spatial dispersion.

A new impetus was given to the field when Edward H. Chamberlin and Joan Robinson, published respectively, The Theory of Monopolistic Competition (1923) and The Economics of Imperfect Competition (1933), introducing models of imperfect competition. Although the monopoly case was already exposed in Marshall's Principles of Economics and Cournot had already constructed models of duopoly and monopoly in 1838, a whole new set of models grew out of this new literature. In particular the monopolistic competition model results in a non efficient equilibrium. Chamberlin defined monopolistic competition as, "...challenge to traditional viewpoint of economics that competition and monopoly are alternatives and that individual prices are to be explained in terms of one or the other." He continues, "By contrast it is held that most economic situations are composite of both competition and monopoly, and that, wherever this is the case, a false view is given by neglecting either one of the two forces and regarding the situation as made up entirely of the other."

Game theory and dynamic adjustments

Cobweb model with stable equilibrium.

Cobweb model with unstable equilibrium.

Later, some market models were built using game theory, particularly regarding oligopolies, which was being developed by John von Neumann at least from 1928. Game theory was originally applied to le Her and chess, both sequential games, economics as developed by Alfred Marshall on other hand, while adopting the Cartesian coordinate system, considered only static games. This may seem counterintuitive since Marshall considered that economic behavior might change in the long run and that "an equilibrium is stable; that is, the price, if displaced a little from it, will tend to return, as a pendulum oscillates about its lowest point", Nicholas Kaldor was aware of this problem: economic equilibrium is not always stable and not always unique since it depends on the shapes of both the demand curve and the supply curve, he explained the situation in 1934 as follows:

"We shall examine these objections in turn by enumerating, in each case, the conditions which are necessary to make them inoperative( or in the absence of which they would be operative). We shall call an equilibrium "determinate" or "indeterminate" according as the final position is independent of the route followed, or not; we shall call equilibrium "unique" or "multiple" according as there is one, or more than one, system of equilibrium-prices, corresponding to a given set of data; and, finally, we shall speak of "definite" or "indefinite" equilibria, according the actual situation tends to approximate a position of equilibrium or not."

Regarding price adjustments, he said:

"Finally, we have to take account of the fact that adjustments always proceed at more or less frequent intervals-that they are more or less continuous. The quantity of anything demanded or supplied may change once a Day, once a week, a month, or a year-depending on such factors as the technical period of production, etc. We shall call an adjustment completely discontinuous, if the full quantitative adjustment to a given price-change occurs all at once, at the end of a certain period. (E.g. a change in the price of rubber may not influence the rate of supply for a period of seven years, at the end of which the full quantitative reaction may take place at once. Or a change in the price of corn, by inducing farmers to change the area sown, will make its effect felt a year later when the new harvest comes to the market.) Similarly, we shall call an adjustment completely continuous, if it proceeds at a steady rate in time, or if the time-lags between the appearance of successive quantitative changes are such as can be neglected. The latter will always be the case when the degree of discontinuity-the length of the "time-lags"-is the same on the demand side as on the supply side. In the following analysis we shall treat only these two cases of complete discontinuity and continuity."

Stackelberg competition represented as an extensive form game with infinite action space, the players payoffs are on the right.

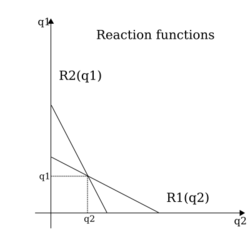
A good example of how microeconomics started to incorporate game theory, is the Stackelberg competition model published in that same year of 1934, which can be characterised as a dynamic game with a leader and a follower, and then be solved to find a Nash Equilibrium, named after John Nash who gave a very general definition of it. Von Neumann's work culminated in the 1944 book Theory of Games and Economic Behavior, which was cowriten with Oskar Morgenstern. Regarding the use of mathematics in economics, the authors had this to say:

"It may be opportune to begin with some remarks concerning the nature of economic theory and to discuss briefly the question of the role which mathematics may take in its development. First let us be aware that there exists at present no universal system of economic theory and that, if one should ever be developed, it will very probably not be during our lifetime. The reason for this is simply that economics is far too difficult a science to permit its construction rapidly, especially in view of the very limited knowledge and imperfect description of the facts with which economists are dealing. Only those wlio fail to appreciate this condition are likely to attempt the construction of universal systems. Even in sciences which are far more advanced than economics, like physics, there is no universal system available at present."

A major problem discussed in this book if that of rational behavior under strategic situations involving other participants:

"First, the "rules of the game," i.e. the physical laws which give the factual background of the economic activities under consideration may be explicitly statistical. The actions of the participants of the economy may determine the outcome only in conjunction with events which depend on chance (with known probabilities), cf. footnote 2 on p. 10 and 6.2.1. If this is taken into consideration, then the rules of behavior even in a perfectly rational community must provide for a great variety of situations some of which will be very far from optimum.

Second, and this is even more fundamental, the rules of rational behavior must provide definitely for the possibility of irrational conduct on the part of others. In other words: Imagine that we have discovered a set of rules for all participants to be termed as "optimal" or "rational" each of which is indeed optimal provided that the other participants conform. Then the question remains as to what will happen if some of the participants do not conform. If that should turn out to be advantageous for them and, quite particularly, disadvantageous to the conformists then the above "solution" would seem very questionable. We are in no position to give a positive discussion of these things as yet but we want to make it clear that under such conditions the "solution," or at least its motivation, must be considered as imperfect and incomplete. In whatever way we formulate the guiding principles and the objective justification of "rational behavior," provisos will have to be made for every possible conduct of "the others." Only in this way can a satisfactory and exhaustive theory be developed. But if the superiority of "rational behavior" over any other kind is to be established, then its description must include rules of conduct for all conceivable situations including those where "the others" behaved irrationally, in the sense of the standards which the theory will set for them.

At this stage the reader will observe a great similarity with the everyday concept of games. We think that this similarity is very essential; indeed, that it is more than that. For economic and social problems the games fulfill or should fulfill the same function which various geometrico-mathematical models have successfully performed in the physical sciences. Such models are theoretical constructs with a precise, exhaustive and not too complicated definition; and they must be similar to reality in those respects which are essential in the investigation at hand. To recapitulate in detail: The definition must be precise and exhaustive in order to make a mathematical treatment possible. The construct must not be unduly complicated, so that the mathematical treatment can be brought beyond the mere formalism to the point where it yields complete numerical results. Similarity to reality is needed to make the operation significant. And this similarity must usually be restricted to a few traits deemed "essential" pro tempore since otherwise the above requirements would conflict with each other.

It is clear that if a model of economic activities is constructed according to these principles, the description of a game results. This is particularly striking in the formal description of markets which are after all the core of the economic system but this statement is true in all cases and without qualifications."

Game theory considers very general types of payoffs, therefore Von Neumann and Morgestein defined the axioms necessary for rational behavior using utility;

Barriers to entry

William Baumol provided in his 1977 paper the current formal definition of a natural monopoly where "an industry in which multiform production is more costly than production by a monopoly" (p. 810): mathematically this equivalent to subadditivity of the cost function. He then sets out to prove 12 propositions related to strict economies of scale, ray average costs, ray concavity and transray convexity: in particular strictly declining ray average cost implies strict declining ray subadditivity, global economies of scale are sufficient but not necessary for strict ray subadditivity.

In 1982 paper Baumol defined a contestable market as a market where "entry is absolutely free and exit absolutely costless", freedom of entry in Stigler sense: the incumbent has no cost discrimination against entrants. He states that a contestable market will never have an economic profit greater than zero when in equilibrium and the equilibrium will also be efficient. According to Baumol this equilibrium emerges endogenously due to the nature of contestable markets, that is the only industry structure that survives in the long run is the one which minimizes total costs. This is in contrast to the older theory of industry structure since not only industry structure is not exogenously given, but equilibrium is reached without add hoc hypothesis on the behaviour of firms, say using reaction functions in a duopoly. He concludes the paper commenting that regulators that seek to impede entry and/or exit of firms would do better to not interfere if the market in question resembles a contestable market.

Externalities and market failure

Ronald Coase analyzed transaction costs, externalities and is also remembered for the Coase conjecture.

In 1937, "The Nature of the Firm" was published by Coase introducing the notion of transaction costs (the term itself was coined in the fifties), which explained why firms have an advantage over a group of independent contractors working with each other. The idea was that there were transaction costs in the use of the market: search and information costs, bargaining costs, etc., which give an advantage to a firm that can internalise the production process required to deliver a certain good to the market. A related result was published by Coase in his "The Problem of Social Cost" (1960), which analyses solutions of the problem of externalities through bargaining, in which he first describes a cattle herd invading a farmer's crop and then discusses four legal cases: Sturges v Bridgman (externality: machinery vibration), Cooke v Forbes (externality: fumes from ammonium sulfate), Bryant v Lejever (externality: chimney smoke), and Bass v Gregory (externality: brewery ventilation shaft). He then states:

"In earlier sections, when dealing with the problem of rearrangement of legal rights through the market, it was argued that such a rearrangement would be made through the market whenever this would lead to an increase in the value of production. But this assumed costless market transactions. Once the costs of carrying out market transactions are taken into account it is clear that such rearrangement of rights will only be undertaken when the increase in the value of production consequent upon the rearrangement is greater than the costs which would be involved in bringing it about. When it is less, the granting of an injunction (or the knowledge that it would be granted) or the liability to pay damages may result in an activity being discontinued (or may prevent its being started) which would be undertaken if market transactions were costless. In these conditions the initial delimitation of legal rights does have an effect on the efficiency with which the economic system operates. One arrangement of rights may bring about a greater value of production than any other. But unless this is the arrangement of rights established by the legal system, the costs of reaching the same result by altering and combining rights through the market may be so great that this optimal arrangement of rights, and the greater value of production which it would bring, may never be achieved."

This then becomes relevant in context of regulations. He argues against the Pigovian tradition:

"...The problem which we face in dealing with actions which have harmful effects is not simply one of restraining those responsible for them. What has to be decided is whether the gain from preventing the harm is greater than the loss which would be suffered elsewhere as a result of stopping the action which produces the harm. In a world in which there are costs of rearranging the rights established by the legal system, the courts, in cases relating to nuisance, are, in effect, making a decision on the economic problem and determining how resources are to be employed. It was argued that the courts are conscious of this and that they often make, although not always in a very explicit fashion, a comparison between what would be gained and what lost by preventing actions which have harmful effects. But the delimitation of rights is also the result of statutory enactments. Here we also find evidence of an appreciation of the reciprocal nature of the problem. While statutory enactments add to the list of nuisances, action is also taken to legalise what would otherwise be nuisances under the common law. The kind of situation which economists are prone to consider as requiring Government action is, in fact, often the result of Government action. Such action is not necessarily unwise. But there is a real danger that extensive Government intervention in the economic system may lead to the protection of those responsible for harmful being carried too far."

Public goods

This period also marks the beginning of mathematical modelling of public goods with Samuelson's "The Pure Theory of Public Expenditure" (1954), in it he gives a set of equations for efficient provision of public goods (he called them collective consumption goods), now known as the Samuelson condition. He then gives a description of what is now called the free rider problem:

"However no decentralised pricing system can serve to determine optimally these levels of collective consumption. Other kinds of "voting" or "signalling" would have to be tried. But, and this is the point sensed by Wicksell but perhaps not fully appreciated by Lindahl, now it is in the selfish interest of each person to give false signals, to pretend to have less interest in a given collective consumption activity than he has, etc."

Charles Tiebout considered the same problem as Samuelson and while agreeing with him at the federal level, proposed a different solution:

"Consider for a moment the case of the city resident about to move to the suburbs. What variables will influence his choice of a municipality? If he has children, a high level of expenditures on schools may be important. Another person may prefer a community with a municipal golf course. The availability and quality of such facilities and services as beaches, parks, police protection, roads, and parking facilities will enter into the decision-making process. Of course, non-economic variables will also be considered, but this is of no concern at this point. The consumer-voter may be viewed as picking that community which best satisfies his preference pattern for public goods. This is a major difference between central and local provision of public goods. At the central level the preferences of the consumer-voter are given, and the government tries to adjust to the pattern of these preferences, whereas at the local level various governments have their revenue and expenditure patterns more or less set." Given these revenue and expenditure patterns, the consumer-voter moves to that community whose local government best satisfies his set of preferences. The greater the number of communities and the greater the variance among them, the closer the consumer will come to fully realizing his preference position."

Used cars market: due to presence of fundamental asymmetrical information between seller and buyer the market equilibrium is not efficient; in the language of economists it is a market failure

Asymmetric Information

Around the 1970s the study of market failures again came into focus with the study of information asymmetry. In particular three authors emerged from this period: Akerlof, Spence, and Stiglitz. Akerlof considered the problem of bad quality cars driving good quality cars out of the market in his classic "The Market for Lemons" (1970) because of the presence of asymmetrical information between buyers and sellers. Spence explained that signaling was fundamental in the labour market, because since employers can't know beforehand which candidate is the most productive, a college degree becomes a signaling device that a firm uses to select new personnel. A synthesising paper of this era is "Externalities in Economies with Imperfect Information and Incomplete Markets" by Stiglitz and Greenwald: the basic model consists of households that maximise a utility function, firms that maximise profit—and a government that produces nothing, collects taxes, and distributes the proceeds. An initial equilibrium with no taxes is assumed to exist, a vector x of household consumption and vector z of other variables that affect household utilities (externalities) are defined, a vector π of profits is defined along with a vector E of households expenditures. Since the envelope theorem holds, if the initial non taxed equilibrium is Pareto optimal then it follows that the dot products Π (between π and the time derivative of z) and B (between E and the time derivative of z) must equal each other. They state:

"Except in the special case (which is unlikely to hold generically) where Π and B exactly cancel each other out, the existence of these externalities will make the initial equilibrium inefficient and guarantee the existence of welfare-improving tax measures." (p. 237)

One application of this result is to the already mentioned Market for Lemons, which deals with adverse selection: households buy from a pool of goods with heterogeneous quality considering only average quality, since in general the equilibrium is not efficient, any tax that raises average quality is beneficial (in the sense of optimal taxation). Other applications were considered by the authors, such as tax distortions, signaling, screening, moral hazard in insurance, incomplete markets, queue rationing, unemployment and rationing equilibrium. The authors conclude:

"The paper thus casts a new light on the First Fundamental Theorem of Welfare Economics asserting the Pareto efficiency of competititve equilibrium. The theorem is an achievement because it identifies what in retrospect has turned out to be the singular set of circumstances under which the economy is Pareto efficient. There is not a complete set of markets; information in imperfect; the commodities sold in any market are not homogeneous in relevant respects; it is costly to ascertain differences among the items; individuals do not get paid on a piece rate basis; and there is an element of insurance (implicit or explicit) in almost all contractual arrangements, in labor, capital, and product markets. In virtually all markets there are important instances of signaling and screening. Individuals must search for the commodities that they wish to purchase, firms must search for the workers who the wish to hire, and workers must search for the firm for which they wish to work. We frequently arrive at a store only to find that it is out of inventory; or at other times we arrive, to find a queue waiting to be served. Each of these are "small" instances, but their cumulative effects may indeed be large." (p. 259)

Behavioural economics

Asymmetric value function in prospect theory: big losses have a much bigger psychological impact than big gains

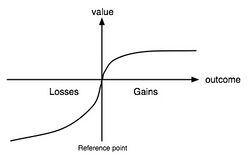
Kahneman and Tversky published a paper in 1979 criticising expected utility hypothesis and the very idea of the rational economic agent. The main point is that there is an asymmetry in the psychology of the economic agent that gives a much higher value to losses than to gains. This article is usually regarded as the beginning of behavioural economics and has consequences particularly regarding the world of finance. The authors summed the idea in the abstract as follows:

"...In particular, people underweight outcomes that are merely probable in comparison with outcomes that are obtained with certainty. This tendency, called certainty effect, contributes to risk aversion in choices involving sure gains and to risk seeking in choices involving sure losses. In addition, people generally discard components that are shared by all prospects under consideration. This tendency, called the isolation effect, leads to inconsistent preferences when the same choice is presented in different forms."

The paper deals also with the reflection effect, concerning risk seeking and risk aversion.

Great Recession and executive compensation

More recently, the Great Recession and the ongoing controversy on executive compensation brought the principal–agent problem again to the centre of debate, in particular regarding corporate governance and problems with incentive structures.

Further reading

• Bade, Robin; Michael Parkin (2001). Foundations of Microeconomics. Addison Wesley Paperback 1st Edition. 
• Bouman, John: Principles of Microeconomics – free fully comprehensive Principles of Microeconomics and Macroeconomics texts. Columbia, Maryland, 2011
• Colander, David. Microeconomics. McGraw-Hill Paperback, 7th Edition: 2008.
• Dunne, Timothy; J. Bradford Jensen; Mark J. Roberts (2009). Producer Dynamics: New Evidence from Micro Data. University of Chicago Press. ISBN 978-0-226-17256-9. 
• Eaton, B. Curtis; Eaton, Diane F.; and Douglas W. Allen. Microeconomics. Prentice Hall, 5th Edition: 2002.
• Frank, Robert H.; Microeconomics and Behavior. McGraw-Hill/Irwin, 6th Edition: 2006.
• Friedman, Milton. Price Theory. Aldine Transaction: 1976
• Hagendorf, Klaus: Labour Values and the Theory of the Firm. Part I: The Competitive Firm. Paris: EURODOS; 2009.
• Hicks, John R. Value and Capital. Clarendon Press. [1939] 1946, 2nd ed.
• Hirshleifer, Jack., Glazer, Amihai, and Hirshleifer, David, Price theory and applications: Decisions, markets, and information. Cambridge University Press, 7th Edition: 2005.
• Jehle, Geoffrey A.; and Philip J. Reny. Advanced Microeconomic Theory. Addison Wesley Paperback, 2nd Edition: 2000.
• Katz, Michael L.; and Harvey S. Rosen. Microeconomics. McGraw-Hill/Irwin, 3rd Edition: 1997.
• Kreps, David M. A Course in Microeconomic Theory. Princeton University Press: 1990
• Landsburg, Steven. Price Theory and Applications. South-Western College Pub, 5th Edition: 2001.
• Mankiw, N. Gregory. Principles of Microeconomics. South-Western Pub, 2nd Edition: 2000.
• Mas-Colell, Andreu; Whinston, Michael D.; and Jerry R. Green. Microeconomic Theory. Oxford University Press, US: 1995.
• McGuigan, James R.; Moyer, R. Charles; and Frederick H. Harris. Managerial Economics: Applications, Strategy and Tactics. South-Western Educational Publishing, 9th Edition: 2001.
• Nicholson, Walter. Microeconomic Theory: Basic Principles and Extensions. South-Western College Pub, 8th Edition: 2001.
• Perloff, Jeffrey M. Microeconomics. Pearson – Addison Wesley, 4th Edition: 2007.
• Perloff, Jeffrey M. Microeconomics: Theory and Applications with Calculus. Pearson – Addison Wesley, 1st Edition: 2007
• Pindyck, Robert S.; and Daniel L. Rubinfeld. Microeconomics. Prentice Hall, 7th Edition: 2008.
• Ruffin, Roy J.; and Paul R. Gregory. Principles of Microeconomics. Addison Wesley, 7th Edition: 2000.
• Varian, Hal R. (1987). "microeconomics," The New Palgrave: A Dictionary of Economics, v. 3, pp. 461–63.
• Varian, Hal R. Intermediate Microeconomics: A Modern Approach. W. W. Norton & Company, 8th Edition: 2009.
• Varian, Hal R. Microeconomic Analysis. W. W. Norton & Company, 3rd Edition: 1992.

External links

• http://media.lanecc.edu/users/martinezp/201/MicroHistory.html – a brief history of microeconomics

Podcasts and videos

• Related Nobel Prize lecture videos and other material
  • George Akerlof, Michael Spence, and Joseph Stiglitz (2001) "Analyses of markets with asymmetric information".
  • Daniel Kahneman (2002) "for having integrated insights from psychological research into economic science, especially concerning human judgment and decision-making under uncertainty" and Vernon L. Smith (2002) "for having established laboratory experiments as a tool in empirical economic analysis, especially in the study of alternative market mechanisms."