Infinite skew polygon
In geometry, an infinite skew polygon or skew apeirogon is an infinite 2-polytope has vertices that are not all colinear. Infinite zig-zag skew polygons are 2-dimensional infinite skew polygons with vertices alternating between two parallel lines. Infinite helical polygons are 3-dimensional infinite skew polygons with vertices on the surface of a cylinder.
Regular infinite skew polygons exist in the Petrie polygons of the affine and hyperbolic Coxeter groups. They are constructed a single operator as the composite of all the reflections of the Coxeter group.
Regular infinite skew polygons in two dimensions
| Infinite regular skew zig-zag polygon | |
|---|---|
 | |
| Edges and vertices | ∞ |
| Schläfli symbol | {∞}#{ } |
| Symmetry group | D∞d, [2+,∞], (2*∞) |

A regular skew zig-zag apeirogon has 2*∞, D∞d Frieze group symmetry.
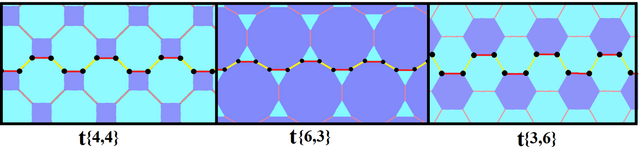
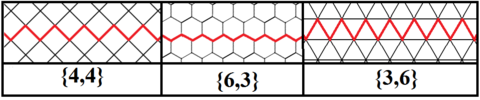
The infinite zig-zag regular skew polygons exists as Petrie polygons of the three regular tilings of the plane: {4,4}, {6,3}, and {3,6}. These infinite polygons have internal angles of 90°, 120°, and 60°, respectively, from the regular polygons within the tilings.
|
Isogonal infinite skew polygons
An infinite skew isogonal polygon alternates two types of edges with various Frieze group symmetries. Distorted infinite regular skew polygons produce zig-zagging isogonal ones with translational symmetry.
| p1, [∞]+, (∞∞), C∞ | |
|---|---|
 
|
 
|
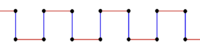
Other isogonal skew aperigons have alternate edges parallel to the frieze direction. These all have vertical mirror symmetry in the midpoints of the parallel edges. If both edges are the same length, they can be called quasiregular.
| p2mg, [2+,∞], (2*∞), D∞d | ||
|---|---|---|
 |
||
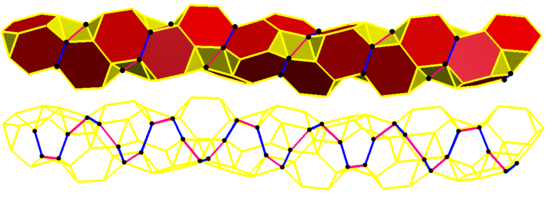
Example quasiregular skew apeirogons can be seen in the Euclidean tilings as truncated Petrie polygons in truncated regular tilings:
Hyperbolic skew apeirogons
In hyperbolic geometry, infinite regular skew polygons are similarly found like in the Euclidean plane.
Hyperbolic infinite regular skew polygons also exist as Petrie polygon zig-zagging edge paths on all of the regular tilings of the hyperbolic plane. And again like Euclidean space, hyperbolic infinite quasiregular skew polygons can be constructed as truncated petrie polygons within the edges of a truncated regular tiling.
| {3,7} | t{3,7} |
|---|---|
 Regular skew |
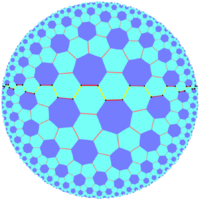 Quasiregular skew |
Infinite helical polygons in 3-dimensions
{∞} # {3}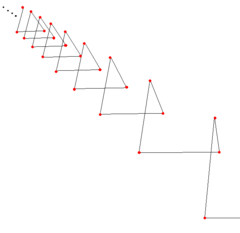 A regular helical skew polygon (drawn in perspective) |
An infinite helical skew polygon can exist in three dimensions, where the vertices can be seen as limited to the surface of a cylinder. The sketch on the right is a 3D perspective view of such a regular infinite helical polygon.
This infinite polygon can be most seen as constructed from the vertices in an infinite stack of uniform n-gonal uniform prisms or antiprisms, although in general the twist angle is not limited to an integer divisor of 180°. An infinite helical skew polygon has screw axis symmetry.
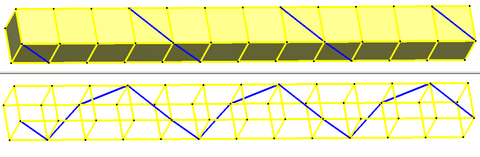
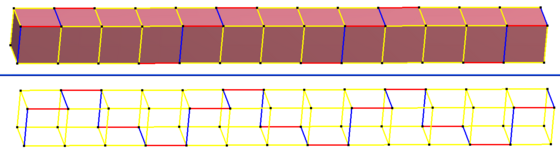
An infinite stack of prisms, for example cubes, contain an infinite helical polygon across the diagonals of the square faces, with a twist angle of 90° and can be represented as {∞} # {4}.
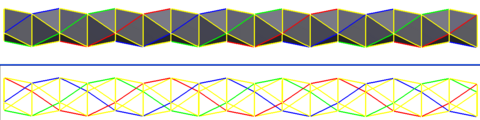
An infinite stack of antiprisms, for example octahedra, makes infinite helical polyongs, 3 here highlighted in red, green and blue, each with a twist angle of 60° and can be represented as {∞} # {6}.
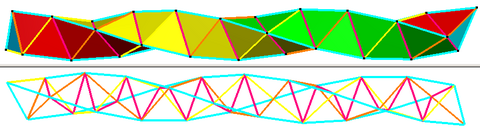
A sequence of edges of a Boerdijk–Coxeter helix can represent infinite regular helical polygons with an irrational twist angle:
Infinite isogonal helical polygons
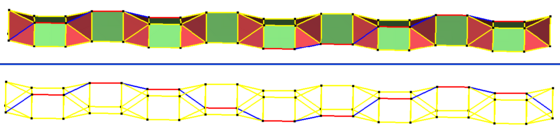
A stack of right prisms can generate isogonal helical aperigon alternating edges around axis, and along axis, here for example with square prisms, alternating red and blue edges:
Similarly an alternating stack of prisms and antiprisms can produce an infinite isogonal helical polygon, here for example, a triangular one with one shown:
An infinite isogonal helical polygon with an irrational twist angle can also be constructed from truncated tetrahedra stacked like a Boerdijk–Coxeter helix, alternating two types of edges, between pairs of hexagonal and pairs of triangular faces:
References
- Coxeter, H.S.M.; Regular complex polytopes (1974). Chapter 1. Regular polygons, 1.5. Regular polygons in n dimensions, 1.7. Zigzag and antiprismatic polygons, 1.8. Helical polygons. 4.3. Flags and Orthoschemes, 11.3. Petrie polygons