Vector calculus identities
This article includes a list of references, but its sources remain unclear because it has insufficient inline citations. (August 2017) (Learn how and when to remove this template message) |
| Part of a series of articles about |
| Calculus |
|---|
The following are important identities involving derivatives and integrals in vector calculus.
Operator notation
Gradient
For a function in three-dimensional Cartesian coordinate variables, the gradient is the vector field: where i, j, k are the standard unit vectors for the x, y, z-axes. More generally, for a function of n variables , also called a scalar field, the gradient is the vector field: where are mutually orthogonal unit vectors.
As the name implies, the gradient is proportional to, and points in the direction of, the function's most rapid (positive) change.
For a vector field , also called a tensor field of order 1, the gradient or total derivative is the n × n Jacobian matrix:[1]
For a tensor field of any order k, the gradient is a tensor field of order k + 1.
For a tensor field of order k > 0, the tensor field of order k + 1 is defined by the recursive relation where is an arbitrary constant vector.
Divergence
In Cartesian coordinates, the divergence of a continuously differentiable vector field is the scalar-valued function:
As the name implies, the divergence is a (local) measure of the degree to which vectors in the field diverge.
The divergence of a tensor field of non-zero order k is written as , a contraction of a tensor field of order k − 1. Specifically, the divergence of a vector is a scalar. The divergence of a higher-order tensor field may be found by decomposing the tensor field into a sum of outer products and using the identity, where is the directional derivative in the direction of multiplied by its magnitude. Specifically, for the outer product of two vectors,[2]
For a tensor field of order k > 1, the tensor field of order k − 1 is defined by the recursive relation where is an arbitrary constant vector.
Curl
In Cartesian coordinates, for the curl is the vector field: where i, j, and k are the unit vectors for the x-, y-, and z-axes, respectively.
As the name implies the curl is a measure of how much nearby vectors tend in a circular direction.
In Einstein notation, the vector field has curl given by: where = ±1 or 0 is the Levi-Civita parity symbol.
For a tensor field of order k > 1, the tensor field of order k is defined by the recursive relation where is an arbitrary constant vector.
A tensor field of order greater than one may be decomposed into a sum of outer products, and then the following identity may be used: Specifically, for the outer product of two vectors,[3]
Laplacian
In Cartesian coordinates, the Laplacian of a function is
The Laplacian is a measure of how much a function is changing over a small sphere centered at the point.
When the Laplacian is equal to 0, the function is called a harmonic function. That is,
For a tensor field, , the Laplacian is generally written as: and is a tensor field of the same order.
For a tensor field of order k > 0, the tensor field of order k is defined by the recursive relation where is an arbitrary constant vector.
Special notations
In Feynman subscript notation, where the notation ∇B means the subscripted gradient operates on only the factor B.[4][5][6]
More general but similar is the Hestenes overdot notation in geometric algebra.[7][8] The above identity is then expressed as: where overdots define the scope of the vector derivative. The dotted vector, in this case B, is differentiated, while the (undotted) A is held constant.
The utility of the Feynman subscript notation lies in its use in the derivation of vector and tensor derivative identities, as in the following example which uses the algebraic identity C⋅(A×B) = (C×A)⋅B:
An alternative method is to use the Cartesian components of the del operator as follows (with implicit summation over the index i):
Another method of deriving vector and tensor derivative identities is to replace all occurrences of a vector in an algebraic identity by the del operator, provided that no variable occurs both inside and outside the scope of an operator or both inside the scope of one operator in a term and outside the scope of another operator in the same term (i.e., the operators must be nested). The validity of this rule follows from the validity of the Feynman method, for one may always substitute a subscripted del and then immediately drop the subscript under the condition of the rule. For example, from the identity A⋅(B×C) = (A×B)⋅C we may derive A⋅(∇×C) = (A×∇)⋅C but not ∇⋅(B×C) = (∇×B)⋅C, nor from A⋅(B×A) = 0 may we derive A⋅(∇×A) = 0. On the other hand, a subscripted del operates on all occurrences of the subscript in the term, so that A⋅(∇A×A) = ∇A⋅(A×A) = ∇⋅(A×A) = 0. Also, from A×(A×C) = A(A⋅C) − (A⋅A)C we may derive ∇×(∇×C) = ∇(∇⋅C) − ∇2C, but from (Aψ)⋅(Aφ) = (A⋅A)(ψφ) we may not derive (∇ψ)⋅(∇φ) = ∇2(ψφ).
A subscript c on a quantity indicates that it is temporarily considered to be a constant. Since a constant is not a variable, when the substitution rule (see the preceding paragraph) is used it, unlike a variable, may be moved into or out of the scope of a del operator, as in the following example:[9]
Another way to indicate that a quantity is a constant is to affix it as a subscript to the scope of a del operator, as follows:[10]
For the remainder of this article, Feynman subscript notation will be used where appropriate.
First derivative identities
For scalar fields , and vector fields , , we have the following derivative identities.
Distributive properties
First derivative associative properties
Product rule for multiplication by a scalar
We have the following generalizations of the product rule in single-variable calculus.
Quotient rule for division by a scalar
Chain rule
Let be a one-variable function from scalars to scalars, a parametrized curve, a function from vectors to scalars, and a vector field. We have the following special cases of the multi-variable chain rule.
For a vector transformation we have:
Here we take the trace of the dot product of two second-order tensors, which corresponds to the product of their matrices.
Dot product rule
where denotes the Jacobian matrix of the vector field .
Alternatively, using Feynman subscript notation,
See these notes.[11]
As a special case, when A = B,
The generalization of the dot product formula to Riemannian manifolds is a defining property of a Riemannian connection, which differentiates a vector field to give a vector-valued 1-form.
Cross product rule
Note that the matrix is antisymmetric.
Second derivative identities
Divergence of curl is zero
The divergence of the curl of any continuously twice-differentiable vector field A is always zero:
This is a special case of the vanishing of the square of the exterior derivative in the De Rham chain complex.
Divergence of gradient is Laplacian
The Laplacian of a scalar field is the divergence of its gradient: The result is a scalar quantity.
Divergence of divergence is not defined
The divergence of a vector field A is a scalar, and the divergence of a scalar quantity is undefined. Therefore,
Curl of gradient is zero
The curl of the gradient of any continuously twice-differentiable scalar field (i.e., differentiability class ) is always the zero vector:
It can be easily proved by expressing in a Cartesian coordinate system with Schwarz's theorem (also called Clairaut's theorem on equality of mixed partials). This result is a special case of the vanishing of the square of the exterior derivative in the De Rham chain complex.
Curl of curl
Here ∇2 is the vector Laplacian operating on the vector field A.
Curl of divergence is not defined
The divergence of a vector field A is a scalar, and the curl of a scalar quantity is undefined. Therefore,
Second derivative associative properties
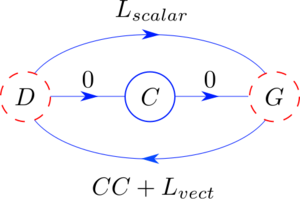
A mnemonic
The figure to the right is a mnemonic for some of these identities. The abbreviations used are:
- D: divergence,
- C: curl,
- G: gradient,
- L: Laplacian,
- CC: curl of curl.
Each arrow is labeled with the result of an identity, specifically, the result of applying the operator at the arrow's tail to the operator at its head. The blue circle in the middle means curl of curl exists, whereas the other two red circles (dashed) mean that DD and GG do not exist.
Summary of important identities
Differentiation
Gradient
Divergence
Curl
Vector-dot-Del Operator
Second derivatives
Third derivatives
Integration
Below, the curly symbol ∂ means "boundary of" a surface or solid.
Surface–volume integrals
In the following surface–volume integral theorems, V denotes a three-dimensional volume with a corresponding two-dimensional boundary S = ∂V (a closed surface):
-
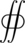
-
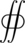 (divergence theorem)
(divergence theorem) -
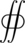
-
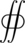 (Green's first identity)
(Green's first identity) -
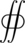
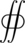 (Green's second identity)
(Green's second identity) -
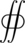 (integration by parts)
(integration by parts) -
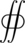 (integration by parts)
(integration by parts) -
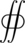 (integration by parts)
(integration by parts) -
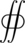 [14]
[14] -
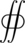 [15]
[15]
Curve–surface integrals
In the following curve–surface integral theorems, S denotes a 2d open surface with a corresponding 1d boundary C = ∂S (a closed curve):
Integration around a closed curve in the clockwise sense is the negative of the same line integral in the counterclockwise sense (analogous to interchanging the limits in a definite integral):
Endpoint-curve integrals
In the following endpoint–curve integral theorems, P denotes a 1d open path with signed 0d boundary points and integration along P is from to :
Tensor integrals
A tensor form of a vector integral theorem may be obtained by replacing the vector (or one of them) by a tensor, provided that the vector is first made to appear only as the right-most vector of each integrand. For example, Stokes' theorem becomes[18]
- .
A scalar field may also be treated as a vector and replaced by a vector or tensor. For example, Green's first identity becomes
-
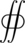 .
.
Similar rules apply to algebraic and differentiation formulas. For algebraic formulas one may alternatively use the left-most vector position.
See also
- Comparison of vector algebra and geometric algebra
- Del in cylindrical and spherical coordinates – Mathematical gradient operator in certain coordinate systems
- Differentiation rules – Rules for computing derivatives of functions
- Exterior calculus identities
- Exterior derivative – Operation on differential forms
- List of limits
- Vector algebra relations – Formulas about vectors in three-dimensional Euclidean space
References
- ↑ Wilson, p. 404.
- ↑ Wilson, p. 407.
- ↑ Wilson, p. 407.
- ↑ Coffin, Joseph George (1911). Vector Analysis. New York: John Wiley & Sons, Inc.. pp. 105–106, 120–123. https://books.google.com/books?id=9mgGAQAAIAAJ.
- ↑ Feynman, R. P.; Leighton, R. B.; Sands, M. (1964). The Feynman Lectures on Physics. Addison-Wesley. pp. Vol II, pp. 27–4, 5. ISBN 0-8053-9049-9. https://archive.org/details/the-feynman-lectures-on-physics-volume-2.
- ↑ Kholmetskii, A. L.; Missevitch, O. V. (2005). "The Faraday induction law in relativity theory". p. 4. arXiv:physics/0504223.
- ↑ Coffin, pp. 227–228.
- ↑ Doran, C.; Lasenby, A. (2003). Geometric algebra for physicists. Cambridge University Press. p. 169. ISBN 978-0-521-71595-9. https://archive.org/details/doran-lasenby-geometric-algebra-for-physicists-2003.
- ↑ Borisenko, A. I.; Tarapov, I. E. (1968). Vector and Tensor Analysis. New York: Dover Publications, Inc.. pp. 170, 180. https://archive.org/details/borisenko-tarapov-vector-and-tensor-analysis-with-applications.
- ↑ Wilson, Edwin Bidwell (1901). Vector Analysis. New York: Charles Scribner's Sons. pp. 159, 161–162. https://archive.org/details/0479777.0001.001.umich.edu.
- ↑ Kelly, P. (2013). "Chapter 1.14 Tensor Calculus 1: Tensor Fields". Mechanics Lecture Notes Part III: Foundations of Continuum Mechanics. University of Auckland. http://homepages.engineering.auckland.ac.nz/~pkel015/SolidMechanicsBooks/Part_III/Chapter_1_Vectors_Tensors/Vectors_Tensors_14_Tensor_Calculus.pdf. Retrieved 7 December 2017.
- ↑ "lecture15.pdf". https://www2.ph.ed.ac.uk/~mevans/mp2h/VTF/lecture15.pdf.
- ↑ Kuo, Kenneth K.; Acharya, Ragini (2012). Applications of turbulent and multi-phase combustion. Hoboken, N.J.: Wiley. p. 520. doi:10.1002/9781118127575.app1. ISBN 9781118127575. https://onlinelibrary.wiley.com/doi/pdf/10.1002/9781118127575.app1. Retrieved 19 April 2020.
- ↑ Page and Adams, pp. 65–66.
- ↑ Wangsness, Roald K.; Cloud, Michael J. (1986). Electromagnetic Fields (2nd ed.). Wiley. ISBN 978-0-471-81186-2.
- ↑ Page, Leigh; Adams, Norman Ilsley, Jr. (1940). Electrodynamics. New York: D. Van Nostrand Company, Inc.. pp. 44–45, Eq. (18-3). https://archive.org/details/in.ernet.dli.2015.523590.
- ↑ Pérez-Garrido, Antonio (2024). "Recovering seldom-used theorems of vector calculus and their application to problems of electromagnetism". American Journal of Physics 92 (5): 354–359. doi:10.1119/5.0182191. Bibcode: 2024AmJPh..92e.354P.
- ↑ Wilson, p. 409.
Further reading
- Balanis, Constantine A. (23 May 1989). Advanced Engineering Electromagnetics. ISBN 0-471-62194-3.
- Schey, H. M. (1997). Div Grad Curl and all that: An informal text on vector calculus. W. W. Norton & Company. ISBN 0-393-96997-5.
- Griffiths, David J. (1999). Introduction to Electrodynamics. Prentice Hall. ISBN 0-13-805326-X. https://archive.org/details/introductiontoel00grif_0.
 |
