Philosophy:Pseudomathematics
Pseudomathematics, or mathematical crankery, is a mathematics-like activity that does not adhere to the framework of rigor of formal mathematical practice. Common areas of pseudomathematics are solutions of problems proved to be unsolvable or recognized as extremely hard by experts, as well as attempts to apply mathematics to non-quantifiable areas. A person engaging in pseudomathematics is called a pseudomathematician or a pseudomath.[1] Pseudomathematics has equivalents in other scientific fields, and may overlap with other topics characterized as pseudoscience.
Pseudomathematics often contains mathematical fallacies whose executions are tied to elements of deceit rather than genuine, unsuccessful attempts at tackling a problem. Excessive pursuit of pseudomathematics can result in the practitioner being labelled a crank. Because it is based on non-mathematical principles, pseudomathematics is not related to misguided attempts at genuine proofs. Indeed, such mistakes are common in the careers of amateur mathematicians, some of whom go on to produce celebrated results.[1]
The topic of mathematical crankery has been extensively studied by mathematician Underwood Dudley, who has written several popular works about mathematical cranks and their ideas.
Examples
One common type of approach is claiming to have solved a classical problem that has been proved to be mathematically unsolvable. Common examples of this include the following constructions in Euclidean geometry—using only a compass and straightedge:
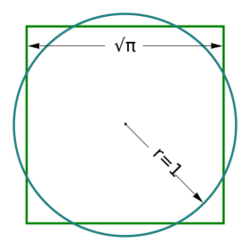
- Squaring the circle: Given any circle drawing a square having the same area.
- Doubling the cube: Given any cube drawing a cube with twice its volume.
- Trisecting the angle: Given any angle dividing it into three smaller angles all of the same size.[2][3][4]
For more than 2,000 years, many people had tried and failed to find such constructions; in the 19th century, they were all proven impossible.[5][6]:47
Another notable case were "Fermatists", who plagued mathematical institutions with requests to check their proofs of Fermat's Last Theorem.[7][8]
Another common approach is to misapprehend standard mathematical methods, and to insist that the use or knowledge of higher mathematics is somehow cheating or misleading (e.g., the denial of Cantor's diagonal argument[9]:40ff or Gödel's incompleteness theorems).[9]:167ff
History
The term pseudomath was coined by the logician Augustus De Morgan, discoverer of De Morgan's laws, in his A Budget of Paradoxes (1872). De Morgan wrote:
The pseudomath is a person who handles mathematics as the monkey handled the razor. The creature tried to shave himself as he had seen his master do; but, not having any notion of the angle at which the razor was to be held, he cut his own throat. He never tried a second time, poor animal! but the pseudomath keeps on at his work, proclaims himself clean-shaved, and all the rest of the world hairy.[10]
De Morgan named James Smith as an example of a pseudomath who claimed to have proved that π is exactly 3+1/8.[1] Of Smith, De Morgan wrote: "He is beyond a doubt the ablest head at unreasoning, and the greatest hand at writing it, of all who have tried in our day to attach their names to an error."[10] The term pseudomath was adopted later by Tobias Dantzig.[11] Dantzig observed:
With the advent of modern times, there was an unprecedented increase in pseudomathematical activity. During the 18th century, all scientific academies of Europe saw themselves besieged by circle-squarers, trisectors, duplicators, and perpetuum mobile designers, loudly clamoring for recognition of their epoch-making achievements. In the second half of that century, the nuisance had become so unbearable that, one by one, the academies were forced to discontinue the examination of the proposed solutions.[11]
The term pseudomathematics has been applied to attempts in mental and social sciences to quantify the effects of what is typically considered to be qualitative.[12] More recently, the same term has been applied to creationist attempts to refute the theory of evolution, by way of spurious arguments purportedly based in probability or complexity theory, such as intelligent design proponent William Dembski's concept of specified complexity.[13][14]
See also
- 0.999..., often fallaciously[15] claimed to be distinct from 1
- Indiana Pi Bill
- Eccentricity (behavior)
- Mathematical fallacy
- Pseudoscience
References
- ↑ 1.0 1.1 1.2 Lynch, Peter. "Maths discoveries by amateurs and distractions by cranks" (in en). The Irish Times. https://www.irishtimes.com/opinion/editorial/maths-discoveries-by-amateurs-and-distractions-by-cranks-1.3751301.
- ↑ Dudley, Underwood (1983). "What To Do When the Trisector Comes". The Mathematical Intelligencer 5 (1): 20–25. doi:10.1007/bf03023502. http://web.mst.edu/~lmhall/WhatToDoWhenTrisectorComes.pdf.
- ↑ Schaaf, William L. (1973). A Bibliography of Recreational Mathematics, Volume 3. National Council of Teachers of Mathematics. pp. 161. https://archive.org/stream/ERIC_ED087631#page/n173/mode/2up. "Pseudomath. A term coined by Augustus De Morgan to identify amateur or self-styled mathematicians, particularly circle-squarers, angle-trisectors, and cube-duplicators, although it can be extended to include those who deny the validity of non-Euclidean geometries. The typical pseudomath has but little mathematical training and insight, is not interested in the results of orthodox mathematics, has complete faith in his own capabilities, and resents the indifference of professional mathematicians."
- ↑ Johnson, George (1999-02-09). "Genius or Gibberish? The Strange World of the Math Crank". The New York Times. https://www.nytimes.com/1999/02/09/science/genius-or-gibberish-the-strange-world-of-the-math-crank.html.
- ↑ Wantzel, P M L (1837). "Recherches sur les moyens de reconnaître si un problème de Géométrie peut se résoudre avec la règle et le compas.". Journal de Mathématiques Pures et Appliquées. 1 2: 366–372.
- ↑ Bold, Benjamin (1982). Famous Problems of Geometry and How to Solve Them. Dover Publications. https://archive.org/details/famousproblemsof0000bold_e3s8.
- ↑ Konrad Jacobs, Invitation to Mathematics, 1992, p. 7
- ↑ Underwood Dudley, Mathematical Cranks 2019, p. 133
- ↑ 9.0 9.1 Dudley, Underwood (1992). Mathematical Cranks. Mathematical Association of America. ISBN 0-88385-507-0.
- ↑ 10.0 10.1 De Morgan, Augustus (1915). A Budget of Paradoxes (2nd ed.). Chicago: The Open Court Publishing Co.. https://www.gutenberg.org/files/26408/26408-h/26408-h.htm.
- ↑ 11.0 11.1 Dantzig, Tobias (1954). "The Pseudomath". The Scientific Monthly 79 (2): 113–117. Bibcode: 1954SciMo..79..113D.
- ↑ Johnson, H. M. (1936). "Pseudo-Mathematics in the Mental and Social Sciences". The American Journal of Psychology 48 (2): 342–351. doi:10.2307/1415754. ISSN 0002-9556.
- ↑ Elsberry, Wesley; Shallit, Jeffrey (2011). "Information theory, evolutionary computation, and Dembski's "complex specified information"". Synthese 178 (2): 237–270. doi:10.1007/s11229-009-9542-8.
- ↑ Rosenhouse, Jason (2001). "How Anti-Evolutionists Abuse Mathematics". The Mathematical Intelligencer 23: 3–8. http://educ.jmu.edu/~rosenhjd/sewell.pdf.
- ↑ "Why Does 0.999… = 1?". https://math.hmc.edu/funfacts/why-does-0-999-1/.
Further reading
- Underwood Dudley (1987), A Budget of Trisections, Springer Science+Business Media. ISBN 978-1-4612-6430-9. Revised and reissued in 1996 as The Trisectors, Mathematical Association of America. ISBN 0-88385-514-3.
- Underwood Dudley (1997), Numerology: Or, What Pythagoras Wrought, Mathematical Association of America. ISBN 0-88385-524-0.
- Clifford Pickover (1999), Strange Brains and Genius, Quill. ISBN 0-688-16894-9.
- Bailey, David H.; Borwein, Jonathan M.; de Prado, Marcos López; Zhu, Qiji Jim (2014). "Pseudo-Mathematics and Financial Charlatanism: The Effects of Backtest Overfitting on Out-of-Sample Performance". Notices of the AMS 61 (5): 458–471. doi:10.1090/noti1105. https://www.ams.org/notices/201405/rnoti-p458.pdf.
 |

