Physics:Endoreversible thermodynamics

Endoreversible thermodynamics is a subset of irreversible thermodynamics aimed at making more realistic assumptions about heat transfer than are typically made in reversible thermodynamics. It gives an upper bound on the power that can be derived from a real process that is lower than that predicted by Carnot for a Carnot cycle, and accommodates the exergy destruction occurring as heat is transferred irreversibly.

It is also called finite-time thermodynamics, entropy generation minimization, or thermodynamic optimization.

History

Endoreversible thermodynamics was discovered multiple times, with Reitlinger (1929), Novikov (1957) and Chambadal (1957), although it is most often attributed to Curzon & Ahlborn (1975).

Reitlinger derived it by considering a heat exchanger receiving heat from a finite hot stream fed by a combustion process.

A brief review of the history of rediscoveries is in.

Efficiency at maximal power

Novikov engine showing irreversible heat transfer between [math]\displaystyle{ T_H }[/math] and [math]\displaystyle{ T_{iH} }[/math], coupled to a Carnot cycle operating between [math]\displaystyle{ T_{iH} }[/math] and [math]\displaystyle{ T_C }[/math].

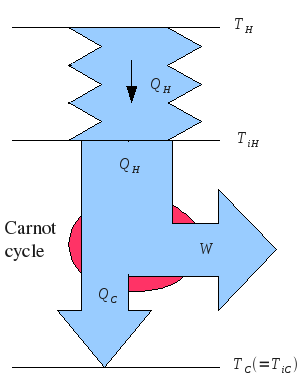
Consider a semi-ideal heat engine, in which heat transfer takes time, according to Fourier's law of heat conduction: [math]\displaystyle{ \dot Q \propto \Delta T }[/math], but other operations happen instantly.

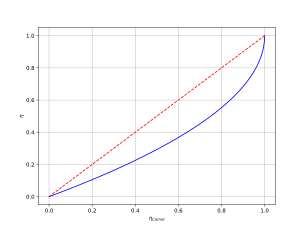
Its maximal efficiency is the standard Carnot result, but it requires heat transfer to be reversible (quasistatic), thus taking infinite time. At maximum power output, its efficiency is the Chambadal–Novikov efficiency:

[math]\displaystyle{ \eta = 1 - \sqrt{\frac{T_L}{T_H}} = 1-\sqrt{1-\eta_{Carnot} } }[/math]

Due to occasional confusion about the origins of the above equation, it is sometimes named the Chambadal–Novikov–Curzon–Ahlborn efficiency.

The plot of Chambadal–Novikov efficiency as a function of Carnot efficiency. We see that it is always less than Carnot efficiency, but approaches it at the two ends.

Derivation

This derivation is a slight simplification of Curzon & Ahlborn.

Consider a heat engine, with a single working fluid cycling around the engine. On one side, the working fluid has temperature [math]\displaystyle{ T_H' }[/math], and is in direct contact with the hot heat bath. On the other side, it has temperature [math]\displaystyle{ T_L' }[/math], and is in direct contact with the cold heat bath.

The heat flow into the engine is [math]\displaystyle{ \dot Q_H = k_H(T_H - T_H') }[/math], where [math]\displaystyle{ k_H }[/math] is the heat conduction coefficient. The heat flow out of the engine is [math]\displaystyle{ \dot Q_L = k_L(T_L' - T_L) }[/math]. The power output of the engine is [math]\displaystyle{ \dot W = \dot Q_H - \dot Q_L }[/math].

Side note: if one cycle of the engine takes time [math]\displaystyle{ t }[/math], and during this time, it is in contact with the hot side only for a time [math]\displaystyle{ t_H }[/math], then we can reduce to this case by replacing [math]\displaystyle{ k_H }[/math] with [math]\displaystyle{ k_H \frac{t_H}t }[/math]. Similar comments apply to the cold side.

By Carnot theorem, we have [math]\displaystyle{ \eta = \frac{\dot W}{\dot Q_H} \leq 1 - \frac{T_L'}{T_H'} }[/math]. This then gives us a problem of constraint optimization:[math]\displaystyle{ \begin{cases} \max_{T_H', T_L'} \dot W \\ \frac{\dot W}{\dot Q_H} \leq 1 - \frac{T_L'}{T_H'} \end{cases} }[/math]This can be solved by typical methods, such as Lagrange multipliers, giving us[math]\displaystyle{ T_H' = x\sqrt{T_H}; \quad T_L' = x\sqrt{T_L}; \quad x = \frac{k_H\sqrt{T_H} + k_L\sqrt{T_L}}{k_H + k_L} }[/math]at which point the engine is operating at efficiency [math]\displaystyle{ \eta = 1 - \sqrt{\frac{T_L}{T_H}} }[/math].

In particular, if [math]\displaystyle{ k_L \gg k_H }[/math], then we have [math]\displaystyle{ T_H' = \sqrt{T_HT_L}; \quad T_L' = T_L }[/math]This is often the case with practical heat engines in power generation plants, where the work fluid can only spend a small amount of time with the hot bath (nuclear reactor core, coal furnance, etc), but a much larger amount of time with the cold bath (open atmosphere, a large body of water, etc).

Experimental data

For some typical cycles, the above equation (note that absolute temperatures must be used) gives the following results:

Power Plant	[math]\displaystyle{ T_L }[/math] (°C)	[math]\displaystyle{ T_H }[/math] (°C)	[math]\displaystyle{ \eta }[/math] (Carnot)	[math]\displaystyle{ \eta }[/math] (Endoreversible)	[math]\displaystyle{ \eta }[/math] (Observed)
West Thurrock (United Kingdom ) coal-fired power plant	25	565	0.64	0.40	0.36
CANDU (Canada ) nuclear power plant	25	300	0.48	0.28	0.30
Larderello (Italy) geothermal power plant	80	250	0.33	0.178	0.16

As shown, the endoreversible efficiency much more closely models the observed data.

However, such an engine violates Carnot's principle which states that work can be done any time there is a difference in temperature. The fact that the hot and cold reservoirs are not at the same temperature as the working fluid they are in contact with means that work can and is done at the hot and cold reservoirs. The result is tantamount to coupling the high and low temperature parts of the cycle, so that the cycle collapses.

In the Carnot cycle, the working fluid must always remain constant temperatures, as the heat reservoirs they are in contact with and that they are separated by adiabatic transformations which prevent thermal contact. The efficiency was first derived by William Thomson in his study of an unevenly heated body in which the adiabatic partitions between bodies at different temperatures are removed and maximum work is performed. It is well known that the final temperature is the geometric mean temperature [math]\displaystyle{ \sqrt{T_HT_L} }[/math] so that the efficiency is the Carnot efficiency for an engine working between [math]\displaystyle{ T_H }[/math] and [math]\displaystyle{ \sqrt{T_HT_L} }[/math].

See also

An introduction to endoreversible thermodynamics is given in the thesis by Katharina Wagner. It is also introduced by Hoffman et al.

A thorough discussion of the concept, together with many applications in engineering, is given in the book by Hans Ulrich Fuchs.