Physics:Heat engine
| Thermodynamics |
|---|
 |
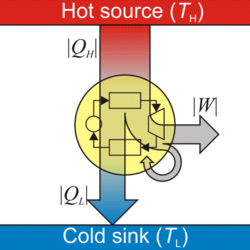
A heat engine is a system that transfers thermal energy to do mechanical or electrical work.[1][2] While originally conceived in the context of mechanical energy, the concept of the heat engine has been applied to various other kinds of energy, particularly electrical, since at least the late 19th century.[3][4] The heat engine does this by bringing a working substance from a higher state temperature to a lower state temperature. A heat source generates thermal energy that brings the working substance to the higher temperature state. The working substance generates work in the working body of the engine while transferring heat to the colder sink until it reaches a lower temperature state. During this process some of the thermal energy is converted into work by exploiting the properties of the working substance. The working substance can be any system with a non-zero heat capacity, but it usually is a gas or liquid. During this process, some heat is normally lost to the surroundings and is not converted to work. Also, some energy is unusable because of friction and drag.
In general, an engine is any machine that converts energy to mechanical work. Heat engines distinguish themselves from other types of engines by the fact that their efficiency is fundamentally limited by Carnot's theorem of thermodynamics.[5] Although this efficiency limitation can be a drawback, an advantage of heat engines is that most forms of energy can be easily converted to heat by processes like exothermic reactions (such as combustion), nuclear fission, absorption of light or energetic particles, friction, dissipation and resistance. Since the heat source that supplies thermal energy to the engine can thus be powered by virtually any kind of energy, heat engines cover a wide range of applications.
Heat engines are often confused with the cycles they attempt to implement. Typically, the term "engine" is used for a physical device and "cycle" for the models.
Overview
In thermodynamics, heat engines are often modeled using a standard engineering model such as the Otto cycle. The theoretical model can be refined and augmented with actual data from an operating engine, using tools such as an indicator diagram. Since very few actual implementations of heat engines exactly match their underlying thermodynamic cycles, one could say that a thermodynamic cycle is an ideal case of a mechanical engine. In any case, fully understanding an engine and its efficiency requires a good understanding of the (possibly simplified or idealised) theoretical model, the practical nuances of an actual mechanical engine and the discrepancies between the two.
In general terms, the larger the difference in temperature between the hot source and the cold sink, the larger is the potential thermal efficiency of the cycle. On Earth, the cold side of any heat engine is limited to being close to the ambient temperature of the environment, or not much lower than 300 kelvin, so most efforts to improve the thermodynamic efficiencies of various heat engines focus on increasing the temperature of the source, within material limits. The maximum theoretical efficiency of a heat engine (which no engine ever attains) is equal to the temperature difference between the hot and cold ends divided by the temperature at the hot end, each expressed in absolute temperature.
The efficiency of various heat engines proposed or used today has a large range:
- 3%[6] (97 percent waste heat using low quality heat) for the ocean thermal energy conversion (OTEC) ocean power proposal
- 25% for most automotive gasoline engines[7]
- 49% for a supercritical coal-fired power station such as the Avedøre Power Station
- 50%+ for low-speed, two-stroke marine diesel engines [8]
- 60% for a combined cycle gas turbine[9]
The efficiency of these processes is roughly proportional to the temperature drop across them. Significant energy may be consumed by auxiliary equipment, such as pumps, which effectively reduces efficiency.
Examples
Although some cycles have a typical combustion location (internal or external), they can often be implemented with the other. For example, John Ericsson[10] developed an external heated engine running on a cycle very much like the earlier Diesel cycle. In addition, externally heated engines can often be implemented in open or closed cycles. In a closed cycle the working fluid is retained within the engine at the completion of the cycle whereas is an open cycle the working fluid is either exchanged with the environment together with the products of combustion in the case of the internal combustion engine or simply vented to the environment in the case of external combustion engines like steam engines and turbines.
Everyday examples
Everyday examples of heat engines include the thermal power station, internal combustion engine, firearms, refrigerators and heat pumps. Power stations are examples of heat engines run in a forward direction in which heat flows from a hot reservoir and flows into a cool reservoir to produce work as the desired product. Refrigerators, air conditioners and heat pumps are examples of heat engines that are run in reverse, i.e. they use work to take heat energy at a low temperature and raise its temperature in a more efficient way than the simple conversion of work into heat (either through friction or electrical resistance). Refrigerators remove heat from within a thermally sealed chamber at low temperature and vent waste heat at a higher temperature to the environment and heat pumps take heat from the low temperature environment and 'vent' it into a thermally sealed chamber (a house) at higher temperature.
In general heat engines exploit the thermal properties associated with the expansion and compression of gases according to the gas laws or the properties associated with phase changes between gas and liquid states.
Earth's heat engine
Earth's atmosphere and hydrosphere—Earth's heat engine—are coupled processes that constantly even out solar heating imbalances through evaporation of surface water, convection, rainfall, winds and ocean circulation, when distributing heat around the globe.[11]
A Hadley cell is an example of a heat engine. It involves the rising of warm and moist air in the earth's equatorial region and the descent of colder air in the subtropics creating a thermally driven direct circulation, with consequent net production of kinetic energy.[12]
Phase-change cycles
In phase change cycles and engines, the working fluids are gases and liquids. The engine converts the working fluid from a gas to a liquid, from liquid to gas, or both, generating work from the fluid expansion or compression.
- Rankine cycle (classical steam engine)
- Regenerative cycle (steam engine more efficient than Rankine cycle)
- Organic Rankine cycle (Coolant changing phase in temperature ranges of ice and hot liquid water)
- Vapor to liquid cycle (drinking bird, injector, Minto wheel)
- Liquid to solid cycle (frost heaving – water changing from ice to liquid and back again can lift rock up to 60 cm.)
- Solid to gas cycle (firearms – solid propellants combust to hot gases.)
Gas-only cycles
In these cycles and engines the working fluid is always a gas (i.e., there is no phase change):
- Carnot cycle (Carnot heat engine)
- Ericsson cycle (Caloric Ship John Ericsson)
- Stirling cycle (Stirling engine,[13] thermoacoustic devices)
- Internal combustion engine (ICE):
- Otto cycle (e.g. gasoline/petrol engine)
- Diesel cycle (e.g. Diesel engine)
- Atkinson cycle (Atkinson engine)
- Brayton cycle or Joule cycle originally Ericsson cycle (gas turbine)
- Lenoir cycle (e.g., pulse jet engine)
- Miller cycle (Miller engine)
Liquid-only cycles
In these cycles and engines the working fluid are always like liquid:
Electron cycles
- Johnson thermoelectric energy converter
- Thermoelectric (Peltier–Seebeck effect)
- Thermogalvanic cell
- Thermionic emission
- Thermotunnel cooling
Magnetic cycles
- Thermo-magnetic motor (Tesla)
Cycles used for refrigeration
A domestic refrigerator is an example of a heat pump: a heat engine in reverse. Work is used to create a heat differential. Many cycles can run in reverse to move heat from the cold side to the hot side, making the cold side cooler and the hot side hotter. Internal combustion engine versions of these cycles are, by their nature, not reversible.
Refrigeration cycles include:
- Air cycle machine
- Gas-absorption refrigerator
- Magnetic refrigeration
- Stirling cryocooler
- Vapor-compression refrigeration
- Vuilleumier cycle
Evaporative heat engines
The Barton evaporation engine is a heat engine based on a cycle producing power and cooled moist air from the evaporation of water into hot dry air.
Mesoscopic heat engines
Mesoscopic heat engines are nanoscale devices that may serve the goal of processing heat fluxes and perform useful work at small scales. Potential applications include e.g. electric cooling devices. In such mesoscopic heat engines, work per cycle of operation fluctuates due to thermal noise. There is exact equality that relates average of exponents of work performed by any heat engine and the heat transfer from the hotter heat bath.[14] This relation transforms the Carnot's inequality into exact equality. This relation is also a Carnot cycle equality
Efficiency
The efficiency of a heat engine relates how much useful work is output for a given amount of heat energy input.
From the laws of thermodynamics, after a completed cycle:[15]
- and therefore
- where
- is the net work extracted from the engine in one cycle. (It is negative, in the IUPAC convention, since work is done by the engine.)
- is the heat energy taken from the high temperature heat source in the surroundings in one cycle. (It is positive since heat energy is added to the engine.)
- is the waste heat given off by the engine to the cold temperature heat sink. (It is negative[15] since heat is lost by the engine to the sink.)
In other words, a heat engine absorbs heat energy from the high temperature heat source, converting part of it to useful work and giving off the rest as waste heat to the cold temperature heat sink.
In general, the efficiency of a given heat transfer process is defined by the ratio of "what is taken out" to "what is put in". (For a refrigerator or heat pump, which can be considered as a heat engine run in reverse, this is the coefficient of performance and it is ≥ 1.) In the case of an engine, one desires to extract work and has to put in heat , for instance from combustion of a fuel, so the engine efficiency is reasonably defined as
The efficiency is less than 100% because of the waste heat unavoidably lost to the cold sink (and corresponding compression work put in) during the required recompression at the cold temperature before the power stroke of the engine can occur again.
The theoretical maximum efficiency of any heat engine depends only on the temperatures it operates between. This efficiency is usually derived using an ideal imaginary heat engine such as the Carnot heat engine, although other engines using different cycles can also attain maximum efficiency. Mathematically, after a full cycle, the overall change of entropy is zero:
Note that is positive because isothermal expansion in the power stroke increases the multiplicity of the working fluid while is negative since recompression decreases the multiplicity. If the engine is ideal and runs reversibly, and , and thus[16][15]
,
which gives and thus the Carnot limit for heat-engine efficiency,
where is the absolute temperature of the hot source and that of the cold sink, usually measured in kelvins.
The reasoning behind this being the maximal efficiency goes as follows. It is first assumed that if a more efficient heat engine than a Carnot engine is possible, then it could be driven in reverse as a heat pump. Mathematical analysis can be used to show that this assumed combination would result in a net decrease in entropy. Since, by the second law of thermodynamics, this is statistically improbable to the point of exclusion, the Carnot efficiency is a theoretical upper bound on the reliable efficiency of any thermodynamic cycle.
Empirically, no heat engine has ever been shown to run at a greater efficiency than a Carnot cycle heat engine.
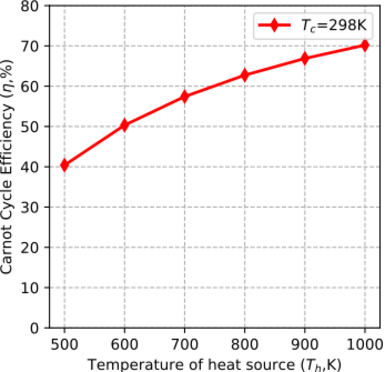
Figure 2 and Figure 3 show variations on Carnot cycle efficiency with temperature. Figure 2 indicates how efficiency changes with an increase in the heat addition temperature for a constant compressor inlet temperature. Figure 3 indicates how the efficiency changes with an increase in the heat rejection temperature for a constant turbine inlet temperature.
 |
 |
Endo-reversible heat-engines
By its nature, any maximally efficient Carnot cycle must operate at an infinitesimal temperature gradient; this is because any transfer of heat between two bodies of differing temperatures is irreversible, therefore the Carnot efficiency expression applies only to the infinitesimal limit. The major problem is that the objective of most heat-engines is to output power, and infinitesimal power is seldom desired.
A different measure of ideal heat-engine efficiency is given by considerations of endoreversible thermodynamics, where the system is broken into reversible subsystems, but with non reversible interactions between them. A classical example is the Curzon–Ahlborn engine,[17] very similar to a Carnot engine, but where the thermal reservoirs at temperature and are allowed to be different from the temperatures of the substance going through the reversible Carnot cycle: and . The heat transfers between the reservoirs and the substance are considered as conductive (and irreversible) in the form . In this case, a tradeoff has to be made between power output and efficiency. If the engine is operated very slowly, the heat flux is low, and the classical Carnot result is found
- ,
but at the price of a vanishing power output. If instead one chooses to operate the engine at its maximum output power, the efficiency becomes
This model does a better job of predicting how well real-world heat-engines can do (Callen 1985, see also endoreversible thermodynamics):
| Power station | (°C) | (°C) | (Carnot) | (Endoreversible) | (Observed) |
|---|---|---|---|---|---|
| West Thurrock (UK) coal-fired power station | 25 | 565 | 0.64 | 0.40 | 0.36 |
| CANDU (Canada) nuclear power station | 25 | 300 | 0.48 | 0.28 | 0.30 |
| Larderello (Italy) geothermal power station | 80 | 250 | 0.33 | 0.178 | 0.16 |
As shown, the Curzon–Ahlborn efficiency much more closely models that observed.
History
Heat engines have been known since antiquity but were only made into useful devices at the time of the industrial revolution in the 18th century. They continue to be developed today.
Enhancements
Engineers have studied the various heat-engine cycles to improve the amount of usable work they could extract from a given power source. The Carnot cycle limit cannot be reached with any gas-based cycle, but engineers have found at least two ways to bypass that limit and one way to get better efficiency without bending any rules:
- Increase the temperature difference in the heat engine. The simplest way to do this is to increase the hot side temperature, which is the approach used in modern combined-cycle gas turbines. Unfortunately, physical limits (such as the melting point of the materials used to build the engine) and environmental concerns regarding NOx production (if the heat source is combustion with ambient air) restrict the maximum temperature on workable heat-engines. Modern gas turbines run at temperatures as high as possible within the range of temperatures necessary to maintain acceptable NOx output . Another way of increasing efficiency is to lower the output temperature. One new method of doing so is to use mixed chemical working fluids, then exploit the changing behavior of the mixtures. One of the most famous is the so-called Kalina cycle, which uses a 70/30 mix of ammonia and water as its working fluid. This mixture allows the cycle to generate useful power at considerably lower temperatures than most other processes.
- Exploit the physical properties of the working fluid. The most common such exploitation is the use of water above the critical point (supercritical water). The behavior of fluids above their critical point changes radically, and with materials such as water and carbon dioxide it is possible to exploit those changes in behavior to extract greater thermodynamic efficiency from the heat engine, even if it is using a fairly conventional Brayton or Rankine cycle. A newer and very promising material for such applications is supercritical CO2. SO2 and xenon have also been considered for such applications. Downsides include issues of corrosion and erosion, the different chemical behavior above and below the critical point, the needed high pressures and – in the case of sulfur dioxide and to a lesser extent carbon dioxide – toxicity. Among the mentioned compounds xenon is least suitable for use in a nuclear reactor due to the high neutron absorption cross section of almost all isotopes of xenon, whereas carbon dioxide and water can also double as a neutron moderator for a thermal spectrum reactor.
- Exploit the chemical properties of the working fluid. A fairly new and novel exploit is to use exotic working fluids with advantageous chemical properties. One such is nitrogen dioxide (NO2), a toxic component of smog, which has a natural dimer as di-nitrogen tetraoxide (N2O4). At low temperature, the N2O4 is compressed and then heated. The increasing temperature causes each N2O4 to break apart into two NO2 molecules. This lowers the molecular weight of the working fluid, which drastically increases the efficiency of the cycle. Once the NO2 has expanded through the turbine, it is cooled by the heat sink, which makes it recombine into N2O4. This is then fed back by the compressor for another cycle. Such species as aluminium bromide (Al2Br6), NOCl, and Ga2I6 have all been investigated for such uses. To date, their drawbacks have not warranted their use, despite the efficiency gains that can be realized.[18]
Heat engine processes
Template:Table of thermodynamic cycles
Each process is one of the following:
- isothermal (at constant temperature, maintained with heat added or removed from a heat source or sink)
- isobaric (at constant pressure)
- isometric/isochoric (at constant volume), also referred to as iso-volumetric
- adiabatic (no heat is added or removed from the system during adiabatic process)
- isentropic (reversible adiabatic process, no heat is added or removed during isentropic process)
See also
- Carnot heat engine
- Cogeneration
- Einstein refrigerator
- Heat pump
- Reciprocating engine for a general description of the mechanics of piston engines
- Stirling engine
- Thermosynthesis
- Timeline of heat engine technology
References
- ↑ Fundamentals of Classical Thermodynamics, 3rd ed. p. 159, (1985) by G. J. Van Wylen and R. E. Sonntag: "A heat engine may be defined as a device that operates in thermodynamic cycle and does a certain amount of net positive work as a result of heat transfer from a high-temperature body to a low-temperature body. Often the term heat engine is used in a broader sense to include all devices that produce work, either through heat transfer or combustion, even though the device does not operate in a thermodynamic cycle. The internal-combustion engine and the gas turbine are examples of such devices, and calling these heat engines is an acceptable use of the term."
- ↑ Mechanical efficiency of heat engines, p. 1 (2007) by James R. Senf: "Heat engines are made to provide mechanical energy from thermal energy."
- ↑ Kenelly, A.E. (Dec 1898). "Discussion of 'Thermo-electric and galvanic actions compared'". Journal of the Franklin Society CXLVI: 442. https://books.google.com/books?id=nXooAQAAIAAJ&pg=PA442.
- ↑ Laurie, Arthur Pillans (17 Jan 1914). "Faraday society". The Electrical Review 72 (1834): 90. https://books.google.com/books?id=fko1AQAAMAAJ&pg=PA90. Retrieved 11 February 2023.
- ↑ Thermal physics: entropy and free energies, by Joon Chang Lee (2002), Appendix A, p. 183: "A heat engine absorbs energy from a heat source and then converts it into work for us.... When the engine absorbs heat energy, the absorbed heat energy comes with entropy." (heat energy ), "When the engine performs work, on the other hand, no entropy leaves the engine. This is problematic. We would like the engine to repeat the process again and again to provide us with a steady work source. ... to do so, the working substance inside the engine must return to its initial thermodynamic condition after a cycle, which requires to remove the remaining entropy. The engine can do this only in one way. It must let part of the absorbed heat energy leave without converting it into work. Therefore the engine cannot convert all of the input energy into work!"
- ↑ Eman, Mahmod Mohamed (June 2013). "Experimental Investigations on a Standing-Wave Thermoacoustic Engine". ResearchGate (Giza, Egypt: Cairo University). https://www.researchgate.net/publication/237251713. Retrieved 21 January 2018.
- ↑ Where the Energy Goes: Gasoline Vehicles, US Dept of Energy
- ↑ Takaishi, Tatsuo; Numata, Akira; Nakano, Ryouji; Sakaguchi, Katsuhiko (2008). "Approach to High Efficiency Diesel and Gas Engines". Mitsubishi Heavy Industries, Ltd.. https://www.mhi.co.jp/technology/review/pdf/e451/e451021.pdf.
- ↑ Langston, Lee S.. "Efficiency by the Numbers". ASME. https://memagazineblog.org/2012/07/01/efficiency-by-the-numbers/.
- ↑ "Ericsson's 1833 caloric engine". hotairengines.org. http://hotairengines.org/closed-cycle-engine/ericsson-1833.
- ↑ Lindsey, Rebecca (2009). "Climate and Earth's Energy Budget". NASA Earth Observatory. http://earthobservatory.nasa.gov/Features/EnergyBalance/.
- ↑ Junling Huang and Michael B. McElroy (2014). "Contributions of the Hadley and Ferrel Circulations to the Energetics of the Atmosphere over the Past 32 Years". Journal of Climate 27 (7): 2656–2666. doi:10.1175/jcli-d-13-00538.1. Bibcode: 2014JCli...27.2656H.
- ↑ "Stirling's Dundee engine of 1841". hotairengines.org. http://hotairengines.org/closed-cycle-engine/stirling-1827/stirling-dundee-engine.
- ↑ N. A. Sinitsyn (2011). "Fluctuation Relation for Heat Engines". J. Phys. A: Math. Theor. 44 (40). doi:10.1088/1751-8113/44/40/405001. Bibcode: 2011JPhA...44N5001S.
- ↑ 15.0 15.1 15.2 Planck, M. (1945). Treatise on Thermodynamics. Dover Publications. p. § 90 & § 137. "eqs.(39), (40), & (65)".
- ↑ Fermi, E. (1956). Thermodynamics. Dover Publications (still in print). p. 48. "eq.(64)".
- ↑ 17.0 17.1 F. L. Curzon, B. Ahlborn (1975). "Efficiency of a Carnot Engine at Maximum Power Output". Am. J. Phys., Vol. 43, pp. 24.
- ↑ "Nuclear Reactors Concepts and Thermodynamic Cycles". https://netfiles.uiuc.edu/mragheb/www/NPRE%20402%20ME%20405%20Nuclear%20Power%20Engineering/Nuclear%20Reactors%20Concepts%20and%20Thermodynamic%20Cycles.pdf.
- Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 0-7167-1088-9.
- Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics (2nd ed.). John Wiley & Sons, Inc.. ISBN 0-471-86256-8.
- Robinson, Clark (1943). The Thermodynamics of Firearms. MaGraw-Hill Book Company Inc..
 |
