Physics:Work (thermodynamics)

Short description: Type of energy transfer

Thermodynamic work is one of the principal processes by which a thermodynamic system can interact with its surroundings and exchange energy. This exchange results in externally measurable macroscopic forces on the system's surroundings, which can cause mechanical work, to lift a weight, for example, or cause changes in electromagnetic, or gravitational variables. The surroundings also can perform work on a thermodynamic system, which is measured by an opposite sign convention.

For thermodynamic work, appropriately chosen externally measured quantities are exactly matched by values of or contributions to changes in macroscopic internal state variables of the system, which always occur in conjugate pairs, for example pressure and volume or magnetic flux density and magnetization.

In the International System of Units (SI), work is measured in joules (symbol J). The rate at which work is performed is power, measured in joules per second, and denoted with the unit watt (W).

History

1824

Work, i.e. "weight lifted through a height", was originally defined in 1824 by Sadi Carnot in his famous paper Reflections on the Motive Power of Fire, where he used the term motive power for work. Specifically, according to Carnot:

We use here motive power to express the useful effect that a motor is capable of producing. This effect can always be likened to the elevation of a weight to a certain height. It has, as we know, as a measure, the product of the weight multiplied by the height to which it is raised.

1845

Joule's apparatus for measuring the mechanical equivalent of heat

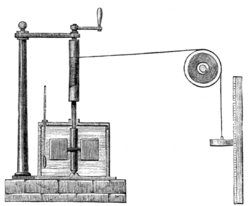
In 1845, the English physicist James Joule wrote a paper On the mechanical equivalent of heat for the British Association meeting in Cambridge. In this paper, he reported his best-known experiment, in which the mechanical power released through the action of a "weight falling through a height" was used to turn a paddle-wheel in an insulated barrel of water.

In this experiment, the motion of the paddle wheel, through agitation and friction, heated the body of water, so as to increase its temperature. Both the temperature change [math]\displaystyle{ \Delta T }[/math] of the water and the height of the fall [math]\displaystyle{ \Delta h }[/math] of the weight [math]\displaystyle{ mg }[/math] were recorded. Using these values, Joule was able to determine the mechanical equivalent of heat. Joule estimated a mechanical equivalent of heat to be 819 ft•lbf/Btu (4.41 J/cal). The modern day definitions of heat, work, temperature, and energy all have connection to this experiment. In this arrangement of apparatus, it never happens that the process runs in reverse, with the water driving the paddles so as to raise the weight, not even slightly. Mechanical work was done by the apparatus of falling weight, pulley, and paddles, which lay in the surroundings of the water. Their motion scarcely affected the volume of the water. A quantity of mechanical work, measured as force × distance in the surroundings, that does not change the volume of the water, is said to be isochoric. Such work reaches the system only as friction, through microscopic modes, and is irreversible. It does not count as thermodynamic work. The energy supplied by the fall of the weight passed into the water as heat.

Overview

Conservation of energy

A pre-supposed guiding principle of thermodynamics is the conservation of energy. The total energy of a system is the sum of its internal energy, of its potential energy as a whole system in an external force field, such as gravity, and of its kinetic energy as a whole system in motion. Thermodynamics has special concern with transfers of energy, from a body of matter, such as, for example a cylinder of steam, to the surroundings of the body, by mechanisms through which the body exerts macroscopic forces on its surroundings so as to lift a weight there; such mechanisms are the ones that are said to mediate thermodynamic work.

Besides transfer of energy as work, thermodynamics admits transfer of energy as heat. For a process in a closed (no transfer of matter) thermodynamic system, the first law of thermodynamics relates changes in the internal energy (or other cardinal energy function, depending on the conditions of the transfer) of the system to those two modes of energy transfer, as work, and as heat. Adiabatic work is done without matter transfer and without heat transfer. In principle, in thermodynamics, for a process in a closed system, the quantity of heat transferred is defined by the amount of adiabatic work that would be needed to effect the change in the system that is occasioned by the heat transfer. In experimental practice, heat transfer is often estimated calorimetrically, through change of temperature of a known quantity of calorimetric material substance.

Energy can also be transferred to or from a system through transfer of matter. The possibility of such transfer defines the system as an open system, as opposed to a closed system. By definition, such transfer is neither as work nor as heat.

Changes in the potential energy of a body as a whole with respect to forces in its surroundings, and in the kinetic energy of the body moving as a whole with respect to its surroundings, are by definition excluded from the body's cardinal energy (examples are internal energy and enthalpy).

Nearly reversible transfer of energy by work in the surroundings

In the surroundings of a thermodynamic system, external to it, all the various mechanical and non-mechanical macroscopic forms of work can be converted into each other with no limitation in principle due to the laws of thermodynamics, so that the energy conversion efficiency can approach 100% in some cases; such conversion is required to be frictionless, and consequently adiabatic. In particular, in principle, all macroscopic forms of work can be converted into the mechanical work of lifting a weight, which was the original form of thermodynamic work considered by Carnot and Joule (see History section above). Some authors have considered this equivalence to the lifting of a weight as a defining characteristic of work. For example, with the apparatus of Joule's experiment in which, through pulleys, a weight descending in the surroundings drives the stirring of a thermodynamic system, the descent of the weight can be diverted by a re-arrangement of pulleys, so that it lifts another weight in the surroundings, instead of stirring the thermodynamic system.

Such conversion may be idealized as nearly frictionless, though it occurs relatively quickly. It usually comes about through devices that are not simple thermodynamic systems (a simple thermodynamic system is a homogeneous body of material substances). For example, the descent of the weight in Joule's stirring experiment reduces the weight's total energy. It is described as loss of gravitational potential energy by the weight, due to change of its macroscopic position in the gravity field, in contrast to, for example, loss of the weight's internal energy due to changes in its entropy, volume, and chemical composition. Though it occurs relatively rapidly, because the energy remains nearly fully available as work in one way or another, such diversion of work in the surroundings may be idealized as nearly reversible, or nearly perfectly efficient.

In contrast, the conversion of heat into work in a heat engine can never exceed the Carnot efficiency, as a consequence of the second law of thermodynamics. Such energy conversion, through work done relatively rapidly, in a practical heat engine, by a thermodynamic system on its surroundings, cannot be idealized, not even nearly, as reversible.

Thermodynamic work done by a thermodynamic system on its surroundings is defined so as to comply with this principle. Historically, thermodynamics was about how a thermodynamic system could do work on its surroundings.

Work done by and on a simple thermodynamic system

Work done on, and work done by, a thermodynamic system need to be distinguished, through consideration of their precise mechanisms. Work done on a thermodynamic system, by devices or systems in the surroundings, is performed by actions such as compression, and includes shaft work, stirring, and rubbing. Such work done by compression is thermodynamic work as here defined. But shaft work, stirring, and rubbing are not thermodynamic work as here defined, in that they do not change the volume of the system against its resisting pressure. Work without change of volume is known as isochoric work, for example when an agency, in the surroundings of the system, drives a frictional action on the surface or in the interior of the system.

In a process of transfer of energy from or to a thermodynamic system, the change of internal energy of the system is defined in theory by the amount of adiabatic work that would have been necessary to reach the final from the initial state, such adiabatic work being measurable only through the externally measurable mechanical or deformation variables of the system, that provide full information about the forces exerted by the surroundings on the system during the process. In the case of some of Joule's measurements, the process was so arranged that some heating that occurred outside the system (in the substance of the paddles) by the frictional process also led to heat transfer from the paddles into the system during the process, so that the quantity of work done by the surrounds on the system could be calculated as shaft work, an external mechanical variable.

The amount of energy transferred as work is measured through quantities defined externally to the system of interest, and thus belonging to its surroundings. In an important sign convention, preferred in chemistry, work that adds to the internal energy of the system is counted as positive. On the other hand, for historical reasons, an oft-encountered sign convention, preferred in physics, is to consider work done by the system on its surroundings as positive.

Processes not described by macroscopic work

Transfer of thermal energy through direct contact between a closed system and its surroundings, is by the microscopic thermal motions of particles and their associated inter-molecular potential energies. The microscopic description of such processes are the province of statistical mechanics, not of macroscopic thermodynamics. Another kind of energy transfer is by radiation, performing work on the system. Radiative transfer of energy is irreversible in the sense that it occurs only from a hotter to a colder system. There are several forms of dissipative transduction of energy that can occur internally within a system at a microscopic level, such as friction including bulk and shear viscosity chemical reaction, unconstrained expansion as in Joule expansion and in diffusion, and phase change.

Open systems

For an open system, the first law of thermodynamics admits three forms of energy transfer, as work, as heat, and as energy associated with matter that is transferred. The latter cannot be split uniquely into heat and work components.

One-way convection of internal energy is a form a transport of energy but is not, as sometimes mistakenly supposed (a relic of the caloric theory of heat), transfer of energy as heat, because one-way convection is transfer of matter; nor is it transfer of energy as work. Nevertheless, if the wall between the system and its surroundings is thick and contains fluid, in the presence of a gravitational field, convective circulation within the wall can be considered as indirectly mediating transfer of energy as heat between the system and its surroundings, though the source and destination of the transferred energy are not in direct contact.

Fictively imagined reversible thermodynamic "processes"

For purposes of theoretical calculations about a thermodynamic system, one can imagine fictive idealized thermodynamic "processes" that occur so slowly that they do not incur friction within or on the surface of system; they can then be regarded as virtually reversible. These fictive processes proceed along paths on geometrical surfaces that are described exactly by a characteristic equation of the thermodynamic system. Those geometrical surfaces are the loci of possible states of thermodynamic equilibrium for the system. Really possible thermodynamic processes, occurring at practical rates, even when they occur only by work assessed in the surroundings as adiabatic, without heat transfer, always incur friction within the system, and so are always irreversible. The paths of such really possible processes always depart from those geometrical characteristic surfaces. Even when they occur only by work assessed in the surroundings as adiabatic, without heat transfer, such departures always entail entropy production.

Joule heating and rubbing

The definition of thermodynamic work is in terms of the changes of the system's extensive deformation (and chemical constitutive and certain other) state variables, such as volume, molar chemical constitution, or electric polarisation. Examples of state variables that are not extensive deformation or other such variables are temperature T and entropy S, as for example in the expression U = U(S, V, {N_j}). Changes of such variables are not actually physically measureable by use of a single simple adiabatic thermodynamic process; they are processes that occur neither by thermodynamic work nor by transfer of matter, and therefore are said occur by heat transfer. The quantity of thermodynamic work is defined as work done by the system on its surroundings. According to the second law of thermodynamics, such work is irreversible. To get an actual and precise physical measurement of a quantity of thermodynamic work, it is necessary to take account of the irreversibility by restoring the system to its initial condition by running a cycle, for example a Carnot cycle, that includes the target work as a step. The work done by the system on its surroundings is calculated from the quantities that constitute the whole cycle. A different cycle would be needed to actually measure the work done by the surroundings on the system. This is a reminder that rubbing the surface of a system appears to the rubbing agent in the surroundings as mechanical, though not thermodynamic, work done on the system, not as heat, but appears to the system as heat transferred to the system, not as thermodynamic work. The production of heat by rubbing is irreversible; historically, it was a piece of evidence for the rejection of the caloric theory of heat as a conserved substance. The irreversible process known as Joule heating also occurs through a change of a non-deformation extensive state variable.

Accordingly, in the opinion of Lavenda, work is not as primitive concept as is heat, which can be measured by calorimetry. This opinion does not negate the now customary thermodynamic definition of heat in terms of adiabatic work.

Known as a thermodynamic operation, the initiating factor of a thermodynamic process is, in many cases, a change in the permeability of a wall between the system and the surroundings. Rubbing is not a change in wall permeability. Kelvin's statement of the second law of thermodynamics uses the notion of an "inanimate material agency"; this notion is sometimes regarded as puzzling. The triggering of a process of rubbing can occur only in the surroundings, not in a thermodynamic system in its own state of internal thermodynamic equilibrium. Such triggering may be described as a thermodynamic operation.

Formal definition

In thermodynamics, the quantity of work done by a closed system on its surroundings is defined by factors strictly confined to the interface of the surroundings with the system and to the surroundings of the system, for example, an extended gravitational field in which the system sits, that is to say, to things external to the system.

A main concern of thermodynamics is the properties of materials. Thermodynamic work is defined for the purposes of thermodynamic calculations about bodies of material, known as thermodynamic systems. Consequently, thermodynamic work is defined in terms of quantities that describe the states of materials, which appear as the usual thermodynamic state variables, such as volume, pressure, temperature, chemical composition, and electric polarization. For example, to measure the pressure inside a system from outside it, the observer needs the system to have a wall that can move by a measurable amount in response to pressure differences between the interior of the system and the surroundings. In this sense, part of the definition of a thermodynamic system is the nature of the walls that confine it.

Several kinds of thermodynamic work are especially important. One simple example is pressure–volume work. The pressure of concern is that exerted by the surroundings on the surface of the system, and the volume of interest is the negative of the increment of volume gained by the system from the surroundings. It is usually arranged that the pressure exerted by the surroundings on the surface of the system is well defined and equal to the pressure exerted by the system on the surroundings. This arrangement for transfer of energy as work can be varied in a particular way that depends on the strictly mechanical nature of pressure–volume work. The variation consists in letting the coupling between the system and surroundings be through a rigid rod that links pistons of different areas for the system and surroundings. Then for a given amount of work transferred, the exchange of volumes involves different pressures, inversely with the piston areas, for mechanical equilibrium. This cannot be done for the transfer of energy as heat because of its non-mechanical nature.

Another important kind of work is isochoric work, i.e., work that involves no eventual overall change of volume of the system between the initial and the final states of the process. Examples are friction on the surface of the system as in Rumford's experiment; shaft work such as in Joule's experiments; stirring of the system by a magnetic paddle inside it, driven by a moving magnetic field from the surroundings; and vibrational action on the system that leaves its eventual volume unchanged, but involves friction within the system. Isochoric mechanical work for a body in its own state of internal thermodynamic equilibrium is done only by the surroundings on the body, not by the body on the surroundings, so that the sign of isochoric mechanical work with the physics sign convention is always negative.

When work, for example pressure–volume work, is done on its surroundings by a closed system that cannot pass heat in or out because it is confined by an adiabatic wall, the work is said to be adiabatic for the system as well as for the surroundings. When mechanical work is done on such an adiabatically enclosed system by the surroundings, it can happen that friction in the surroundings is negligible, for example in the Joule experiment with the falling weight driving paddles that stir the system. Such work is adiabatic for the surroundings, even though it is associated with friction within the system. Such work may or may not be isochoric for the system, depending on the system and its confining walls. If it happens to be isochoric for the system (and does not eventually change other system state variables such as magnetization), it appears as a heat transfer to the system, and does not appear to be adiabatic for the system.

Sign convention

In the early history of thermodynamics, a positive amount of work done by the system on the surroundings leads to energy being lost from the system. This historical sign convention has been used in many physics textbooks and is used in the present article.

According to the first law of thermodynamics for a closed system, any net change in the internal energy U must be fully accounted for, in terms of heat Q entering the system and work W done by the system:

[math]\displaystyle{ \Delta U = Q - W.\; }[/math]

An alternate sign convention is to consider the work performed on the system by its surroundings as positive. This leads to a change in sign of the work, so that [math]\displaystyle{ \Delta U = Q + W }[/math]. This convention has historically been used in chemistry, and has been adopted by most physics textbooks.

This equation reflects the fact that the heat transferred and the work done are not properties of the state of the system. Given only the initial state and the final state of the system, one can only say what the total change in internal energy was, not how much of the energy went out as heat, and how much as work. This can be summarized by saying that heat and work are not state functions of the system. This is in contrast to classical mechanics, where net work exerted by a particle is a state function.

Pressure–volume work

Pressure–volume work (or PV or P-V work) occurs when the volume V of a system changes. PV work is often measured in units of litre-atmospheres where 1L·atm = 101.325J. However, the litre-atmosphere is not a recognized unit in the SI system of units, which measures P in pascals (Pa), V in m³, and PV in joules (J), where 1 J = 1 Pa·m³. PV work is an important topic in chemical thermodynamics.

For a process in a closed system, occurring slowly enough for accurate definition of the pressure on the inside of the system's wall that moves and transmits force to the surroundings, described as quasi-static, work is represented by the following equation between differentials:

[math]\displaystyle{ \delta W = P \, dV }[/math] where

• [math]\displaystyle{ \delta W }[/math] (inexact differential) denotes an infinitesimal increment of work done by the system, transferring energy to the surroundings;
• [math]\displaystyle{ P }[/math] denotes the pressure inside the system, that it exerts on the moving wall that transmits force to the surroundings. In the alternative sign convention the right hand side has a negative sign.
• [math]\displaystyle{ dV }[/math] (exact differential) denotes an infinitesimal increment of the volume of the system.

Moreover, [math]\displaystyle{ W=\int_{V_i}^{V_f} P\,dV. }[/math] where [math]\displaystyle{ W }[/math] denotes the work done by the system during the whole of the reversible process.

The first law of thermodynamics can then be expressed as [math]\displaystyle{ dU = \delta Q - P dV \, . }[/math]

(In the alternative sign convention where W = work done on the system, [math]\displaystyle{ \delta W = - P \, dV }[/math]. However, [math]\displaystyle{ dU = \delta Q - P \, dV }[/math] is unchanged.)

Path dependence

PV work is path-dependent and is, therefore, a thermodynamic process function. In general, the term [math]\displaystyle{ P\,dV }[/math] is not an exact differential. The statement that a process is quasi-static gives important information about the process but does not determine the P–V path uniquely, because the path can include several slow goings backwards and forward in volume, slowly enough to exclude friction within the system occasioned by departure from the quasi-static requirement. An adiabatic wall is one that does not permit passage of energy by conduction or radiation.

The first law of thermodynamics states that [math]\displaystyle{ \Delta U = Q - W }[/math].

For a quasi-static adiabatic process, [math]\displaystyle{ \delta Q = 0 }[/math] so that [math]\displaystyle{ Q = \int \delta Q = 0. }[/math] Also [math]\displaystyle{ \delta W = PdV }[/math] so that [math]\displaystyle{ W = \int \delta W = \int P \, dV . }[/math] It follows that [math]\displaystyle{ dU = - \delta W }[/math] so that [math]\displaystyle{ \Delta U = - \int P \, dV. }[/math] Internal energy is a state function so its change depends only on the initial and final states of a process. For a quasi-static adiabatic process, the change in internal energy is equal to minus the integral amount of work done by the system, so the work also depends only on the initial and final states of the process and is one and the same for every intermediate path. As a result, the work done by the system also depends on the initial and final states.

If the process path is other than quasi-static and adiabatic, there are indefinitely many different paths, with significantly different work amounts, between the initial and final states. (Again the internal energy change depends only on the initial and final states as it is a state function).

In the current mathematical notation, the differential [math]\displaystyle{ \delta W }[/math] is an inexact differential.

In another notation, δW is written đW (with a horizontal line through the d). This notation indicates that đW is not an exact one-form. The line-through is merely a flag to warn us there is actually no function (0-form) W which is the potential of đW. If there were, indeed, this function W, we should be able to just use Stokes Theorem to evaluate this putative function, the potential of đW, at the boundary of the path, that is, the initial and final points, and therefore the work would be a state function. This impossibility is consistent with the fact that it does not make sense to refer to the work on a point in the PV diagram; work presupposes a path.

Other mechanical types of work

There are several ways of doing mechanical work, each in some way related to a force acting through a distance. In basic mechanics, the work done by a constant force F on a body displaced a distance s in the direction of the force is given by

[math]\displaystyle{ W = F s }[/math]

If the force is not constant, the work done is obtained by integrating the differential amount of work,

[math]\displaystyle{ W=\int_1^2 F\,ds. }[/math]

Rotational work

Energy transmission with a rotating shaft is very common in engineering practice. Often the torque T applied to the shaft is constant which means that the force F applied is constant. For a specified constant torque, the work done during n revolutions is determined as follows: A force F acting through a moment arm r generates a torque T

[math]\displaystyle{ T = F r \implies F = \frac{T}{r} }[/math]

This force acts through a distance s, which is related to the radius r by

[math]\displaystyle{ s = 2 r\pi n }[/math]

The shaft work is then determined from:

[math]\displaystyle{ W_s = F s=2 \pi n T }[/math]

The power transmitted through the shaft is the shaft work done per unit time, which is expressed as

[math]\displaystyle{ \dot{W}_s=2 \pi T \dot{n} }[/math]

Spring work

When a force is applied on a spring, and the length of the spring changes by a differential amount dx, the work done is

[math]\displaystyle{ \partial w_s=F dx }[/math]

For linear elastic springs, the displacement x is proportional to the force applied

[math]\displaystyle{ F = Kx, }[/math]

where K is the spring constant and has the unit of N/m. The displacement x is measured from the undisturbed position of the spring (that is, X = 0 when F = 0). Substituting the two equations

[math]\displaystyle{ W_s=\frac{1}{2} k \left(x_1^2 - x_2^2\right) }[/math],

where x₁ and x₂ are the initial and the final displacement of the spring respectively, measured from the undisturbed position of the spring.

Work done on elastic solid bars

Solids are often modeled as linear springs because under the action of a force they contract or elongate, and when the force is lifted, they return to their original lengths, like a spring. This is true as long as the force is in the elastic range, that is, not large enough to cause permanent or plastic deformation. Therefore, the equations given for a linear spring can also be used for elastic solid bars. Alternately, we can determine the work associated with the expansion or contraction of an elastic solid bar by replacing the pressure P by its counterpart in solids, normal stress σ = F/A in the work expansion

[math]\displaystyle{ W=\int_1^2 F\,dx. }[/math]

[math]\displaystyle{ W=\int_1^2 A \sigma\,dx. }[/math]

where A is the cross sectional area of the bar.

Work associated with the stretching of liquid film

Consider a liquid film such as a soap film suspended on a wire frame. Some force is required to stretch this film by the movable portion of the wire frame. This force is used to overcome the microscopic forces between molecules at the liquid-air interface. These microscopic forces are perpendicular to any line in the surface and the force generated by these forces per unit length is called the surface tension σ whose unit is N/m. Therefore, the work associated with the stretching of a film is called surface tension work, and is determined from

[math]\displaystyle{ W_s=\int_1^2 \sigma_s\,dA. }[/math]

where dA=2b dx is the change in the surface area of the film. The factor 2 is due to the fact that the film has two surfaces in contact with air. The force acting on the moveable wire as a result of surface tension effects is F = 2b σ, where σ is the surface tension force per unit length.

Free energy and energy

The amount of useful work that may be extracted from a thermodynamic system is determined by the second law of thermodynamics. Under many practical situations this can be represented by the thermodynamic availability, or Exergy, function. Two important cases are: in thermodynamic systems where the temperature and volume are held constant, the measure of useful work attainable is the Helmholtz free energy function; and in systems where the temperature and pressure are held constant, the measure of useful work attainable is the Gibbs free energy.

Non-mechanical forms of work

Non-mechanical work in thermodynamics is work caused by external force fields that a system is exposed to. The action of such forces can be initiated by events in the surroundings of the system, or by thermodynamic operations on the shielding walls of the system.

The non-mechanical work of force fields can have either positive or negative sign, work being done by the system on the surroundings, or vice versa. Work done by force fields can be done indefinitely slowly, so as to approach the fictive reversible quasi-static ideal, in which entropy is not created in the system by the process.

In thermodynamics, non-mechanical work is to be contrasted with mechanical work that is done by forces in immediate contact between the system and its surroundings. If the putative 'work' of a process cannot be defined as either long-range work or else as contact work, then sometimes it cannot be described by the thermodynamic formalism as work at all. Nevertheless, the thermodynamic formalism allows that energy can be transferred between an open system and its surroundings by processes for which work is not defined. An example is when the wall between the system and its surrounds is not considered as idealized and vanishingly thin, so that processes can occur within the wall, such as friction affecting the transfer of matter across the wall; in this case, the forces of transfer are neither strictly long-range nor strictly due to contact between the system and its surroundings; the transfer of energy can then be considered as convection, and assessed in sum just as transfer of internal energy. This is conceptually different from transfer of energy as heat through a thick fluid-filled wall in the presence of a gravitational field, between a closed system and its surroundings; in this case there may convective circulation within the wall but the process may still be considered as transfer of energy as heat between the system and its surroundings; if the whole wall is moved by the application of force from the surroundings, without change of volume of the wall, so as to change the volume of the system, then it is also at the same time transferring energy as work. A chemical reaction within a system can lead to electrical long-range forces and to electric current flow, which transfer energy as work between system and surroundings, though the system's chemical reactions themselves (except for the special limiting case in which in they are driven through devices in the surroundings so as to occur along a line of thermodynamic equilibrium) are always irreversible and do not directly interact with the surroundings of the system.

Non-mechanical work contrasts with pressure–volume work. Pressure–volume work is one of the two mainly considered kinds of mechanical contact work. A force acts on the interfacing wall between system and surroundings. The force is due to the pressure exerted on the interfacing wall by the material inside the system; that pressure is an internal state variable of the system, but is properly measured by external devices at the wall. The work is due to change of system volume by expansion or contraction of the system. If the system expands, in the present article it is said to do positive work on the surroundings. If the system contracts, in the present article it is said to do negative work on the surroundings. Pressure–volume work is a kind of contact work, because it occurs through direct material contact with the surrounding wall or matter at the boundary of the system. It is accurately described by changes in state variables of the system, such as the time courses of changes in the pressure and volume of the system. The volume of the system is classified as a "deformation variable", and is properly measured externally to the system, in the surroundings. Pressure–volume work can have either positive or negative sign. Pressure–volume work, performed slowly enough, can be made to approach the fictive reversible quasi-static ideal.

Non-mechanical work also contrasts with shaft work. Shaft work is the other of the two mainly considered kinds of mechanical contact work. It transfers energy by rotation, but it does not eventually change the shape or volume of the system. Because it does not change the volume of the system it is not measured as pressure–volume work, and it is called isochoric work. Considered solely in terms of the eventual difference between initial and final shapes and volumes of the system, shaft work does not make a change. During the process of shaft work, for example the rotation of a paddle, the shape of the system changes cyclically, but this does not make an eventual change in the shape or volume of the system. Shaft work is a kind of contact work, because it occurs through direct material contact with the surrounding matter at the boundary of the system. A system that is initially in a state of thermodynamic equilibrium cannot initiate any change in its internal energy. In particular, it cannot initiate shaft work. This explains the curious use of the phrase "inanimate material agency" by Kelvin in one of his statements of the second law of thermodynamics. Thermodynamic operations or changes in the surroundings are considered to be able to create elaborate changes such as indefinitely prolonged, varied, or ceased rotation of a driving shaft, while a system that starts in a state of thermodynamic equilibrium is inanimate and cannot spontaneously do that. Thus the sign of shaft work is always negative, work being done on the system by the surroundings. Shaft work can hardly be done indefinitely slowly; consequently it always produces entropy within the system, because it relies on friction or viscosity within the system for its transfer. The foregoing comments about shaft work apply only when one ignores that the system can store angular momentum and its related energy.

Examples of non-mechanical work modes include

• Electric field work – where the force is defined by the surroundings' voltage (the electrical potential) and the generalized displacement is change of spatial distribution of electrical charge
• Electrical polarization work – where the force is defined by the surroundings' electric field strength and the generalized displacement is change of the polarization of the medium (the sum of the electric dipole moments of the molecules)
• Magnetic work – where the force is defined by the surroundings' magnetic field strength and the generalized displacement is change of total magnetic dipole moment

Gravitational work

Gravitational work is defined by the force on a body measured in a gravitational field. It may cause a generalized displacement in the form of change of the spatial distribution of the matter within the system. The system gains internal energy (or other relevant cardinal quantity of energy, such as enthalpy) through internal friction. As seen by the surroundings, such frictional work appears as mechanical work done on the system, but as seen by the system, it appears as transfer of energy as heat. When the system is in its own state of internal thermodynamic equilibrium, its temperature is uniform throughout. If the volume and other extensive state variables, apart from entropy, are held constant over the process, then the transferred heat must appear as increased temperature and entropy; in a uniform gravitational field, the pressure of the system will be greater at the bottom than at the top.

By definition, the relevant cardinal energy function is distinct from the gravitational potential energy of the system as a whole; the latter may also change as a result of gravitational work done by the surroundings on the system. The gravitational potential energy of the system is a component of its total energy, alongside its other components, namely its cardinal thermodynamic (e.g. internal) energy and its kinetic energy as a whole system in motion.

See also

• Electrochemical hydrogen compressor
• Chemical reactions
• Microstate (statistical mechanics) - includes Microscopic definition of work