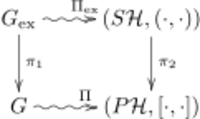Physics:Lie algebra extension
| Group theory → Lie groups Lie groups |
|---|
 |
In the theory of Lie groups, Lie algebras and their representation theory, a Lie algebra extension e is an enlargement of a given Lie algebra g by another Lie algebra h. Extensions arise in several ways. There is the trivial extension obtained by taking a direct sum of two Lie algebras. Other types are the split extension and the central extension. Extensions may arise naturally, for instance, when forming a Lie algebra from projective group representations. Such a Lie algebra will contain central charges.
Starting with a polynomial loop algebra over finite-dimensional simple Lie algebra and performing two extensions, a central extension and an extension by a derivation, one obtains a Lie algebra which is isomorphic with an untwisted affine Kac–Moody algebra. Using the centrally extended loop algebra one may construct a current algebra in two spacetime dimensions. The Virasoro algebra is the universal central extension of the Witt algebra.[1]
Central extensions are needed in physics, because the symmetry group of a quantized system usually is a central extension of the classical symmetry group, and in the same way the corresponding symmetry Lie algebra of the quantum system is, in general, a central extension of the classical symmetry algebra.[2] Kac–Moody algebras have been conjectured to be symmetry groups of a unified superstring theory.[3] The centrally extended Lie algebras play a dominant role in quantum field theory, particularly in conformal field theory, string theory and in M-theory.[4][5]
A large portion towards the end is devoted to background material for applications of Lie algebra extensions, both in mathematics and in physics, in areas where they are actually useful. A parenthetical link, (background material), is provided where it might be beneficial.
History
Due to the Lie correspondence, the theory, and consequently the history of Lie algebra extensions, is tightly linked to the theory and history of group extensions. A systematic study of group extensions was performed by the Austrian mathematician Otto Schreier in 1923 in his PhD thesis and later published.[nb 1][6][7] The problem posed for his thesis by Otto Hölder was "given two groups G and H, find all groups E having a normal subgroup N isomorphic to G such that the factor group E/N is isomorphic to H".
Lie algebra extensions are most interesting and useful for infinite-dimensional Lie algebras. In 1967, Victor Kac and Robert Moody independently generalized the notion of classical Lie algebras, resulting in a new theory of infinite-dimensional Lie algebras, now called Kac–Moody algebras.[8][9] They generalize the finite-dimensional simple Lie algebras and can often concretely be constructed as extensions.[10]
Notation and proofs
Notational abuse to be found below includes eX for the exponential map exp given an argument, writing g for the element (g, eH) in a direct product G × H (eH is the identity in H), and analogously for Lie algebra direct sums (where also g + h and (g, h) are used interchangeably). Likewise for semidirect products and semidirect sums. Canonical injections (both for groups and Lie algebras) are used for implicit identifications. Furthermore, if G, H, ..., are groups, then the default names for elements of G, H, ..., are g, h, ..., and their Lie algebras are g, h, ... . The default names for elements of g, h, ..., are G, H, ... (just like for the groups!), partly to save scarce alphabetical resources but mostly to have a uniform notation.
Lie algebras that are ingredients in an extension will, without comment, be taken to be over the same field.
The summation convention applies, including sometimes when the indices involved are both upstairs or both downstairs.
Caveat: Not all proofs and proof outlines below have universal validity. The main reason is that the Lie algebras are often infinite-dimensional, and then there may or may not be a Lie group corresponding to the Lie algebra. Moreover, even if such a group exists, it may not have the "usual" properties, e.g. the exponential map might not exist, and if it does, it might not have all the "usual" properties. In such cases, it is questionable whether the group should be endowed with the "Lie" qualifier. The literature is not uniform. For the explicit examples, the relevant structures are supposedly in place.
Definition
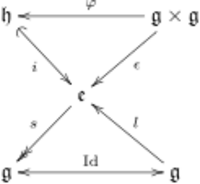
Lie algebra extensions are formalized in terms of short exact sequences.[1] A short exact sequence is an exact sequence of length three,
-
[math]\displaystyle{ \mathfrak h \; \overset i \hookrightarrow \; \mathfrak e \; \overset s \twoheadrightarrow \; \mathfrak g, }[/math]
()
such that i is a monomorphism, s is an epimorphism, and ker s = im i. From these properties of exact sequences, it follows that (the image of) h is an ideal in e. Moreover,
- [math]\displaystyle{ \mathfrak g \cong \mathfrak e/\operatorname{Im} i = \mathfrak e/ \operatorname{Ker} s, }[/math]
but it is not necessarily the case that g is isomorphic to a subalgebra of e. This construction mirrors the analogous constructions in the closely related concept of group extensions.
If the situation in (1) prevails, non-trivially and for Lie algebras over the same field, then one says that e is an extension of g by h.
Properties
The defining property may be reformulated. The Lie algebra e is an extension of g by h if
-
[math]\displaystyle{ 0 \; \overset \iota \hookrightarrow \mathfrak h \; \overset i \hookrightarrow \; \mathfrak e \; \overset s \twoheadrightarrow \; \mathfrak g \; \overset \sigma \twoheadrightarrow \; 0 }[/math]
()
is exact. Here the zeros on the ends represent the zero Lie algebra (containing only the zero vector 0) and the maps are the obvious ones; ί maps 0 to 0 and σ maps all elements of g to 0. With this definition, it follows automatically that i is a monomorphism and s is an epimorphism.
An extension of g by h is not necessarily unique. Let e, e' denote two extensions and let the primes below have the obvious interpretation. Then, if there exists a Lie algebra isomorphism f:e → e' such that
- [math]\displaystyle{ f \circ i = i', \quad s' \circ f = s, }[/math]
then the extensions e and e' are said to be equivalent extensions. Equivalence of extensions is an equivalence relation.
Extension types
Trivial
A Lie algebra extension
- [math]\displaystyle{ \mathfrak h \; \overset i \hookrightarrow \; \mathfrak t \; \overset s \twoheadrightarrow \; \mathfrak g, }[/math]
is trivial if there is a subspace i such that t = i ⊕ ker s and i is an ideal in t.[1]
Split
A Lie algebra extension
- [math]\displaystyle{ \mathfrak h \; \overset i \hookrightarrow \; \mathfrak s \; \overset s \twoheadrightarrow \; \mathfrak g, }[/math]
is split if there is a subspace u such that s = u ⊕ ker s as a vector space and u is a subalgebra in s.
An ideal is a subalgebra, but a subalgebra is not necessarily an ideal. A trivial extension is thus a split extension.
Central
Central extensions of a Lie algebra g by an abelian Lie algebra e can be obtained with the help of a so-called (nontrivial) 2-cocycle (background) on g. Non-trivial 2-cocycles occur in the context of projective representations (background) of Lie groups. This is alluded to further down.
A Lie algebra extension
- [math]\displaystyle{ \mathfrak h \; \overset i \hookrightarrow \; \mathfrak e \; \overset s \twoheadrightarrow \; \mathfrak g, }[/math]
is a central extension if ker s is contained in the center Z(e) of e.
Properties
- Since the center commutes with everything, h ≅ im i = ker s in this case is abelian.
- Given a central extension e of g, one may construct a 2-cocycle on g. Suppose e is a central extension of g by h. Let l be a linear map from g to e with the property that s ∘ l = Idg, i.e. l is a section of s. Use this section to define ε: g × g → e by
- [math]\displaystyle{ \epsilon(G_1, G_2) = l([G_1, G_2]) - [l(G_1), l(G_2)], \quad G_1, G_2 \in \mathfrak g. }[/math]
The map ε satisfies
- [math]\displaystyle{ \epsilon(G_1, [G_2, G_3]) + \epsilon(G_2, [G_3, G_1]) + \epsilon(G_3, [G_1, G_2]) = 0 \in \mathfrak e. }[/math]
To see this, use the definition of ε on the left hand side, then use the linearity of l. Use Jacobi identity on g to get rid of half of the six terms. Use the definition of ε again on terms l([Gi,Gj]) sitting inside three Lie brackets, bilinearity of Lie brackets, and the Jacobi identity on e, and then finally use on the three remaining terms that Im ε ⊂ ker s and that ker s ⊂ Z(e) so that ε(Gi, Gj) brackets to zero with everything. It then follows that φ = i−1 ∘ ε satisfies the corresponding relation, and if h in addition is one-dimensional, then φ is a 2-cocycle on g (via a trivial correspondence of h with the underlying field).
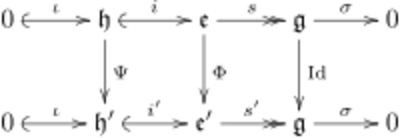
A central extension
- [math]\displaystyle{ 0 \; \overset \iota \hookrightarrow \mathfrak h \; \overset i \hookrightarrow \; \mathfrak e \; \overset s \twoheadrightarrow \; \mathfrak g \; \overset \sigma \twoheadrightarrow \; 0 }[/math]
is universal if for every other central extension
- [math]\displaystyle{ 0 \; \overset \iota \hookrightarrow \mathfrak h' \; \overset {i'} \hookrightarrow \; \mathfrak e' \; \overset {s'} \twoheadrightarrow \; \mathfrak g \; \overset \sigma \twoheadrightarrow \; 0 }[/math]
there exist unique homomorphisms [math]\displaystyle{ \Phi : \mathfrak e \to \mathfrak e' }[/math] and [math]\displaystyle{ \Psi : \mathfrak h \to \mathfrak h' }[/math] such that the diagram
commutes, i.e. i' ∘ Ψ = Φ ∘ i and s' ∘ Φ = s. By universality, it is easy to conclude that such universal central extensions are unique up to isomorphism.
Construction
By direct sum
Let [math]\displaystyle{ \mathfrak g }[/math], [math]\displaystyle{ \mathfrak h }[/math] be Lie algebras over the same field [math]\displaystyle{ F }[/math]. Define
- [math]\displaystyle{ \mathfrak e = \mathfrak h \times \mathfrak g, }[/math]
and define addition pointwise on [math]\displaystyle{ \mathfrak e }[/math]. Scalar multiplication is defined by
- [math]\displaystyle{ \alpha(H, G) = (\alpha H, \alpha G), \alpha \in F, H \in \mathfrak h, G \in \mathfrak g. }[/math]
With these definitions, [math]\displaystyle{ \mathfrak h \times \mathfrak g \equiv \mathfrak h \oplus \mathfrak g }[/math] is a vector space over [math]\displaystyle{ F }[/math]. With the Lie bracket:
-
[math]\displaystyle{ [(H_1, G_1),(H_2, G_2)] = ([H_1, H_2],[G_1, G_2]), }[/math]
()
[math]\displaystyle{ \mathfrak e }[/math] is a Lie algebra. Define further
- [math]\displaystyle{ i:\mathfrak h \hookrightarrow \mathfrak e; H \mapsto (H, 0), \quad s:\mathfrak e \twoheadrightarrow \mathfrak g; (H, G) \mapsto G. }[/math]
It is clear that (1) holds as an exact sequence. This extension of [math]\displaystyle{ \mathfrak g }[/math] by [math]\displaystyle{ \mathfrak h }[/math] is called a trivial extension. It is, of course, nothing else than the Lie algebra direct sum. By symmetry of definitions, [math]\displaystyle{ \mathfrak e }[/math] is an extension of [math]\displaystyle{ \mathfrak h }[/math] by [math]\displaystyle{ \mathfrak g }[/math] as well, but [math]\displaystyle{ \mathfrak h \oplus \mathfrak g \neq \mathfrak g \oplus \mathfrak h }[/math]. It is clear from (3) that the subalgebra [math]\displaystyle{ 0 \oplus \mathfrak g }[/math] is an ideal (Lie algebra). This property of the direct sum of Lie algebras is promoted to the definition of a trivial extension.
By semidirect sum
Inspired by the construction of a semidirect product (background) of groups using a homomorphism G → Aut(H), one can make the corresponding construct for Lie algebras.
If ψ:g → Der h is a Lie algebra homomorphism, then define a Lie bracket on [math]\displaystyle{ \mathfrak e = \mathfrak h \oplus \mathfrak g }[/math] by
-
[math]\displaystyle{ [(H , G), (H' , G')] = ([H , H'] + \psi_G(H') - \psi_{G'}(H), [G , G']),\quad H,H' \in \mathfrak h, G, G' \in \mathfrak g. }[/math]
()
With this Lie bracket, the Lie algebra so obtained is denoted e= h ⊕S g and is called the semidirect sum of h and g.
By inspection of (7) one sees that 0 ⊕ g is a subalgebra of e and h ⊕ 0 is an ideal in e. Define i:h → e by H ↦ H ⊕ 0 and s:e → g by H ⊕ G ↦ G, H ∈ h, G ∈ g. It is clear that ker s = im i. Thus e is a Lie algebra extension of g by h.
As with the trivial extension, this property generalizes to the definition of a split extension.
Example
Let G be the Lorentz group O(3, 1) and let T denote the translation group in 4 dimensions, isomorphic to ([math]\displaystyle{ \mathbb{R}^4 }[/math], +), and consider the multiplication rule of the Poincaré group P
- [math]\displaystyle{ (a_2, \Lambda_2)(a_1, \Lambda_1) = (a_2 + \Lambda_2a_1, \Lambda_2\Lambda_1), \quad a_1, a_2 \in \mathrm T \subset \mathrm P, \Lambda_1, \Lambda_2 \in \mathrm O(3,1) \subset \mathrm P, }[/math]
(where T and O(3, 1) are identified with their images in P). From it follows immediately that, in the Poincaré group, (0, Λ)(a, I)(0, Λ−1) = (Λ a, I) ∈ T ⊂ P. Thus every Lorentz transformation Λ corresponds to an automorphism ΦΛ of T with inverse ΦΛ−1 and Φ is clearly a homomorphism. Now define
- [math]\displaystyle{ \overline \mathrm P = \mathrm T \otimes_S \mathrm O(3, 1), }[/math]
endowed with multiplication given by (4). Unwinding the definitions one finds that the multiplication is the same as the multiplication one started with and it follows that P = P. From (5') follows that ΨΛ = AdΛ and then from (6') it follows that ψλ = adλ. λ ∈ o(3, 1).
By derivation
Let δ be a derivation (background) of h and denote by g the one-dimensional Lie algebra spanned by δ. Define the Lie bracket on e = g ⊕ h by[nb 2][11]
- [math]\displaystyle{ [G_1 + H_1, G_2 + H_2] = [\lambda\delta + H_1, \mu\delta + H_2] = [H_1, H_2] + \lambda \delta(H_1) - \mu \delta(H_2). }[/math]
It is obvious from the definition of the bracket that h is and ideal in e in and that g is a subalgebra of e. Furthermore, g is complementary to h in e. Let i:h → e be given by H ↦ (0, H) and s:e → g by (G, H) ↦ G. It is clear that im i = ker s. Thus e is a split extension of g by h. Such an extension is called extension by a derivation.
If ψ: g → der h is defined by ψ(μδ)(H) = μδ(H), then ψ is a Lie algebra homomorphism into der h. Hence this construction is a special case of a semidirect sum, for when starting from ψ and using the construction in the preceding section, the same Lie brackets result.
By 2-cocycle
If ε is a 2-cocycle (background) on a Lie algebra g and h is any one-dimensional vector space, let e = h ⊕ g (vector space direct sum) and define a Lie bracket on e by
- [math]\displaystyle{ [\mu H + G_1, \nu H + G_2] = [G_1, G_2] + \epsilon(G_1, G_2)H, \quad \mu, \nu \in F. }[/math]
Here H is an arbitrary but fixed element of h. Antisymmetry follows from antisymmetry of the Lie bracket on g and antisymmetry of the 2-cocycle. The Jacobi identity follows from the corresponding properties of g and of ε. Thus e is a Lie algebra. Put G1 = 0 and it follows that μH ∈ Z(e). Also, it follows with i: μH ↦ (μH, 0) and s: (μH, G) ↦ G that Im i = ker s = {(μH, 0):μ ∈ F} ⊂ Z(e). Hence e is a central extension of g by h. It is called extension by a 2-cocycle.
Theorems
Below follows some results regarding central extensions and 2-cocycles.[12]
Theorem[1]
Let φ1 and φ2 be cohomologous 2-cocycles on a Lie algebra g and let e1 and e2 be respectively the central extensions constructed with these 2-cocycles. Then the central extensions e1 and e2 are equivalent extensions.
Proof
By definition, φ2 = φ1 + δf. Define
- [math]\displaystyle{ \psi: G + \mu c \in \mathfrak{e}_1 \mapsto G + \mu c + f(G)c \in \mathfrak{e}_2. }[/math]
It follows from the definitions that ψ is a Lie algebra isomorphism and (2) holds.
Corollary
A cohomology class [Φ] ∈ H2(g, F) defines a central extension of g which is unique up to isomorphism.
The trivial 2-cocycle gives the trivial extension, and since a 2-coboundary is cohomologous with the trivial 2-cocycle, one has
Corollary
A central extension defined by a coboundary is equivalent with a trivial central extension.
Theorem
A finite-dimensional simple Lie algebra has only trivial central extensions.
Proof
Since every central extension comes from a 2-cocycle φ, it suffices to show that every 2-cocycle is a coboundary. Suppose φ is a 2-cocycle on g. The task is to use this 2-cocycle to manufacture a 1-cochain f such that φ = δf.
The first step is to, for each G1 ∈ g, use φ to define a linear map ρG1:g → F by [math]\displaystyle{ \rho_{G_1}(G_2) \equiv \varphi(G_1, G_2) }[/math]. These linear maps are elements of g∗. Let ν:g∗ →g be the vector space isomorphism associated to the nondegenerate Killing form K, and define a linear map d:g → g by [math]\displaystyle{ d(G_1) \equiv \nu(\rho_{G_1}) }[/math]. This turns out to be a derivation (for a proof, see below). Since, for semisimple Lie algebras, all derivations are inner, one has d = adGd for some Gd ∈ g. Then
- [math]\displaystyle{ \varphi(G_1, G_2) \equiv \rho_{G_1}(G_2) = K(\nu(\rho_{G_1}), G_2) \equiv K(d(G_1), G_2) = K(\mathrm{ad}_{G_d}(G_1), G_2) = K([G_d, G_1], G_2) = K(G_d, [G_1, G_2]). }[/math]
Let f be the 1-cochain defined by
- [math]\displaystyle{ f(G) = K(G_d,G). }[/math]
Then
- [math]\displaystyle{ \delta f(G_1, G_2) = f([G_1, G_2]) = K(G_d,[G_1, G_2]) = \varphi(G_1, G_2), }[/math]
showing that φ is a coboundary.
To verify that d actually is a derivation, first note that it is linear since ν is, then compute
- [math]\displaystyle{ \begin{align}K(d([G_1, G_2]), G_3)) &= \varphi([G_1, G_2]), G_3)) = \varphi(G_1,[G_2, G_3]) + \varphi(G_2, [G_3, G_1])\\ &= K(d(G_1),[G_2, G_3]) + K(d(G_1), (G_3, G_1)) = K([d(G_1),G_2], G_3) + K([G_1, d(G_2)], G_3))\\ &= K([d(G_1), G_2] + [G_1, d(G_2)], G_3).\end{align} }[/math]
By appeal to the non-degeneracy of K, the left arguments of K are equal on the far left and far right.
The observation that one can define a derivation d, given a symmetric non-degenerate associative form K and a 2-cocycle φ, by
- [math]\displaystyle{ K(\nu(\rho_{G_1}), G_2) \equiv K(d(G_1), G_2), }[/math]
or using the symmetry of K and the antisymmetry of φ,
- [math]\displaystyle{ K(d(G_1), G_2) = -K(G_1, d(G_2)), }[/math]
leads to a corollary.
Corollary
Let L:'g × g: → F be a non-degenerate symmetric associative bilinear form and let d be a derivation satisfying
- [math]\displaystyle{ L(d(G_1), G_2) = -L(G_1, d(G_2)), }[/math]
then φ defined by
- [math]\displaystyle{ \varphi(G_1, G_2) = L(d(G_1), G_2) }[/math]
is a 2-cocycle.
Proof The condition on d ensures the antisymmetry of φ. The Jacobi identity for 2-cocycles follows starting with
- [math]\displaystyle{ \varphi([G1, G_2], G_3) = L(d[G1, G_2], G_3) = L([d(G1), G_2], G_3) + L([G1, d(G_2)], G_3), }[/math]
using symmetry of the form, the antisymmetry of the bracket, and once again the definition of φ in terms of L.
If g is the Lie algebra of a Lie group G and e is a central extension of g, one may ask whether there is a Lie group E with Lie algebra e. The answer is, by Lie's third theorem affirmative. But is there a central extension E of G with Lie algebra e? The answer to this question requires some machinery, and can be found in (Tuynman Wiegerinck).
Applications
The "negative" result of the preceding theorem indicates that one must, at least for semisimple Lie algebras, go to infinite-dimensional Lie algebras to find useful applications of central extensions. There are indeed such. Here will be presented affine Kac–Moody algebras and Virasoro algebras. These are extensions of polynomial loop-algebras and the Witt algebra respectively.
Polynomial loop-algebra
Let g be a polynomial loop algebra (background),
- [math]\displaystyle{ \mathfrak g = \mathbb{C}[\lambda, \lambda^{-1}] \otimes \mathfrak g_0, }[/math]
where g0 is a complex finite-dimensional simple Lie algebra. The goal is to find a central extension of this algebra. Two of the theorems apply. On the one hand, if there is a 2-cocycle on g, then a central extension may be defined. On the other hand, if this 2-cocycle is acting on the g0 part (only), then the resulting extension is trivial. Moreover, derivations acting on g0 (only) cannot be used for definition of a 2-cocycle either because these derivations are all inner and the same problem results. One therefore looks for derivations on C[λ, λ−1]. One such set of derivations is
- [math]\displaystyle{ d_k \equiv \lambda^{k+1}\frac{d}{d\lambda}, \quad k \in \mathbb Z. }[/math]
In order to manufacture a non-degenerate bilinear associative antisymmetric form L on g, attention is focused first on restrictions on the arguments, with m, n fixed. It is a theorem that every form satisfying the requirements is a multiple of the Killing form K on g0.[13] This requires
- [math]\displaystyle{ L(\lambda^m \otimes G_1, \lambda^n \otimes G_2) = \gamma_{lm}K(G_1, G_2). }[/math]
Symmetry of K implies
- [math]\displaystyle{ \gamma_{mn}=\gamma_{nm}, }[/math]
and associativity yields
- [math]\displaystyle{ \gamma_{m+k,n}=\gamma_{m,k+n}. }[/math]
With m = 0 one sees that γk,n = γ0,k+n. This last condition implies the former. Using this fact, define f(n) = γ0,n. The defining equation then becomes
- [math]\displaystyle{ L(\lambda^m \otimes G_1, \lambda^n \otimes G_2) = f(m+n)K(G_1, G_2). }[/math]
For every i ∈ [math]\displaystyle{ \mathbb{Z} }[/math] the definition
- [math]\displaystyle{ f(n) = \delta_{ni} \Leftrightarrow \gamma_{mn}=\delta_{m+n, i} }[/math]
does define a symmetric associative bilinear form
- [math]\displaystyle{ L_i(\lambda^m \otimes G_1, \lambda^n \otimes G_2) = \delta_{m+n,i}K(G_1, G_2). }[/math]
These span a vector space of forms which have the right properties.
Returning to the derivations at hand and the condition
- [math]\displaystyle{ L_i(d_k(\lambda^l \otimes G_1), \lambda^m \otimes G_2) = -L_i(\lambda^l \otimes G_1, d_k(\lambda^m \otimes G_2)), }[/math]
one sees, using the definitions, that
- [math]\displaystyle{ l\delta_{k+l+m,i} = -m\delta_{k+l+m,i}, }[/math]
or, with n = l + m,
- [math]\displaystyle{ n\delta_{k+n,i} = 0. }[/math]
This (and the antisymmetry condition) holds if k = i, in particular it holds when k = i = 0.
Thus choose L = L0 and d = d0. With these choices, the premises in the corollary are satisfied. The 2-cocycle φ defined by
- [math]\displaystyle{ \varphi(P(\lambda) \otimes G_1), Q(\lambda) \otimes G_2)) = L(\lambda\frac{dP}{d\lambda} \otimes G_1, Q(\lambda) \otimes G_2) }[/math]
is finally employed to define a central extension of g,
- [math]\displaystyle{ \mathfrak e = \mathfrak g \oplus \mathbb CC, }[/math]
with Lie bracket
- [math]\displaystyle{ [P(\lambda) \otimes G_1 + \mu C, Q(\lambda) \otimes G_2 + \nu C] = P(\lambda)Q(\lambda)\otimes[G_1, G_2] + \varphi(P(\lambda) \otimes G_1,Q(\lambda) \otimes G_2)C. }[/math]
For basis elements, suitably normalized and with antisymmetric structure constants, one has
- [math]\displaystyle{ \begin{align}{}[\lambda^l \otimes G_i + \mu C, \lambda^m \otimes G_j + \nu C] &= \lambda^{l+m}\otimes[G_i, G_j] + \varphi(\lambda^l \otimes G_i,\lambda^m \otimes G_j)C\\ &= \lambda^{l+m}\otimes {C_{ij}}^kG_k + L(\lambda \frac{d\lambda^l}{d\lambda} \otimes G_i, \lambda^m \otimes G_j)C\\ &=\lambda^{l+m}\otimes {C_{ij}}^kG_k + lL(\lambda^l \otimes G_i, \lambda^m \otimes G_j)C\\ &=\lambda^{l+m}\otimes {C_{ij}}^kG_k + l\delta_{l+m, 0}K(G_i, G_j)C\\ &=\lambda^{l+m}\otimes {C_{ij}}^kG_k + l\delta_{l+m, 0}{C_{ik}}^m{C_{jm}}^kC = \lambda^{l+m}\otimes {C_{ij}}^kG_k + l\delta_{l+m, 0}\delta^{ij}C. \end{align} }[/math]
This is a universal central extension of the polynomial loop algebra.[14]
- A note on terminology
In physics terminology, the algebra of above might pass for a Kac–Moody algebra, whilst it will probably not in mathematics terminology. An additional dimension, an extension by a derivation is required for this. Nonetheless, if, in a physical application, the eigenvalues of g0 or its representative are interpreted as (ordinary) quantum numbers, the additional superscript on the generators is referred to as the level. It is an additional quantum number. An additional operator whose eigenvalues are precisely the levels is introduced further below.
Current algebra

As an application of a central extension of polynomial loop algebra, a current algebra of a quantum field theory is considered (background). Suppose one has a current algebra, with the interesting commutator being
-
[math]\displaystyle{ [J_a^0(t, \mathbf x), J_b^i(t, \mathbf y)] = i{C_{ab}}^cJ_c^i(t, \mathbf x)\delta(\mathbf x - \mathbf y) + S_{ab}^{ij}\partial_j\delta(\mathbf x - \mathbf y) + ... , }[/math]
()
with a Schwinger term. To construct this algebra mathematically, let g be the centrally extended polynomial loop algebra of the previous section with
- [math]\displaystyle{ [\lambda^l \otimes G_i + \mu C, \lambda^m \otimes G_j + \nu C] = \lambda^{l+m}\otimes {C_{ij}}^kG_k + l\delta_{l+m, 0}\delta_{ij}C }[/math]
as one of the commutation relations, or, with a switch of notation (l→m, m→n, i→a, j→b, λm⊗Ga→Tma) with a factor of i under the physics convention,[nb 3]
- [math]\displaystyle{ [T^m_a, T^n_b] = i{C_{ab}}^cT^{m+n}_c + m\delta_{m+n, 0}\delta_{ab}C. }[/math]
Define using elements of g,
- [math]\displaystyle{ J_a(x) = \frac{\hbar}{L}\sum_{n=-\infty}^{\infty}e^{\frac{2\pi inx}{L}}T_a^{-n}, x \in \mathbb R. }[/math]
One notes that
- [math]\displaystyle{ J_a(x+L) = J_a(x) }[/math]
so that it is defined on a circle. Now compute the commutator,
- [math]\displaystyle{ \begin{align}[] [J_a(x),J_b(y)]&= \left(\frac{\hbar}{L}\right)^2\left[\sum_{n=-\infty}^{\infty}e^{\frac{2\pi inx}{L}}T_a^{-n}, \sum_{m=-\infty}^{\infty}e^{\frac{2\pi imy}{L}}T_b^{-m}\right]\\ &=\left(\frac{\hbar}{L}\right)^2 \sum_{m,n=-\infty}^{\infty} e^{\frac{2\pi inx}{L}} e^{\frac{2\pi imy}{L}} [T_a^{-n},T_b^{-m}].\end{align} }[/math]
For simplicity, switch coordinates so that y → 0, x → x − y ≡ z and use the commutation relations,
- [math]\displaystyle{ \begin{align}[] [J_a(z),J_b(0)] &= \left(\frac{\hbar}{L}\right)^2\sum_{m,n=-\infty}^{\infty} e^{\frac{2\pi inz}{L}}[i{C_{ab}}^cT^{-m-n}_c + m\delta_{m+n, 0}\delta_{ab}C]\\ &=\left(\frac{\hbar}{L}\right)^2\sum_{m=-\infty}^{\infty} e^{\frac{2\pi i(-m)z}{L}}\sum_{l=-\infty}^\infty ie^{\frac{2\pi i(l)z}{L}}{C_{ab}}^cT^{-l}_c + \left(\frac{\hbar}{L}\right)^2\sum_{m,n=-\infty}^{\infty}e^{\frac{2\pi inz}{L}}m\delta_{m+n, 0}\delta_{ab}C\\ &=\left(\frac{\hbar}{L}\right)\sum_{m=-\infty}^{\infty} e^{\frac{2\pi imz}{L}}i{C_{ab}}^cJ_c(z) - \left(\frac{\hbar}{L}\right)^2\sum_{n=-\infty}^{\infty}e^{\frac{2\pi inz}{L}}n\delta_{ab}C\end{align} }[/math]
Now employ the Poisson summation formula,
- [math]\displaystyle{ \frac{1}{L}\sum_{n=-\infty}^\infty e^{\frac{-2\pi inz}{L}} = \frac{1}{L}\sum_{n=-\infty}^\infty \delta(z + nL) = \delta(z) }[/math]
for z in the interval (0, L) and differentiate it to yield
- [math]\displaystyle{ -\frac{2\pi i}{L^2}\sum_{n=-\infty}^\infty ne^{\frac{-2\pi inz}{L}} = \delta'(z), }[/math]
and finally
- [math]\displaystyle{ [J_a(x-y),J_b(0)] = i\hbar {C_{ab}}^cJ_c(x-y)\delta(x-y) + \frac{i\hbar^2}{2\pi}\delta_{ab}C\delta'(x-y), }[/math]
or
- [math]\displaystyle{ [J_a(x),J_b(y)] = i\hbar {C_{ab}}^cJ_c(x)\delta(x-y) + \frac{i\hbar^2}{2\pi}\delta_{ab}C\delta'(x-y), }[/math]
since the delta functions arguments only ensure that the arguments of the left and right arguments of the commutator are equal (formally δ(z) = δ(z − 0) ↦ δ((x −y) − 0) = δ(x −y)).
By comparison with CA10, this is a current algebra in two spacetime dimensions, including a Schwinger term, with the space dimension curled up into a circle. In the classical setting of quantum field theory, this is perhaps of little use, but with the advent of string theory where fields live on world sheets of strings, and spatial dimensions are curled up, there may be relevant applications.
Kac–Moody algebra
The derivation d0 used in the construction of the 2-cocycle φ in the previous section can be extended to a derivation D on the centrally extended polynomial loop algebra, here denoted by g in order to realize a Kac–Moody algebra[15][16] (background). Simply set
- [math]\displaystyle{ D(P(\lambda) \otimes G + \mu C) = \lambda \frac{dP(\lambda)}{d\lambda} \otimes G. }[/math]
Next, define as a vector space
- [math]\displaystyle{ \mathfrak e = \mathbb Cd + \mathfrak g. }[/math]
The Lie bracket on e is, according to the standard construction with a derivation, given on a basis by
- [math]\displaystyle{ \begin{align}{}[\lambda^m \otimes G_1 + \mu C + \nu D, \lambda^n \otimes G_2 + \mu' C + \nu' D] &= \lambda^{m+n} \otimes [G_1, G_2] + m\delta_{m+n,0}K(G_1, G_2)C + \nu D(\lambda^n \otimes G_1) - \nu'D(\lambda^m \otimes G_2)\\ &= \lambda^{m+n} \otimes [G_1, G_2] + m\delta_{m+n,0}K(G_1, G_2)C + \nu n\lambda^n \otimes G_1 - \nu'm \lambda^m \otimes G_2.\end{align} }[/math]
For convenience, define
- [math]\displaystyle{ G_i^m \leftrightarrow \lambda^m \otimes G_i. }[/math]
In addition, assume the basis on the underlying finite-dimensional simple Lie algebra has been chosen so that the structure coefficients are antisymmetric in all indices and that the basis is appropriately normalized. Then one immediately through the definitions verifies the following commutation relations.
- [math]\displaystyle{ \begin{align}{}[G_i^m,G_j^n] &= {C_{ij}}^kG_k^{m+n} + m\delta_{ij}\delta^{m+n,0}C,\\ {}[C,G_i^m] &= 0, \quad 1 \le i, j, N,\quad m,n \in \mathbb Z\\ {}[D, G_i^m] &= mG_i^m\\ {}[D,C] &= 0.\end{align} }[/math]
These are precisely the short-hand description of an untwisted affine Kac–Moody algebra. To recapitulate, begin with a finite-dimensional simple Lie algebra. Define a space of formal Laurent polynomials with coefficients in the finite-dimensional simple Lie algebra. With the support of a symmetric non-degenerate alternating bilinear form and a derivation, a 2-cocycle is defined, subsequently used in the standard prescription for a central extension by a 2-cocycle. Extend the derivation to this new space, use the standard prescription for a split extension by a derivation and an untwisted affine Kac–Moody algebra obtains.
Virasoro algebra
The purpose is to construct the Virasoro algebra (named after Miguel Angel Virasoro)[nb 4] as a central extension by a 2-cocycle φ of the Witt algebra W (background). The Jacobi identity for 2-cocycles yields
-
[math]\displaystyle{ (l-m)\eta_{n+m,p} + (m-n)\eta_{m+n,l} + (n-l)\eta_{l+n,m} = 0, \quad \eta_{ij} = \varphi(d_i, d_j). }[/math]
()
Letting [math]\displaystyle{ l = 0 }[/math] and using antisymmetry of η one obtains
- [math]\displaystyle{ (m+p)\eta_{mp}=(m-p)\eta_{m+p,0}. }[/math]
In the extension, the commutation relations for the element d0 are
- [math]\displaystyle{ [d_0 + \mu C, d_m + \nu C]_\varphi = -md_m + \eta_{0m}C = -m(d_m - \frac{\eta_{0m}}{m}C). }[/math]
It is desirable to get rid of the central charge on the right hand side. To do this define
- [math]\displaystyle{ f:W \to \mathbb C; d_m \to \frac{\varphi(d_0,d_m)}{m} = \frac{\eta_{0m}}{m}. }[/math]
Then, using f as a 1-cochain,
- [math]\displaystyle{ \eta'_{0n} = \varphi'(d_0, d_n) = \varphi(d_0, d_n) + \delta f([d_0, d_n]) = \varphi(d_0, d_n) -n \frac{\eta^{0n}}{n}= 0, }[/math]
so with this 2-cocycle, equivalent to the previous one, one has[nb 5]
- [math]\displaystyle{ [d_0 + \mu C, d_m + \nu C]_{\varphi'} = -md_m. }[/math]
With this new 2-cocycle (skip the prime) the condition becomes
- [math]\displaystyle{ (n+p)\eta_{mp} = (n-p)\eta_{m+p,0}=0, }[/math]
and thus
- [math]\displaystyle{ \eta_{mp}=a(m)\delta_{m. -p}, \quad a(-m) = -a(m), }[/math]
where the last condition is due to the antisymmetry of the Lie bracket. With this, and with l + m + p = 0 (cutting out a "plane" in [math]\displaystyle{ \mathbb{Z}^3 }[/math]), (V10) yields
- [math]\displaystyle{ (2m+p)a(p) + (m-p)a(m+p) + (m+2p)a(m) = 0, }[/math]
that with p = 1 (cutting out a "line" in [math]\displaystyle{ \mathbb{Z}^2 }[/math]) becomes
- [math]\displaystyle{ (m-1)a(m+1) - (m+2)a(m) + (2m+1)a(1) = 0. }[/math]
This is a difference equation generally solved by
- [math]\displaystyle{ a(m) = \alpha m + \beta m^3. }[/math]
The commutator in the extension on elements of W is then
- [math]\displaystyle{ [d_l, d_m] = (l-m)d_{l+m} + (\alpha m + \beta m^3)\delta_{l,-m}C. }[/math]
With β = 0 it is possible to change basis (or modify the 2-cocycle by a 2-coboundary) so that
- [math]\displaystyle{ [d'_l, d'_m] = (l-m)d_{l+m}, }[/math]
with the central charge absent altogether, and the extension is hence trivial. (This was not (generally) the case with the previous modification, where only d0 obtained the original relations.) With β ≠ 0 the following change of basis,
- [math]\displaystyle{ d'_l = d_l + \delta_{0l}\frac{\alpha+\gamma}{2}C, }[/math]
the commutation relations take the form
- [math]\displaystyle{ [d'_l, d'_m] = (l-m)d'_{l+m} + (\gamma m + \beta m^3)\delta_{l,-m}C, }[/math]
showing that the part linear in m is trivial. It also shows that H2(W, [math]\displaystyle{ \mathbb{C} }[/math]) is one-dimensional (corresponding to the choice of β). The conventional choice is to take α = −β = 1⁄12 and still retaining freedom by absorbing an arbitrary factor in the arbitrary object C. The Virasoro algebra V is then
- [math]\displaystyle{ \mathcal V = \mathcal W + \mathbb C C, }[/math]
with commutation relations
[math]\displaystyle{ [d_l + \mu C, d_m + \nu C] = (l-m)d_{l+m} + \frac{(m - m^3)}{12}\delta_{l,-m}C. }[/math]
Bosonic open strings
The relativistic classical open string (background) is subject to quantization. This roughly amounts to taking the position and the momentum of the string and promoting them to operators on the space of states of open strings. Since strings are extended objects, this results in a continuum of operators depending on the parameter σ. The following commutation relations are postulated in the Heisenberg picture.[17]
- [math]\displaystyle{ \begin{align}{}[X^I(\tau, \sigma), \mathcal P^{\tau J}(\tau, \sigma)] &= i\eta^{IJ}\delta(\sigma-\sigma'),\\ {}[x_0^-(\tau),p^+(\tau)] &= -i.\end{align} }[/math]
All other commutators vanish.
Because of the continuum of operators, and because of the delta functions, it is desirable to express these relations instead in terms of the quantized versions of the Virasoro modes, the Virasoro operators. These are calculated to satisfy
- [math]\displaystyle{ [\alpha_m^I, \alpha_n^J] = m\eta^{IJ}\delta_{m+n,0} }[/math]
They are interpreted as creation and annihilation operators acting on Hilbert space, increasing or decreasing the quantum of their respective modes. If the index is negative, the operator is a creation operator, otherwise it is an annihilation operator. (If it is zero, it is proportional to the total momentum operator.) In view of the fact that the light cone plus and minus modes were expressed in terms of the transverse Virasoro modes, one must consider the commutation relations between the Virasoro operators. These were classically defined (then modes) as
- [math]\displaystyle{ L_n = \frac{1}{2}\sum_{p \in \mathbb Z}\alpha_{n-p}^I\alpha_p^I. }[/math]
Since, in the quantized theory, the alphas are operators, the ordering of the factors matter. In view of the commutation relation between the mode operators, it will only matter for the operator L0 (for which m + n = 0). L0 is chosen normal ordered,
- [math]\displaystyle{ L_0 = \frac{1}{2}\alpha_0^I\alpha_0^I + \sum_{p=1}^\infty \alpha_{-p}^I\alpha_p^I, = \alpha' p^Ip^I + \sum_{p=1}^\infty p \alpha_{p}^{I\dagger}\alpha_p^I + c }[/math]
where c is a possible ordering constant. One obtains after a somewhat lengthy calculation[18] the relations
- [math]\displaystyle{ [L_m, L_n] = (m-n)L_{m+n}, \quad m+n\ne 0. }[/math]
If one would allow for m + n = 0 above, then one has precisely the commutation relations of the Witt algebra. Instead one has
- [math]\displaystyle{ [L_m, L_n] = (m-n)L_{m+n} + \frac{D-2}{12}(m^3-m)\delta_{m+n,0},\quad \forall m,n \in \mathbb Z. }[/math]
upon identification of the generic central term as (D − 2) times the identity operator, this is the Virasoro algebra, the universal central extension of the Witt algebra.
The operator L0 enters the theory as the Hamiltonian, modulo an additive constant. Moreover, the Virasoro operators enter into the definition of the Lorentz generators of the theory. It is perhaps the most important algebra in string theory.[19] The consistency of the Lorentz generators, by the way, fixes the spacetime dimensionality to 26. While this theory presented here (for relative simplicity of exposition) is unphysical, or at the very least incomplete (it has, for instance, no fermions) the Virasoro algebra arises in the same way in the more viable superstring theory and M-theory.
Group extension
A projective representation Π(G) of a Lie group G (background) can be used to define a so-called group extension Gex.
In quantum mechanics, Wigner's theorem asserts that if G is a symmetry group, then it will be represented projectively on Hilbert space by unitary or antiunitary operators. This is often dealt with by passing to the universal covering group of G and take it as the symmetry group. This works nicely for the rotation group SO(3) and the Lorentz group O(3, 1), but it does not work when the symmetry group is the Galilean group. In this case one has to pass to its central extension, the Bargmann group,[20] which is the symmetry group of the Schrödinger equation. Likewise, if G = [math]\displaystyle{ \mathbb{R}^2 }[/math], the group of translations in position and momentum space, one has to pass to its central extension, the Heisenberg group.[21]
Let ω be the 2-cocycle on G induced by Π. Define[nb 6]
- [math]\displaystyle{ G_{\mathrm {ex}} = \mathbb C^* \times G = \{(\lambda,g)|\lambda \in \mathbb C, g \in G\} }[/math]
as a set and let the multiplication be defined by
- [math]\displaystyle{ (\lambda_1,g_1)(\lambda_2,g_2) = (\lambda_1\lambda_2\omega(g_1,g_2),g_1g_2). }[/math]
Associativity holds since ω is a 2-cocycle on G. One has for the unit element
- [math]\displaystyle{ (1,e)(\lambda,g) = (\lambda\omega(e,g),g) = (\lambda,g) = (\lambda,g)(1,e), }[/math]
and for the inverse
- [math]\displaystyle{ (\lambda,g)^{-1} = \left(\frac{1}{\lambda \omega(g, g^{-1})}, g^{-1}\right). }[/math]
The set ([math]\displaystyle{ \mathbb{C}^* }[/math], e) is an abelian subgroup of Gex. This means that Gex is not semisimple. The center of G, Z(G) = {z ∈ G|zg = gz ∀g ∈ G} includes this subgroup. The center may be larger.
At the level of Lie algebras it can be shown that the Lie algebra gex of Gex is given by
- [math]\displaystyle{ \mathfrak{g}_{\mathrm{ex}} = \mathbb CC \oplus \mathfrak g, }[/math]
as a vector space and endowed with the Lie bracket
- [math]\displaystyle{ [\mu C + G_1,\nu C + G_2] = [G_1, G_2] + \eta(G_1, G_2)C. }[/math]
Here η is a 2-cocycle on g. This 2-cocycle can be obtained from ω albeit in a highly nontrivial way.[nb 7]
Now by using the projective representation Π one may define a map Πex by
- [math]\displaystyle{ \Pi_{\mathrm{ex}}((\lambda,g)) = \lambda\Pi(g). }[/math]
It has the properties
- [math]\displaystyle{ \Pi_{\mathrm{ex}}((\lambda_1,g_1))\Pi_{\mathrm{ex}}((\lambda_2,g_2))=\lambda_1\lambda_2\Pi(g_1)\Pi(g_2)=\lambda_1\lambda_2\omega(g_1,g_2)\Pi(g_1g_2)=\Pi_{\mathrm{ex}}(\lambda_1\lambda_2\omega(g_1,g_2),g_1g_2) = \Pi_{\mathrm{ex}}((\lambda_1, g_1)(\lambda_2,g_2)), }[/math]
so Πex(Gex) is a bona fide representation of Gex.
In the context of Wigner's theorem, the situation may be depicted as such (replace [math]\displaystyle{ \mathbb{C}^* }[/math] by U(1)); let SH denote the unit sphere in Hilbert space H, and let (·,·) be its inner product. Let PH denote ray space and [·,·] the ray product. Let moreover a wiggly arrow denote a group action. Then the diagram
commutes, i.e.
- [math]\displaystyle{ \pi_2 \circ \Pi_{\mathrm{ex}}((\lambda, g))(\psi) = \Pi \circ \pi(g)(\pi_1(\psi)), \quad \psi \in S\mathcal H. }[/math]
Moreover, in the same way that G is a symmetry of PH preserving [·,·], Gex is a symmetry of SH preserving (·,·). The fibers of π2 are all circles. These circles are left invariant under the action of U(1). The action of U(1) on these fibers is transitive with no fixed point. The conclusion is that SH is a principal fiber bundle over PH with structure group U(1).[21]
Background material
In order to adequately discuss extensions, structure that goes beyond the defining properties of a Lie algebra is needed. Rudimentary facts about these are collected here for quick reference.
Derivations
A derivation δ on a Lie algebra g is a map
- [math]\displaystyle{ \delta: \mathfrak g \rightarrow \mathfrak g }[/math]
such that the Leibniz rule
- [math]\displaystyle{ \delta[G_1, G_2] = [\delta G_1, G_2] + [G_1, \delta G_2] }[/math]
holds. The set of derivations on a Lie algebra g is denoted der g. It is itself a Lie algebra under the Lie bracket
- [math]\displaystyle{ [\delta_1, \delta_2] = \delta_1 \circ \delta_2 - \delta_2 \circ \delta_1. }[/math]
It is the Lie algebra of the group Aut g of automorphisms of g.[22] One has to show
- [math]\displaystyle{ \delta[G_1, G_1] = [\delta G_1, G_2] + [G_1, \delta G_2] \Leftrightarrow e^{t\delta}[G_1,G_2] = [e^{t\delta}G_1, e^{t\delta}G_2], \quad \forall t \in \mathbb R. }[/math]
If the rhs holds, differentiate and set t = 0 implying that the lhs holds. If the lhs holds (A), write the rhs as
- [math]\displaystyle{ [G_1,G_2]\; \overset{?}{=}\; e^{-t\delta}[e^{t\delta}G_1, e^{t\delta}G_2], }[/math]
and differentiate the rhs of this expression. It is, using (A), identically zero. Hence the rhs of this expression is independent of t and equals its value for t = 0, which is the lhs of this expression.
If G ∈ g, then adG, acting by adG1(G2) = [G1, G2], is a derivation. The set adG: G ∈ g is the set of inner derivations on g. For finite-dimensional simple Lie algebras all derivations are inner derivations.[23]
Semidirect product (groups)
Consider two Lie groups G and H and Aut H, the automorphism group of H. The latter is the group of isomorphisms of H. If there is a Lie group homomorphism Φ:G → Aut H, then for each g ∈ G there is a Φ(g) ≡ Φg ∈ Aut H with the property Φgg' = ΦgΦg', g,g' ∈ G. Denote with E the set H × G and define multiplication by
-
[math]\displaystyle{ (h, g)(h', g') = (h\phi_g(h'), gg'), \quad g, g' \in G, h, h' \in H. }[/math]
()
Then E is a group with identity (eH, eG) and the inverse is given by (h, g)−1 = (Φg−1(h−1), g−1). Using the expression for the inverse and equation (4) it is seen that H is normal in E. Denote the group with this semidirect product as E = H ⊗S G.
Conversely, if E = H ⊗S G is a given semidirect product expression of the group E, then by definition H is normal in E and Cg ∈ Aut H for each g ∈ G where Cg (h) ≡ ghg−1 and the map Φ:g ↦ Cg is a homomorphism.
Now make use of the Lie correspondence. The maps Φg:H → H, g ∈ G each induce, at the level of Lie algebras, a map Ψg:h → h. This map is computed by
-
[math]\displaystyle{ \Psi_g(G) = \left .\frac{d}{dt}\phi_g(e^{tG})\right|_{t = 0}, \quad G \in \mathfrak g, g \in G. }[/math]
()
For instance, if G and H are both subgroups of a larger group E and Φg = ghg−1, then
-
[math]\displaystyle{ \Psi_g(G) = \left .\frac{d}{dt}ge^{tG}g^{-1}\right|_{t = 0} = gGg^{-1} = \mathrm{Ad}_g(G), }[/math]
()
and one recognizes Ψ as the adjoint action Ad of E on h restricted to G. Now Ψ:G → Aut h [ ⊂ GL(h) if h is finite-dimensional] is a homomorphism,[nb 8] and appealing once more to the Lie correspondence, there is a unique Lie algebra homomorphism ψ:g → Lie(Aut h) = Der h ⊂ gl(h).[nb 9] This map is (formally) given by
-
[math]\displaystyle{ \psi_G = \left .\frac{d}{dt}\Psi_{e^{tG}}\right|_{t=0},\quad G \in \mathfrak g }[/math]
()
for example, if Ψ = Ad, then (formally)
-
[math]\displaystyle{ \psi_G = \left .\frac{d}{dt}\mathrm{Ad}_{e^{tG}}\right|_{t=0} = \left .\frac{d}{dt}e^{\mathrm{ad}_{tG}}\right|_{t=0} = \mathrm{ad}_G, }[/math]
()
where a relationship between Ad and the adjoint action ad rigorously proved in here is used.
Lie algebra
The Lie algebra is, as a vector space, e = h ⊕ g. This is clear since GH generates E and G ∩ H = (eH, eG). The Lie bracket is given by[24]
- [math]\displaystyle{ [H_1 + G_1,H_2 + G_2]_\mathfrak e = [H_1, H_2]_\mathfrak h + \psi_{G_1}(H_2) -\psi_{G_2}(H_1) + [G_1, G_2]_\mathfrak g. }[/math]
To compute the Lie bracket, begin with a surface in E parametrized by s and t. Elements of h in e = h ⊕ g are decorated with a bar, and likewise for g.
- [math]\displaystyle{ \begin{align} e^{e^{t\overline{G}}s\overline{H}e^{-t\overline{G}}} &= e^{t\overline{G}}e^{s\overline{H}}e^{-t\overline{G}}=(1,e^{tG})(e^{sH},1)(1,e^{-tG})\\ &=(\phi_{e^{tG}}(e^{sH}), e^{tG})(1,e^{-tG}) = (\phi_{e^{tG}}(e^{sH})\phi_{e^{tG}}(1),1)\\ &= (\phi_{e^{tG}}(e^{sH}),1) \end{align} }[/math]
One has
- [math]\displaystyle{ \frac{d}{ds} \left. e^{Ad_{e^{t\overline{G}}}s\overline{H}}\right|_{s=0} = Ad_{e^{t\overline{G}}}\overline{H} }[/math]
and
- [math]\displaystyle{ \frac{d}{ds} \left. (\phi_{e^{tG}}(e^{sH}),1)\right|_{s = 0} = (\Psi_{e^{tG}}(H), 0) }[/math]
by 5 and thus
- [math]\displaystyle{ Ad_{e^{t\overline{G}}}\overline{H} = (\Psi_{e^{tG}}(H), 0). }[/math]
Now differentiate this relationship with respect to t and evaluate at t = 0$:
- [math]\displaystyle{ \frac{d}{dt} \left .e^{t\overline{G}}\overline{H}e^{-t\overline{G}}\right|_{t=0} = [\overline{G}, \overline{H}] }[/math]
and
- [math]\displaystyle{ \frac{d}{dt} \left .(\Psi_{e^{tG}}(H), 0)\right|_{t=0} = (\psi_G(H), 0) }[/math]
by 6 and thus
- [math]\displaystyle{ [H_1 + G_1,H_2 + G_2]_\mathfrak e = [H_1, H_2]_\mathfrak h + [G_1, H_2] + [H_1, G_2] + [G_1, G_2]_\mathfrak g = [H_1, H_2]_\mathfrak h + \psi_{G_1}(H_2) -\psi_{G_2}(H_1) + [G_1, G_2]_\mathfrak g. }[/math]
Cohomology
For the present purposes, consideration of a limited portion of the theory Lie algebra cohomology suffices. The definitions are not the most general possible, or even the most common ones, but the objects they refer to are authentic instances of more the general definitions.
2-cocycles
The objects of primary interest are the 2-cocycles on g, defined as bilinear alternating functions,
- [math]\displaystyle{ \phi:\mathfrak g \times \mathfrak g \rightarrow F, }[/math]
that are alternating,
- [math]\displaystyle{ \phi(G_1, G_2) = -\phi(G_2, G_1), }[/math]
and having a property resembling the Jacobi identity called the Jacobi identity for 2-cycles,
- [math]\displaystyle{ \phi(G_1, [G_2, G_3]) + \phi(G_2, [G_3, G_1]) + \phi(G_3, [G_1, G_2]) = 0. }[/math]
The set of all 2-cocycles on g is denoted Z2(g, F).
2-cocycles from 1-cochains
Some 2-cocycles can be obtained from 1-cochains. A 1-cochain on g is simply a linear map,
- [math]\displaystyle{ f:\mathfrak g \rightarrow F }[/math]
The set of all such maps is denoted C1(g, F) and, of course (in at least the finite-dimensional case) C1(g, F) ≅ g*. Using a 1-cochain f, a 2-cocycle δf may be defined by
- [math]\displaystyle{ \delta f(G_1, G_2) = f([G_1, G_2]). }[/math]
The alternating property is immediate and the Jacobi identity for 2-cocycles is (as usual) shown by writing it out and using the definition and properties of the ingredients (here the Jacobi identity on g and the linearity of f). The linear map δ:C1(g, F) → Z2(g, F) is called the coboundary operator (here restricted to C1(g, F)).
The second cohomology group
Denote the image of C1(g, F) of δ by B2(g, F). The quotient
- [math]\displaystyle{ H^2(\mathfrak g, \mathbb F) = Z^2(\mathfrak g, \mathbb F)/B^2(\mathfrak g, \mathbb F) }[/math]
is called the second cohomology group of g. Elements of H2(g, F) are equivalence classes of 2-cocycles and two 2-cocycles φ1 and φ2 are called equivalent cocycles if they differ by a 2-coboundary, i.e. if φ1 = φ2 + δf for some f ∈ C1(g, F). Equivalent 2-cocycles are called cohomologous. The equivalence class of φ ∈ Z2(g, F) is denoted [φ] ∈ H2.
These notions generalize in several directions. For this, see the main articles.
Structure constants
Let B be a Hamel basis for g. Then each G ∈ g has a unique expression as
- [math]\displaystyle{ G = \sum_{\alpha \in A}c_\alpha G_\alpha, \quad c_\alpha \in F, G_\alpha \in B }[/math]
for some indexing set A of suitable size. In this expansion, only finitely many cα are nonzero. In the sequel it is (for simplicity) assumed that the basis is countable, and Latin letters are used for the indices and the indexing set can be taken to be [math]\displaystyle{ \mathbb{N}^* }[/math] = 1, 2, .... One immediately has
- [math]\displaystyle{ [G_i, G_j] = {C_{ij}}^k G_k }[/math]
for the basis elements, where the summation symbol has been rationalized away, the summation convention applies. The placement of the indices in the structure constants (up or down) is immaterial. The following theorem is useful:
Theorem:There is a basis such that the structure constants are antisymmetric in all indices if and only if the Lie algebra is a direct sum of simple compact Lie algebras and u(1) Lie algebras. This is the case if and only if there is a real positive definite metric g on g satisfying the invariance condition
- [math]\displaystyle{ g_{\alpha\beta}{C^\beta}_{\gamma\delta}=-g_{\gamma\beta}{C^\beta}_{\alpha\delta}. }[/math]
in any basis. This last condition is necessary on physical grounds for non-Abelian gauge theories in quantum field theory. Thus one can produce an infinite list of possible gauge theories using the Cartan catalog of simple Lie algebras on their compact form (i.e., sl(n, [math]\displaystyle{ \mathbb{C} }[/math]) → su(n), etc. One such gauge theory is the U(1) × SU(2) × SU(3) gauge theory of the standard model with Lie algebra u(1) ⊕ su(2) ⊕ su(3).[25]
Killing form
The Killing form is a symmetric bilinear form on g defined by
- [math]\displaystyle{ K(G_1, G_2) = \mathrm{trace} (\mathrm{ad}_{G_1}\mathrm{ad}_{G_2}). }[/math]
Here adG is viewed as a matrix operating on the vector space g. The key fact needed is that if g is semisimple, then, by Cartan's criterion, K is non-degenerate. In such a case K may be used to identify g and g∗. If λ ∈ g∗, then there is a ν(λ) = Gλ ∈ g such that
- [math]\displaystyle{ \langle \lambda, G \rangle = K(G_\lambda, G) \quad \forall G \in \mathfrak g. }[/math]
This resembles the Riesz representation theorem and the proof is virtually the same. The Killing form has the property
- [math]\displaystyle{ K([G_1, G_2], G_3) = K(G_1, [G_2, G_3]), }[/math]
which is referred to as associativity. By defining gαβ = K[Gα,Gβ] and expanding the inner brackets in terms of structure constants, one finds that the Killing form satisfies the invariance condition of above.
Loop algebra
A loop group is taken as a group of smooth maps from the unit circle S1 into a Lie group G with the group structure defined by the group structure on G. The Lie algebra of a loop group is then a vector space of mappings from S1 into the Lie algebra g of G. Any subalgebra of such a Lie algebra is referred to as a loop algebra. Attention here is focused on polynomial loop algebras of the form
- [math]\displaystyle{ \{h: S^1 \to \mathfrak g|h(\lambda) = \sum \lambda^n G_n, n \in \mathbb Z, \lambda = e^{i\theta} \in S^1, G_n \in \mathfrak g\}. }[/math]
To see this, consider elements H(λ) near the identity in G for H in the loop group, expressed in a basis {G_k} for g
- [math]\displaystyle{ H(\lambda) = e^{h^k(\lambda)G_k} = e_G + h^k(\lambda)G_k + \ldots , }[/math]
where the hk(λ) are real and small and the implicit sum is over the dimension K of g. Now write
- [math]\displaystyle{ h^k(\lambda) = \sum_{n=-\infty}^\infty \theta^k_{-n}\lambda^n }[/math]
to obtain
- [math]\displaystyle{ e^{h^k(\lambda)G_k} = 1_G + \sum_{n=-\infty}^\infty \theta^k_{-n}\lambda^nG_k + \ldots . }[/math]
Thus the functions
- [math]\displaystyle{ h:S^1 \to \mathfrak g; h(\lambda) = \sum_{n=-\infty}^\infty \sum_{k=1}^K\theta^k_{-n}\lambda^nG_k \equiv \sum_{n=-\infty}^\infty \lambda^nG_n }[/math]
constitute the Lie algebra.
A little thought confirms that these are loops in g as θ goes from 0 to 2π. The operations are the ones defined pointwise by the operations in g. This algebra is isomorphic with the algebra
- [math]\displaystyle{ C[\lambda, \lambda^{-1}] \otimes \mathfrak g, }[/math]
where C[λ, λ−1] is the algebra of Laurent polynomials,
- [math]\displaystyle{ \sum \lambda^k G_k \leftrightarrow \sum \lambda^k \otimes G_k. }[/math]
The Lie bracket is
- [math]\displaystyle{ [P(\lambda) \otimes G_1, Q(\lambda) \otimes G_2] = P(\lambda)Q(\lambda) \otimes [G_1, G_2]. }[/math]
In this latter view the elements can be considered as polynomials with (constant!) coefficients in g. In terms of a basis and structure constants,
- [math]\displaystyle{ [\lambda^m \otimes G_i, \lambda^n \otimes G_j] = {C_{ij}}^k\lambda^{m+n} \otimes G_k. }[/math]
It is also common to have a different notation,
- [math]\displaystyle{ \lambda^m \otimes G_i \cong \lambda^mG_i \leftrightarrow T^m_i(\lambda) \equiv T^m_i, }[/math]
where the omission of λ should be kept in mind to avoid confusion; the elements really are functions S1 → g. The Lie bracket is then
- [math]\displaystyle{ [T^m_i, T^n_j] = {C_{ij}}^kT^{m+n}_k, }[/math]
which is recognizable as one of the commutation relations in an untwisted affine Kac–Moody algebra, to be introduced later, without the central term. With m = n = 0, a subalgebra isomorphic to g is obtained. It generates (as seen by tracing backwards in the definitions) the set of constant maps from S1 into G, which is obviously isomorphic with G when exp is onto (which is the case when G is compact. If G is compact, then a basis (Gk) for g may be chosen such that the Gk are skew-Hermitian. As a consequence,
- [math]\displaystyle{ T_i^{n\dagger} = (\lambda^nG_i)^{\dagger} = -\lambda^{-n}G_i = -T_i^{-n}. }[/math]
Such a representation is called unitary because the representatives
- [math]\displaystyle{ H(\lambda) = e^{\theta_{n}^k T_k^{-n}} \in G }[/math]
are unitary. Here, the minus on the lower index of T is conventional, the summation convention applies, and the λ is (by the definition) buried in the Ts in the right hand side.
Current algebra (physics)
Current algebras arise in quantum field theories as a consequence of global gauge symmetry. Conserved currents occur in classical field theories whenever the Lagrangian respects a continuous symmetry. This is the content of Noether's theorem. Most (perhaps all) modern quantum field theories can be formulated in terms of classical Lagrangians (prior to quantization), so Noether's theorem applies in the quantum case as well. Upon quantization, the conserved currents are promoted to position dependent operators on Hilbert space. These operators are subject to commutation relations, generally forming an infinite-dimensional Lie algebra. A model illustrating this is presented below.
To enhance the flavor of physics, factors of i will appear here and there as opposed to in the mathematical conventions.[nb 3]
Consider a column vector Φ of scalar fields (Φ1, Φ2, ..., ΦN). Let the Lagrangian density be
- [math]\displaystyle{ \mathcal L = \partial_\mu \phi^\dagger\partial^\mu\phi - m^2\phi^\dagger\phi. }[/math]
This Lagrangian is invariant under the transformation[nb 10]
- [math]\displaystyle{ \phi \mapsto e^{-i\sum_{a=1}^r\alpha^aF_a}\phi, }[/math]
where {F1, F1, ..., Fr} are generators of either U(N) or a closed subgroup thereof, satisfying
- [math]\displaystyle{ [F_a, F_b] = i{C_{ab}}^cF_c. }[/math]
Noether's theorem asserts the existence of r conserved currents,
- [math]\displaystyle{ J_a^\mu = -\pi^\mu iF_a\phi, \quad \pi^{k\mu} = \frac{\partial \mathcal L}{\partial (\partial_\mu \phi_k)}, }[/math]
where πk0 ≡ πk is the momentum canonically conjugate to Φk. The reason these currents are said to be conserved is because
- [math]\displaystyle{ \partial_\mu J^\mu_a = 0, }[/math]
and consequently
- [math]\displaystyle{ Q_a(t) = \int J^0_a d^3x = \mathrm{const} \equiv Q_a, }[/math]
the charge associated to the charge density Ja0 is constant in time.[nb 11] This (so far classical) theory is quantized promoting the fields and their conjugates to operators on Hilbert space and by postulating (bosonic quantization) the commutation relations[26][nb 12]
- [math]\displaystyle{ \begin{align}{}[\phi_k(t, x), \pi^l(t, x)] &= i\delta(x-y)\delta_k^l,\\ {}[\phi_k(t, x), \phi_l(t, x)]&= [\pi^k(t, x), \pi^l(t, x)] = 0.\end{align} }[/math]
The currents accordingly become operators[nb 13] They satisfy, using the above postulated relations, the definitions and integration over space, the commutation relations
- [math]\displaystyle{ \begin{align}{}[J_a^0(t, \mathbf x),J_b^0(t, \mathbf y)] &= i\delta(\mathbf x - \mathbf y){C_{ab}}^cJ_c^0(ct, \mathbf x)\\ {}[Q_a, Q_b] &= i{Q_{ab}}^cQ_c\\ {}[Q_a, J_b^\mu(t, \mathbf x)] &= i{C_{ab}}^cJ_c^\mu(t, \mathbf x),\end{align} }[/math]
where the speed of light and the reduced Planck constant have been set to unity. The last commutation relation does not follow from the postulated commutation relations (these are fixed only for πk0, not for πk1, πk2, πk3), except for μ = 0 For μ = 1, 2, 3 the Lorentz transformation behavior is used to deduce the conclusion. The next commutator to consider is
- [math]\displaystyle{ [J_a^0(t, \mathbf x), J_b^i(t, \mathbf y)] = i{C_{ab}}^cJ_c^i(t, \mathbf x)\delta(\mathbf x - \mathbf y) + S_{ab}^{ij}\partial_j\delta(\mathbf x - \mathbf y) + ... . }[/math]
The presence of the delta functions and their derivatives is explained by the requirement of microcausality that implies that the commutator vanishes when x ≠ y. Thus the commutator must be a distribution supported at x = y.[27] The first term is fixed due to the requirement that the equation should, when integrated over X, reduce to the last equation before it. The following terms are the Schwinger terms. They integrate to zero, but it can be shown quite generally[28] that they must be nonzero.
Consider a conserved current
-
[math]\displaystyle{ \partial_0J^0 + \partial_i J^i=0, \quad \langle 0|J^i|0\rangle=0, \quad J^{0\dagger} J^0 = J^0J^{0\dagger} = I. }[/math]
()
with a generic Schwinger term
- [math]\displaystyle{ [J^0(t,\mathbf x),J^i(t,\mathbf y)] = i\delta(\mathbf x - \mathbf y)J^i(t,\mathbf x) + C^i(\mathbf x, \mathbf y). }[/math]
By taking the vacuum expectation value (VEV),
- [math]\displaystyle{ \langle 0|C^i(\mathbf x, \mathbf y)|0\rangle = \langle 0|[J^0(t,\mathbf x),J^i(t,\mathbf y)]|0\rangle, }[/math]
one finds
- [math]\displaystyle{ \begin{align}\langle 0|\frac{\partial C^i(\mathbf x, \mathbf y)}{\partial_{y^i}}|0\rangle &= \langle 0|[J^0(t,\mathbf x),\frac{\partial J^i(t,\mathbf y)}{\partial_{y^i}}]|0\rangle\\ &= -\langle 0|[J^0(t,\mathbf x),\frac{\partial J^0(t,\mathbf y)}{\partial_{t}}]|0\rangle = i\langle 0|[J^0(t,\mathbf x),[J^0(t,\mathbf y),H]]|0\rangle\\ &= -i\langle 0|J^0(t,\mathbf x)HJ^0(t,\mathbf y)+J^0(t,\mathbf x)HJ^0(t,\mathbf x)|0\rangle,\end{align} }[/math]
where S10 and Heisenberg's equation of motion have been used as well as H|0⟩ = 0 and its conjugate.
Multiply this equation by f(x)f(y) and integrate with respect to x and y over all space, using integration by parts, and one finds
- [math]\displaystyle{ -i\int\int d\mathbf x d\mathbf y\langle 0|C^i(\mathbf x, \mathbf y)|0\rangle f(\mathbf x)\frac{\partial f}{\partial y^i}f(\mathbf x) = 2\langle 0|FHF|\rangle, \quad F = \int J^0(\mathbf x)f(\mathbf x). }[/math]
Now insert a complete set of states, |n⟩
- [math]\displaystyle{ \langle 0|FHF|\rangle = \sum_{mn}\langle 0|F|m\rangle\langle m|H|n\rangle\langle n|F|0\rangle=\sum_{mn}\langle 0|F|m\rangle E_n\delta_{mn}\langle n|F|0\rangle ) \sum_{n \ne 0}|\langle 0|F|n\rangle|^2E_n \gt 0 \Rightarrow C^i(\mathbf x, \mathbf y) \ne 0. }[/math]
Here hermiticity of F and the fact that not all matrix elements of F between the vacuum state and the states from a complete set can be zero.
Affine Kac–Moody algebra
Let g be an N-dimensional complex simple Lie algebra with a dedicated suitable normalized basis such that the structure constants are antisymmetric in all indices with commutation relations
- [math]\displaystyle{ [G_i,G_j] = {C_{ij}}^kG_k, \quad 1 \le i, j, N. }[/math]
An untwisted affine Kac–Moody algebra g is obtained by copying the basis for each n ∈ [math]\displaystyle{ \mathbb{Z} }[/math] (regarding the copies as distinct), setting
- [math]\displaystyle{ \overline{\mathfrak g} = FC \oplus FD \oplus \bigoplus_{1 \le i \le \N,m \in \mathbb Z} FG^i_m }[/math]
as a vector space and assigning the commutation relations
- [math]\displaystyle{ \begin{align}{}[G_i^m,G_j^n] &= {C_{ij}}^kG_k^{m+n} + m\delta_{ij}\delta^{m+n,0}C,\\ {}[C,G_i^m] &= 0, \quad 1 \le i, j, N,\quad m,n \in \mathbb Z\\ {}[D, G_i^m] &= mG_i^m\\ {}[D,C] &= 0.\end{align} }[/math]
If C = D = 0, then the subalgebra spanned by the Gmi is obviously identical to the polynomial loop algebra of above.
Witt algebra
The Witt algebra, named after Ernst Witt, is the complexification of the Lie algebra VectS1 of smooth vector fields on the circle S1. In coordinates, such vector fields may be written
- [math]\displaystyle{ X = f(\varphi)\frac{d}{d\varphi}, }[/math]
and the Lie bracket is the Lie bracket of vector fields, on S1 simply given by
- [math]\displaystyle{ [X, Y] = \left[f\frac{d}{d\varphi}, g\frac{d}{d\varphi}\right] = \left(f\frac{dg}{d\varphi} - g\frac{df}{d\varphi}\right)\frac{d}{d\varphi}. }[/math]
The algebra is denoted W = VectS1 + iVectS1. A basis for W is given by the set
- [math]\displaystyle{ \{d_n, n \in \mathbb Z\} = \left\{\left .ie^{in\varphi}\frac{d}{d\varphi} = -z^{n+1}\frac{d}{dz}\right|n \in \mathbb Z \right\}. }[/math]
This basis satisfies
- [math]\displaystyle{ [d_l, d_m] = (l-m)d_{l+m} \equiv {C_{lm}}^nd_n = (l-m)\delta_{l+m}^nd_n,\quad l,m,n \in \mathbb Z. }[/math]
This Lie algebra has a useful central extension, the Virasoro algebra. It has 3-dimensional subalgebras isomorphic with su(1, 1) and sl(2, [math]\displaystyle{ \mathbb{R} }[/math]). For each n ≠ 0, the set {d0, d−n, dn} spans a subalgebra isomorphic to su(1, 1) ≅ sl(2, [math]\displaystyle{ \mathbb{R} }[/math]).
For m, n ∈ {−1, 0, 1} one has
- [math]\displaystyle{ [d_0, d_{-1}] = d_{-1}, \quad [d_0, d_{1}] = -d_{1},\quad [d_1, d_{-1}] = 2d_0. }[/math]
These are the commutation relations of sl(2, [math]\displaystyle{ \mathbb{R} }[/math]) with
- [math]\displaystyle{ d_0 \leftrightarrow H = \left(\begin{smallmatrix} 1 & 0\\ 0 & -1\end{smallmatrix}\right), \quad d_{-1} \leftrightarrow X = \left(\begin{smallmatrix} 0 & 1\\ 0 & 0\end{smallmatrix}\right), \quad d_1 \leftrightarrow Y = \left(\begin{smallmatrix} 0 & 0\\ 1 & 0\end{smallmatrix}\right), \quad H, X, Y \in \mathfrak{sl}(2, \mathbb R). }[/math]
The groups SU(1, 1) and SL(2, [math]\displaystyle{ \mathbb{R} }[/math]) are isomorphic under the map[29]
- [math]\displaystyle{ SU(1,1) = \left(\begin{smallmatrix} 1 & -i\\ 1 & i\end{smallmatrix}\right)SL(2, \mathbb R)\left(\begin{smallmatrix} 1 & -i\\ 1 & i\end{smallmatrix}\right)^{-1}, }[/math]
and the same map holds at the level of Lie algebras due to the properties of the exponential map. A basis for su(1, 1) is given, see classical group, by
- [math]\displaystyle{ U_0 = \left(\begin{smallmatrix} 0 & 1\\ 1 & 0\end{smallmatrix}\right), \quad U_1 = \left(\begin{smallmatrix} 0 & -i\\ i & 0\end{smallmatrix}\right), \quad U_2 = \left(\begin{smallmatrix} i & 0\\ 0 & -i\end{smallmatrix}\right) }[/math]
Now compute
- [math]\displaystyle{ \begin{align}H_{\mathfrak{su}(1,1)} &= \left(\begin{smallmatrix} 1 & -i\\ 1 & i\end{smallmatrix}\right)H\left(\begin{smallmatrix} 1 & -i\\ 1 & i\end{smallmatrix}\right)^{-1} =\left(\begin{smallmatrix} 0 & 1\\ 1 & 0\end{smallmatrix}\right) = U_0,\\ X_{\mathfrak{su}(1,1)} &= \left(\begin{smallmatrix} 1 & -i\\ 1 & i\end{smallmatrix}\right)X\left(\begin{smallmatrix} 1 & -i\\ 1 & i\end{smallmatrix}\right)^{-1} =\frac{1}{2}\left(\begin{smallmatrix} i & -i\\ i & -i\end{smallmatrix}\right) = \frac{1}{2}(U_1+U_2),\\ Y_{\mathfrak{su}(1,1)} &= \left(\begin{smallmatrix} 1 & -i\\ 1 & i\end{smallmatrix}\right)Y\left(\begin{smallmatrix} 1 & -i\\ 1 & i\end{smallmatrix}\right)^{-1} =\frac{1}{2}\left(\begin{smallmatrix} -i & -i\\ i & i\end{smallmatrix}\right) = \frac{1}{2}(U_1-U_2). \end{align} }[/math]
The map preserves brackets and there are thus Lie algebra isomorphisms between the subalgebra of W spanned by {d0, d−1, d1} with real coefficients, sl(2, [math]\displaystyle{ \mathbb{R} }[/math]) and su(1, 1). The same holds for any subalgebra spanned by {d0, d−n, dn}, n ≠ 0, this follows from a simple rescaling of the elements (on either side of the isomorphisms).
Projective representation
If M is a matrix Lie group, then elements X of its Lie algebra m can be given by
- [math]\displaystyle{ X = \frac{d}{dt}\left .(g(t))\right|_{t=0}, }[/math]
where g is a differentiable path in M that goes through the identity element at t = 0. Commutators of elements of the Lie algebra can be computed as[30]
- [math]\displaystyle{ [X_1, X_2] = \left .\frac{d}{dt}\right|_{t = 0}\left .\frac{d}{ds} \right|_{s = 0} e^{tX_1}e^{sX_2}e^{-tX_1}. }[/math]
Likewise, given a group representation U(M), its Lie algebra u(m) is computed by
- [math]\displaystyle{ \begin{align}[] [Y_1, Y_2] &= \left .\frac{d}{dt}\right|_{t = 0}\left .\frac{d}{ds} \right|_{s = 0}U(e^{tX_1})U(e^{sX_2})U(e^{-tX_1})\\ &= \left .\frac{d}{dt}\right|_{t = 0}\left .\frac{d}{ds} \right|_{s = 0}U(e^{tX_1}e^{sX_2}e^{-tX_1})\end{align}, }[/math]
where [math]\displaystyle{ Y_1=\left .\frac{d}{dt}\right|_{t = 0}U(e^{tX_1}) }[/math] and [math]\displaystyle{ Y_2=\left .\frac{d}{ds}\right|_{s = 0}U(e^{sX_2}) }[/math]. Then there is a Lie algebra isomorphism between m and u(m) sending bases to bases, so that u is a faithful representation of m.
If however U(G) is an admissible set of representatives of a projective unitary representation, i.e. a unitary representation up to a phase factor, then the Lie algebra, as computed from the group representation, is not isomorphic to m. For U, the multiplication rule reads
- [math]\displaystyle{ U(g_1)U(g_2) = \omega(g_1, g_2)U(g_1g_2) = e^{i\xi(g_1, g_2)}U(g_1g_2). }[/math]
The function ω,often required to be smooth, satisfies
- [math]\displaystyle{ \begin{align}\omega(g,e)&=\omega(e,g) = 1,\\ \omega(g_1, g_2g_3)\omega(g_2,g_3) &= \omega(g_1,g_2)\omega(g_1g_2,g_3)\\ \omega(g,g^{-1})&=\omega(g^{-1},g).\end{align} }[/math]
It is called a 2-cocycle on M.
From the above equalities, [math]\displaystyle{ (U(g))^{-1}=\frac{1}{\omega(g,g^{-1})}U(g^{-1}) }[/math], so one has
- [math]\displaystyle{ \begin{align}[] [Y_1, Y_2] &= \left .\frac{d}{dt}\right|_{t = 0}\left .\frac{d}{ds} \right|_{s = 0}U(e^{tX_1})U(e^{sX_2})(U(e^{tX_1}))^{-1}\\ &= \left .\frac{d}{dt}\right|_{t = 0}\left .\frac{d}{ds} \right|_{s = 0}\frac{1}{\omega(e^{tX_1},e^{-tX_1})}U(e^{tX_1})U(e^{sX_2})U(e^{-tX_1})\\ &=\left .\frac{d}{dt}\right|_{t = 0}\left .\frac{d}{ds} \right|_{s = 0}\frac{\omega(e^{tX_1},e^{sX_2})\omega(e^{tX_1}e^{sX_2}, e^{-tX_1})}{\omega(e^{tX_1},e^{-tX_1})}U(e^{tX_1}e^{sX_2}e^{-tX_1})\\ &\equiv \left .\frac{d}{dt}\right|_{t = 0}\left .\frac{d}{ds} \right|_{s = 0}\Omega(e^{tX_1},e^{sX_2})U(e^{tX_1}e^{sX_2}e^{-tX_1})\\ &= \left .\frac{d}{dt}\right|_{t = 0}\left .\frac{d}{ds} \right|_{s = 0}U(e^{tX_1}e^{sX_2}e^{-tX_1})+ \left .\frac{d}{dt}\right|_{t = 0}\left .\frac{d}{ds} \right|_{s = 0}\Omega(e^{tX_1},e^{sX_2})I,\end{align} }[/math]
because both Ω and U evaluate to the identity at t = 0. For an explanation of the phase factors ξ, see Wigner's theorem. The commutation relations in m for a basis,
- [math]\displaystyle{ [X_i,X_j] = {C_{ij}^k}X_k }[/math]
become in u
- [math]\displaystyle{ [Y_i,Y_j] = {C_{ij}^k}Y_k + D_{ij}I, }[/math]
so in order for u to be closed under the bracket (and hence have a chance of actually being a Lie algebra) a central charge I must be included.
Relativistic classical string theory
A classical relativistic string traces out a world sheet in spacetime, just like a point particle traces out a world line. This world sheet can locally be parametrized using two parameters σ and τ. Points xμ in spacetime can, in the range of the parametrization, be written xμ = xμ(σ, τ). One uses a capital X to denote points in spacetime actually being on the world sheet of the string. Thus the string parametrization is given by (σ, τ) ↦(X0(σ, τ), X1(σ, τ), X2(σ, τ), X3(σ, τ)). The inverse of the parametrization provides a local coordinate system on the world sheet in the sense of manifolds.
The equations of motion of a classical relativistic string derived in the Lagrangian formalism from the Nambu–Goto action are[31]
- [math]\displaystyle{ \frac{\partial \mathcal P_\mu^\tau}{\partial \tau} + \frac{\partial \mathcal P_\mu^\sigma}{\partial \sigma} = 0, \quad \mathcal P_\mu^\tau = -\frac{T_0}{c}\frac{(\dot X \cdot X')X'_\mu - (X')^2\dot X_\mu}{\sqrt{(\dot X \cdot X')^2 - (\dot X)^2(X')^2}},\quad \mathcal P_\mu^\sigma = -\frac{T_0}{c}\frac{(\dot X \cdot X')X'_\mu - (\dot X)^2 X'_\mu}{\sqrt{(\dot X \cdot X')^2 - (\dot X)^2(X')^2}}. }[/math]
A dot over a quantity denotes differentiation with respect to τ and a prime differentiation with respect to σ. A dot between quantities denotes the relativistic inner product.
These rather formidable equations simplify considerably with a clever choice of parametrization called the light cone gauge. In this gauge, the equations of motion become
- [math]\displaystyle{ \ddot X^\mu - {X^\mu}'' = 0, }[/math]
the ordinary wave equation. The price to be paid is that the light cone gauge imposes constraints,
- [math]\displaystyle{ \dot X^\mu \cdot {X^\mu}' = 0, \quad (\dot X)^2 + (X')^2 = 0, }[/math]
so that one cannot simply take arbitrary solutions of the wave equation to represent the strings. The strings considered here are open strings, i.e. they don't close up on themselves. This means that the Neumann boundary conditions have to be imposed on the endpoints. With this, the general solution of the wave equation (excluding constraints) is given by
- [math]\displaystyle{ X^\mu(\sigma, \tau) = x_0^\mu + 2\alpha'p_0^\mu\tau - i\sqrt{2\alpha'}\sum_{n=1}\left( a_n^{\mu*}e^{in\tau} - a_n^{\mu}e^{-in\tau}\right)\frac{\cos n\sigma}{\sqrt n}, }[/math]
where α' is the slope parameter of the string (related to the string tension). The quantities x0 and p0 are (roughly) string position from the initial condition and string momentum. If all the αμn are zero, the solution represents the motion of a classical point particle.
This is rewritten, first defining
- [math]\displaystyle{ \alpha_0^\mu = \sqrt{2\alpha'}a_ \mu,\quad \alpha_n^\mu = a_n^\mu\sqrt{n}, \quad \alpha_{-n}^\mu = a_n^{\mu*}\sqrt{n}, }[/math]
and then writing
- [math]\displaystyle{ X^\mu(\sigma, \tau) = x_0^\mu + \sqrt{2\alpha'}\alpha_0^\mu \tau + i\sqrt{2\alpha'}\sum_{n\ne 0}\frac{1}{n}\alpha_n^{\mu}e^{-in\tau}\cos n\sigma. }[/math]
In order to satisfy the constraints, one passes to light cone coordinates. For I = 2, 3, ...d, where d is the number of space dimensions, set
- [math]\displaystyle{ \begin{align} X^I(\sigma, \tau) &= x_0^I + \sqrt{2\alpha'}\alpha_0^I \tau + i\sqrt{2\alpha'}\sum_{n \ne 0}\frac{1}{n}\alpha_n^{I}e^{-in\tau}\cos n\sigma,\\ X^+(\sigma, \tau) &= \sqrt{2\alpha'}\alpha_0^+ \tau,\\ X^-(\sigma, \tau) &= x_0^- + \sqrt{2\alpha'}\alpha_0^- \tau + i\sqrt{2\alpha'}\sum_{n \ne 0}\frac{1}{n}\alpha_n^{-}e^{-in\tau}\cos n\sigma. \end{align} }[/math]
Not all αnμ, n ∈ [math]\displaystyle{ \mathbb{Z} }[/math], μ ∈ {+, −, 2, 3, ..., d} are independent. Some are zero (hence missing in the equations above), and the "minus coefficients" satisfy
- [math]\displaystyle{ \sqrt{2\alpha'}\alpha_n^- = \frac{1}{2p^+}\sum_{p \in \mathbb Z}\alpha_{n-p}^I\alpha_p^I. }[/math]
The quantity on the left is given a name,
- [math]\displaystyle{ \sqrt{2\alpha'}\alpha_n^- \equiv \frac{1}{p^+}L_n,\quad L_n = \frac{1}{2}\sum_{p \in \mathbb Z}\alpha_{n-p}^I\alpha_p^I, }[/math]
the transverse Virasoro mode.
When the theory is quantized, the alphas, and hence the Ln become operators.
See also
- Group cohomology
- Group contraction (Inönu–Wigner contraction)
- Group extension
- Lie algebra cohomology
Remarks
- ↑ Otto Schreier (1901 - 1929) was a pioneer in the theory of extension of groups. Along with his rich research papers, his lecture notes were posthumously published (edited by Emanuel Sperner) under the name Einführung in die analytische Geometrie und Algebra (Vol I 1931, Vol II 1935), later in 1951 translated to English in Introduction to Modern Algebra and Matrix Theory. See MacTutor 2015 for further reference.
- ↑ To show that the Jacobi identity holds, one writes everything out, uses the fact that the underlying Lie algebras have a Lie product satisfying the Jacobi identity, and that δ[X, Y] = [δ(X), Y] + [X, δ(Y)].
- ↑ 3.0 3.1 Roughly, the whole Lie algebra is multiplied by i, there is an i occurring in the definition of the structure constants and the exponent in the exponential map (Lie theory) acquires a factor of (minus) i. the main reason for this convention is that physicists like their Lie algebra elements to be Hermitian (as opposed to skew-Hermitian) in order for them to have real eigenvalues and hence be candidates for observables.
- ↑ Miguel Angel Virasoro, born 1940 is an Argentine physicist. The Virasoro algebra, named after him, was first published in (Virasoro 1970)
- ↑ The same effect can be obtained by a change of basis in W.
- ↑ If the 2-cocycle takes its values in the abelian group U(1), i. e. it is a phase factor, which will always be the case in the contezt of Wigner's theorem, then [math]\displaystyle{ \mathbb{C}^* }[/math] may be replaced with U(1) in the construction.
- ↑ Bäuerle, de Kerf & ten Kroode 1997, Chapter 18. The reference states the fact and that it is difficult to show. No further references are given. Expressions on a slightly different form can be found though in (Tuynman Wiegerinck) and (Bargmann 1954).
- ↑ To see this, apply formula (4) to Ψgg', recall that Φ is a homomorphism, and use Φg(eG) = eΨg(G) a couple of times.
- ↑ The fact that the Lie algebra of Aut h) is Der h, the set of all derivations of h (itself being a Lie algebra under the obvious bracket), can be found in Rossmann 2002, p. 51
- ↑ Since U = −iΣαaTa and U† are constant, they may be pulled out of partial derivatives. The U and U† then combine in U†U = I by unitarity.
- ↑ This follows from Gauss law is based on the assumption of a sufficiently rapid fall-off of the fields at infinity.
- ↑ There are alternative routes to quantization, e.g. one postulates the existence of creation and annihilation operators for all particle types with certain exchange symmetries based on which statistics, Bose–Einstein or Fermi–Dirac, the particles obey, in which case the above are derived for scalar bosonic fields using mostly Lorentz invariance and the demand for the unitarity of the S-matrix. In fact, all operators on Hilbert space can be built out of creation and annihilation operators. See e.g. (Weinberg 2002), chapters 2–5.
- ↑ This step is ambiguous, since the classical fields commute whereas the operators don't. Here it is pretended that this problem doesn't exist. In reality, it is never serious as long as one is consistent.
Notes
- ↑ 1.0 1.1 1.2 1.3 Bäuerle, de Kerf & ten Kroode 1997
- ↑ Schottenloher 2008, Introduction
- ↑ Dolan 1995 The Beacon of Kac–Moody Symmetry for Physics. (free access)
- ↑ Green, Schwarz & Witten 1987
- ↑ Schottenloher 2008
- ↑ Schreier 1926
- ↑ Schreier 1925
- ↑ Kac 1967e
- ↑ Moody 1967
- ↑ Bäuerle, de Kerf & ten Kroode 1997, Chapter 19
- ↑ Bäuerle, de Kerf & ten Kroode 1997, Example 18.1.9
- ↑ Bäuerle, de Kerf & ten Kroode 1997, Chapter 18
- ↑ Bäuerle, de Kerf & ten Kroode 1997 Corollary 22.2.9.
- ↑ Kac 1990 Exercise 7.8.
- ↑ Kac 1990
- ↑ Bäuerle & de Kerf 1990
- ↑ Zwiebach 2004, Chapter 12
- ↑ Zwiebach 2004, pp. 219–228
- ↑ Zwiebach 2004, p. 227
- ↑ Bargmann 1954
- ↑ 21.0 21.1 Tuynman & Wiegerinck 1987
- ↑ Rossmann 2002, Section 2.2
- ↑ Humphreys 1972
- ↑ Knapp 2002
- ↑ Weinberg 1996, Appendix A, Ch 15.
- ↑ Greiner & Reinhardt 1996
- ↑ Bäuerle & de Kerf 1990 Section 17.5.
- ↑ Bäuerle & de Kerf 1990, pp. 383–386
- ↑ Rossmann 2002, Section 4.2
- ↑ Hall, Brian (2015). Lie Groups, Lie Algebras, and Representations - An Elementary Introduction (2nd ed.). Switzerland: Springer. p. 57. ISBN 978-3-319-13466-6.
- ↑ Zwiebach 2004 Equation 6.53 (supported by 6.49, 6.50).
References
Books
- Bäuerle, G.G.A; de Kerf, E.A. (1990). Lie algebras. Part 1. Finite and infinite dimensional Lie algebras and their application in physics. Studies in mathematical physics. 1. North-Holland. ISBN 978-0-444-88776-4.
- Bäuerle, G.G.A; de Kerf, E.A.; ten Kroode, A. P. E. (1997). Lie algebras. Part 2. Finite and infinite dimensional Lie algebras and their application in physics. Studies in mathematical physics. 7. North-Holland. ISBN 978-0-444-82836-1. http://www.sciencedirect.com/science/bookseries/09258582.
- Kac–Moody and Virasoro algebras, A reprint Volume for Physicists. Advanced Series in Mathematical Physics. 3. Singapore: World Scientific Publishing. 1988. ISBN 978-9971-50-419-9. https://books.google.com/books?id=Wpk6Q-gFTmwC.
- Goldin, G.A. (2006). Encyclopedia of Mathematical Physics. Current Algebra. ISBN 978-0-12-512666-3.
- Green, M.B.; Schwarz, J.H.; Witten, E. (1987). Superstring theory. l. Cambridge University Press. ISBN 9781107029118.
- Greiner, W.; Reinhardt, J. (1996). Field Quantization. Springer Publishing. ISBN 978-3-540-59179-5. https://archive.org/details/fieldquantizatio0000grei.
- Humphreys, J. E. (1972). Introduction to Lie Algebras and Representation Theory (3rd ed.). Berlin·Heidelberg·New York: Springer-Verlag. ISBN 978-3-540-90053-5. https://archive.org/details/introductiontoli00jame.
- Kac, V.G. (1990). Infinite-dimensional Lie algebras (3rd ed.). Cambridge University Press. ISBN 978-0-521-37215-2.
- Knapp, A. (2002). Lie groups beyond an introduction. Progress in mathematics. 140 (2nd ed.). Boston·Basel·Berlin: Birkhäuser. ISBN 978-0-8176-4259-4.
- Rossmann, Wulf (2002). Lie Groups - An Introduction Through Linear Groups. Oxford Graduate Texts in Mathematics. Oxford Science Publications. ISBN 0-19-859683-9.
- Schottenloher, M. (2008). A Mathematical Introduction to Conformal Field Theory (2nd ed.). Berlin, Heidelberg: Springer-Verlag. ISBN 978-3-540-68625-5.
- Weinberg, S. (2002). The Quantum Theory of Fields. I. Cambridge University Press. ISBN 978-0-521-55001-7. https://archive.org/details/quantumtheoryoff00stev.
- Weinberg, S. (1996). The Quantum Theory of Fields. II. Cambridge University Press. ISBN 978-0-521-55002-4. https://archive.org/details/quantumtheoryoff00stev.
- Zwiebach, B. (2004). A First Course in String Theory. Cambridge University Press. ISBN 0-521-83143-1.
Journals
- Bargmann, V. (1954). "On unitary ray representations of continuous groups". Ann. of Math. 59 (1): 1–46. doi:10.2307/1969831.
- Dolan, L. (1995). "The Beacon of Kac–Moody Symmetry for Physics". Notices of the AMS 42 (12): 1489–1495. ISSN 0002-9920. Bibcode: 1996hep.th....1117D. https://www.ams.org/notices/199512/index.html.
- Kac, V. G. (1967r). "[Simple graded Lie algebras of finite growth]" (in Russian). Funkt. Analis I Ego Prilozh 1 (4): 82–83.
- Kac, V. G. (1967e). "Simple graded Lie algebras of finite growth". Funct. Anal. Appl. 1: 328–329. (English translation)
- Goddard, P.; Olive, D. (1986). "Kac–Moody and Virasoro algebras in relation to quantum physics". Int. J. Mod. Phys. A 1 (2): 303–414. doi:10.1142/S0217751X86000149. Bibcode: 1986IJMPA...1..303G. This can be found in Kac–Moody and Virasoro algebras, A reprint Volume for Physicists
- Moody, R. V. (1967). "Lie algebras associated with generalized Cartan matrices". Bull. Amer. Math. Soc. 73 (2): 217–221. doi:10.1090/S0002-9904-1967-11688-4. (open access)
- Schreier, O. (1926). "Uber die Erweiterung von Gruppen I" (in German). Monatshefte für Mathematik 34 (1): 165–180. doi:10.1007/BF01694897.
- Schreier, O. (1925). "Uber die Erweiterung von Gruppen II" (in German). Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 4 (1): 321–346. doi:10.1007/BF02950735.
- Virasoro, M. A. (1970). "Subsidiary conditions and ghosts in dual-resonance models". Phys. Rev. D 1 (10): 2933–2936. doi:10.1103/PhysRevD.1.2933. Bibcode: 1970PhRvD...1.2933V.
- Tuynman, G.M.; Wiegerinck, W.A.J.J. (1987). "Central extensions and physics". Journal of Geometry and Physics 4 (2): 207–258. doi:10.1016/0393-0440(87)90027-1. Bibcode: 1987JGP.....4..207T.
Web
- MacTutor (2015). "Schreier biography". http://www-history.mcs.st-and.ac.uk/history/Biographies/Schreier.html.
 |