Physics:Schwinger limit

Short description: Energy scale at which vacuum effects become important

A Feynman diagram (box diagram) for photon–photon scattering; one photon scatters from the transient vacuum charge fluctuations of the other.

In quantum electrodynamics (QED), the Schwinger limit is a scale above which the electromagnetic field is expected to become nonlinear. The limit was first derived in one of QED's earliest theoretical successes by Fritz Sauter in 1931 and discussed further by Werner Heisenberg and his student Hans Heinrich Euler. The limit, however, is commonly named in the literature for Julian Schwinger, who derived the leading nonlinear corrections to the fields and calculated the rate of electron–positron pair production in a strong electric field. The limit is typically reported as a maximum electric field or magnetic field before nonlinearity for the vacuum of

[math]\displaystyle{ E_\text{c} = \frac{m_\text{e}^2 c^3}{q_\text{e} \hbar} \simeq 1.32 \times 10^{18} \, \mathrm{V} / \mathrm{m} }[/math]

[math]\displaystyle{ B_\text{c} = \frac{m_\text{e}^2 c^2}{q_\text{e} \hbar} \simeq 4.41 \times 10^{9} \, \mathrm{T} , }[/math]

where m_e is the mass of the electron, c is the speed of light in vacuum, q_e is the elementary charge, and ħ is the reduced Planck constant. These are enormous field strengths. Such an electric field is capable of accelerating a proton from rest to the maximum energy attained by protons at the Large Hadron Collider in only approximately 5 micrometers. The magnetic field is associated with birefringence of the vacuum and is exceeded on magnetars.

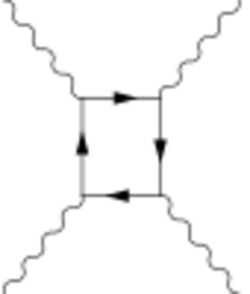
In vacuum, the classical Maxwell's equations are perfectly linear differential equations. This implies – by the superposition principle – that the sum of any two solutions to Maxwell's equations is another solution to Maxwell's equations. For example, two intersecting beams of light should simply add together their electric fields and pass right through each other. Thus Maxwell's equations predict the impossibility of any but trivial elastic photon–photon scattering. In QED, however, non-elastic photon–photon scattering becomes possible when the combined energy is large enough to create virtual electron–positron pairs spontaneously, illustrated by the Feynman diagram in the adjacent figure. This creates nonlinear effects that are approximately described by Euler and Heisenberg's nonlinear variant of Maxwell's equations.

A single plane wave is insufficient to cause nonlinear effects, even in QED. The basic reason for this is that a single plane wave of a given energy may always be viewed in a different reference frame, where it has less energy (the same is the case for a single photon). A single wave or photon does not have a center-of-momentum frame where its energy must be at minimal value. However, two waves or two photons not traveling in the same direction always have a minimum combined energy in their center-of-momentum frame, and it is this energy and the electric field strengths associated with it, which determine particle–antiparticle creation, and associated scattering phenomena.

Photon–photon scattering and other effects of nonlinear optics in vacuum is an active area of experimental research, with current or planned technology beginning to approach the Schwinger limit. It has already been observed through inelastic channels in SLAC Experiment 144. However, the direct effects in elastic scattering have not been observed. As of 2012, the best constraint on the elastic photon–photon scattering cross section belonged to PVLAS, which reported an upper limit far above the level predicted by the Standard Model.

Proposals were made to measure elastic light-by-light scattering using the strong electromagnetic fields of the hadrons collided at the LHC. In 2019, the ATLAS experiment at the LHC announced the first definitive observation of photon–photon scattering, observed in lead ion collisions that produced fields as large as 10²⁵ V/m, well in excess of the Schwinger limit. Observation of a cross section larger or smaller than that predicted by the Standard Model could signify new physics such as axions, the search of which is the primary goal of PVLAS and several similar experiments. ATLAS observed more events than expected, potentially evidence that the cross section is larger than predicted by the Standard Model, but the excess is not yet statistically significant.

The planned, funded ELI–Ultra High Field Facility, which will study light at the intensity frontier, is likely to remain well below the Schwinger limit although it may still be possible to observe some nonlinear optical effects. The Station of Extreme Light (SEL) is another laser facility under construction which should be powerful enough to observe the effect. Such an experiment, in which ultra-intense light causes pair production, has been described in the popular media as creating a "hernia" in spacetime.

See also

• Julian Schwinger
• Schwinger effect
• Sokolov–Ternov effect
• Vacuum polarization