Replication (statistics)
In engineering, science, and statistics, replication is the process of repeating a study or experiment under the same or similar conditions to support the original claim, which crucial to confirm the accuracy of results as well as for identifying and correcting the flaws in the original experiment.[1] ASTM, in standard E1847, defines replication as "... the repetition of the set of all the treatment combinations to be compared in an experiment. Each of the repetitions is called a replicate."
For a full factorial design, replicates are multiple experimental runs with the same factor levels. You can replicate combinations of factor levels, groups of factor level combinations, or even entire designs. For instance, consider a scenario with three factors, each having two levels, and an experiment that tests every possible combination of these levels (a full factorial design). One complete replication of this design would comprise 8 runs (2^3). The design can be executed once or with several replicates.[2]
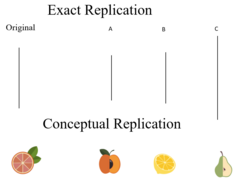
There are two main types of replication in statistics. First, there is a type called “exact replication” (also called "direct replication"), which involves repeating the study as closely as possible to the original to see whether the original results can be precisely reproduced.[3] For instance, repeating a study on the effect of a specific diet on weight loss using the same diet plan and measurement methods. The second type of replication is called “conceptual replication.” This involves testing the same theory as the original study but with different conditions.[3] For example, Testing the same diet's effect on blood sugar levels instead of weight loss, using different measurement methods.
Both exact (direct) replications and conceptual replications are important. Direct replications help confirm the accuracy of the findings within the conditions that were initially tested. On the hand conceptual replications examine the validity of the theory, behind those findings and explore different conditions under which those findings remain true. In essence conceptual replication provides insights, into how generalizable the findings are.[4]
The difference between replicates and repeats
Replication is not the same as repeated measurements of the same item. Both repeat and replicate measurements involve multiple observations taken at the same levels of experimental factors. However, repeat measurements are collected during a single experimental session, while replicate measurements are gathered across different experimental sessions.[2] Replication in statistics evaluates the consistency of experiment results across different trials to ensure external validity, while repetition measures precision and internal consistency within the same or similar experiments.[5]
Replicates Example: Testing a new drug's effect on blood pressure in separate groups on different days.
Repeats Example: Measuring blood pressure multiple times in one group during a single session.
Statistical methods in replication
In replication studies within the field of statistics, several key methods and concepts are employed to assess the reliability of research findings. Here are some of the main statistical methods and concepts used in replication:
P-Values: The p-value is a measure of the probability that the observed data would occur by chance if the null hypothesis were true. In replication studies p-values help us determine whether the findings can be consistently replicated. A low p-value in a replication study indicates that the results are not likely due to random chance.[6] For example, if a study found a statistically significant effect of a test condition on an outcome, and the replication find statistically significant effects as well, this suggests that the original finding is likely reproducible.
Confidence Intervals: Confidence intervals provide a range of values within which the true effect size is likely to fall. In replication studies, comparing the confidence intervals of the original study and the replication can indicate whether the results are consistent.[6] For example, if the original study reports a treatment effect with a 95% confidence interval of [5, 10], and the replication study finds a similar effect with a confidence interval of [6, 11], this overlap indicates consistent findings across both studies.
Example
As an example, consider a continuous process which produces items. Batches of items are then processed or treated. Finally, tests or measurements are conducted. Several options might be available to obtain ten test values. Some possibilities are:
- One finished and treated item might be measured repeatedly to obtain ten test results. Only one item was measured so there is no replication. The repeated measurements help identify observational error.
- Ten finished and treated items might be taken from a batch and each measured once. This is not full replication because the ten samples are not random and not representative of the continuous nor batch processing.
- Five items are taken from the continuous process based on sound statistical sampling. These are processed in a batch and tested twice each. This includes replication of initial samples but does not allow for batch-to-batch variation in processing. The repeated tests on each provide some measure and control of testing error.
- Five items are taken from the continuous process based on sound statistical sampling. These are processed in five different batches and tested twice each. This plan includes proper replication of initial samples and also includes batch-to-batch variation. The repeated tests on each provide some measure and control of testing error.
- For proper sampling, a process or batch of products should be in reasonable statistical control; inherent random variation is present but variation due to assignable (special) causes is not. Evaluation or testing of a single item does not allow for item-to-item variation and may not represent the batch or process. Replication is needed to account for this variation among items and treatments.
Each option would call for different data analysis methods and yield different conclusions.
See also
- Degrees of freedom (statistics)
- Design of experiments
- Pseudoreplication
- Sample size
- Statistical ensemble
- Statistical process control
- Test method
References
- ↑ Killeen, Peter R. (2008), "Replication Statistics", Best Practices in Quantitative Methods (2455 Teller Road, Thousand Oaks California 91320 United States of America: SAGE Publications, Inc.): pp. 102–124, doi:10.4135/9781412995627.d10, ISBN 978-1-4129-4065-8, https://methods.sagepub.com/book/best-practices-in-quantitative-methods/d10.xml, retrieved 2023-12-11
- ↑ 2.0 2.1 "Replicates and repeats in designed experiments" (in en-US). https://support.minitab.com/en-us/minitab/21/help-and-how-to/statistical-modeling/doe/supporting-topics/basics/replicates-and-repeats-in-designed-experiments/#:~:text=Repeat%20and%20replicate%20measurements%20are,experimental%20runs,%20which%20are%20often.
- ↑ 3.0 3.1 "The Replication Crisis in Psychology" (in en). https://nobaproject.com/modules/the-replication-crisis-in-psychology.
- ↑ Hudson, Robert (2023-08-01). "Explicating Exact versus Conceptual Replication" (in en). Erkenntnis 88 (6): 2493–2514. doi:10.1007/s10670-021-00464-z. ISSN 1572-8420. PMID 37388139. PMC 10300171. https://doi.org/10.1007/s10670-021-00464-z.
- ↑ Ruiz, Nicole (2023-09-07). "Repetition vs Replication: Key Differences" (in en-US). https://sixsigmadsi.com/repetition-vs-replication-key-differences/.
- ↑ 6.0 6.1 "How are confidence intervals useful in understanding replication?" (in en). 2016-12-08. https://scientificallysound.org/2016/12/08/how-are-confidence-intervals-useful-in-understanding-replication/.
Bibliography
- ASTM E122-07 Standard Practice for Calculating Sample Size to Estimate, With Specified Precision, the Average for a Characteristic of a Lot or Process
- "Engineering Statistics Handbook", NIST/SEMATEK
- Pyzdek, T, "Quality Engineering Handbook", 2003, ISBN 0-8247-4614-7.
- Godfrey, A. B., "Juran's Quality Handbook", 1999, ISBN 9780070340039.
 |
