Physics:X-ray fluorescence

File:TEDxDelft 3D scanning of the Staalmeesters.webm


X-ray fluorescence (XRF) is a powerful non-destructive analytical technique. In simple terms, it works by illuminating a sample with high-energy X-rays, causing the atoms within to become excited and emit their own unique, characteristic X-rays—a process similar to how a blacklight makes certain colors fluoresce. By measuring the energy and intensity of these emitted "secondary" X-rays, scientists can identify which elements are present in the sample and in what quantities. More technically, XRF is the emission of characteristic "secondary" (or fluorescent) X-rays from a material that has been excited by being bombarded with high-energy X-rays or gamma rays.
The phenomenon is widely used for elemental analysis and chemical analysis, particularly in the investigation of metals, glass, ceramics and building materials, and for research in geochemistry, forensic science, archaeology and art objects[1] such as paintings.[2][3]
Underlying physics

When materials are exposed to short-wavelength X-rays or to gamma rays, ionization of their component atoms may take place. Ionization consists of the ejection of one or more electrons from the atom, and may occur if the atom is exposed to radiation with an energy greater than its ionization energy. X-rays and gamma rays can be energetic enough to expel tightly held electrons from the inner orbitals of the atom.
The removal of an electron in this way makes the electronic structure of the atom unstable, and electrons in higher orbitals "fall" into the lower orbital to fill the hole left behind. In falling, energy is released in the form of a photon, the energy of which is equal to the energy difference of the two orbitals involved. Thus, the material emits radiation, which has energy characteristic of the atoms present. The term fluorescence is applied to phenomena in which the absorption of radiation of a specific energy results in the re-emission of radiation of a different energy (generally lower).
Characteristic radiation
Each element has electronic orbitals of characteristic energy. Following removal of an inner electron by an energetic photon provided by a primary radiation source, an electron from an outer shell drops into its place. There are a limited number of ways in which this can happen, as shown in Figure 1. The main transitions are given names: an L→K transition is traditionally called Kα, an M→K transition is called Kβ, an M→L transition is called Lα, and so on. Each of these transitions yields a fluorescent photon with a characteristic energy equal to the difference in energy of the initial and final orbital. The wavelength of this fluorescent radiation can be calculated from Planck's law:
The fluorescent radiation can be analysed either by sorting the energies of the photons (energy-dispersive analysis) or by separating the wavelengths of the radiation (wavelength-dispersive analysis). Once sorted, the intensity of each characteristic radiation is directly related to the amount of each element in the material. This is the basis of a powerful technique in analytical chemistry. The typical form of the sharp fluorescent spectral lines obtained in the wavelength-dispersive method is illustrated in Figure 2 (see Moseley's law).


Primary radiation sources
In order to excite the atoms, a source of radiation is required, with sufficient energy to expel tightly held inner electrons. Conventional X-ray generators, based on electron bombardment of a heavy metal (i.e. tungsten or rhodium) target are most commonly used, because their output can readily be "tuned" for the application, and because higher power can be deployed relative to other techniques. X-ray generators in the range 20–60 kV are used, which allow excitation of a broad range of atoms. The continuous spectrum consists of "bremsstrahlung" radiation: radiation produced when high-energy electrons passing through the tube are progressively decelerated by the material of the tube anode (the "target"). A typical tube output spectrum is shown in Figure 3.
For portable XRF spectrometers, copper target is usually bombarded with high energy electrons, that are produced either by impact laser or by pyroelectric crystals.[4][5]
Alternatively, gamma ray sources, based on radioactive isotopes (such as 109Cd, 57Co, 55Fe, 238Pu and 241Am) can be used without the need for an elaborate power supply, allowing for easier use in small, portable instruments.[6]
When the energy source is a synchrotron or the X-rays are focused by an optic like a polycapillary, the X-ray beam can be very small and very intense. As a result, atomic information on the sub-micrometer scale can be obtained.
Dispersion
In energy-dispersive analysis, the fluorescent X-rays emitted by the material sample are directed into a solid-state detector which produces a "continuous" distribution of pulses, the voltages of which are proportional to the incoming photon energies. This signal is processed by a multichannel analyzer (MCA) which produces an accumulating digital spectrum that can be processed to obtain analytical data.
In wavelength-dispersive analysis, the fluorescent X-rays emitted by the sample are directed into a diffraction grating-based monochromator. The diffraction grating used is usually a single crystal. By varying the angle of incidence and take-off on the crystal, a small X-ray wavelength range can be selected. The wavelength obtained is given by Bragg's law:
where d is the spacing of atomic layers parallel to the crystal surface.
Detection

In energy-dispersive analysis, dispersion and detection are a single operation, as already mentioned above. Proportional counters or various types of solid-state detectors (PIN diode, Si(Li), Ge(Li), silicon drift detector SDD) are used. They all share the same detection principle: An incoming X-ray photon ionizes a large number of detector atoms with the amount of charge produced being proportional to the energy of the incoming photon. The charge is then collected and the process repeats itself for the next photon. Detector speed is obviously critical, as all charge carriers measured have to come from the same photon to measure the photon energy correctly (peak length discrimination is used to eliminate events that seem to have been produced by two X-ray photons arriving almost simultaneously). The spectrum is then built up by dividing the energy spectrum into discrete bins and counting the number of pulses registered within each energy bin. EDXRF detector types vary in resolution, speed and the means of cooling (a low number of free charge carriers is critical in the solid state detectors): proportional counters with resolutions of several hundred eV cover the low end of the performance spectrum, followed by PIN diode detectors, while the Si(Li), Ge(Li) and SDDs occupy the high end of the performance scale.
In wavelength-dispersive analysis, the single-wavelength radiation produced by the monochromator is passed into a chamber containing a gas that is ionized by the X-ray photons. A central electrode is charged at (typically) +1700 V with respect to the conducting chamber walls, and each photon triggers a pulse-like cascade of current across this field. The signal is amplified and transformed into an accumulating digital count. These counts are then processed to obtain analytical data.
X-ray intensity
The fluorescence process is inefficient, and the secondary radiation is much weaker than the primary beam. Furthermore, the secondary radiation from lighter elements is of relatively low energy (long wavelength) and has low penetrating power, and is severely attenuated if the beam passes through air for any distance. Because of this, for high-performance analysis, the path from tube to sample to detector is maintained under vacuum (around 10 Pa residual pressure). This means in practice that most of the working parts of the instrument have to be located in a large vacuum chamber. The problems of maintaining moving parts in vacuum, and of rapidly introducing and withdrawing the sample without losing vacuum, pose major challenges for the design of the instrument. For less demanding applications, or when the sample is damaged by a vacuum (e.g. a volatile sample), a helium-swept X-ray chamber can be substituted, with some loss of low-Z (Z = atomic number) intensities.
Chemical analysis
The use of a primary X-ray beam to excite fluorescent radiation from the sample was first proposed by Glocker and Schreiber in 1928.[7] Today, the method is used as a non-destructive analytical technique, and as a process control tool in many extractive and processing industries. In principle, the lightest element that can be analysed is beryllium (Z = 4), but due to instrumental limitations and low X-ray yields for the light elements, it is often difficult to quantify elements lighter than sodium (Z = 11), unless background corrections and very comprehensive inter-element corrections are made.

Energy dispersive spectrometry
In energy-dispersive spectrometers (EDX or EDS), the detector allows the determination of the energy of the photon when it is detected. Detectors historically have been based on silicon semiconductors, in the form of lithium-drifted silicon crystals, or high-purity silicon wafers.
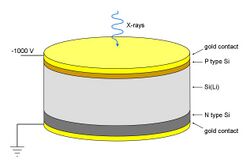
Si(Li) detectors
These consist essentially of a 3–5 mm thick silicon junction type p-i-n diode (same as PIN diode) with a bias of −1000 V across it. The lithium-drifted centre part forms the non-conducting i-layer, where Li compensates the residual acceptors which would otherwise make the layer p-type. When an X-ray photon passes through, it causes a swarm of electron-hole pairs to form, and this causes a voltage pulse. To obtain sufficiently low conductivity, the detector must be maintained at low temperature, and liquid-nitrogen cooling must be used for the best resolution. With some loss of resolution, the much more convenient Peltier cooling can be employed.[8]
Wafer detectors
More recently, high-purity silicon wafers with low conductivity have become routinely available. Cooled by the Peltier effect, this provides a cheap and convenient detector, although the liquid nitrogen cooled Si(Li) detector still has the best resolution (i.e. ability to distinguish different photon energies).
Amplifiers
The pulses generated by the detector are processed by pulse-shaping amplifiers. It takes time for the amplifier to shape the pulse for optimum resolution, and there is therefore a trade-off between resolution and count-rate: long processing time for good resolution results in "pulse pile-up" in which the pulses from successive photons overlap. Multi-photon events are, however, typically more drawn out in time (photons did not arrive exactly at the same time) than single photon events and pulse-length discrimination can thus be used to filter most of these out. Even so, a small number of pile-up peaks will remain and pile-up correction should be built into the software in applications that require trace analysis. To make the most efficient use of the detector, the tube current should be reduced to keep multi-photon events (before discrimination) at a reasonable level, e.g. 5–20%.
Therefore, managing this trade-off between speed and accuracy is a fundamental consideration in modern XRF instrument design, especially for high-throughput industrial applications.
Processing
Considerable computer power is dedicated to correcting for pulse-pile up and for extraction of data from poorly resolved spectra. These elaborate correction processes tend to be based on empirical relationships that may change with time, so that continuous vigilance is required in order to obtain chemical data of adequate precision.
Digital pulse processors are widely used in high performance nuclear instrumentation. They are able to effectively reduce pile-up and base line shifts, allowing for easier processing. A low pass filter is integrated, improving the signal to noise ratio. The digital pulse processor requires a significant amount of energy to run, but it provides precise results.
Usage
Energy-dispersive X-ray (EDX) spectrometers are different from wavelength dispersive X-ray (WDX) spectrometers in that they are smaller, simpler in design and have fewer engineered parts; however, the accuracy and resolution of EDX spectrometers are lower than for WDX. EDX spectrometers can also use miniature X-ray tubes or gamma sources, which makes them cheaper and allows miniaturization and portability. This type of instrument is commonly used for portable quality control screening applications, such as testing toys for lead (Pb) content, sorting scrap metals, and measuring the lead content of residential paint. On the other hand, the low resolution and problems with low count rate and long dead-time makes them inferior for high-precision analysis. They are, however, very effective for high-speed, multi-elemental analysis. Field portable XRF analysers currently on the market weigh less than 2 kg, and have limits of detection on the order of 2 parts per million of lead (Pb) in pure sand. Using a scanning electron microscope and using EDX, studies have been broadened to organic based samples such as biological samples and polymers.
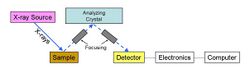

Wavelength dispersive spectrometry
In wavelength dispersive spectrometers (WDX or WDS), the emitted photons are separated by diffraction on a single crystal before being detected. Although wavelength dispersive spectrometers are occasionally used to scan a wide range of wavelengths, producing a spectrum plot as in EDS, they are usually set up to make measurements only at the wavelength of the emission lines of the elements of interest. This is achieved in two different ways:
- "Simultaneous" spectrometers have a number of "channels" dedicated to analysis of a single element, each consisting of a fixed-geometry crystal monochromator, a detector, and processing electronics. This allows a number of elements to be measured simultaneously, and in the case of high-powered instruments, complete high-precision analyses can be obtained in under 30 s. Another advantage of this arrangement is that the fixed-geometry monochromators have no continuously moving parts, and so are very reliable. Reliability is important in production environments where instruments are expected to work without interruption for months at a time. Disadvantages of simultaneous spectrometers include relatively high cost for complex analyses, since each channel used is expensive. The number of elements that can be measured is limited to 15–20, because of space limitations on the number of monochromators that can be crowded around the fluorescing sample. The need to accommodate multiple monochromators means that a rather open arrangement around the sample is required, leading to relatively long tube-sample-crystal distances, which leads to lower detected intensities and more scattering. The instrument is inflexible, because if a new element is to be measured, a new measurement channel has to be bought and installed.
- "Sequential" spectrometers have a single variable-geometry monochromator (but usually with an arrangement for selecting from a choice of crystals), a single detector assembly (but usually with more than one detector arranged in tandem), and a single electronic pack. The instrument is programmed to move through a sequence of wavelengths, in each case selecting the appropriate X-ray tube power, the appropriate crystal, and the appropriate detector arrangement. The length of the measurement program is essentially unlimited, so this arrangement is very flexible. Because there is only one monochromator, the tube-sample-crystal distances can be kept very short, resulting in minimal loss of detected intensity. The obvious disadvantage is relatively long analysis time, particularly when many elements are being analysed, not only because the elements are measured in sequence, but also because a certain amount of time is taken in readjusting the monochromator geometry between measurements. Furthermore, the frenzied activity of the monochromator during an analysis program is a challenge for mechanical reliability. However, modern sequential instruments can achieve reliability almost as good as that of simultaneous instruments, even in continuous-usage applications.
Sample preparation
In order to keep the geometry of the tube-sample-detector assembly constant, the sample is normally prepared as a flat disc, typically of diameter 20–50 mm. This is located at a standardized, small distance from the tube window. Because the X-ray intensity follows an inverse-square law, the tolerances for this placement and for the flatness of the surface must be very tight in order to maintain a repeatable X-ray flux. Ways of obtaining sample discs vary: metals may be machined to shape, minerals may be finely ground and pressed into a tablet, and glasses may be cast to the required shape. A further reason for obtaining a flat and representative sample surface is that the secondary X-rays from lighter elements often only emit from the top few micrometers of the sample. In order to further reduce the effect of surface irregularities, the sample is usually spun at 5–20 rpm. It is necessary to ensure that the sample is sufficiently thick to absorb the entire primary beam. For higher-Z materials, a few millimeters thickness is adequate, but for a light-element matrix such as coal, a thickness of 30–40 mm is needed.
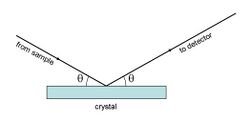
Monochromators
The common feature of monochromators is the maintenance of a symmetrical geometry between the sample, the crystal and the detector. In this geometry the Bragg diffraction condition is obtained.
The X-ray emission lines are very narrow (see figure 2), so the angles must be defined with considerable precision. This is achieved in two ways:
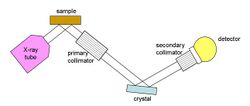
Flat crystal with Söller collimators
A Söller collimator is a stack of parallel metal plates, spaced a few tenths of a millimeter apart. To improve angular resolution, one must lengthen the collimator, and/or reduce the plate spacing. This arrangement has the advantage of simplicity and relatively low cost, but the collimators reduce intensity and increase scattering, and reduce the area of sample and crystal that can be "seen". The simplicity of the geometry is especially useful for variable-geometry monochromators.

Curved crystal with slits
The Rowland circle geometry ensures that the slits are both in focus, but in order for the Bragg condition to be met at all points, the crystal must first be bent to a radius of 2R (where R is the radius of the Rowland circle), then ground to a radius of R. This arrangement allows higher intensities (typically 8-fold) with higher resolution (typically 4-fold) and lower background. However, the mechanics of keeping Rowland circle geometry in a variable-angle monochromator is extremely difficult. In the case of fixed-angle monochromators (for use in simultaneous spectrometers), crystals bent to a logarithmic spiral shape give the best focusing performance. The manufacture of curved crystals to acceptable tolerances increases their price considerably.
Crystal materials
An intuitive understanding of X-ray diffraction can be obtained from the Bragg model of diffraction. In this model, a given reflection is associated with a set of evenly spaced sheets running through the crystal, usually passing through the centers of the atoms of the crystal lattice. The orientation of a particular set of sheets is identified by its three Miller indices (h, k, l), and let their spacing be noted by d. William Lawrence Bragg proposed a model in which the incoming X-rays are scattered specularly (mirror-like) from each plane; from that assumption, X-rays scattered from adjacent planes will combine constructively (constructive interference) when the angle θ between the plane and the X-ray results in a path-length difference that is an integer multiple n of the X-ray wavelength λ.(Fig.7)
- High diffraction intensity
- High dispersion
- Narrow diffracted peak width
- High peak-to-background
- Absence of interfering elements
- Low thermal coefficient of expansion
- Stability in air and on exposure to X-rays
- Ready availability
- Low cost
Crystals with simple structures tend to give the best diffraction performance. Crystals containing heavy atoms can diffract well, but also fluoresce more in the higher energy region, causing interference. Crystals that are water-soluble, volatile or organic tend to give poor stability.
Commonly used crystal materials include LiF (lithium fluoride), ADP (ammonium dihydrogen phosphate), Ge (germanium), Si (silicon), graphite, InSb (indium antimonide), PE (tetrakis-(hydroxymethyl)-methane, also known as pentaerythritol), KAP (potassium hydrogen phthalate), RbAP (rubidium hydrogen phthalate) and TlAP (thallium(I) hydrogen phthalate). In addition, there is an increasing use of "layered synthetic microstructures" (LSMs), which are "sandwich" structured materials comprising successive thick layers of low atomic number matrix, and monatomic layers of a heavy element. These can in principle be custom-manufactured to diffract any desired long wavelength, and are used extensively for elements in the range Li to Mg.
In scientific methods that use X-ray/neutron or electron diffraction the before mentioned planes of a diffraction can be doubled to display higher order reflections. The given planes, resulting from Miller indices, can be calculated for a single crystal. The resulting values for h, k and l are then called Laue indices. So a single crystal can be variable in the way, that many reflection configurations of that crystal can be used to reflect different energy ranges. The germanium (Ge111) crystal, for example, can also be used as a Ge333, Ge444 and more.
For that reason, the corresponding indices used for a particular experimental setup always get noted behind the crystal material (e.g. Ge111, Ge444).
The Ge222 configuration is forbidden due to diffraction rules stating that all allowed reflections must be with all odd or all even Miller indices that, combined, result in , where is the order of reflection.
| material | plane | d (nm) | min λ (nm) | max λ (nm) | intensity | thermal expansion | durability |
|---|---|---|---|---|---|---|---|
| LiF | 200 | 0.2014 | 0.053 | 0.379 | +++++ | +++ | +++ |
| LiF | 220 | 0.1424 | 0.037 | 0.268 | +++ | ++ | +++ |
| LiF | 420 | 0.0901 | 0.024 | 0.169 | ++ | ++ | +++ |
| ADP | 101 | 0.5320 | 0.139 | 1.000 | + | ++ | ++ |
| Ge | 111 | 0.3266 | 0.085 | 0.614 | +++ | + | +++ |
| Ge | 222 | 0,1633 | forbidden | forbidden | +++ | + | +++ |
| Ge | 333 | 0,1088 | 0,17839 | 0,21752 | +++ | + | +++ |
| Ge | 444 | 0,0816 | 0,13625 | 0,16314 | +++ | + | +++ |
| Ge | 310 | 0,1789 | forbidden | forbidden | +++ | + | +++ |
| Ge | 620 | 0,0894 | 0,14673 | 0,17839 | +++ | + | +++ |
| Graphite | 001 | 0.3354 | 0.088 | 0.630 | ++++ | + | +++ |
| InSb | 111 | 0.3740 | 0.098 | 0.703 | ++++ | + | +++ |
| PE | 002 | 0.4371 | 0.114 | 0.821 | +++ | +++++ | + |
| KAP | 1010 | 1.325 | 0.346 | 2.490 | ++ | ++ | ++ |
| RbAP | 1010 | 1.305 | 0.341 | 2.453 | ++ | ++ | ++ |
| Si | 111 | 0.3135 | 0.082 | 0.589 | ++ | + | +++ |
| TlAP | 1010 | 1.295 | 0.338 | 2.434 | +++ | ++ | ++ |
| YB66 | 400 | 0.586 | |||||
| 6 nm LSM | - | 6.00 | 1.566 | 11.276 | +++ | + | ++ |
Elemental analysis lines
The spectral lines used for elemental analysis of chemicals are selected on the basis of intensity, accessibility by the instrument, and lack of line overlaps. Typical lines used, and their wavelengths and energies, are as follows:
| element | line | wavelength (nm) | Energy (eV) | element | line | wavelength (nm) | Energy (eV) | element | line | wavelength (nm) | Energy (eV) | element | line | wavelength (nm) | Energy (eV) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Li | Kα | 22.8 | 54.38 | Ni | Kα1 | 0.1658 | 7477.94 | I | Lα1 | 0.3149 | 3937.26 | Pt | Lα1 | 0.1313 | 9442.82 | |||
| Be | Kα | 11.4 | 108.76 | Cu | Kα1 | 0.1541 | 8045.70 | Xe | Lα1 | 0.3016 | 4110.88 | Au | Lα1 | 0.1276 | 9716.63 | |||
| B | Kα | 6.76 | 183.41 | Zn | Kα1 | 0.1435 | 8640.01 | Cs | Lα1 | 0.2892 | 4287.14 | Hg | Lα1 | 0.1241 | 9990.67 | |||
| C | Kα | 4.47 | 277.37 | Ga | Kα1 | 0.1340 | 9252.55 | Ba | Lα1 | 0.2776 | 4466.29 | Tl | Lα1 | 0.1207 | 10272.10 | |||
| N | Kα | 3.16 | 392.36 | Ge | Kα1 | 0.1254 | 9887.10 | La | Lα1 | 0.2666 | 4650.57 | Pb | Lα1 | 0.1175 | 10551.85 | |||
| O | Kα | 2.362 | 524.91 | As | Kα1 | 0.1176 | 10542.87 | Ce | Lα1 | 0.2562 | 4839.35 | Bi | Lα1 | 0.1144 | 10837.78 | |||
| F | Kα1,2 | 1.832 | 676.77 | Se | Kα1 | 0.1105 | 11220.29 | Pr | Lα1 | 0.2463 | 5033.87 | Po | Lα1 | 0.1114 | 11129.64 | |||
| Ne | Kα1,2 | 1.461 | 848.63 | Br | Kα1 | 0.1040 | 11921.56 | Nd | Lα1 | 0.2370 | 5231.40 | At | Lα1 | 0.1085 | 11427.12 | |||
| Na | Kα1,2 | 1.191 | 1041.01 | Kr | Kα1 | 0.09801 | 12650.16 | Pm | Lα1 | 0.2282 | 5433.14 | Rn | Lα1 | 0.1057 | 11729.82 | |||
| Mg | Kα1,2 | 0.989 | 1253.63 | Rb | Kα1 | 0.09256 | 13395.01 | Sm | Lα1 | 0.2200 | 5635.65 | Fr | Lα1 | 0.1031 | 12025.63 | |||
| Al | Kα1,2 | 0.834 | 1486.62 | Sr | Kα1 | 0.08753 | 14164.77 | Eu | Lα1 | 0.2121 | 5845.55 | Ra | Lα1 | 0.1005 | 12336.74 | |||
| Si | Kα1,2 | 0.7126 | 1739.88 | Y | Kα1 | 0.08288 | 14959.48 | Gd | Lα1 | 0.2047 | 6056.87 | Ac | Lα1 | 0.0980 | 12651.45 | |||
| P | Kα1,2 | 0.6158 | 2013.38 | Zr | Kα1 | 0.07859 | 15776.08 | Tb | Lα1 | 0.1977 | 6271.33 | Th | Lα1 | 0.0956 | 12969.06 | |||
| S | Kα1,2 | 0.5373 | 2307.54 | Nb | Kα1 | 0.07462 | 16615.41 | Dy | Lα1 | 0.1909 | 6494.72 | Pa | Lα1 | 0.0933 | 13288.77 | |||
| Cl | Kα1,2 | 0.4729 | 2621.78 | Mo | Kα1 | 0.07094 | 17477.33 | Ho | Lα1 | 0.1845 | 6720.01 | U | Lα1 | 0.0911 | 13609.68 | |||
| Ar | Kα1,2 | 0.4193 | 2956.93 | Tc | Kα1 | 0.06751 | 18365.31 | Er | Lα1 | 0.1784 | 6949.79 | Np | Lα1 | 0.0888 | 13962.18 | |||
| K | Kα1,2 | 0.3742 | 3313.31 | Ru | Kα1 | 0.06433 | 19273.15 | Tm | Lα1 | 0.1727 | 7179.17 | Pu | Lα1 | 0.0868 | 14283.89 | |||
| Ca | Kα1,2 | 0.3359 | 3691.10 | Rh | Kα1 | 0.06136 | 20206.03 | Yb | Lα1 | 0.1672 | 7415.32 | Am | Lα1 | 0.0847 | 14638.04 | |||
| Sc | Kα1,2 | 0.3032 | 4089.19 | Pd | Kα1 | 0.05859 | 21161.32 | Lu | Lα1 | 0.1620 | 7653.35 | Cm | Lα1 | 0.0828 | 14973.94 | |||
| Ti | Kα1,2 | 0.2749 | 4510.16 | Ag | Kα1 | 0.05599 | 22143.99 | Hf | Lα1 | 0.1570 | 7897.08 | Bk | Lα1 | 0.0809 | 15325.61 | |||
| V | Kα1 | 0.2504 | 4951.45 | Cd | Kα1 | 0.05357 | 23144.33 | Ta | Lα1 | 0.1522 | 8146.14 | Cf | Lα1 | 0.0791 | 15674.36 | |||
| Cr | Kα1 | 0.2290 | 5414.16 | In | Lα1 | 0.3772 | 3286.96 | W | Lα1 | 0.1476 | 8400.01 | Es | Lα1 | 0.0773 | 16039.35 | |||
| Mn | Kα1 | 0.2102 | 5898.39 | Sn | Lα1 | 0.3600 | 3444.01 | Re | Lα1 | 0.1433 | 8652.07 | Fm | Lα1 | 0.0756 | 16400.03 | |||
| Fe | Kα1 | 0.1936 | 6404.14 | Sb | Lα1 | 0.3439 | 3605.24 | Os | Lα1 | 0.1391 | 8913.31 | Md | Lα1 | 0.0740 | 16754.62 | |||
| Co | Kα1 | 0.1789 | 6930.36 | Te | Lα1 | 0.3289 | 3769.66 | Ir | Lα1 | 0.1351 | 9177.22 | No | Lα1 | 0.0724 | 17124.89 |
Other lines are often used, depending on the type of sample and equipment available.
Structural analysis lines
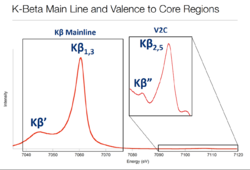
X-ray diffraction (XRD) is still the most used method for structural analysis of crystallographic compounds. Yet, with increasing detail on the relation of -line spectra and the surrounding chemical environment of the ionized metal atom, measurements of the so-called valence-to-core (VtC) energy region become increasingly viable.
Scientists noted that after ionization of 3d-transition metal atom, the -line intensities and energies shift with oxidation state of the metal and with the species of ligand(s). Spin states in a compound tend to affect this kind of measurement.[9]
This means, that by intense study of these spectral lines, one can obtain several crucial pieces of information from a sample. Especially, if there are references that have been studied in detail and can be used to make out differences. The information collected from this kind of measurement include:
- Oxidation state of the central metal atom in a compound (shifts of -mainline in low-spin complexes)
- Spin states of transition metal complexes (general shape of - and -mainlines)
- Identity and orientation of ligands bonded to the central metal atom (from the satellite)[10]
These measurements are mostly done at synchrotron facilities, although a number of so-called "in-lab"-spectrometers[11] have been developed and used for pre-beamtime (time at a synchrotron) measurements.[12][13]
Detectors
Detectors used for wavelength dispersive spectrometry need to have high pulse processing speeds in order to cope with the very high photon count rates that can be obtained. In addition, they need sufficient energy resolution to allow filtering-out of background noise and spurious photons from the primary beam or from crystal fluorescence. There are four common types of detector:
- gas flow proportional counters
- sealed gas detectors
- scintillation counters
- semiconductor detectors
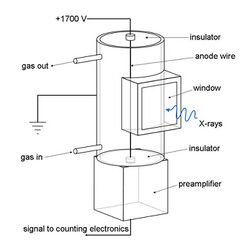
Gas flow proportional counters are used mainly for detection of longer wavelengths. Gas flows through it continuously. Where there are multiple detectors, the gas is passed through them in series, then led to waste. The gas is usually 90% argon, 10% methane ("P10"), although the argon may be replaced with neon or helium where very long wavelengths (over 5 nm) are to be detected. The argon is ionized by incoming X-ray photons, and the electric field multiplies this charge into a measurable pulse. The methane suppresses the formation of fluorescent photons caused by recombination of the argon ions with stray electrons. The anode wire is typically tungsten or nichrome of 20–60 μm diameter. Since the pulse strength obtained is essentially proportional to the ratio of the detector chamber diameter to the wire diameter, a fine wire is needed, but it must also be strong enough to be maintained under tension so that it remains precisely straight and concentric with the detector. The window needs to be conductive, thin enough to transmit the X-rays effectively, but thick and strong enough to minimize diffusion of the detector gas into the high vacuum of the monochromator chamber. Materials often used are beryllium metal, aluminised PET film and aluminised polypropylene. Ultra-thin windows (down to 1 μm) for use with low-penetration long wavelengths are very expensive. The pulses are sorted electronically by "pulse height selection" in order to isolate those pulses deriving from the secondary X-ray photons being counted.
Sealed gas detectors are similar to the gas flow proportional counter, except that the gas does not flow through it. The gas is usually krypton or xenon at a few atmospheres pressure. They are applied usually to wavelengths in the 0.15–0.6 nm range. They are applicable in principle to longer wavelengths, but are limited by the problem of manufacturing a thin window capable of withstanding the high pressure difference.
Scintillation counters consist of a scintillating crystal (typically of sodium iodide doped with thallium) attached to a photomultiplier. The crystal produces a group of scintillations for each photon absorbed, the number being proportional to the photon energy. This translates into a pulse from the photomultiplier of voltage proportional to the photon energy. The crystal must be protected with a relatively thick aluminium/beryllium foil window, which limits the use of the detector to wavelengths below 0.25 nm. Scintillation counters are often connected in series with a gas flow proportional counter: the latter is provided with an outlet window opposite the inlet, to which the scintillation counter is attached. This arrangement is particularly used in sequential spectrometers.
Semiconductor detectors can be used in theory, and their applications are increasing as their technology improves, but historically their use for WDX has been restricted by their slow response (see EDX).

Extracting analytical results
At first sight, the translation of X-ray photon count-rates into elemental concentrations would appear to be straightforward: WDX separates the X-ray lines efficiently, and the rate of generation of secondary photons is proportional to the element concentration. However, the number of photons leaving the sample is also affected by the physical properties of the sample: so-called "matrix effects". These fall broadly into three categories:
- X-ray absorption
- X-ray enhancement
- sample macroscopic effects
All elements absorb X-rays to some extent. Each element has a characteristic absorption spectrum which consists of a "saw-tooth" succession of fringes, each step-change of which has wavelength close to an emission line of the element. Absorption attenuates the secondary X-rays leaving the sample. For example, the mass absorption coefficient of silicon at the wavelength of the aluminium Kα line is 50 m2/kg, whereas that of iron is 377 m2/kg. This means that fluorescent X-rays generated by a given concentration of aluminium in a matrix of iron are absorbed about seven times more (that is 377/50) compared with the fluorescent X-rays generated by the same concentration of aluminium, but in a silicon matrix. That would lead to about one seventh of the count rate, once the X-rays are detected. Mass absorption coefficients are well known and can be calculated. However, to calculate the absorption for a multi-element sample, the composition must be known. For analysis of an unknown sample, an iterative procedure is therefore used. To derive the mass absorption accurately, data for the concentration of elements not measured by XRF may be needed, and various strategies are employed to estimate these. As an example, in cement analysis, the concentration of oxygen (which is not measured) is calculated by assuming that all other elements are present as standard oxides.
Enhancement occurs where the secondary X-rays emitted by a heavier element are sufficiently energetic to stimulate additional secondary emission from a lighter element. This phenomenon can also be modelled, and corrections can be made provided that the full matrix composition can be deduced.
Sample macroscopic effects consist of effects of inhomogeneities of the sample, and unrepresentative conditions at its surface. Samples are ideally homogeneous and isotropic, but they often deviate from this ideal. Mixtures of multiple crystalline components in mineral powders can result in absorption effects that deviate from those calculable from theory. When a powder is pressed into a tablet, the finer minerals concentrate at the surface. Spherical grains tend to migrate to the surface more than do angular grains. In machined metals, the softer components of an alloy tend to smear across the surface. Considerable care and ingenuity are required to minimize these effects. Because they are artifacts of the method of sample preparation, these effects can not be compensated by theoretical corrections, and must be "calibrated in". This means that the calibration materials and the unknowns must be compositionally and mechanically similar, and a given calibration is applicable only to a limited range of materials. Glasses most closely approach the ideal of homogeneity and isotropy, and for accurate work, minerals are usually prepared by dissolving them in a borate glass, and casting them into a flat disc or "bead". Prepared in this form, a virtually universal calibration is applicable.
Further corrections that are often employed include background correction and line overlap correction. The background signal in an XRF spectrum derives primarily from scattering of primary beam photons by the sample surface. Scattering varies with the sample mass absorption, being greatest when mean atomic number is low. When measuring trace amounts of an element, or when measuring on a variable light matrix, background correction becomes necessary. This is really only feasible on a sequential spectrometer. Line overlap is a common problem, bearing in mind that the spectrum of a complex mineral can contain several hundred measurable lines. Sometimes it can be overcome by measuring a less-intense, but overlap-free line, but in certain instances a correction is inevitable. For instance, the Kα is the only usable line for measuring sodium, and it overlaps the zinc Lβ (L2-M4) line. Thus zinc, if present, must be analyzed in order to properly correct the sodium value.
Other spectroscopic methods using the same principle
It is also possible to create a characteristic secondary X-ray emission using other incident radiation to excite the sample:
- electron beam: electron microprobe;
- ion beam: particle induced X-ray emission (PIXE).
When radiated by an X-ray beam, the sample also emits other radiations that can be used for analysis:
- electrons ejected by the photoelectric effect: X-ray photoelectron spectroscopy (XPS), also called electron spectroscopy for chemical analysis (ESCA)
The de-excitation also ejects Auger electrons, but Auger electron spectroscopy (AES) normally uses an electron beam as the probe.
Confocal microscopy X-ray fluorescence imaging is a newer technique that allows control over depth, in addition to horizontal and vertical aiming, for example, when analysing buried layers in a painting.[14]
Instrument qualification
A 2022 review[15] addresses the application of portable instrumentation from quality assurance/quality control perspectives. It provides a guide to the development of a set of Standard Operating Procedures if regulatory compliance guidelines are not available.
See also
- Physics:Emission spectroscopy
- Chemistry:List of materials analysis methods
- Physics:Micro-X-ray fluorescence
- Physics:Mössbauer effect – Resonant and recoil-free emission and absorption of gamma radiation by atomic nuclei, resonant fluorescence of gamma rays
- Physics:X-ray fluorescence holography
Notes
- ↑ [NEW_REF_1 - Replace old ref 1 with current review on XRF applications]
- ↑ Janssens, K. (2020). "Recent developments in spectroscopic imaging techniques for historical painting analysis". Applied Physics A 126 (2): 1-15.
- ↑ Mantler, M. (2022). X-ray fluorescence in art and archaeology. Springer.
- ↑ Smith, A. (2021). "Advances in portable XRF technology for field analysis". Journal of Analytical Chemistry 76 (4): 512-525.
- ↑ Johnson, M. (2022). "Recent developments in miniaturized X-ray sources". pp. 234-241.
- ↑ Chen, H. (2023). "Radioisotope sources in modern analytical instrumentation: safety and applications review". Radiation Physics and Chemistry 204: 110-125.
- ↑ Glocker, R., and Schreiber, H., Annalen der Physik., 85, (1928), p. 1089
- ↑ Thompson, A. (2020). "Modern X-ray detector technologies: a comparative review". Journal of Synchrotron Radiation 27: 1234-1247.
- ↑ Bergmann, U. (2021). "X-ray spectroscopy for chemical and energy science: the case of metalloproteins". Nature Reviews Chemistry 5: 842-858.
- ↑ Lee, N. (2020). "Probing ligand effects in iron complexes using high-resolution X-ray spectroscopy". Inorganic Chemistry 59 (15): 10416-10426.
- ↑ Smith, P. (2022). "Bench-top X-ray spectrometers for chemical state analysis". Analytical Chemistry Reviews 94 (3): 112-125.
- ↑ Jones, R. (2021). "Laboratory-based X-ray emission spectroscopy: a new tool for studying electronic structure". Journal of Chemical Physics 155: 150901.
- ↑ Chen, W. (2023). "Advances in tabletop X-ray spectroscopy for materials characterization". Materials Today Advances 18: 100-115.
- ↑ L. Vincze (2005). "Confocal X-ray Fluorescence Imaging and XRF Tomography for Three-Dimensional Trace Element Microanalysis". Microscopy and Microanalysis 11: 682. doi:10.1017/S1431927605503167.
- ↑ Anderson, K. (2022). "Quality assurance and quality control for portable X-ray fluorescence spectrometry: current practices and new directions". Spectrochimica Acta Part B 188: 106-120.
References
- Beckhoff, B., Kanngießer, B., Langhoff, N., Wedell, R., Wolff, H., Handbook of Practical X-Ray Fluorescence Analysis, Springer, 2006, ISBN 3-540-28603-9
- Bertin, E. P., Principles and Practice of X-ray Spectrometric Analysis, Kluwer Academic / Plenum Publishers, ISBN 0-306-30809-6
- Buhrke, V. E., Jenkins, R., Smith, D. K., A Practical Guide for the Preparation of Specimens for XRF and XRD Analysis, Wiley, 1998, ISBN 0-471-19458-1
- Jenkins, R., X-ray Fluorescence Spectrometry, Wiley, ISBN 0-471-29942-1
- Jenkins, R., De Vries, J. L., Practical X-ray Spectrometry, Springer-Verlag, 1973, ISBN 0-387-91029-8
- Jenkins, R., R.W. Gould, R. W., Gedcke, D., Quantitative X-ray Spectrometry, Marcel Dekker, ISBN 0-8247-9554-7
- Penner-Hahn, James E. (2013). "Chapter 2. Technologies for Detecting Metals in Single Cells. Section 4, Intrinsic X-Ray Fluorescence". in Banci, Lucia. Metallomics and the Cell. Metal Ions in Life Sciences. 12. Springer. pp. 15–40. doi:10.1007/978-94-007-5561-1_2. ISBN 978-94-007-5560-4.electronic-book ISBN 978-94-007-5561-1 ISSN 1559-0836electronic-ISSN 1868-0402
- Van Grieken, R. E., Markowicz, A. A., Handbook of X-Ray Spectrometry 2nd ed.; Marcel Dekker Inc.: New York, 2002; Vol. 29; ISBN 0-8247-0600-5
External links
 |
