600-cell
- REDIRECT Template:Infobox 4-polytope
This page is a redirect. The following categories are used to track and monitor this redirect:
|
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,5}. It is also known as the C600, hexacosichoron[1] and hexacosihedroid.[2] It is also called a tetraplex (abbreviated from "tetrahedral complex") and a polytetrahedron, being bounded by tetrahedral cells.
The 600-cell's boundary is composed of 600 tetrahedral cells with 20 meeting at each vertex.[lower-alpha 1] Together they form 1200 triangular faces, 720 edges, and 120 vertices. It is the 4-dimensional analogue of the icosahedron, since it has five tetrahedra meeting at every edge, just as the icosahedron has five triangles meeting at every vertex.[lower-alpha 2] Its dual polytope is the 120-cell.
Geometry
The 600-cell is the fifth in the sequence of 6 convex regular 4-polytopes (in order of size and complexity).[lower-alpha 3] It can be deconstructed into twenty-five overlapping instances of its immediate predecessor the 24-cell,[4] as the 24-cell can be deconstructed into three overlapping instances of its predecessor the tesseract (8-cell), and the 8-cell can be deconstructed into two overlapping instances of its predecessor the 16-cell.[5]
The reverse procedure to construct each of these from an instance of its predecessor preserves the radius of the predecessor, but generally produces a successor with a smaller edge length.[lower-alpha 4] The 24-cell's edge length equals its radius, but the 600-cell's edge length is ~0.618 times its radius. The 600-cell's radius and edge length are in the golden ratio.
Coordinates
Unit radius Cartesian coordinates
The vertices of a 600-cell of unit radius centered at the origin of 4-space, with edges of length 1/φ ≈ 0.618 (where φ = 1 + √5/2 ≈ 1.618 is the golden ratio), can be given[6] as follows:
8 vertices obtained from
- (0, 0, 0, ±1)
by permuting coordinates, and 16 vertices of the form:
- (±1/2, ±1/2, ±1/2, ±1/2)
The remaining 96 vertices are obtained by taking even permutations of
- (±φ/2, ±1/2, ±φ−1/2, 0)
Note that the first 8 are the vertices of a 16-cell, the second 16 are the vertices of a tesseract, and those 24 vertices together are the vertices of a 24-cell. The remaining 96 vertices are the vertices of a snub 24-cell, which can be found by partitioning each of the 96 edges of another 24-cell (dual to the first) in the golden ratio in a consistent manner.[7]
When interpreted as quaternions,[lower-alpha 5] these are the unit icosians.
In the 24-cell, there are squares, hexagons and triangles that lie on great circles (in central planes through four or six vertices).[lower-alpha 6] In the 600-cell there are twenty-five overlapping inscribed 24-cells, with each vertex and square shared by five 24-cells, and each hexagon or triangle shared by two 24-cells.[lower-alpha 8] In each 24-cell there are three disjoint 16-cells, so in the 600-cell there are 75 overlapping inscribed 16-cells.[lower-alpha 9] Each 16-cell constitutes a distinct orthonormal basis for the choice of a coordinate reference frame.
The 60 axes and 75 16-cells of the 600-cell constitute a geometric configuration, which in the language of configurations is written as 605754 to indicate that each axis belongs to 5 16-cells, and each 16-cell contains 4 axes.[8] Each axis is orthogonal to exactly 15 others, and these are just its companions in the 5 16-cells in which it occurs.
Hopf spherical coordinates
In the 600-cell there are also great circle pentagons and decagons (in central planes through ten vertices).[lower-alpha 14]
Only the decagon edges are visible elements of the 600-cell (because they are the edges of the 600-cell). The edges of the other great circle polygons are interior chords of the 600-cell, which are not shown in any of the 600-cell renderings in this article (except where shown as dashed lines).
By symmetry, an equal number of polygons of each kind pass through each vertex; so it is possible to account for all 120 vertices as the intersection of a set of central polygons of only one kind: decagons, hexagons, pentagons, squares, or triangles. For example, the 120 vertices can be seen as the vertices of 15 pairs of completely orthogonal[lower-alpha 16] squares which do not share any vertices, or as 100 dual pairs of non-orthogonal hexagons between which all axis pairs are orthogonal, or as 144 non-orthogonal pentagons six of which intersect at each vertex. This latter pentagonal symmetry of the 600-cell is captured by the set of Hopf coordinates[lower-alpha 19] (𝜉i, 𝜂, 𝜉j) given as:
- ({<10}𝜋/5, {≤5}𝜋/10, {<10}𝜋/5)
where {<10} is the permutation of the ten digits (0 1 2 3 4 5 6 7 8 9) and {≤5} is the permutation of the six digits (0 1 2 3 4 5). The 𝜉i and 𝜉j coordinates range over the 10 vertices of great circle decagons; even and odd digits label the vertices of the two great circle pentagons inscribed in each decagon.[lower-alpha 20]
Structure
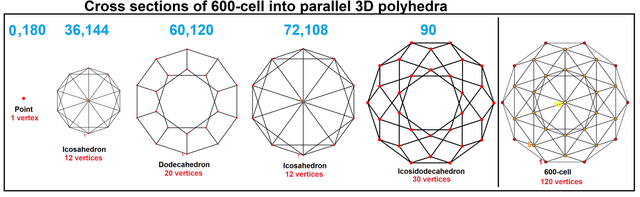
Polyhedral sections
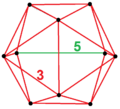
The mutual distances of the vertices, measured in degrees of arc on the circumscribed hypersphere, only have the values 36° = 𝜋/5, 60° = 𝜋/3, 72° = 2𝜋/5, 90° = 𝜋/2, 108° = 3𝜋/5, 120° = 2𝜋/3, 144° = 4𝜋/5, and 180° = 𝜋. Departing from an arbitrary vertex V one has at 36° and 144° the 12 vertices of an icosahedron,[lower-alpha 1] at 60° and 120° the 20 vertices of a dodecahedron, at 72° and 108° the 12 vertices of a larger icosahedron, at 90° the 30 vertices of an icosidodecahedron, and finally at 180° the antipodal vertex of V.[11][12][13] These can be seen in the H3 Coxeter plane projections with overlapping vertices colored.[14]
These polyhedral sections are solids in the sense that they are 3-dimensional, but of course all of their vertices lie on the surface of the 600-cell (they are hollow, not solid). Each polyhedron lies in Euclidean 4-dimensional space as a parallel cross section through the 600-cell (a hyperplane). In the curved 3-dimensional space of the 600-cell's boundary surface envelope, the polyhedron surrounds the vertex V the way it surrounds its own center. But its own center is in the interior of the 600-cell, not on its surface. V is not actually at the center of the polyhedron, because it is displaced outward from that hyperplane in the fourth dimension, to the surface of the 600-cell. Thus V is the apex of a 4-pyramid based on the polyhedron.
Golden chords
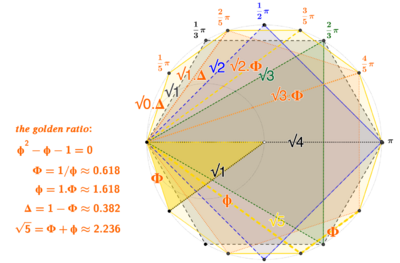
The 120 vertices are distributed[15] at eight different chord lengths from each other. These edges and chords of the 600-cell are simply the edges and chords of its five great circle polygons.[16] In ascending order of length, they are √0.𝚫, √1, √1.𝚫, √2, √2.𝚽, √3, √3.𝚽, and √4.[lower-alpha 24]
Notice that the four hypercubic chords of the 24-cell (√1, √2, √3, √4)[lower-alpha 6] alternate with the four new chords of the 600-cell's additional great circles, the decagons and pentagons. The new golden chord lengths are necessarily square roots of fractions, but very special fractions related to the golden ratio[lower-alpha 21] including the two golden sections of √5, as shown in the diagram.[lower-alpha 22]
Boundary envelopes

The 600-cell rounds out the 24-cell by adding 96 more vertices between the 24-cell's existing 24 vertices,[lower-alpha 26] in effect adding twenty-four more overlapping 24-cells inscribed in the 600-cell.[lower-alpha 9] The new surface thus formed is a tessellation of smaller, more numerous cells[lower-alpha 27] and faces: tetrahedra of edge length 1/φ ≈ 0.618 instead of octahedra of edge length 1. It encloses the √1 edges of the 24-cells, which become invisible interior chords in the 600-cell, like the √2 and √3 chords.

Since the tetrahedra are made of shorter triangle edges than the octahedra (by a factor of 1/φ, the inverse golden ratio), the 600-cell does not have unit edge-length in a unit-radius coordinate system the way the 24-cell and the tesseract do; unlike those two, the 600-cell is not radially equilateral. Like them it is radially triangular in a special way, but one in which golden triangles rather than equilateral triangles meet at the center.[lower-alpha 23]
The boundary envelope of 600 small tetrahedral cells wraps around the twenty-five envelopes of 24 octahedral cells (adding some 4-dimensional space in places between these curved 3-dimensional envelopes). The shape of those interstices must be an octahedral 4-pyramid of some kind, but in the 600-cell it is not regular.[lower-alpha 29]
Geodesics
The vertex chords of the 600-cell are arranged in geodesic great circle polygons of five kinds: decagons, hexagons, pentagons, squares, and triangles.[19]

The √0.𝚫 = 𝚽 edges form 72 flat regular central decagons, 6 of which cross at each vertex.[lower-alpha 1] Just as the icosidodecahedron can be partitioned into 6 central decagons (60 edges = 6 × 10), the 600-cell can be partitioned into 72 decagons (720 edges = 72 × 10). The 720 √0.𝚫 edges divide the surface into 1200 triangular faces and 600 tetrahedral cells: a 600-cell. The 720 edges occur in 360 parallel pairs, √3.𝚽 apart. As in the decagon and the icosidodecahedron, the edges occur in golden triangles[lower-alpha 28] which meet at the center of the polytope.[lower-alpha 23] The 72 great decagons can be divided into 6 sets of 12 non-intersecting Clifford parallel geodesics,[lower-alpha 33] such that only one decagonal great circle in each set passes through each vertex, and the 12 decagons in each set reach all 120 vertices.[21]
The √1 chords form 200 central hexagons (25 sets of 16, with each hexagon in two sets),[lower-alpha 7] 10 of which cross at each vertex[lower-alpha 34] (4 from each of five 24-cells that meet at the vertex, with each hexagon in two of those 24-cells).[lower-alpha 12] Each set of 16 hexagons consists of the 96 edges and 24 vertices of one of the 25 overlapping inscribed 24-cells. The √1 chords join vertices which are two √0.𝚫 edges apart. Each √1 chord is the long diameter of a face-bonded pair of tetrahedral cells (a triangular bipyramid), and passes through the center of the shared face. As there are 1200 faces, there are 1200 √1 chords, in 600 parallel pairs, √3 apart. The hexagonal planes are non-orthogonal (60 degrees apart) but they occur as 100 dual pairs in which all 3 axes of one hexagon are orthogonal to all 3 axes of its dual.[22] The 200 great hexagons can be divided into 10 sets of 20 non-intersecting Clifford parallel geodesics, such that only one hexagonal great circle in each set passes through each vertex, and the 20 hexagons in each set reach all 120 vertices.[23]
The √1.𝚫 chords form 144 central pentagons, 6 of which cross at each vertex.[lower-alpha 14] The √1.𝚫 chords run vertex-to-every-second-vertex in the same planes as the 72 decagons: two pentagons are inscribed in each decagon. The √1.𝚫 chords join vertices which are two √0.𝚫 edges apart on a geodesic great circle. The 720 √1.𝚫 chords occur in 360 parallel pairs, √2.𝚽 = φ apart.
The √2 chords form 450 central squares, 15 of which cross at each vertex (3 from each of the five 24-cells that meet at the vertex). The √2 chords join vertices which are three √0.𝚫 edges apart (and two √1 chords apart). There are 600 √2 chords, in 300 parallel pairs, √2 apart. The 450 great squares (225 completely orthogonal[lower-alpha 16] pairs) can be divided into 15 sets of 30 non-intersecting Clifford parallel geodesics, such that only one square great circle in each set passes through each vertex, and the 30 squares (15 completely orthogonal pairs) in each set reach all 120 vertices.[24]
The √2.𝚽 = φ chords form the legs of 720 central isosceles triangles (72 sets of 10 inscribed in each decagon), 6 of which cross at each vertex. The third edge (base) of each isosceles triangle is of length √3.𝚽. The √2.𝚽 chords run vertex-to-every-third-vertex in the same planes as the 72 decagons, joining vertices which are three √0.𝚫 edges apart on a geodesic great circle. There are 720 distinct √2.𝚽 chords, in 360 parallel pairs, √1.𝚫 apart.
The √3 chords form 400 equilateral central triangles (25 sets of 32, with each triangle in two sets), 10 of which cross at each vertex (4 from each of five 24-cells, with each triangle in two of the 24-cells). Each set of 32 triangles consists of the 96 √3 chords and 24 vertices of one of the 25 overlapping inscribed 24-cells. The √3 chords run vertex-to-every-second-vertex in the same planes as the 200 hexagons: two triangles are inscribed in each hexagon. The √3 chords join vertices which are four √0.𝚫 edges apart (and two √1 chords apart on a geodesic great circle). Each √3 chord is the long diameter of two cubic cells in the same 24-cell.[lower-alpha 35] There are 1200 √3 chords, in 600 parallel pairs, √1 apart.
The √3.𝚽 chords (the diagonals of the pentagons) form the legs of 720 central isosceles triangles (144 sets of 5 inscribed in each pentagon), 6 of which cross at each vertex. The third edge (base) of each isosceles triangle is an edge of the pentagon of length √1.𝚫, so these are golden triangles.[lower-alpha 28] The √3.𝚽 chords run vertex-to-every-fourth-vertex in the same planes as the 72 decagons, joining vertices which are four √0.𝚫 edges apart on a geodesic great circle. There are 720 distinct √3.𝚽 chords, in 360 parallel pairs, √0.𝚫 apart.
The √4 chords occur as 60 long diameters (75 sets of 4 orthogonal axes with each set comprising a 16-cell), the 120 long radii of the 600-cell. The √4 chords join opposite vertices which are five √0.𝚫 edges apart on a geodesic great circle. There are 25 distinct but overlapping sets of 12 diameters, each comprising one of the 25 inscribed 24-cells.[lower-alpha 13] There are 75 distinct but overlapping sets of 4 orthogonal diameters, each comprising one of the 75 inscribed 16-cells.
The sum of the squared lengths[lower-alpha 36] of all these distinct chords of the 600-cell is 14,400 = 1202.[lower-alpha 37] These are all the central polygons through vertices, but the 600-cell does have one noteworthy great circle that does not pass through any vertices (a 0-gon).[lower-alpha 41] Moreover, in 4-space there are geodesics on the 3-sphere which do not lie in central planes at all. There are geodesic shortest paths between two 600-cell vertices that are helical rather than simply circular; they correspond to isoclinic (diagonal) rotations rather than simple rotations.[lower-alpha 42]
All the geodesic polygons enumerated above lie in central planes of just three kinds, each characterized by a rotation angle: decagon planes (𝜋/5 apart), hexagon planes (𝜋/3 apart, also in the 25 inscribed 24-cells), and square planes (𝜋/2 apart, also in the 75 inscribed 16-cells and the 24-cells). These central planes of the 600-cell can be divided into 4 orthogonal central hyperplanes (3-spaces) each forming an icosidodecahedron. There are 450 great squares 90 degrees apart; 200 great hexagons 60 degrees apart; and 72 great decagons 36 degrees apart.[lower-alpha 47] Each great square plane is completely orthogonal[lower-alpha 16] to another great square plane. Each great hexagon plane is completely orthogonal to a plane which intersects only two vertices (one √4 long diameter): a great digon plane.[lower-alpha 48] Each great decagon plane is completely orthogonal to a plane which intersects no vertices: a great 0-gon plane.[lower-alpha 39]
Fibrations of great circle polygons
Each set of similar great circle polygons (squares or hexagons or decagons) can be divided into bundles of non-intersecting Clifford parallel great circles (of 30 squares or 20 hexagons or 12 decagons).[lower-alpha 33] Each fiber bundle of Clifford parallel great circles[lower-alpha 43] is a discrete Hopf fibration which fills the 600-cell, visiting all 120 vertices just once.[29] Each discrete Hopf fibration has its 3-dimensional base which is a distinct polyhedron that acts as a map or scale model of the fibration.[lower-alpha 49] The great circle polygons in each bundle spiral around each other, delineating helical rings of face-bonded cells which nest into each other, pass through each other without intersecting in any cells and exactly fill the 600-cell with their disjoint cell sets. The different fiber bundles with their cell rings each fill the same space (the 600-cell) but their fibers run Clifford parallel in different "directions"; great circle polygons in different fibrations are not Clifford parallel.[30]
Decagons

The fibrations of the 600-cell include 6 fibrations of its 72 great decagons: 6 fiber bundles of 12 great decagons.[lower-alpha 32] The 12 Clifford parallel decagons in each bundle are completely disjoint. Adjacent parallel decagons are spanned by edges of other great decagons.
Each fiber bundle[lower-alpha 44] delineates 20 helical rings of 30 tetrahedral cells each,[lower-alpha 31] with five rings nesting together around each decagon.[31] The Hopf map of this fibration is the icosahedron, where each of 12 vertices lifts to a great decagon, and each of 20 triangular faces lifts to a 30-cell ring.[lower-alpha 49] Each tetrahedral cell occupies only one of the 20 cell rings in each of the 6 fibrations. The tetrahedral cell contributes each of its 6 edges to a decagon in a different fibration, but contributes that edge to five distinct cell rings in the fibration.[lower-alpha 30]
The 12 great circles and 30-cell rings of the 600-cell's 6 characteristic Hopf fibrations make the 600-cell a geometric configuration of 30 "points" and 12 "lines" written as 302125. It is called the Schläfli double six configuration after Ludwig Schläfli,[33] the Swiss mathematician who discovered the 600-cell and the complete set of regular polytopes in n dimensions.[34]
Hexagons
The fibrations of the 24-cell include 4 fibrations of its 16 great hexagons: 4 fiber bundles of 4 great hexagons. The 4 Clifford parallel hexagons in each bundle are completely disjoint. Adjacent parallel hexagons are spanned by edges of other great hexagons. Each fiber bundle delineates 4 helical rings of 6 octahedral cells each, with three rings nesting together around each hexagon. Each octahedral cell occupies only one cell ring in each of the 4 fibrations. The octahedral cell contributes 3 of its 12 edges to 3 different Clifford parallel hexagons in each fibration, but contributes each edge to three distinct cell rings in the fibration.
The 600-cell contains 25 24-cells, and can be seen (10 different ways) as a compound of 5 disjoint 24-cells.[lower-alpha 14] It has 10 fibrations of its 200 great hexagons: 10 fiber bundles of 20 great hexagons. The 20 Clifford parallel hexagons in each bundle are completely disjoint. Adjacent parallel hexagons are spanned by edges of great decagons.[lower-alpha 45] Each fiber bundle delineates 20 helical rings of 6 octahedral cells each, with three rings nesting together around each hexagon. The Hopf map of this fibration is the dodecahedron, where the 20 vertices each lift to a bundle of great hexagons.[23] Each octahedral cell occupies only one of the 20 6-octahedron rings in each of the 10 fibrations. The 20 6-octahedron rings belong to 5 disjoint 24-cells of 4 6-octahedron rings each; each hexagonal fibration of the 600-cell consists of 5 disjoint 24-cells.
Squares
The fibrations of the 16-cell include 3 fibrations of its 6 great squares: 3 fiber bundles of 2 great squares. The 2 Clifford parallel squares in each bundle are completely disjoint. Adjacent parallel squares are spanned by edges of other great squares. Each fiber bundle delineates 2 helical rings of 8 tetrahedral cells each. Each tetrahedral cell occupies only one cell ring in each of the 3 fibrations. The tetrahedral cell contributes each of its 6 edges to a different square (contributing two opposite non-intersecting edges to each of the 3 fibrations), but contributes each edge to both of the two distinct cell rings in the fibration.
The 600-cell contains 75 16-cells, and can be seen (10 different ways) as a compound of 15 disjoint 16-cells. It has 15 fibrations of its 450 great squares: 15 fiber bundles of 30 great squares. The 30 Clifford parallel squares in each bundle are completely disjoint. Adjacent parallel squares are spanned by edges of great decagons.[lower-alpha 46] Each fiber bundle delineates 30 cell-disjoint helical rings of 8 tetrahedral cells each.[lower-alpha 51] The Hopf map of this fibration is the icosidodecahedron,[lower-alpha 23] where the 30 vertices each lift to a bundle of great squares.[24] Each tetrahedral cell occupies only one of the 30 8-tetrahedron rings in each of the 15 fibrations.
Clifford parallel cell rings
The densely packed helical cell rings[35][36][29] of fibrations are cell-disjoint, but they share vertices, edges and faces. Each fibration of the 600-cell can be seen as a dense packing of cell rings with the corresponding faces of adjacent cell rings face-bonded to each other.[lower-alpha 54] The same fibration can also be seen as a minimal sparse arrangement of fewer completely disjoint cell rings that do not touch at all.[lower-alpha 10]
The fibrations of great decagons can be seen (five different ways) as 4 completely disjoint 30-cell rings with spaces separating them, rather than as 20 face-bonded cell rings, by leaving out all but one cell ring of the five that meet at each decagon.[37] The five different ways you can do this are equivalent, in that all five correspond to the same discrete fibration (in the same sense that the 6 decagonal fibrations are equivalent, in that all 6 cover the same 600-cell). The 4 cell rings still constitute the complete fibration: they include all 12 Clifford parallel decagons, which visit all 120 vertices.[lower-alpha 55] This subset of 4 of 20 cell rings is dimensionally analogous[lower-alpha 2] to the subset of 12 of 72 decagons, in that both are sets of completely disjoint Clifford parallel polytopes which visit all 120 vertices.[lower-alpha 56] The subset of 4 of 20 cell rings is one of 5 fibrations within the fibration of 12 of 72 decagons: a fibration of a fibration. All the fibrations have this two level structure with subfibrations.
The fibrations of the 24-cell's great hexagons can be seen (three different ways) as 2 completely disjoint 6-cell rings with spaces separating them, rather than as 4 face-bonded cell rings, by leaving out all but one cell ring of the three that meet at each hexagon. Therefore each of the 10 fibrations of the 600-cell's great hexagons can be seen as 2 completely disjoint octahedral cell rings.
The fibrations of the 16-cell's great squares can be seen (two different ways) as a single 8-tetrahedral-cell ring with an adjacent cell-ring-sized empty space, rather than as 2 face-bonded cell rings, by leaving out one of the two cell rings that meet at each square. Therefore each of the 15 fibrations of the 600-cell's great squares can be seen as a single tetrahedral cell ring.[lower-alpha 51]
The sparse constructions of the 600-cell's fibrations correspond to lower-symmetry decompositions of the 600-cell, 24-cell or 16-cell with cells of different colors to distinguish the cell rings from the spaces between them.[lower-alpha 57] The particular lower-symmetry form of the 600-cell corresponding to the sparse construction of the great decagon fibrations is dimensionally analogous[lower-alpha 2] to the snub tetrahedron form of the icosahedron (which is the base[lower-alpha 49] of these fibrations on the 2-sphere). Each of the 20 Boerdijk-Coxeter cell rings[lower-alpha 31] is lifted from a corresponding face of the icosahedron.[lower-alpha 60]
Constructions
The 600-cell incorporates the geometries of every convex regular polytope in the first four dimensions, except the 5-cell, the 120-cell, and the polygons {7} and above.[41] Consequently, there are numerous ways to construct or deconstruct the 600-cell, but none of them are trivial. The construction of the 600-cell from its regular predecessor the 24-cell can be difficult to visualize.
Gosset's construction
Thorold Gosset discovered the semiregular 4-polytopes, including the snub 24-cell with 96 vertices, which falls between the 24-cell and the 600-cell in the sequence of convex 4-polytopes of increasing size and complexity in the same radius. Gosset's construction of the 600-cell from the 24-cell is in two steps, using the snub 24-cell as an intermediate form. In the first, more complex step (described elsewhere) the snub 24-cell is constructed by a special snub truncation of a 24-cell at the golden sections of its edges.[7] In the second step the 600-cell is constructed in a straightforward manner by adding 4-pyramids (vertices) to facets of the snub 24-cell.[42]
The snub 24-cell is a diminished 600-cell from which 24 vertices (and the cluster of 20 tetrahedral cells around each) have been truncated,[lower-alpha 26] leaving a "flat" icosahedral cell in place of each removed icosahedral pyramid.[lower-alpha 1] The snub 24-cell thus has 24 icosahedral cells and the remaining 120 tetrahedral cells. The second step of Gosset's construction of the 600-cell is simply the reverse of this diminishing: an icosahedral pyramid of 20 tetrahedral cells is placed on each icosahedral cell.
Constructing the unit-radius 600-cell from its precursor the unit-radius 24-cell by Gosset's method actually requires three steps. The 24-cell precursor to the snub-24 cell is not of the same radius: it is larger, since the snub-24 cell is its truncation. Starting with the unit-radius 24-cell, the first step is to reciprocate it around its midsphere to construct its outer canonical dual: a larger 24-cell, since the 24-cell is self-dual. That larger 24-cell can then be snub truncated into a unit-radius snub 24-cell.
Cell clusters
Since it is so indirect, Gosset's construction may not help us very much to directly visualize how the 600 tetrahedral cells fit together into a curved 3-dimensional surface envelope,[lower-alpha 27] or how they lie on the underlying surface envelope of the 24-cell's octahedral cells. For that it is helpful to build up the 600-cell directly from clusters of tetrahedral cells.
Most of us have difficulty visualizing the 600-cell from the outside in 4-space, or recognizing an outside view of the 600-cell due to our total lack of sensory experience in 4-dimensional spaces,[43] but we should be able to visualize the surface envelope of 600 cells from the inside because that volume is a 3-dimensional space that we could actually "walk around in" and explore.[44] In these exercises of building the 600-cell up from cell clusters, we are entirely within a 3-dimensional space, albeit a strangely small, closed curved space, in which we can go a mere ten edge lengths away in a straight line in any direction and return to our starting point.
Icosahedra

The vertex figure of the 600-cell is the icosahedron.[lower-alpha 1] Twenty tetrahedral cells meet at each vertex, forming an icosahedral pyramid whose apex is the vertex, surrounded by its base icosahedron. The 600-cell has a dihedral angle of 𝜋/3 + arccos(−1/4) ≈ 164.4775°.[46]
An entire 600-cell can be assembled from 24 such icosahedral pyramids (bonded face-to-face at 8 of the 20 faces of the icosahedron, colored yellow in the illustration), plus 24 clusters of 5 tetrahedral cells (four cells face-bonded around one) which fill the voids remaining between the icosahedra. Each icosahedron is face-bonded to each adjacent cluster of 5 cells by two blue faces that share an edge (which is also one of the six edges of the central tetrahedron of the five). Six clusters of 5 cells surround each icosahedron, and six icosahedra surround each cluster of 5 cells. Five tetrahedral cells surround each icosahedron edge: two from inside the icosahedral pyramid, and three from outside it.[lower-alpha 64]
The apexes of the 24 icosahedral pyramids are the vertices of a 24-cell inscribed in the 600-cell. The other 96 vertices (the vertices of the icosahedra) are the vertices of an inscribed snub 24-cell, which has exactly the same structure of icosahedra and tetrahedra described here, except that the icosahedra are not 4-pyramids filled by tetrahedral cells; they are only "flat" 3-dimensional icosahedral cells, because the central apical vertex is missing.
The 24-cell edges joining icosahedral pyramid apex vertices run through the centers of the yellow faces. Coloring the icosahedra with 8 yellow and 12 blue faces can be done in 5 distinct ways.[lower-alpha 65] Thus each icosahedral pyramid's apex vertex is a vertex of 5 distinct 24-cells,[lower-alpha 12] and the 120 vertices comprise 25 (not 5) 24-cells.[lower-alpha 9]
The icosahedra are face-bonded into geodesic "straight lines" by their opposite yellow faces, bent in the fourth dimension into a ring of 6 icosahedral pyramids. Their apexes are the vertices of a great circle hexagon. This hexagonal geodesic traverses a ring of 12 tetrahedral cells, alternately bonded face-to-face and vertex-to-vertex. The long diameter of each face-bonded pair of tetrahedra (each triangular bipyramid) is a hexagon edge (a 24-cell edge). There are 4 rings of 6 icosahedral pyramids intersecting at each apex-vertex, just as there are 4 cell-disjoint interlocking rings of 6 octahedra in the 24-cell (a hexagonal fibration).[lower-alpha 68]
The tetrahedral cells are face-bonded into triple helices, bent in the fourth dimension into rings of 30 tetrahedral cells.[lower-alpha 31] The three helices are geodesic "straight lines" of 10 edges: great circle decagons which run Clifford parallel[lower-alpha 33] to each other. Each tetrahedron, having six edges, participates in six different decagons[lower-alpha 30] and thereby in all 6 of the decagonal fibrations of the 600-cell.
The partitioning of the 600-cell into clusters of 20 cells and clusters of 5 cells is artificial, since all the cells are the same. One can begin by picking out an icosahedral pyramid cluster centered at any arbitrarily chosen vertex, so there are 120 overlapping icosahedra in the 600-cell.[lower-alpha 62] Their 120 apexes are each a vertex of five 24-vertex 24-cells, so there are 5*120/24 = 25 overlapping 24-cells.[lower-alpha 14]
Octahedra
There is another useful way to partition the 600-cell surface, into 24 clusters of 25 tetrahedral cells, which reveals more structure[51] and a direct construction of the 600-cell from its predecessor the 24-cell.
Begin with any one of the clusters of 5 cells (above), and consider its central cell to be the center object of a new larger cluster of tetrahedral cells. The central cell is the first section of the 600-cell beginning with a cell. By surrounding it with more tetrahedral cells, we can reach the deeper sections beginning with a cell.
First, note that a cluster of 5 cells consists of 4 overlapping pairs of face-bonded tetrahedra (triangular dipyramids) whose long diameter is a 24-cell edge (a hexagon edge) of length √1. Six more triangular dipyramids fit into the concavities on the surface of the cluster of 5,[lower-alpha 69] so the exterior chords connecting its 4 apical vertices are also 24-cell edges of length √1. They form a tetrahedron of edge length √1, which is the second section of the 600-cell beginning with a cell.[lower-alpha 70] There are 600 of these √1 tetrahedral sections in the 600-cell.
With the six triangular dipyamids fit into the concavities, there are 12 new cells and 6 new vertices in addition to the 5 cells and 8 vertices of the original cluster. The 6 new vertices form the third section of the 600-cell beginning with a cell, an octahedron of edge length √1, obviously the cell of a 24-cell.[lower-alpha 71] As partially filled so far (by 17 tetrahedral cells), this √1 octahedron has concave faces into which a short triangular pyramid fits; it has the same volume as a regular tetrahedral cell but an irregular tetrahedral shape.[lower-alpha 72] Each octahedron surrounds 1 + 4 + 12 + 8 = 25 tetrahedral cells: 17 regular tetrahedral cells plus 8 volumetrically equivalent tetrahedral cells each consisting of 6 one-sixth fragments from 6 different regular tetrahedral cells that each span three adjacent octahedral cells.[lower-alpha 73]
Thus the unit-radius 600-cell may be constructed directly from its predecessor,[lower-alpha 29] the unit-radius 24-cell, by placing on each of its octahedral facets a truncated[lower-alpha 74] irregular octahedral pyramid of 14 vertices[lower-alpha 75] constructed (in the above manner) from 25 regular tetrahedral cells of edge length 1/φ ≈ 0.618.
Union of two tori
There is yet another useful way to partition the 600-cell surface into clusters of tetrahedral cells, which reveals more structure[52] and the decagonal fibrations of the 600-cell. An entire 600-cell can be assembled around two rings of 5 icosahedral pyramids, bonded vertex-to-vertex into two geodesic "straight lines".

The 120-cell can be decomposed into two disjoint tori. Since it is the dual of the 600-cell, this same dual tori structure exists in the 600-cell, although it is somewhat more complex. The 10-cell geodesic path in the 120-cell corresponds to the 10-vertex decagon path in the 600-cell.[53]
Start by assembling five tetrahedra around a common edge. This structure looks somewhat like an angular "flying saucer". Stack ten of these, vertex to vertex, "pancake" style. Fill in the annular ring between each pair of "flying saucers" with 10 tetrahedra to form an icosahedron. You can view this as five vertex-stacked icosahedral pyramids, with the five extra annular ring gaps also filled in.[lower-alpha 76] The surface is the same as that of ten stacked pentagonal antiprisms: a triangular-faced column with a pentagonal cross-section.[54] Bent into a columnar ring this is a torus consisting of 150 cells, ten edges long, with 100 exposed triangular faces,[lower-alpha 77] 150 exposed edges, and 50 exposed vertices. Stack another tetrahedron on each exposed face. This will give you a somewhat bumpy torus of 250 cells with 50 raised vertices, 50 valley vertices, and 100 valley edges.[lower-alpha 78] The valleys are 10 edge long closed paths and correspond to other instances of the 10-vertex decagon path mentioned above (great circle decagons). These decagons spiral around the center core decagon,[lower-alpha 79] but mathematically they are all equivalent (they all lie in central planes).
Build a second identical torus of 250 cells that interlinks with the first. This accounts for 500 cells. These two tori mate together with the valley vertices touching the raised vertices, leaving 100 tetrahedral voids that are filled with the remaining 100 tetrahedra that mate at the valley edges. This latter set of 100 tetrahedra are on the exact boundary of the duocylinder and form a Clifford torus. They can be "unrolled" into a square 10×10 array. Incidentally this structure forms one tetrahedral layer in the tetrahedral-octahedral honeycomb. There are exactly 50 "egg crate" recesses and peaks on both sides that mate with the 250 cell tori. In this case into each recess, instead of an octahedron as in the honeycomb, fits a triangular bipyramid composed of two tetrahedra.
This decomposition of the 600-cell has symmetry 10,2+,10, order 400, the same symmetry as the grand antiprism.[55] The grand antiprism is just the 600-cell with the two above 150-cell tori removed, leaving only the single middle layer of 300 tetrahedra, dimensionally analogous[lower-alpha 2] to the 10-face belt of an icosahedron with the 5 top and 5 bottom faces removed (a pentagonal antiprism).[lower-alpha 80]
The two 150-cell tori each contain 6 Clifford parallel great decagons (five around one), and the two tori are Clifford parallel to each other, so together they constitute a complete fibration of 12 decagons that reaches all 120 vertices, despite filling only half the 600-cell with cells.
Boerdijk–Coxeter helix rings
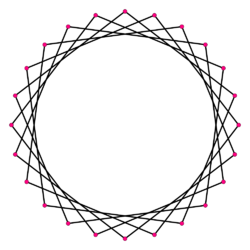
The 600-cell can also be partitioned into 20 cell-disjoint intertwining rings of 30 cells,[31] each ten edges long, forming a discrete Hopf fibration which fills the entire 600-cell.[56][57] Each ring of 30 face-bonded tetrahedra is a cylindrical Boerdijk–Coxeter helix bent into a ring in the fourth dimension.
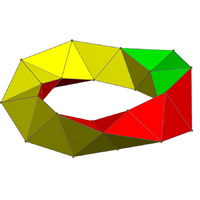 A single 30-tetrahedron Boerdijk–Coxeter helix ring within the 600-cell, seen in stereographic projection.[lower-alpha 31] |
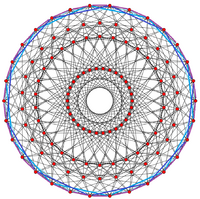 A 30-tetrahedron ring can be seen along the perimeter of this 30-gonal orthogonal projection of the 600-cell.[lower-alpha 41] |
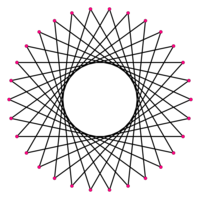 The 30-cell ring as a {30/11} polygram of 30 edges wound into a helix that twists around its axis 11 times. This projection along the axis of the 30-cell cylinder shows the 30 vertices 12° apart around the cylinder's circular cross section, with the edges connecting every 11th vertex on the circle.[lower-alpha 40] |
 The 30-vertex, 30-tetrahedron Boerdijk–Coxeter helix ring, cut and laid out flat in 3-dimensional space. Three cyan Clifford parallel great decagons bound the ring.[lower-alpha 32] They are bridged by a skew 30-gram helix of 30 magenta edges linking all 30 vertices: the Petrie polygon of the 600-cell.[lower-alpha 81] The 15 orange edges and 15 yellow edges form separate 15-gram helices, the edge-paths of isoclines. | ||
The 30-cell ring is the 3-dimensional space occupied by the 30 vertices of three cyan Clifford parallel great decagons that lie adjacent to each other, 36° = 𝜋/5 = one 600-cell edge length apart at all their vertex pairs.[lower-alpha 82] The 30 magenta edges joining these vertex pairs form a helical triacontagram, a skew 30-gram spiral of 30 edge-bonded triangular faces, that is the Petrie polygon of the 600-cell.[lower-alpha 81] The dual of the 30-cell ring (the skew 30-gon made by connecting its cell centers) is the Petrie polygon of the 120-cell, the 600-cell's dual polytope.[lower-alpha 50] The central axis of the 30-cell ring is a great 30-gon geodesic that passes through the center of 30 faces, but does not intersect any vertices.[lower-alpha 41]
The 15 orange edges and 15 yellow edges form separate 15-gram helices. Each orange or yellow edge crosses between two cyan great decagons. Successive orange or yellow edges of these 15-gram helices do not lie on the same great circle; they lie in different central planes inclined at 36° = 𝝅/5 to each other.[lower-alpha 47] Each 15-gram helix is noteworthy as the edge-path of an isocline, the geodesic path of an isoclinic rotation.[lower-alpha 42] The isocline is a circular curve which intersects every second vertex of the 15-gram, missing the vertex in between. A single isocline runs twice around each orange (or yellow) 15-gram through every other vertex, hitting half the vertices on the first loop and the other half of them on the second loop. The two connected loops forms a single Möbius loop, a skew {15/2} pentadecagram. The pentadecagram is not shown in these illustrations (but see below), because its edges are invisible chords between vertices which are two orange (or two yellow) edges apart, and no chords are shown in these illustrations. Although the 30 vertices of the 30-cell ring do not lie in one great 30-gon central plane,[lower-alpha 82] these invisible pentadecagram isoclines are true geodesic circles of a special kind, that wind through all four dimensions rather than lying in a 2-dimensional plane as an ordinary geodesic great circle does.[lower-alpha 83]
Five of these 30-cell helices nest together and spiral around each of the 10-vertex decagon paths, forming the 150-cell torus described in the grand antiprism decomposition above.[55] Thus every great decagon is the center core decagon of a 150-cell torus.[lower-alpha 84] The 600-cell may be decomposed into 20 30-cell rings, or into two 150-cell tori and 10 30-cell rings, but not into four 150-cell tori of this kind.[lower-alpha 85] The 600-cell can be decomposed into four 150-cell tori of a different kind.[lower-alpha 86]
Radial golden triangles
The 600-cell can be constructed radially from 720 golden triangles of edge lengths √0.𝚫 √1 √1 which meet at the center of the 4-polytope, each contributing two √1 radii and a √0.𝚫 edge.[lower-alpha 23] They form 1200 triangular pyramids with their apexes at the center: irregular tetrahedra with equilateral √0.𝚫 bases (the faces of the 600-cell). These form 600 tetrahedral pyramids with their apexes at the center: irregular 5-cells with regular √0.𝚫 tetrahedron bases (the cells of the 600-cell).
Characteristic orthoscheme
| Characteristics of the 600-cell[59] | |||||
|---|---|---|---|---|---|
| edge[60] | arc | dihedral[61] | |||
| 𝒍 | [math]\displaystyle{ \tfrac{1}{\phi} \approx 0.618 }[/math] | 36° | [math]\displaystyle{ \tfrac{\pi}{5} }[/math] | 164°29′ | [math]\displaystyle{ \pi-2\text{𝟁} }[/math] |
| 𝟀 | [math]\displaystyle{ \sqrt{\tfrac{2}{3\phi^2}} \approx 0.505 }[/math] | 22°15′20″ | [math]\displaystyle{ \tfrac{\pi}{3} - \text{𝜼} }[/math] | 60° | [math]\displaystyle{ \tfrac{\pi}{3} }[/math] |
| 𝝉[lower-alpha 87] | [math]\displaystyle{ \sqrt{\tfrac{1}{2\phi^2}} \approx 0.437 }[/math] | 18° | [math]\displaystyle{ \tfrac{\pi}{10} }[/math] | 36° | [math]\displaystyle{ \tfrac{\pi}{5} }[/math] |
| 𝟁 | [math]\displaystyle{ \sqrt{\tfrac{1}{6\phi^2}} \approx 0.252 }[/math] | 17°44′40″ | [math]\displaystyle{ \text{𝜼} - \tfrac{\pi}{6} }[/math] | 60° | [math]\displaystyle{ \tfrac{\pi}{3} }[/math] |
| [math]\displaystyle{ _0R^3/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{3}{4\phi^2}} \approx 0.535 }[/math] | 22°15′20″ | [math]\displaystyle{ \tfrac{\pi}{3} - \text{𝜼} }[/math] | 90° | [math]\displaystyle{ \tfrac{\pi}{2} }[/math] |
| [math]\displaystyle{ _1R^3/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{4\phi^2}} \approx 0.309 }[/math] | 18° | [math]\displaystyle{ \tfrac{\pi}{10} }[/math] | 90° | [math]\displaystyle{ \tfrac{\pi}{2} }[/math] |
| [math]\displaystyle{ _2R^3/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{12\phi^2}} \approx 0.178 }[/math] | 17°44′40″ | [math]\displaystyle{ \text{𝜼} - \tfrac{\pi}{6} }[/math] | 90° | [math]\displaystyle{ \tfrac{\pi}{2} }[/math] |
| [math]\displaystyle{ _0R^4/l }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ _1R^4/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{5 + \sqrt{5}}{8}} \approx 0.951 }[/math] | ||||
| [math]\displaystyle{ _2R^4/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{\phi^2}{3}} \approx 0.934 }[/math] | ||||
| [math]\displaystyle{ _3R^4/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{\phi^4}{8}} \approx 0.926 }[/math] | ||||
| [math]\displaystyle{ \text{𝜼} }[/math] | 37°44′40″ | [math]\displaystyle{ \tfrac{\text{arc sec }4}{2} }[/math] | |||
Every regular 4-polytope has its characteristic 4-orthoscheme, an irregular 5-cell.[lower-alpha 88]
The characteristic 5-cell of the regular 600-cell is represented by the Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , which can be read as a list of the dihedral angles between its mirror facets.
It is an irregular tetrahedral pyramid based on the characteristic tetrahedron of the regular tetrahedron.
The regular 600-cell is subdivided by its symmetry hyperplanes into 14400 instances of its characteristic 5-cell that all meet at its center.[lower-alpha 52]
, which can be read as a list of the dihedral angles between its mirror facets.
It is an irregular tetrahedral pyramid based on the characteristic tetrahedron of the regular tetrahedron.
The regular 600-cell is subdivided by its symmetry hyperplanes into 14400 instances of its characteristic 5-cell that all meet at its center.[lower-alpha 52]
The characteristic 5-cell (4-orthoscheme) has four more edges than its base characteristic tetrahedron (3-orthoscheme), joining the four vertices of the base to its apex (the fifth vertex of the 4-orthoscheme, at the center of the regular 600-cell).[lower-alpha 89] If the regular 600-cell has unit radius and edge length [math]\displaystyle{ \text{𝒍} = \tfrac{1}{\phi} \approx 0.618 }[/math], its characteristic 5-cell's ten edges have lengths [math]\displaystyle{ \sqrt{\tfrac{2}{3\phi^2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{2\phi^2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{6\phi^2}} }[/math] around its exterior right-triangle face (the edges opposite the characteristic angles 𝟀, 𝝉, 𝟁),[lower-alpha 87] plus [math]\displaystyle{ \sqrt{\tfrac{3}{4\phi^2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{4\phi^2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{12\phi^2}} }[/math] (the other three edges of the exterior 3-orthoscheme facet the characteristic tetrahedron, which are the characteristic radii of the regular tetrahedron), plus [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ \sqrt{\tfrac{5 + \sqrt{5}}{8}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{\phi^2}{3}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{\phi^4}{8}} }[/math] (edges which are the characteristic radii of the 600-cell). The 4-edge path along orthogonal edges of the orthoscheme is [math]\displaystyle{ \sqrt{\tfrac{1}{2\phi^2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{6\phi^2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{4\phi^2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{\phi^4}{8}} }[/math], first from a 600-cell vertex to a 600-cell edge center, then turning 90° to a 600-cell face center, then turning 90° to a 600-cell tetrahedral cell center, then turning 90° to the 600-cell center.
Reflections
The 600-cell can be constructed by the reflections of its characteristic 5-cell in its own facets (its tetrahedral mirror walls).[lower-alpha 90] Reflections and rotations are related: a reflection in an even number of intersecting mirrors is a rotation.[63][64] For example, a full isoclinic rotation of the 600-cell in decagonal invariant planes takes each of the 120 vertices through 15 vertices and back to itself, on a skew pentadecagram2 geodesic isocline of circumference 5𝝅 that winds around the 3-sphere, as each great decagon rotates (like a wheel) and also tilts sideways (like a coin flipping) with the completely orthogonal plane.[lower-alpha 91] Any set of four orthogonal pairs of antipodal vertices (the 8 vertices of one of the 75 inscribed 16-cells)[lower-alpha 55] performing such an orbit visits 15 * 8 = 120 distinct vertices and generates the 600-cell sequentially in one full isoclinic rotation, just as any single characteristic 5-cell reflecting itself in its own mirror walls generates the 120 vertices simultaneously by reflection.[lower-alpha 67]
Weyl orbits
Another construction method uses quaternions and the Icosahedral symmetry of Weyl group orbits [math]\displaystyle{ O(\Lambda)=W(H_4)=I }[/math] of order 120.[66] The following are the orbits of weights of D4 under the Weyl group W(D4):
- O(0100) : T = {±1,±e1,±e2,±e3,(±1±e1±e2±e3)/2}
- O(1000) : V1
- O(0010) : V2
- O(0001) : V3
With quaternions [math]\displaystyle{ (p,q) }[/math] where [math]\displaystyle{ \bar p }[/math] is the conjugate of [math]\displaystyle{ p }[/math] and [math]\displaystyle{ [p,q]:r\rightarrow r'=prq }[/math] and [math]\displaystyle{ [p,q]^*:r\rightarrow r''=p\bar rq }[/math], then the Coxeter group [math]\displaystyle{ W(H_4)=\lbrace[p,\bar p] \oplus [p,\bar p]^*\rbrace }[/math] is the symmetry group of the 600-cell and the 120-cell of order 14400.
Given [math]\displaystyle{ p \in T }[/math] such that [math]\displaystyle{ \bar p=\pm p^4, \bar p^2=\pm p^3, \bar p^3=\pm p^2, \bar p^4=\pm p }[/math] and [math]\displaystyle{ p^\dagger }[/math] as an exchange of [math]\displaystyle{ -1/\varphi \leftrightarrow \varphi }[/math] within [math]\displaystyle{ p }[/math], we can construct:
- the snub 24-cell [math]\displaystyle{ S=\sum_{i=1}^4\oplus p^i T }[/math]
- the 600-cell [math]\displaystyle{ I=T+S=\sum_{i=0}^4\oplus p^i T }[/math]
- the 120-cell [math]\displaystyle{ J=\sum_{i,j=0}^4\oplus p^i\bar p^{\dagger j}T' }[/math]
Rotations
The regular convex 4-polytopes are an expression of their underlying symmetry which is known as SO(4), the group of rotations[67] about a fixed point in 4-dimensional Euclidean space.[lower-alpha 102]
The 600-cell is generated by isoclinic rotations[lower-alpha 42] of the 24-cell by 36° = 𝜋/5 (the arc of one 600-cell edge length).[lower-alpha 104]
Twenty-five 24-cells
There are 25 inscribed 24-cells in the 600-cell.[lower-alpha 94] Therefore there are also 25 inscribed snub 24-cells, 75 inscribed tesseracts and 75 inscribed 16-cells.[lower-alpha 9]
The 8-vertex 16-cell has 4 long diameters inclined at 90° = 𝜋/2 to each other, often taken as the 4 orthogonal axes or basis of the coordinate system.[lower-alpha 15]
The 24-vertex 24-cell has 12 long diameters inclined at 60° = 𝜋/3 to each other: 3 disjoint sets of 4 orthogonal axes, each set comprising the diameters of one of 3 inscribed 16-cells, isoclinically rotated by 𝜋/3 with respect to each other.[lower-alpha 105]
The 120-vertex 600-cell has 60 long diameters: not just 5 disjoint sets of 12 diameters, each comprising one of 5 inscribed 24-cells (as we might suspect by analogy), but 25 distinct but overlapping sets of 12 diameters, each comprising one of 25 inscribed 24-cells.[72] There are 5 disjoint 24-cells in the 600-cell, but not just 5: there are 10 different ways to partition the 600-cell into 5 disjoint 24-cells.[lower-alpha 13]
Like the 16-cells and 8-cells inscribed in the 24-cell, the 25 24-cells inscribed in the 600-cell are mutually isoclinic polytopes. The rotational distance between inscribed 24-cells is always 𝜋/5 in each invariant plane of rotation.[lower-alpha 103]
Five 24-cells are disjoint because they are Clifford parallel: their corresponding vertices are 𝜋/5 apart on two non-intersecting Clifford parallel[lower-alpha 33] decagonal great circles (as well as 𝜋/5 apart on the same decagonal great circle).[lower-alpha 32] An isoclinic rotation of decagonal planes by 𝜋/5 takes each 24-cell to a disjoint 24-cell (just as an isoclinic rotation of hexagonal planes by 𝜋/3 takes each 16-cell to a disjoint 16-cell).[lower-alpha 106] Each isoclinic rotation occurs in two chiral forms: there are 4 disjoint 24-cells to the left of each 24-cell, and another 4 disjoint 24-cells to its right.[lower-alpha 108] The left and right rotations reach different 24-cells; therefore each 24-cell belongs to two different sets of five disjoint 24-cells.
All Clifford parallel polytopes are isoclinic, but not all isoclinic polytopes are Clifford parallels (completely disjoint objects).[lower-alpha 109] Each 24-cell is isoclinic and Clifford parallel to 8 others, and isoclinic but not Clifford parallel to 16 others.[lower-alpha 7] With each of the 16 it shares 6 vertices: a hexagonal central plane.[lower-alpha 12] Non-disjoint 24-cells are related by a simple rotation by 𝜋/5 in an invariant plane intersecting only two vertices of the 600-cell,[lower-alpha 48] a rotation in which the completely orthogonal fixed plane is their common hexagonal central plane. They are also related by an isoclinic rotation in which both planes rotate by 𝜋/5.[lower-alpha 111]
There are two kinds of 𝜋/5 isoclinic rotations which take each 24-cell to another 24-cell.[lower-alpha 106] Disjoint 24-cells are related by a 𝜋/5 isoclinic rotation of an entire fibration of 12 Clifford parallel decagonal invariant planes. (There are 6 such sets of fibers, and a right or a left isoclinic rotation possible with each set, so there are 12 such distinct rotations.)[lower-alpha 108] Non-disjoint 24-cells are related by a 𝜋/5 isoclinic rotation of an entire fibration of 20 Clifford parallel hexagonal invariant planes.[lower-alpha 113] (There are 10 such sets of fibers, so there are 20 such distinct rotations.)[lower-alpha 110]
On the other hand, each of the 10 sets of five disjoint 24-cells is Clifford parallel because its corresponding great hexagons are Clifford parallel. (24-cells do not have great decagons.) The 16 great hexagons in each 24-cell can be divided into 4 sets of 4 non-intersecting Clifford parallel geodesics, each set of which covers all 24 vertices of the 24-cell. The 200 great hexagons in the 600-cell can be divided into 10 sets of 20 non-intersecting Clifford parallel geodesics, each set of which covers all 120 vertices and constitutes a discrete hexagonal fibration. Each of the 10 sets of 20 disjoint hexagons can be divided into five sets of 4 disjoint hexagons, each set of 4 covering a disjoint 24-cell. Similarly, the corresponding great squares of disjoint 24-cells are Clifford parallel.
Rotations on polygram isoclines
The regular convex 4-polytopes each have their characteristic kind of right (and left) isoclinic rotation, corresponding to their characteristic kind of discrete Hopf fibration of great circles.[lower-alpha 59] For example, the 600-cell can be fibrated six different ways into a set of Clifford parallel great decagons, so the 600-cell has six distinct right (and left) isoclinic rotations in which those great decagon planes are invariant planes of rotation. We say these isoclinic rotations are characteristic of the 600-cell because the 600-cell's edges lie in their invariant planes. These rotations only emerge in the 600-cell, although they are also found in larger regular polytopes (the 120-cell) which contain inscribed instances of the 600-cell.
Just as the geodesic polygons (decagons or hexagons or squares) in the 600-cell's central planes form fiber bundles of Clifford parallel great circles, the corresponding geodesic skew polygrams (which trace the paths on the Clifford torus of vertices under isoclinic rotation)[76] form fiber bundles of Clifford parallel isoclines: helical circles which wind through all four dimensions.[lower-alpha 42] Since isoclinic rotations are chiral, occurring in left-handed and right-handed forms, each polygon fiber bundle has corresponding left and right polygram fiber bundles.[77] All the fiber bundles are aspects of the same discrete Hopf fibration, because the fibration is the various expressions of the same distinct left-right pair of isoclinic rotations.
Cell rings are another expression of the Hopf fibration. Each discrete fibration has a set of cell-disjoint cell rings that tesselates the 4-polytope.[lower-alpha 54] The isoclines in each chiral bundle spiral around each other: they are axial geodesics of the rings of face-bonded cells. The Clifford parallel cell rings of the fibration nest into each other, pass through each other without intersecting in any cells, and exactly fill the 600-cell with their disjoint cell sets.
Isoclinic rotations rotate a rigid object's vertices along parallel paths, each vertex circling within two orthogonal moving great circles, the way a loom weaves a piece of fabric from two orthogonal sets of parallel fibers. A bundle of Clifford parallel great circle polygons and a corresponding bundle of Clifford parallel skew polygram isoclines are the warp and woof of the same distinct left or right isoclinic rotation, which takes Clifford parallel great circle polygons to each other, flipping them like coins and rotating them through a Clifford parallel set of central planes. Meanwhile, because the polygons are also rotating individually like wheels, vertices are displaced along helical Clifford parallel isoclines (the chords of which form the skew polygram), through vertices which lie in successive Clifford parallel polygons.[lower-alpha 58]
In the 600-cell, each family of isoclinic skew polygrams (moving vertex paths in the decagon {10}, hexagon {6}, or square {4} great polygon rotations) can be divided into bundles of non-intersecting Clifford parallel polygram isoclines.[78] The isocline bundles occur in pairs of left and right chirality; the isoclines in each rotation act as chiral objects, as does each distinct isoclinic rotation itself.[lower-alpha 53] Each fibration contains an equal number of left and right isoclines, in two disjoint bundles, which trace the paths of the 600-cell's vertices during the fibration's left or right isoclinic rotation respectively. Each left or right fiber bundle of isoclines by itself constitutes a discrete Hopf fibration which fills the entire 600-cell, visiting all 120 vertices just once. It is a different bundle of fibers than the bundle of Clifford parallel polygon great circles, but the two fiber bundles describe the same discrete fibration because they enumerate those 120 vertices together in the same distinct right (or left) isoclinic rotation, by their intersection as a fabric of cross-woven parallel fibers.
Each isoclinic rotation involves pairs of completely orthogonal invariant central planes of rotation, which both rotate through the same angle. There are two ways they can do this: by both rotating in the "same" direction, or by rotating in "opposite" directions (according to the right hand rule by which we conventionally say which way is "up" on each of the 4 coordinate axes). The right polygram and right isoclinic rotation conventionally correspond to invariant pairs rotating in the same direction; the left polygram and left isoclinic rotation correspond to pairs rotating in opposite directions.[74] Left and right isoclines are different paths that go to different places. In addition, each distinct isoclinic rotation (left or right) can be performed in a positive or negative direction along the circular parallel fibers.
A fiber bundle of Clifford parallel isoclines is the set of helical vertex circles described by a distinct left or right isoclinic rotation. Each moving vertex travels along an isocline contained within a (moving) cell ring. While the left and right isoclinic rotations each double-rotate the same set of Clifford parallel invariant planes of rotation, they step through different sets of great circle polygons because left and right isoclinic rotations hit alternate vertices of the great circle {2p} polygon (where p is a prime ≤ 5).[lower-alpha 117] The left and right rotation share the same Hopf bundle of {2p} polygon fibers, which is both a left and right bundle, but they have different bundles of {p} polygons[79] because the discrete fibers are opposing left and right {p} polygons inscribed in the {2p} polygon.[lower-alpha 118]
A simple rotation is direct and local, taking some vertices to adjacent vertices along great circles, and some central planes to other central planes within the same hyperplane.[lower-alpha 119] In a simple rotation, there is just a single pair of completely orthogonal invariant central planes of rotation; it does not constitute a fibration.
An isoclinic rotation is diagonal and global, taking all the vertices to non-adjacent vertices (two or more edge-lengths away)[lower-alpha 95] along diagonal isoclines, and all the central plane polygons to Clifford parallel polygons (of the same kind). A left-right pair of isoclinic rotations constitutes a discrete fibration. All the Clifford parallel central planes of the fibration are invariant planes of rotation, separated by two equal angles and lying in different hyperplanes.[lower-alpha 47] The diagonal isocline[lower-alpha 96] is a shorter route between the non-adjacent vertices than the multiple simple routes between them available along edges: it is the shortest route on the 3-sphere, the geodesic.
Decagons and 5𝝅 polygrams
The fibrations of the 600-cell include 6 fibrations of its 72 great decagons: 6 fiber bundles of 12 great decagons,[lower-alpha 32] each delineating 20 chiral cell rings of 30 tetrahedral cells each,[lower-alpha 31] with three great decagons bounding each cell ring, and five cell rings nesting together around each decagon. The 12 Clifford parallel decagons in each bundle are completely disjoint. Adjacent parallel decagons are spanned by edges of other great decagons.[lower-alpha 44] Each fibration corresponds to a distinct left (and right) isoclinic rotation of the 600-cell in 12 great decagon invariant planes on 5𝝅 isoclines.
The bundle of 12 Clifford parallel decagon fibers is divided into a bundle of 12 left pentagon fibers and a bundle of 12 right pentagon fibers, with each left-right pair of pentagons inscribed in a decagon.[80] 12 great polygons comprise a fiber bundle covering all 120 vertices in a discrete Hopf fibration. There are 20 cell-disjoint 30-cell rings in the fibration, but only 4 completely disjoint 30-cell rings.[lower-alpha 10] The 600-cell has six such discrete decagonal fibrations, and each is the domain (container) of a unique left-right pair of isoclinic rotations (left and right fiber bundles of 12 great pentagons).[lower-alpha 120] Each great decagon belongs to just one fibration,[79] but each 30-cell ring belongs to 5 of the six fibrations (and is completely disjoint from 1 other fibration). The 600-cell contains 72 great decagons, divided among six fibrations, each of which is a set of 20 cell-disjoint 30-cell rings (4 completely disjoint 30-cell rings), but the 600-cell has only 20 distinct 30-cell rings altogether. Each 30-cell ring contains 3 of the 12 Clifford parallel decagons in each of 5 fibrations, and 30 of the 120 vertices.
In these decagonal isoclinic rotations, vertices travel along isoclines which follow the edges of hexagons,[23] advancing a pythagorean distance of one hexagon edge in each double 36°×36° rotational unit.[lower-alpha 113] In an isoclinic rotation, each successive hexagon edge travelled lies in a different great hexagon, so the isocline describes a skew polygram, not a polygon. In a 60°×60° isoclinic rotation (as in the 24-cell's characteristic hexagonal rotation, and below in the hexagonal rotations of the 600-cell) this polygram is a hexagram: the isoclinic rotation follows a 6-edge circular path, just as a simple hexagonal rotation does, although it takes two revolutions to enumerate all the vertices in it, because the isocline is a double loop through every other vertex, and its chords are √3 chords of the hexagon instead of √1 hexagon edges.[lower-alpha 122] But in the 600-cell's 36°×36° characteristic decagonal rotation, successive great hexagons are closer together and more numerous, and the isocline polygram formed by their 15 hexagon edges is a pentadecagram (15-gram).[lower-alpha 91] It is not only not the same period as the hexagon or the simple decagonal rotation, it is not even an integer multiple of the period of the hexagon, or the decagon, or either's simple rotation. Only the compound {30/4}=2{15/2} triacontagram (30-gram), which is two 15-grams rotating in parallel (a black and a white), is a multiple of them all, and so constitutes the rotational unit of the decagonal isoclinic rotation.[lower-alpha 117]
In the 30-cell ring, the non-adjacent vertices linked by isoclinic rotations are two edge-lengths apart, with three other vertices of the ring lying between them.[lower-alpha 124] The two non-adjacent vertices are linked by a √1 chord of the isocline which is a great hexagon edge (a 24-cell edge). The √1 chords of the 30-cell ring (without the √0.𝚫 600-cell edges) form a skew triacontagram{30/4}=2{15/2} which contains 2 disjoint {15/2} Möbius double loops, a left-right pair of pentadecagram2 isoclines. Each left (or right) bundle of 12 pentagon fibers is crossed by a left (or right) bundle of 8 Clifford parallel pentadecagram fibers. Each distinct 30-cell ring has 2 double-loop pentadecagram isoclines running through its even or odd (black or white) vertices respectively.[lower-alpha 99] The pentadecagram helices have no inherent chirality, but each acts as either a left or right isocline in any distinct isoclinic rotation.[lower-alpha 116] The 2 pentadecagram fibers belong to the left and right fiber bundles of 5 different fibrations.
At each vertex, there are six great decagons and six pentadecagram isoclines (six black or six white) that cross at the vertex.[lower-alpha 128] Eight pentadecagram isoclines (four black and four white) comprise a unique right (or left) fiber bundle of isoclines covering all 120 vertices in the distinct right (or left) isoclinic rotation. Each fibration has a unique left and right isoclinic rotation, and corresponding unique left and right fiber bundles of 12 pentagons and 8 pentadecagram isoclines. There are only 20 distinct black isoclines and 20 distinct white isoclines in the 600-cell. Each distinct isocline belongs to 5 fiber bundles.
| Three sets of 30-cell ring chords from the same orthogonal projection viewpoint | |||
|---|---|---|---|
| Pentadecagram {15/2} | Triacontagram {30/4}=2{15/2} | Triacontagram {30/6}=6{5} | |
| All edges are pentadecagram isocline chords of length √1, which are also great hexagon edges of 24-cells inscribed in the 600-cell. | Only great pentagon edges of length √1.𝚫 ≈ 1.176. | ||
|

|
| |
| A single black (or white) isocline is a Möbius double loop skew pentadecagram {15/2} of circumference 5𝝅.[lower-alpha 91] The √1 chords are 24-cell edges (hexagon edges) from different inscribed 24-cells. These chords are invisible (not shown) in the 30-cell ring illustration, where they join opposite vertices of two face-bonded tetrahedral cells that are two orange edges apart or two yellow edges apart. | The 30-cell ring as a skew compound of two disjoint pentadecagram {15/2} isoclines (a black-white pair, shown here as orange-yellow).[lower-alpha 99] The √1 chords of the isoclines link every 4th vertex of the 30-cell ring in a straight chord under two orange edges or two yellow edges. The doubly-curved isocline is the geodesic (shortest path) between those vertices; they are also two edges apart by three different angled paths along the edges of the face-bonded tetrahedra. | Each pentadecagram isocline (at left) intersects all six great pentagons (above) in two or three vertices. The pentagons lie on flat 2𝝅 great circles in the decagon invariant planes of rotation. The pentadecagrams are not flat: they are helical 5𝝅 isocline circles whose 15 chords lie in successive great hexagon planes inclined at 𝝅/5 = 36° to each other. The isocline circle is said to be twisting either left or right with the rotation, but all such pentadecagrams are directly congruent, each acting as a left or right isocline in different fibrations. | |
| No 600-cell edges appear in these illustrations, only invisible interior chords of the 600-cell. In this article, they should all properly be drawn as dashed lines. | |||
Two 15-gram double-loop isoclines are axial to each 30-cell ring. The 30-cell rings are chiral; each fibration contains 10 right (clockwise-spiraling) rings and 10 left (counterclockwise spiraling) rings, but the two isoclines in each 3-cell ring are directly congruent.[lower-alpha 100] Each acts as a left (or right) isocline a left (or right) rotation, but has no inherent chirality.[lower-alpha 116] The fibration's 20 left and 20 right 15-grams altogether contain 120 disjoint open pentagrams (60 left and 60 right), the open ends of which are adjacent 600-cell vertices (one √0.𝚫 edge-length apart). The 30 chords joining the isocline's 30 vertices are √1 hexagon edges (24-cell edges), connecting 600-cell vertices which are two 600-cell √0.𝚫 edges apart on a decagon great circle. [lower-alpha 97] These isocline chords are both hexagon edges and pentagram edges.
The 20 Clifford parallel isoclines (30-cell ring axes) of each left (or right) isocline bundle do not intersect each other. Either distinct decagonal isoclinic rotation (left or right) rotates all 120 vertices (and all 600 cells), but pentadecagram isoclines and pentagons are connected such that vertices alternate as 60 black and 60 white vertices (and 300 black and 300 white cells), like the black and white squares of the chessboard.[lower-alpha 127] In the course of the rotation, the vertices on a left (or right) isocline rotate within the same 15-vertex black (or white) isocline, and the cells rotate within the same black (or white) 30-cell ring.
Hexagons and 4𝝅 polygrams
The fibrations of the 600-cell include 10 fibrations of its 200 great hexagons: 10 fiber bundles of 20 great hexagons. The 20 Clifford parallel hexagons in each bundle are completely disjoint. Adjacent parallel hexagons are spanned by edges of great decagons.[lower-alpha 45] Each fibration corresponds to a distinct left (and right) isoclinic rotation of the 600-cell in 20 great hexagon invariant planes on 4𝝅 isoclines.
Each fiber bundle delineates 20 disjoint directly congruent cell rings of 6 octahedral cells each, with three cell rings nesting together around each hexagon. The bundle of 20 Clifford parallel hexagon fibers is divided into a bundle of 20 black √3 great triangle fibers and a bundle of 20 white great triangle fibers, with a black and a white triangle inscribed in each hexagon and 6 black and 6 white triangles in each 6-octahedron ring. The black or white triangles are joined by three intersecting black or white isoclines, each of which is a special kind of helical great circle[lower-alpha 122] through the corresponding vertices in 10 Clifford parallel black (or white) great triangles. The 10 √1.𝚫 chords of each isocline form a skew decagram {10/3}, 10 great pentagon edges joined end-to-end in a helical loop, winding 3 times around the 600-cell through all four dimensions rather than lying flat in a central plane. Each pair of black and white isoclines (intersecting antipodal great hexagon vertices) forms a compound 20-gon icosagram {20/6}=2{10/3}.
Notice the relation between the 24-cell's characteristic rotation in great hexagon invariant planes (on hexagram isoclines), and the 600-cell's own version of the rotation of great hexagon planes (on decagram isoclines). They are exactly the same isoclinic rotation: they have the same isocline. They have different numbers of the same isocline, and the 600-cell's √1.𝚫 isocline chord is shorter than the 24-cell's (√3) isocline chord, because the isocline intersects more vertices in the 600-cell (10) than it does in the 24-cell (6), but both Clifford polygrams have a 4𝝅 circumference.[lower-alpha 130]
Squares and 8𝝅 polygrams
The fibrations of the 600-cell include 15 fibrations of its 450 great squares: 15 fiber bundles of 30 great squares. The 30 Clifford parallel squares in each bundle are completely disjoint. Adjacent parallel squares are spanned by edges of great decagons.[lower-alpha 46] Each fibration corresponds to a distinct left (and right) isoclinic rotation of the 600-cell in 30 great square invariant planes (15 completely orthogonal pairs) on 8𝝅 isoclines.
Each fiber bundle delineates 30 chiral cell rings of 8 tetrahedral cells each,[lower-alpha 51] with a left and right cell ring nesting together to fill each of the 15 disjoint 16-cells inscribed in the 600-cell. Axial to each 8-tetrahedron ring is a special kind of helical great circle, an isocline.[lower-alpha 42] In a left (or right) isoclinic rotation of the 600-cell in great square invariant planes, all the vertices circulate on one of 15 Clifford parallel isoclines.
The 30 Clifford parallel squares in each bundle are joined by four Clifford parallel 24-gram isoclines (one through each vertex), each of which intersects one vertex in 24 of the 30 squares, and all 24 vertices of just one of the 600-cell's 25 24-cells. Each isocline is a 24-gram circuit intersecting all 25 24-cells, 24 of them just once and one of them 24 times. The 24 vertices in each 24-gram isocline comprise a unique 24-cell; there are 25 such distinct isoclines in the 600-cell. Each isocline is a skew {24/5} 24-gram, 24 φ = √2.𝚽 chords joined end-to-end in a helical loop, winding 5 times around one 24-cell through all four dimensions rather than lying flat in a central plane. Adjacent vertices of the 24-cell are one √1 chord apart, and 5 φ chords apart on its isocline. A left (or right) isoclinic rotation through 720° takes each 24-cell to and through every other 24-cell.
Notice the relations between the 16-cell's rotation of just 2 invariant great square planes, the 24-cell's rotation in 6 Clifford parallel great squares, and this rotation of the 600-cell in 30 Clifford parallel great squares. These three rotations are the same rotation, taking place on exactly the same kind of isocline circles, which happen to intersect more vertices in the 600-cell (24) than they do in the 16-cell (8).[lower-alpha 131] In the 16-cell's rotation the distance between vertices on an isocline curve is the √4 diameter axis. In the 600-cell vertices are closer together, and its √2.𝚽 = φ chord is the distance between adjacent vertices on the same isocline, but all three Clifford polygrams have an 8𝝅 circumference.
As a configuration
This configuration matrix[84] represents the 600-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 600-cell. The non-diagonal numbers say how many of the column's element occur in or at the row's element.
[math]\displaystyle{ \begin{bmatrix}\begin{matrix}120 & 12 & 30 & 20 \\ 2 & 720 & 5 & 5 \\ 3 & 3 & 1200 & 2 \\ 4 & 6 & 4 & 600 \end{matrix}\end{bmatrix} }[/math]
Here is the configuration expanded with k-face elements and k-figures. The diagonal element counts are the ratio of the full Coxeter group order, 14400, divided by the order of the subgroup with mirror removal.
| H4 | k-face | fk | f0 | f1 | f2 | f3 | k-fig | Notes | |
|---|---|---|---|---|---|---|---|---|---|
| H3 | ( ) | f0 | 120 | 12 | 30 | 20 | {3,5} | H4/H3 = 14400/120 = 120 | |
| A1H2 | { } | f1 | 2 | 720 | 5 | 5 | {5} | H4/H2A1 = 14400/10/2 = 720 | |
| A2A1 | {3} | f2 | 3 | 3 | 1200 | 2 | { } | H4/A2A1 = 14400/6/2 = 1200 | |
| A3 | {3,3} | f3 | 4 | 6 | 4 | 600 | ( ) | H4/A3 = 14400/24 = 600 |
Symmetries
The icosians are a specific set of Hamiltonian quaternions with the same symmetry as the 600-cell.[85] The icosians lie in the golden field, (a + b√5) + (c + d√5)i + (e + f√5)j + (g + h√5)k, where the eight variables are rational numbers.[86] The finite sums of the 120 unit icosians are called the icosian ring.
When interpreted as quaternions,[lower-alpha 5] the 120 vertices of the 600-cell form a group under quaternionic multiplication. This group is often called the binary icosahedral group and denoted by 2I as it is the double cover of the ordinary icosahedral group I.[88] It occurs twice in the rotational symmetry group RSG of the 600-cell as an invariant subgroup, namely as the subgroup 2IL of quaternion left-multiplications and as the subgroup 2IR of quaternion right-multiplications. Each rotational symmetry of the 600-cell is generated by specific elements of 2IL and 2IR; the pair of opposite elements generate the same element of RSG. The centre of RSG consists of the non-rotation Id and the central inversion −Id. We have the isomorphism RSG ≅ (2IL × 2IR) / {Id, -Id}. The order of RSG equals 120 × 120/2 = 7200. The quaternion algebra as a tool for the treatment of 3D and 4D rotations, and as a road to the full understanding of the theory of rotations in 4-dimensional Euclidean space, is described by Mebius.[89]
The binary icosahedral group is isomorphic to SL(2,5).
The full symmetry group of the 600-cell is the Weyl group of H4.[90] This is a group of order 14400. It consists of 7200 rotations and 7200 rotation-reflections. The rotations form an invariant subgroup of the full symmetry group. The rotational symmetry group was first described by S.L. van Oss.[91] The H4 group and its Clifford algebra construction from 3-dimensional symmetry groups by induction is described by Dechant.[92]
Visualization
The symmetries of the 3-D surface of the 600-cell are somewhat difficult to visualize due to both the large number of tetrahedral cells,[lower-alpha 27] and the fact that the tetrahedron has no opposing faces or vertices.[lower-alpha 53] One can start by realizing the 600-cell is the dual of the 120-cell. One may also notice that the 600-cell also contains the vertices of a dodecahedron,[41] which with some effort can be seen in most of the below perspective projections.
2D projections
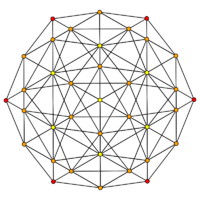
The H3 decagonal projection shows the plane of the van Oss polygon.
| H4 | - | F4 |
|---|---|---|
 [30] (Red=1) |
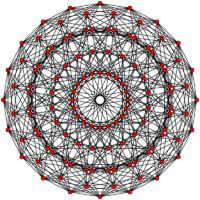 [20] (Red=1) |
 [12] (Red=1) |
| H3 | A2 / B3 / D4 | A3 / B2 |
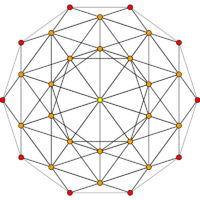 [10] (Red=1,orange=5,yellow=10) |
 [6] (Red=1,orange=3,yellow=6) |
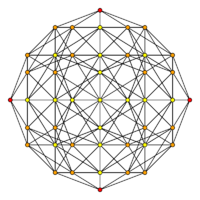 [4] (Red=1,orange=2,yellow=4) |
3D projections
A three-dimensional model of the 600-cell, in the collection of the Institut Henri Poincaré, was photographed in 1934–1935 by Man Ray, and formed part of two of his later "Shakesperean Equation" paintings.[93]
| Frame synchronized orthogonal isometric (left) and perspective (right) projections |
|---|
| File:Cell600Cmp.ogv |
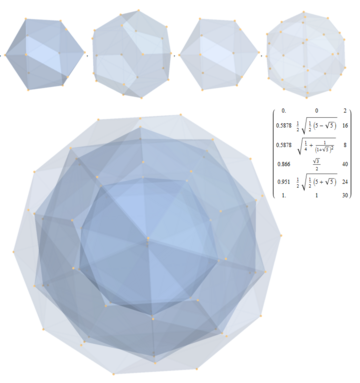
Diminished 600-cells
The snub 24-cell may be obtained from the 600-cell by removing the vertices of an inscribed 24-cell and taking the convex hull of the remaining vertices.[94] This process is a diminishing of the 600-cell.
The grand antiprism may be obtained by another diminishing of the 600-cell: removing 20 vertices that lie on two mutually orthogonal rings and taking the convex hull of the remaining vertices.[55]
A bi-24-diminished 600-cell, with all tridiminished icosahedron cells has 48 vertices removed, leaving 72 of 120 vertices of the 600-cell. The dual of a bi-24-diminished 600-cell, is a tri-24-diminished 600-cell, with 48 vertices and 72 hexahedron cells.
There are a total of 314,248,344 diminishings of the 600-cell by non-adjacent vertices. All of these consist of regular tetrahedral and icosahedral cells.[95]
| Diminished 600-cells | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Tri-24-diminished 600-cell | Bi-24-diminished 600-cell | Snub 24-cell (24-diminished 600-cell) |
Grand antiprism (20-diminished 600-cell) |
600-cell | ||||||
| Vertices | 48 | 72 | 96 | 100 | 120 | ||||||
| Vertex figure (Symmetry) |
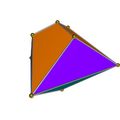 dual of tridiminished icosahedron ([3], order 6) |
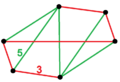 tetragonal antiwedge ([2]+, order 2) |
 tridiminished icosahedron ([3], order 6) |
 bidiminished icosahedron ([2], order 4) |
 Icosahedron ([5,3], order 120) | ||||||
| Symmetry | Order 144 (48×3 or 72×2) | [3+,4,3] Order 576 (96×6) |
10,2+,10 Order 400 (100×4) |
[5,3,3] Order 14400 (120×120) | |||||||
| Net | 
|

|
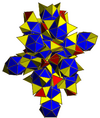
|
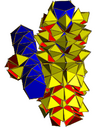
|

| ||||||
| Ortho H4 plane |
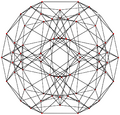
|

|
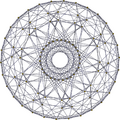
|
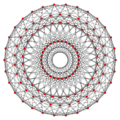
| |||||||
| Ortho F4 plane |

|

|
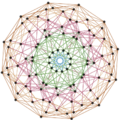
|

| |||||||
Related polytopes and honeycombs
The 600-cell is one of 15 regular and uniform polytopes with the same H4 symmetry [3,3,5]:[96]
It is similar to three regular 4-polytopes: the 5-cell {3,3,3}, 16-cell {3,3,4} of Euclidean 4-space, and the order-6 tetrahedral honeycomb {3,3,6} of hyperbolic space. All of these have tetrahedral cells.
This 4-polytope is a part of a sequence of 4-polytope and honeycombs with icosahedron vertex figures:
The regular complex polygons 3{5}3, ![]()
![]()
![]() and 5{3}5,
and 5{3}5, ![]()
![]()
![]() , in [math]\displaystyle{ \mathbb{C}^2 }[/math] have a real representation as 600-cell in 4-dimensional space. Both have 120 vertices, and 120 edges. The first has Complex reflection group 3[5]3, order 360, and the second has symmetry 5[3]5, order 600.[97]
, in [math]\displaystyle{ \mathbb{C}^2 }[/math] have a real representation as 600-cell in 4-dimensional space. Both have 120 vertices, and 120 edges. The first has Complex reflection group 3[5]3, order 360, and the second has symmetry 5[3]5, order 600.[97]
| Regular complex polytope in orthogonal projection of H4 Coxeter plane[14] | ||
|---|---|---|
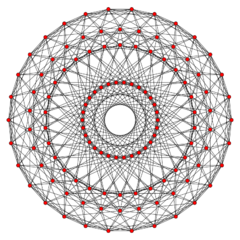 {3,3,5} Order 14400 |
 3{5}3 Order 360 |
 5{3}5 Order 600 |
See also
- 24-cell, the predecessor 4-polytope on which the 600-cell is based
- 120-cell, the dual 4-polytope to the 600-cell, and its successor
- Uniform 4-polytope family with [5,3,3] symmetry
- Regular 4-polytope
- Polytope
Notes
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 In the curved 3-dimensional space of the 600-cell's boundary surface, at each vertex one finds the twelve nearest other vertices surrounding the vertex the way an icosahedron's vertices surround its center. Twelve 600-cell edges converge at the icosahedron's center, where they appear to form six straight lines which cross there. However, the center is actually displaced in the 4th dimension (radially outward from the center of the 600-cell), out of the hyperplane defined by the icosahedron's vertices. Thus the vertex icosahedron is actually a canonical icosahedral pyramid,[lower-alpha 62] composed of 20 regular tetrahedra on a regular icosahedron base, and the vertex is its apex.[lower-alpha 63]
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 One might ask whether dimensional analogy "always works", or if it is perhaps "just guesswork" that might sometimes be incapable of producing a correct dimensionally analogous figure, especially when reasoning from a lower to a higher dimension. Apparently dimensional analogy in both directions has firm mathematical foundations. Dechant[38] derived the 4D symmetry groups from their 3D symmetry group counterparts by induction, demonstrating that there is nothing in 4D symmetry that is not already inherent in 3D symmetry. He showed that neither 4D symmetry nor 3D symmetry is more fundamental than the other, as either can be derived from the other. This is true whether dimensional analogies are computed using Coxeter group theory, or Clifford geometric algebra. These two rather different kinds of mathematics contribute complementary geometric insights.
- ↑ 3.0 3.1 3.2 The convex regular 4-polytopes can be ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. Each greater polytope in the sequence is rounder than its predecessor, enclosing more content[3] within the same radius. The 4-simplex (5-cell) is the limit smallest case, and the 120-cell is the largest. Complexity (as measured by comparing configuration matrices or simply the number of vertices) follows the same ordering. This provides an alternative numerical naming scheme for regular polytopes in which the 600-cell is the 120-point 4-polytope: fifth in the ascending sequence that runs from 5-point 4-polytope to 600-point 4-polytope.
- ↑ The edge length will always be different unless predecessor and successor are both radially equilateral, i.e. their edge length is the same as their radius (so both are preserved). Since radially equilateral polytopes are rare, the only such construction (in any dimension) is from the 8-cell to the 24-cell.
- ↑ 5.0 5.1 In four-dimensional Euclidean geometry, a quaternion is simply a (w, x, y, z) Cartesian coordinate. Hamilton did not see them as such when he discovered the quaternions. Schläfli would be the first to consider four-dimensional Euclidean space, publishing his discovery of the regular polyschemes in 1852, but Hamilton would never be influenced by that work, which remained obscure into the 20th century. Hamilton found the quaternions when he realized that a fourth dimension, in some sense, would be necessary in order to model rotations in three-dimensional space.[87] Although he described a quaternion as an ordered four-element multiple of real numbers, the quaternions were for him an extension of the complex numbers, not a Euclidean space of four dimensions.
- ↑ 6.0 6.1 6.2 thumb
- ↑ 7.0 7.1 7.2 7.3 7.4 7.5 A 24-cell contains 16 hexagons. In the 600-cell, with 25 24-cells, each 24-cell is disjoint from 8 24-cells and intersects each of the other 16 24-cells in six vertices that form a hexagon.[9] A 600-cell contains 25・16/2 = 200 such hexagons.
- ↑ In cases where inscribed 4-polytopes of the same kind occupy disjoint sets of vertices (such as the two 16-cells inscribed in the tesseract, or the three 16-cells inscribed in the 24-cell), their sets of vertex chords, central polygons and cells must likewise be disjoint. In the cases where they share vertices (such as the three tesseracts inscribed in the 24-cell, or the 25 24-cells inscribed in the 600-cell), they also share some vertex chords and central polygons.[lower-alpha 7]
- ↑ 9.0 9.1 9.2 9.3 9.4 The 600-cell contains exactly 25 24-cells, 75 16-cells and 75 8-cells, with each 16-cell and each 8-cell lying in just one 24-cell.[18]
- ↑ 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 Polytopes are completely disjoint if all their element sets are disjoint: they do not share any vertices, edges, faces or cells. They may still overlap in space, sharing 4-content, volume, area, or lineage.
- ↑ Each of the 25 24-cells of the 600-cell contains exactly one vertex of each great pentagon.[9] Six pentagons intersect at each 600-cell vertex, so each 24-cell intersects all 144 great pentagons.
- ↑ 12.0 12.1 12.2 12.3 12.4 12.5 Five 24-cells meet at each icosahedral pyramid apex[lower-alpha 1] of the 600-cell. Each 24-cell shares not just one vertex but 6 vertices (one of its four hexagonal central planes) with each of the other four 24-cells.[lower-alpha 7]
- ↑ 13.0 13.1 13.2 Schoute was the first to state (a century ago) that there are exactly ten ways to partition the 120 vertices of the 600-cell into five disjoint 24-cells. The 25 24-cells can be placed in a 5 x 5 array such that each row and each column of the array partitions the 120 vertices of the 600-cell into five disjoint 24-cells. The rows and columns of the array are the only ten such partitions of the 600-cell.[18]
- ↑ 14.0 14.1 14.2 14.3 14.4 The 600-cell contains 25 distinct 24-cells, bound to each other by pentagonal rings. Each pentagon links five completely disjoint[lower-alpha 10] 24-cells together, the collective vertices of which are the 120 vertices of the 600-cell. Each 24-point 24-cell contains one fifth of all the vertices in the 120-point 600-cell, and is linked to the other 96 vertices (which comprise a snub 24-cell) by the 600-cell's 144 pentagons. Each of the 25 24-cells intersects each of the 144 great pentagons at just one vertex.[lower-alpha 11] Five 24-cells meet at each 600-cell vertex,[lower-alpha 12] so all 25 24-cells are linked by each great pentagon. The 600-cell can be partitioned into five disjoint 24-cells (10 different ways),[lower-alpha 13] and also into 24 disjoint pentagons (inscribed in the 12 Clifford parallel great decagons of one of the 6 decagonal fibrations) by choosing a pentagon from the same fibration at each 24-cell vertex.
- ↑ 15.0 15.1 In 4 dimensional space we can construct 4 perpendicular axes and 6 perpendicular planes through a point. Without loss of generality, we may take these to be the axes and orthogonal central planes of a (w, x, y, z) Cartesian coordinate system. In 4 dimensions we have the same 3 orthogonal planes (xy, xz, yz) that we have in 3 dimensions, and also 3 others (wx, wy, wz). Each of the 6 orthogonal planes shares an axis with 4 of the others, and is completely orthogonal to just one of the others: the only one with which it does not share an axis. Thus there are 3 pairs of completely orthogonal planes: xy and wz intersect only at the origin; xz and wy intersect only at the origin; yz and wx intersect only at the origin.
- ↑ 16.0 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 Two flat planes A and B of a Euclidean space of four dimensions are called completely orthogonal if and only if every line in A is orthogonal to every line in B. In that case the planes A and B intersect at a single point O, so that if a line in A intersects with a line in B, they intersect at O. A and B are perpendicular and Clifford parallel.[lower-alpha 15]
- ↑ The angles 𝜉i and 𝜉j are angles of rotation in the two completely orthogonal[lower-alpha 16] invariant planes which characterize rotations in 4-dimensional Euclidean space. The angle 𝜂 is the inclination of both these planes from the polar axis, where 𝜂 ranges from 0 to 𝜋/2. The (𝜉i, 0, 𝜉j) coordinates describe the great circles which intersect at the north and south pole ("lines of longitude"). The (𝜉i, 𝜋/2, 𝜉j) coordinates describe the great circles orthogonal to longitude ("equators"); there is more than one "equator" great circle in a 4-polytope, as the equator of a 3-sphere is a whole 2-sphere of great circles. The other Hopf coordinates (𝜉i, 0 < 𝜂 < 𝜋/2, 𝜉j) describe the great circles (not "lines of latitude") which cross an equator but do not pass through the north or south pole.
- ↑ The conversion from Hopf coordinates (𝜉i, 𝜂, 𝜉j) to unit-radius Cartesian coordinates (w, x, y, z) is:
- w = cos 𝜉i sin 𝜂
- x = cos 𝜉j cos 𝜂
- y = sin 𝜉j cos 𝜂
- z = sin 𝜉i sin 𝜂
- ↑ The Hopf coordinates[10] are triples of three angles:
- (𝜉i, 𝜂, 𝜉j)
- ↑ There are 600 permutations of these coordinates, but there are only 120 vertices in the 600-cell. These are actually the Hopf coordinates of the vertices of the 120-cell, which has 600 vertices and can be seen (two different ways) as a compound of 5 disjoint 600-cells.
- ↑ 21.0 21.1 21.2 The fractional-root golden chords are irrational fractions that are functions of √5. They exemplify that the golden ratio φ = 1 + √5/2 ≈ 1.618 is a circle ratio related to 𝜋:[17]
- 𝜋/5 = arccos (φ/2)
- φ = 1 – 2 cos (3𝜋/5)
- ↑ 22.0 22.1 The 600-cell edges are decagon edges of length √0.𝚫, which is 𝚽, the smaller golden section of √5; the edges are in the inverse golden ratio 1/φ to the √1 hexagon chords (the 24-cell edges). The other fractional-root chords exhibit golden relationships as well. The chord of length √1.𝚫 is a pentagon edge. The next fractional-root chord is a decagon diagonal of length √2.𝚽 which is φ, the larger golden section of √5; it is in the golden ratio[lower-alpha 21] to the √1 chord (and the radius).[lower-alpha 25] The last fractional-root chord is the pentagon diagonal of length √3.𝚽. The diagonal of a regular pentagon is always in the golden ratio to its edge, and indeed φ√1.𝚫 is √3.𝚽.
- ↑ 23.0 23.1 23.2 23.3 23.4 23.5 The long radius (center to vertex) of the 600-cell is in the golden ratio to its edge length; thus its radius is φ if its edge length is 1, and its edge length is 1/φ if its radius is 1. Only a few uniform polytopes have this property, including the four-dimensional 600-cell, the three-dimensional icosidodecahedron, and the two-dimensional decagon. (The icosidodecahedron is the equatorial cross section of the 600-cell, and the decagon is the equatorial cross section of the icosidodecahedron.) Radially golden polytopes are those which can be constructed, with their radii, from golden triangles[lower-alpha 28] which meet at the center, each contributing two radii and an edge.
- ↑ The fractional square roots are given as decimal fractions where:
𝚽 ≈ 0.618 is the inverse golden ratio [math]\displaystyle{ \tfrac{1}{\phi} = \phi^{-1} }[/math]
𝚫 = 1 - 𝚽 = 𝚽2 ≈ 0.382
For example:
𝚽 = √0.𝚫 = √0.382~ ≈ 0.618 - ↑ Notice in the diagram how the φ chord (the larger golden section) sums with the adjacent 𝚽 edge (the smaller golden section) to √5, as if together they were a √5 chord bent to fit inside the √4 diameter.
- ↑ 26.0 26.1 Consider one of the 24-vertex 24-cells inscribed in the 120-vertex 600-cell. The other 96 vertices constitute a snub 24-cell. Removing any one 24-cell from the 600-cell produces a snub 24-cell.
- ↑ 27.0 27.1 27.2 Each tetrahedral cell touches, in some manner, 56 other cells. One cell contacts each of the four faces; two cells contact each of the six edges, but not a face; and ten cells contact each of the four vertices, but not a face or edge.
- ↑ 28.0 28.1 28.2 A golden triangle is an isosceles triangle in which the duplicated side a is in the golden ratio to the distinct side b:
- a/b = φ = 1 + √5/2 ≈ 1.618
The vertex angle is:- 𝛉 = arccos(φ/2) = 𝜋/5 = 36°
- ↑ 29.0 29.1 Beginning with the 16-cell, every regular convex 4-polytope in the unit-radius sequence is inscribed in its successor.[5] Therefore the successor may be constructed by placing 4-pyramids of some kind on the cells of its predecessor. Between the 16-cell and the tesseract, we have 16 right tetrahedral pyramids, with their apexes filling the corners of the tesseract. Between the tesseract and the 24-cell, we have 8 canonical cubic pyramids. But if we place 24 canonical octahedral pyramids on the 24-cell, we only get another tesseract (of twice the radius and edge length), not the successor 600-cell. Between the 24-cell and the 600-cell there must be 24 smaller, irregular 4-pyramids on a regular octahedral base.
- ↑ 30.0 30.1 30.2 30.3 30.4 The six great decagons which pass by each tetrahedral cell along its edges do not all intersect with each other, because the 6 edges of the tetrahedron do not all share a vertex. Each decagon intersects four of the others (at 60 degrees), but just misses one of the others as they run past each other (at 90 degrees) along the opposite and perpendicular skew edges of the tetrahedron. Each tetrahedron links three pairs of decagons which do not intersect at a vertex of the tetrahedron. However, none of the six decagons are Clifford parallel;[lower-alpha 33] each belongs to a different Hopf fiber bundle of 12. Only one of the tetrahedron's six edges may be part of a helix in any one Boerdijk–Coxeter triple helix ring.[lower-alpha 31] Incidentally, this footnote is one of a tetrahedron of four footnotes about Clifford parallel decagons[lower-alpha 32] that all reference each other.
- ↑ 31.00 31.01 31.02 31.03 31.04 31.05 31.06 31.07 31.08 31.09 31.10 Since tetrahedra[lower-alpha 30] do not have opposing faces, the only way they can be stacked face-to-face in a straight line is in the form of a twisted chain called a Boerdijk-Coxeter helix. This is a Clifford parallel[lower-alpha 33] triple helix as shown in the illustration. In the 600-cell we find them bent in the fourth dimension into geodesic rings. Each ring has 30 cells and touches 30 vertices. The cells are each face-bonded to two adjacent cells, but one of the six edges of each tetrahedron belongs only to that cell, and these 30 edges form 3 Clifford parallel great decagons which spiral around each other.[lower-alpha 32] 5 30-cell rings meet at and spiral around each decagon (as 5 tetrahedra meet at each edge). A bundle of 20 such cell-disjoint rings fills the entire 600-cell, thus constituting a discrete Hopf fibration. There are 6 distinct such Hopf fibrations, covering the same space but running in different "directions".
- ↑ 32.0 32.1 32.2 32.3 32.4 32.5 32.6 Two Clifford parallel[lower-alpha 33] great decagons don't intersect, but their corresponding vertices are linked by one edge of another decagon. The two parallel decagons and the ten linking edges form a double helix ring. Three decagons can also be parallel (decagons come in parallel fiber bundles of 12) and three of them may form a triple helix ring. If the ring is cut and laid out flat in 3-space, it is a Boerdijk–Coxeter helix[lower-alpha 31] 30 tetrahedra[lower-alpha 30] long. The three Clifford parallel decagons can be seen as the cyan edges in the triple helix illustration. Each magenta edge is one edge of another decagon linking two parallel decagons.
- ↑ 33.00 33.01 33.02 33.03 33.04 33.05 33.06 33.07 33.08 33.09 33.10 33.11 33.12 33.13 33.14 33.15 Clifford parallels are non-intersecting curved lines that are parallel in the sense that the perpendicular (shortest) distance between them is the same at each point. A double helix is an example of Clifford parallelism in ordinary 3-dimensional Euclidean space. In 4-space Clifford parallels occur as geodesic great circles on the 3-sphere.[20] Whereas in 3-dimensional space, any two geodesic great circles on the 2-sphere will always intersect at two antipodal points, in 4-dimensional space not all great circles intersect; various sets of Clifford parallel non-intersecting geodesic great circles can be found on the 3-sphere. They spiral around each other in Hopf fiber bundles which, in the 600-cell, visit all 120 vertices just once. For example, each of the 600 tetrahedra participates in 6 great decagons[lower-alpha 30] belonging to 6 discrete Hopf fibrations, each filling the whole 600-cell. Each fibration is a bundle of 12 Clifford parallel decagons which form 20 cell-disjoint intertwining rings of 30 tetrahedral cells,[lower-alpha 31] each bounded by three of the 12 great decagons.[lower-alpha 32]
- ↑ The 10 hexagons which cross at each vertex lie along the 20 short radii of the icosahedral vertex figure.[lower-alpha 1]
- ↑ 35.0 35.1 The 25 inscribed 24-cells each have 3 inscribed tesseracts, which each have 8 √1 cubic cells. The 1200 √3 chords are the 4 long diameters of these 600 cubes. The three tesseracts in each 24-cell overlap, and each √3 chord is a long diameter of two different cubes, in two of the three tesseracts. Each cube belongs to just one tesseract in just one 24-cell.
- ↑ The sum of 0.𝚫・720 + 1・1200 + 1.𝚫・720 + 2・1800 + 2.𝚽・720 + 3・1200 + 3.𝚽・720 + 4・60 is 14,400.
- ↑ The sum of the squared lengths of all the distinct chords of any regular convex n-polytope of unit radius is the square of the number of vertices.[25]
- ↑ A triacontagon or 30-gon is a thirty-sided polygon. The triacontagon is the largest regular polygon whose interior angle is the sum of the interior angles of smaller polygons: 168° is the sum of the interior angles of the equilateral triangle (60°) and the regular pentagon (108°).
- ↑ 39.0 39.1 39.2 The 600-cell has 72 great 30-gons: 6 sets of 12 Clifford parallel 30-gon central planes, each completely orthogonal to a decagon central plane. Unlike the great circles of the unit-radius 600-cell that pass through its vertices, this 30-gon is not actually a great circle of the unit-radius 3-sphere. Because it passes through face centers rather than vertices, it has a shorter radius and lies on a smaller 3-sphere. Of course, there is also a unit-radius great circle in this central plane completely orthogonal to a decagon central plane, but as a great circle polygon it is a 0-gon, not a 30-gon, because it intersects none of the points of the 600-cell. In the 600-cell, the great circle polygon completely orthogonal to each great decagon is a 0-gon.
- ↑ 40.0 40.1 The 30 vertices and 30 edges of the 30-cell ring lie on a skew {30/11} star polygon with a winding number of 11 called a triacontagram11, a continuous tight corkscrew helix bent into a loop of 30 edges (the magenta edges in the triple helix illustration), which winds 11 times around itself in the course of a single revolution around the 600-cell, accompanied by a single 360 degree twist of the 30-cell ring.[31] The same 30-cell ring can also be characterized as the Petrie polygon of the 600-cell.[lower-alpha 81]
- ↑ 41.0 41.1 41.2 41.3 41.4 41.5 Each great decagon central plane is completely orthogonal[lower-alpha 16] to a great 30-gon[lower-alpha 38] central plane which does not intersect any vertices of the 600-cell. The 72 30-gons are each the center axis of a 30-cell Boerdijk–Coxeter triple helix ring,[lower-alpha 31] with each segment of the 30-gon passing through a tetrahedron similarly. The 30-gon great circle resides completely in the curved 3-dimensional surface of its 3-sphere;[lower-alpha 39] its curved segments are not chords. It does not touch any edges or vertices, but it does hit faces. It is the central axis of a spiral skew 30-gram, the Petrie polygon of the 600-cell which links all 30 vertices of the 30-cell Boerdijk–Coxeter helix, with three of its edges in each cell.[lower-alpha 40]
- ↑ 42.00 42.01 42.02 42.03 42.04 42.05 42.06 42.07 42.08 42.09 42.10 42.11 42.12 42.13 42.14 A point under isoclinic rotation traverses the diagonal[lower-alpha 96] straight line of a single isoclinic geodesic, reaching its destination directly, instead of the bent line of two successive simple geodesics. A geodesic is the shortest path through a space (intuitively, a string pulled taught between two points). Simple geodesics are great circles lying in a central plane (the only kind of geodesics that occur in 3-space on the 2-sphere). Isoclinic geodesics are different: they do not lie in a single plane; they are 4-dimensional spirals rather than simple 2-dimensional circles.[lower-alpha 58] But they are not like 3-dimensional screw threads either, because they form a closed loop like any circle.[lower-alpha 97] Isoclinic geodesics are 4-dimensional great circles, and they are just as circular as 2-dimensional circles: in fact, twice as circular, because they curve in a circle in two completely orthogonal directions at once.[lower-alpha 83] They are true circles,[lower-alpha 91] and even form fibrations like ordinary 2-dimensional great circles. These isoclines are geodesic 1-dimensional lines embedded in a 4-dimensional space. On the 3-sphere[lower-alpha 98] they always occur in chiral pairs as Villarceau circles on the Clifford torus,[lower-alpha 101] the geodesic paths traversed by vertices in an isoclinic rotation. They are helices bent into a Möbius loop in the fourth dimension, taking a diagonal winding route around the 3-sphere through the non-adjacent vertices of a 4-polytope's skew Clifford polygon.[lower-alpha 100]
- ↑ 43.0 43.1 43.2 43.3 43.4 In 4-space no more than 4 great circles may be Clifford parallel[lower-alpha 33] and all the same angular distance apart.[27] Such central planes are mutually isoclinic: each pair of planes is separated by two equal angles, and an isoclinic rotation by that angle will bring them together. Where three or four such planes are all separated by the same angle, they are called equi-isoclinic.
- ↑ 44.0 44.1 44.2 The decagonal planes in the 600-cell occur in equi-isoclinic[lower-alpha 43] groups of 3, everywhere 3 Clifford parallel decagons 36° (𝝅/5) apart form a 30-cell Boerdijk–Coxeter triple helix ring.[lower-alpha 31] Also Clifford parallel to those 3 decagons are 3 equi-isoclinic decagons 72° (2𝝅/5) apart, 3 108° (3𝝅/5) apart, and 3 144° (4𝝅/5) apart, for a total of 12 Clifford parallel decagons (120 vertices) that comprise a discrete Hopf fibration. Because the great decagons lie in isoclinic planes separated by two equal angles, their corresponding vertices are separated by a combined vector relative to both angles. Vectors in 4-space may be combined by quaternionic multiplication, discovered by Hamilton.[28] The corresponding vertices of two great polygons which are 36° (𝝅/5) apart by isoclinic rotation are 60° (𝝅/3) apart in 4-space. The corresponding vertices of two great polygons which are 108° (3𝝅/5) apart by isoclinic rotation are also 60° (𝝅/3) apart in 4-space. The corresponding vertices of two great polygons which are 72° (2𝝅/5) apart by isoclinic rotation are 120° (2𝝅/3) apart in 4-space, and the corresponding vertices of two great polygons which are 144° (4𝝅/5) apart by isoclinic rotation are also 120° (2𝝅/3) apart in 4-space.
- ↑ 45.0 45.1 45.2 The hexagonal planes in the 600-cell occur in equi-isoclinic[lower-alpha 43] groups of 4, everywhere 4 Clifford parallel hexagons 60° (𝝅/3) apart form a 24-cell. Also Clifford parallel to those 4 hexagons are 4 equi-isoclinic hexagons 36° (𝝅/5) apart, 4 72° (2𝝅/5) apart, 4 108° (3𝝅/5) apart, and 4 144° (4𝝅/5) apart, for a total of 20 Clifford parallel hexagons (120 vertices) that comprise a discrete Hopf fibration.
- ↑ 46.0 46.1 46.2 The square planes in the 600-cell occur in equi-isoclinic[lower-alpha 43] groups of 2, everywhere 2 Clifford parallel squares 90° (𝝅/2) apart form a 16-cell. Also Clifford parallel to those 2 squares are 4 equi-isoclinic groups of 4, where 3 Clifford parallel 16-cells 60° (𝝅/3) apart form a 24-cell. Also Clifford parallel are 4 equi-isoclinic groups of 3: 3 36° (𝝅/5) apart, 3 72° (2𝝅/5) apart, 3 108° (3𝝅/5) apart, and 3 144° (4𝝅/5) apart, for a total of 30 Clifford parallel squares (120 vertices) that comprise a discrete Hopf fibration.
- ↑ 47.0 47.1 47.2 47.3 47.4 Two angles are required to fix the relative positions of two planes in 4-space.[26] Since all planes in the same hyperplane are 0 degrees apart in one of the two angles, only one angle is required in 3-space. Great decagons are a multiple (from 0 to 4) of 36° (𝝅/5) apart in each angle, and may be the same angle apart in both angles.[lower-alpha 44] Great hexagons may be 60° (𝝅/3) apart in one or both angles, and may be a multiple (from 0 to 4) of 36° (𝝅/5) apart in one or both angles.[lower-alpha 45] Great squares may be 90° (𝝅/2) apart in one or both angles, may be 60° (𝝅/3) apart in one or both angles, and may be a multiple (from 0 to 4) of 36° (𝝅/5) apart in one or both angles.[lower-alpha 46] Planes which are separated by two equal angles are called isoclinic.[lower-alpha 43] Planes which are isoclinic have Clifford parallel great circles.[lower-alpha 33] A great hexagon and a great decagon may be isoclinic, but more often they are separated by a 𝝅/3 (60°) angle and a multiple (from 1 to 4) of 𝝅/5 (36°) angle.
- ↑ 48.0 48.1 48.2 48.3 In the 24-cell each great square plane is completely orthogonal[lower-alpha 16] to another great square plane, and each great hexagon plane is completely orthogonal to a plane which intersects only two antipodal vertices: a great digon plane.
- ↑ 49.0 49.1 49.2 49.3 49.4 49.5 Each Hopf fibration of the 3-sphere into Clifford parallel great circle fibers has a map (called its base) which is an ordinary 2-sphere.[39] On this map each great circle fiber appears as a single point. The base of a great decagon fibration of the 600-cell is the icosahedron, in which each vertex represents one of the 12 great decagons.[21] To a toplogist the base is not necessarily any part of the thing it maps: the base icosahedron is not expected to be a cell or interior feature of the 600-cell, it is merely the dimensionally analogous sphere,[lower-alpha 2] useful for reasoning about the fibration. But in fact the 600-cell does have icosahedra in it: 120 icosahedral vertex figures,[lower-alpha 1] any of which can be seen as its base: a 3-dimensional 1:10 scale model of the whole 4-dimensional 600-cell. Each 3-dimensional vertex icosahedron is lifted to the 4-dimensional 600-cell by a 720 degree isoclinic rotation,[lower-alpha 42] which takes each of its 4 disjoint triangular faces in a circuit around one of 4 disjoint 30-vertex rings of 30 tetrahedral cells (each braided of 3 Clifford parallel great decagons), and so visits all 120 vertices of the 600-cell. Since the 12 decagonal great circles (of the 4 rings) are Clifford parallel decagons of the same fibration, we can see geometrically how the icosahedron works as a map of a Hopf fibration of the entire 600-cell, and how the Hopf fibration is an expression of an isoclinic symmetry.[40]
- ↑ 50.0 50.1 The regular skew 30-gon is the Petrie polygon of the 600-cell and its dual the 120-cell. The Petrie polygons of the 120-cell occur in the 600-cell as duals of the 30-cell Boerdijk–Coxeter helix rings: connecting their 30 cell centers together produces the Petrie polygons of the dual 120-cell, as noticed by Rolfdieter Frank (circa 2001). Thus he discovered that the vertex set of the 120-cell partitions into 20 non-intersecting Petrie polygons. This set of 20 disjoint Clifford parallel skew polygons is a discrete Hopf fibration of the 120-cell (just as their 20 dual 30-cell rings are a discrete fibration of the 600-cell).
- ↑ 51.0 51.1 51.2 These are the √2 tetrahedral cells of the 75 inscribed 16-cells, not the √0.𝚫 tetrahedral cells of the 600-cell.
- ↑ 52.0 52.1 ‟The Petrie polygons of the Platonic solid [math]\displaystyle{ \{p, q\} }[/math] correspond to equatorial polygons of the truncation [math]\displaystyle{ \{\tfrac{p}{q}\} }[/math] and to equators of the simplicially subdivided spherical tessellation [math]\displaystyle{ \{p, q\} }[/math]. This "simplicial subdivision" is the arrangement of [math]\displaystyle{ g = g_{p, q} }[/math] right-angled spherical triangles into which the sphere is decomposed by the planes of symmetry of the solid. The great circles that lie in these planes were formerly called "lines of symmetry", but perhaps a more vivid name is reflecting circles. The analogous simplicial subdivision of the spherical honeycomb [math]\displaystyle{ \{p, q, r\} }[/math] consists of the [math]\displaystyle{ g = g_{p, q, r} }[/math] tetrahedra 0123 into which a hypersphere (in Euclidean 4-space) is decomposed by the hyperplanes of symmetry of the polytope [math]\displaystyle{ \{p, q, r\} }[/math]. The great spheres which lie in these hyperplanes are naturally called reflecting spheres. Since the orthoscheme has no obtuse angles, it entirely contains the arc that measures the absolutely shortest distance 𝝅/h [between the] 2h tetrahedra [that] are strung like beads on a necklace, or like a "rotating ring of tetrahedra" ... whose opposite edges are generators of a helicoid. The two opposite edges of each tetrahedron are related by a screw-displacement.[lower-alpha 67] Hence the total number of spheres is 2h.”[62]
- ↑ 53.0 53.1 53.2 The fibration's Clifford parallel cell rings may or may not be chiral objects, depending upon whether the 4-polytope's cells have opposing faces or not. The characteristic cell rings of the 16-cell and 600-cell (with tetrahedral cells) are chiral: they twist either clockwise or counterclockwise. Isoclines acting with either left or right chirality (not both) run through cell rings of this kind, though each fibration contains both left and right cell rings.[lower-alpha 116] The characteristic cell rings of the tesseract, 24-cell and 120-cell (with cubical, octahedral, and dodecahedral cells respectively) are directly congruent, not chiral: there is only one kind of characteristic cell ring in each of these 4-polytopes, and it is not twisted (it has no torsion). Pairs of left-handed and right-handed isoclines run through cell rings of this kind. Note that all these 4-polytopes (except the 16-cell) contain fibrations of their inscribed predecessors' characteristic cell rings in addition to their own characteristic fibrations, so the 600-cell contains both chiral and directly congruent cell rings.
- ↑ 54.0 54.1 The choice of a partitioning of a regular 4-polytope into cell rings is arbitrary, because all of its cells are identical. No particular fibration is distinguished, unless the 4-polytope is rotating. In isoclinic rotations, one set of cell rings (one fibration) is distinguished as the unique container of that distinct left-right pair of rotations and its isoclines.
- ↑ 55.0 55.1 The only way to partition the 120 vertices of the 600-cell into 4 completely disjoint 30-vertex, 30-cell rings[lower-alpha 31] is by partitioning each of 15 completely disjoint 16-cells similarly into 4 symmetric parts: 4 antipodal vertex pairs lying on the 4 orthogonal axes of the 16-cell. The 600-cell contains 75 distinct 16-cells which can be partitioned into sets of 15 completely disjoint 16-cells. In any set of 4 completely disjoint 30-cell rings, there is a set of 15 completely disjoint 16-cells, with one axis of each 16-cell in each 30-cell ring.
- ↑ Unlike their bounding decagons, the 20 cell rings themselves are not all Clifford parallel to each other, because only completely disjoint polytopes are Clifford parallel.[lower-alpha 10] The 20 cell rings have 5 different subsets of 4 Clifford parallel cell rings. Each cell ring is bounded by 3 Clifford parallel great decagons, so each subset of 4 Clifford parallel cell rings is bounded by a total of 12 Clifford parallel great decagons (a discrete Hopf fibration). In fact each of the 5 different subsets of 4 cell rings is bounded by the same 12 Clifford parallel great decagons (the same Hopf fibration); there are 5 different ways to see the same 12 decagons as a set of 4 cell rings (and equivalently, just one way to see them as a single set of 20 cell rings).
- ↑ Note that the differently colored helices of cells are different cell rings (or ring-shaped holes) in the same fibration, not the different fibrations of the 4-polytope. Each fibration is the entire 4-polytope.
- ↑ 58.0 58.1 58.2 58.3 58.4 58.5 In a double rotation each vertex can be said to move along two completely orthogonal great circles at the same time, but it does not stay within the central plane of either of those original great circles; rather, it moves along a helical geodesic that traverses diagonally between great circles. The two completely orthogonal planes of rotation are said to be invariant because the points in each stay in their places in the plane as the plane moves, rotating and tilting sideways by the angle that the other plane rotates.
- ↑ 59.0 59.1 59.2 The poles of the invariant axis of a rotating 2-sphere are dimensionally analogous to the pair of invariant planes of a rotating 3-sphere. The poles of the rotating 2-sphere are dimensionally analogous to linked great circles on the 3-sphere. By dimensional analogy, each 1D point in 3D lifts to a 2D line in 4D, in this case a circle.[lower-alpha 49] The two antipodal rotation poles lift to a pair of circular Hopf fibers which are not merely Clifford parallel and interlinked,[lower-alpha 33] but also completely orthogonal.[lower-alpha 16] The invariant great circles of the 4D rotation are its poles. In the case of an isoclinic rotation, there is not merely one such pair of 2D poles (completely orthogonal Hopf great circle fibers), there are many such pairs: a finite number of circle-pairs if the 3-sphere fibration is discrete (e.g. a regular polytope with a finite number of vertices), or else an infinite number of orthogonal circle-pairs, entirely filling the 3-sphere. Every point in the curved 3-space of the 3-sphere lies on one such circle (never on two, since the completely orthogonal circles, like all the Clifford parallel Hopf great circle fibers, do not intersect). Where a 2D rotation has one pole, and a 3D rotation of a 2-sphere has 2 poles, an isoclinic 4D rotation of a 3-sphere has nothing but poles, an infinite number of them. In a discrete 4-polytope, all the Clifford parallel invariant great polygons of the rotation are poles, and they fill the 4-polytope, passing through every vertex just once. In one full revolution of such a rotation, every point in the space loops exactly once through its pole-circle.[lower-alpha 115] The circles are arranged with a surprising symmetry, so that each pole-circle links with every other pole-circle, like a maximally dense fabric of 4D chain mail in which all the circles are linked through each other, but no two circles ever intersect.
- ↑ The 4 red faces of the snub tetrahedron correspond to the 4 completely disjoint cell rings of the sparse construction of the fibration (its subfibration). The red faces are centered on the vertices of an inscribed tetrahedron, and lie in the center of the larger faces of an inscribing tetrahedron.
- ↑ 61.0 61.1 Because the octahedron can be snub truncated yielding an icosahedron,[45] another name for the icosahedron is snub octahedron. This term refers specifically to a lower symmetry arrangement of the icosahedron's faces (with 8 faces of one color and 12 of another).
- ↑ 62.0 62.1 62.2 The 120-point 600-cell has 120 overlapping icosahedral pyramids.[lower-alpha 1]
- ↑ The icosahedron is not radially equilateral in Euclidean 3-space, but an icosahedral pyramid is radially equilateral in the curved 3-space of the 600-cell's surface (the 3-sphere). In 4-space the 12 edges radiating from its apex are not actually its radii: the apex of the icosahedral pyramid is not actually its center, just one of its vertices. But in curved 3-space the edges radiating symmetrically from the apex are radii, so the icosahedron is radially equilateral in that curved 3-space. In Euclidean 4-space 24 edges radiating symmetrically from a central point make the radially equilateral 24-cell, and a symmetrical subset of 16 of those edges make the radially equilateral tesseract.
- ↑ An icosahedron edge between two blue faces is surrounded by two blue-faced icosahedral pyramid cells and 3 cells from an adjacent cluster of 5 cells (one of which is the central tetrahedron of the five)
- ↑ The pentagonal pyramids around each vertex of the "snub octahedron" icosahedron all look the same, with two yellow and three blue faces. Each pentagon has five distinct rotational orientations. Rotating any pentagonal pyramid rotates all of them, so the five rotational positions are the only five different ways to arrange the colors.
- ↑ Notice that the contraction is chiral, since there are two choices of diagonal on which to begin folding the square faces.
- ↑ 67.0 67.1 67.2 Let Q denote a rotation, R a reflection, T a translation, and let Qq Rr T denote a product of several such transformations, all commutative with one another. Then RT is a glide-reflection (in two or three dimensions), QR is a rotary-reflection, QT is a screw-displacement, and Q2 is a double rotation (in four dimensions). Every orthogonal transformation is expressible as
Qq Rr
where 2q + r ≤ n, the number of dimensions. Transformations involving a translation are expressible as
Qq Rr T
where 2q + r + 1 ≤ n.
For n = 4 in particular, every displacement is either a double rotation Q2, or a screw-displacement QT (where the rotation component Q is a simple rotation). [If we assume the Galilean principle of relativity, every displacement in 4-space can be viewed as either of those, because we can view any QT as a Q2 in a linearly moving (translating) reference frame. Therefore any transformation from one inertial reference frame to another is expressable as a Q2. By the same principle, we can view any QT or Q2 as an isoclinic (equi-angled) Q2 by appropriate choice of reference frame.[lower-alpha 93] That is to say, Coxeter's relation is a mathematical statement of the principle of relativity, on group-theoretic grounds.] Every enantiomorphous transformation in 4-space (reversing chirality) is a QRT.[65] - ↑ There is a vertex icosahedron[lower-alpha 1] inside each 24-cell octahedral central section (not inside a √1 octahedral cell, but in the larger √2 octahedron that lies in a central hyperplane), and a larger icosahedron inside each 24-cell cuboctahedron. The two different-sized icosahedra are the second and fourth sections of the 600-cell (beginning with a vertex). The octahedron and the cuboctahedron are the central sections of the 24-cell (beginning with a vertex and beginning with a cell, respectively).[47] The cuboctahedron, large icosahedron, octahedron, and small icosahedron nest like Russian dolls and are related by a helical contraction.[48] The contraction begins with the square faces of the cuboctahedron folding inward along their diagonals to form pairs of triangles.[lower-alpha 66] The 12 vertices of the cuboctahedron move toward each other to the points where they form a regular icosahedron (the large icosahedron); they move slightly closer together until they form a Jessen's icosahedron; they continue to spiral toward each other until they merge into the 8 vertices of the octahedron;[49] and they continue moving along the same helical paths, separating again into the 12 vertices of the snub octahedron (the small icosahedron).[lower-alpha 61] The geometry of this sequence of transformations[lower-alpha 67] in S3 is similar to the kinematics of the cuboctahedron and the tensegrity icosahedron in R3. The twisting, expansive-contractive transformations between these polyhedra were named Jitterbug transformations by Buckminster Fuller.[50]
- ↑ These 12 cells are edge-bonded to the central cell, face-bonded to the exterior faces of the cluster of 5, and face-bonded to each other in pairs. They are blue-faced cells in the 6 different icosahedral pyramids surrounding the cluster of 5.
- ↑ The √1 tetrahedron has a volume of 9 √0.𝚫 tetrahedral cells. In the curved 3-dimensional volume of the 600 cells, it encloses the cluster of 5 cells, which do not entirely fill it. The 6 dipyramids (12 cells) which fit into the concavities of the cluster of 5 cells overfill it: only one third of each dipyramid lies within the √1 tetrahedron. The dipyramids contribute one-third of each of 12 cells to it, a volume equivalent to 4 cells.
- ↑ The 600-cell also contains 600 octahedra. The first section of the 600-cell beginning with a cell is tetrahedral, and the third section is octahedral. These internal octahedra are not cells of the 600-cell because they are not volumetrically disjoint, but they are each a cell of one of the 25 internal 24-cells. The 600-cell also contains 600 cubes, each a cell of one of its 75 internal 8-cell tesseracts.[lower-alpha 35]
- ↑ Each √1 edge of the octahedral cell is the long diameter of another tetrahedral dipyramid (two more face-bonded tetrahedral cells). In the 24-cell, three octahedral cells surround each edge, so one third of the dipyramid lies inside each octahedron, split between two adjacent concave faces. Each concave face is filled by one-sixth of each of the three dipyramids that surround its three edges, so it has the same volume as one tetrahedral cell.
- ↑ A √1 octahedral cell (of any 24-cell inscribed in the 600-cell) has six vertices which all lie in the same hyperplane: they bound an octahedral section (a flat three-dimensional slice) of the 600-cell. The same √1 octahedron filled by 25 tetrahedral cells has a total of 14 vertices lying in three parallel three-dimensional sections of the 600-cell: the 6-point √1 octahedral section, a 4-point √1 tetrahedral section, and a 4-point √0.𝚫 tetrahedral section. In the curved three-dimensional space of the 600-cell's surface, the √1 octahedron surrounds the √1 tetrahedron which surrounds the √0.𝚫 tetrahedron, as three concentric hulls. This 14-vertex 4-polytope is a 4-pyramid with a regular octahedron base: not a canonical octahedral pyramid with one apex (which has only 7 vertices) but an irregular truncated octahedral pyramid. Because its base is a regular octahedron which is a 24-cell octahedral cell, this 4-pyramid lies on the surface of the 24-cell.
- ↑ The apex of a canonical √1 octahedral pyramid has been truncated into a regular tetrahedral cell with shorter √0.𝚫 edges, replacing the apex with four vertices. The truncation has also created another four vertices (arranged as a √1 tetrahedron in a hyperplane between the octahedral base and the apex tetrahedral cell), and linked these eight new vertices with √0.𝚫 edges. The truncated pyramid thus has eight 'apex' vertices above the hyperplane of its octahedral base, rather than just one apex: 14 vertices in all. The original pyramid had flat sides: the five geodesic routes from any base vertex to the opposite base vertex ran along two √1 edges (and just one of those routes ran through the single apex). The truncated pyramid has rounded sides: five geodesic routes from any base vertex to the opposite base vertex run along three √0.𝚫 edges (and pass through two 'apexes').
- ↑ The uniform 4-polytopes which this 14-vertex, 25-cell irregular 4-polytope most closely resembles may be the 10-vertex, 10-cell rectified 5-cell and its dual (it has characteristics of both).
- ↑ 76.0 76.1 The annular ring gaps between icosahedra are filled by a ring of 10 face-bonded tetrahedra that all meet at the vertex where the two icosahedra meet. This 10-cell ring is shaped like a pentagonal antiprism which has been hollowed out like a bowl on both its top and bottom sides, so that it has zero thickness at its center. This center vertex, like all the other vertices of the 600-cell, is itself the apex of an icosahedral pyramid where 20 tetrahedra meet.[lower-alpha 62] Therefore the annular ring of 10 tetrahedra is itself an equatorial ring of an icosahedral pyramid, containing 10 of the 20 cells of its icosahedral pyramid.
- ↑ The 100-face surface of the triangular-faced 150-cell column could be scissors-cut lengthwise along a 10 edge path and peeled and laid flat as a 10×10 parallelogram of triangles.
- ↑ Because the 100-face surface of the 150-cell torus is alternately convex and concave, 100 tetrahedra stack on it in face-bonded pairs, as 50 triangular bipyramids which share one raised vertex and bury one formerly exposed valley edge. The triangular bipyramids are vertex-bonded to each other in 5 parallel lines of 5 bipyramids (10 tetrahedra) each, which run straight up and down the outside surface of the 150-cell column.
- ↑ 5 decagons spiral clockwise and 5 spiral counterclockwise, intersecting each other at the 50 valley vertices.
- ↑ The same 10-face belt of an icosahedral pyramid is an annular ring of 10 tetrahedra around the apex.[lower-alpha 76]
- ↑ 81.0 81.1 81.2 The 600-cell's Petrie polygon is a skew triacontagon {30}. It can be seen in orthogonal projection as the circumference of a triacontagram {30/3}=3{10} helix which zig-zags 60° left and right, bridging the space between the 3 Clifford parallel great decagons of the 30-cell ring. In the completely orthogonal plane it projects to the regular triacontagram {30/11}.[58]
- ↑ 82.0 82.1 The 30 vertices of the Boerdijk–Coxeter triple-helix ring lie in 3 decagonal central planes which intersect only at one point (the center of the 600-cell), even though they are not completely orthogonal or orthogonal at all: they are π/5 apart.[lower-alpha 47] Their decagonal great circles are Clifford parallel: one 600-cell edge-length apart at every point.[lower-alpha 33] They are ordinary 2-dimensional great circles, not helices, but they are linked Clifford parallel circles.
- ↑ 83.0 83.1 83.2 Isoclinic geodesics are 4-dimensional great circles in the sense that they are 1-dimensional geodesic lines that curve in 4-space in two completely orthogonal planes at once. They should not be confused with great 2-spheres,[69] which are the 4-space analogues[lower-alpha 2] of 2-dimensional great circles in 3-space (great 1-spheres).
- ↑ The 20 30-cell rings are chiral objects; they either spiral clockwise (right) or counterclockwise (left). The 150-cell torus (formed by five cell-disjoint 30-cell rings of the same chirality surrounding a great decagon) is not itself a chiral object, since it can be decomposed into either five parallel left-handed rings or five parallel right-handed rings. Unlike the 20-cell rings, the 150-cell tori are directly congruent with no torsion, like the octahedral 6-cell rings of the 24-cell. Each great decagon has five left-handed 30-cell rings surrounding it, and also five right-handed 30-cell rings surrounding it; but left-handed and right-handed 30-cell rings are not cell-disjoint and belong to different distinct rotations: the left and right rotations of the same fibration. In either distinct isoclinic rotation (left or right), the vertices of the 600-cell move along the axial 15-gram isoclines of 20 left 30-cell rings or 20 right 30-cell rings. Thus the great decagons, the 30-cell rings, and the 150-cell tori all occur as sets of Clifford parallel interlinked circles,[lower-alpha 33] although the exact way they nest together, avoid intersecting each other, and pass through each other to form a Hopf link is not identical for these three different kinds of Clifford parallel polytopes, in part because the linked pairs are variously of no inherent chirality (the decagons), the same chirality (the 30-cell rings), or no net torsion and both left and right interior organization (the 150-cell tori) but tracing the same chirality of interior organization in any distinct left or right rotation.
- ↑ A point on the icosahedron Hopf map[lower-alpha 49] of the 600-cell's decagonal fibration lifts to a great decagon; a triangular face lifts to a 30-cell ring; and a pentagonal pyramid of 5 faces lifts to a 150-cell torus.[54] In the grand antiprism decomposition, two completely disjoint 150-cell tori are lifted from antipodal pentagons, leaving an equatorial ring of 10 icosahedron faces between them: a Petrie decagon of 10 triangles, which lift to 10 30-cell rings. The two completely disjoint 150-cell tori contain 12 disjoint (Clifford parallel) decagons and all 120 vertices, so they comprise a complete Hopf fibration; there is no room for more 150-cell tori of this kind. To get a decomposition of the 600-cell into four 150-cell tori of this kind, the icosahedral map would have to be decomposed into four pentagons, centered at the vertices of an inscribed tetrahedron, and the icosahedron cannot be decomposed that way.
- ↑ Sadoc describes the decomposition of the 600-cell into four tori.[37] It is the same fibration of 12 great decagons and 20 30-cell rings, seen as a fibration of four completely disjoint 30-cell rings[lower-alpha 10] with spaces between them, which still encompasses all 12 decagons and all 120 vertices. If we look closely at the spaces between the four disjoint 30-cell rings, we can discern four 150-cell rings of 5 30-cell rings each. But these 150-cell rings do not have 5 30-cell rings around a common decagon axis, and 6 decagons each. Their axis is a 30-cell ring, not a decagon, and they contain only 3 decagons each. To construct them, on each of the four completely disjoint 30-cell rings, face-bond three more 30-cell rings to the exterior faces, making four stellated ("bumpy") rings containing four 30-cell rings (120 cells) each. Collectively they contain 16 of the 20 30-cell rings: there are still four 30-cell ring "holes" left to fill in the 600-cell. To do that, fill some of the surface concavities of each 120-tetrahedron ring by wrapping a fifth 30-cell ring around its circumference, completely orthogonal to the axial 30-cell ring you started with. The result is four 150-cell tori, of 5 30-cell rings each, each having two completely orthogonal 30-cell ring axes, either of which can be seen as either an axis or a circumference: it is both. On the icosahedron Hopf map,[lower-alpha 49] the four 30-cell rings lift from a star of four icosahedron faces (three faces edge-bonded around one). The fifth 30-cell ring lifts from a fifth face edge-bonded to the star, a sort of "extra flap" like the sixth square flap of the net of a cube before you fold it up into a cube. It does not matter which of the six possible adjacent faces you choose as the flap, but the choice determines the choice for all four 150-cell rings. There are six choices because there are six decagonal fibrations; this is when you fix which fibration you are taking. Thus every 30-cell ring is the center core of a 150-cell ring.
- ↑ 87.0 87.1 (Coxeter 1973) uses the greek letter 𝝓 (phi) to represent one of the three characteristic angles 𝟀, 𝝓, 𝟁 of a regular polytope. Because 𝝓 is commonly used to represent the golden ratio constant ≈ 1.618, for which Coxeter uses 𝝉 (tau), we reverse Coxeter's conventions, and use 𝝉 to represent the characteristic angle.
- ↑ An orthoscheme is a chiral irregular simplex with right triangle faces that is characteristic of some polytope if it will exactly fill that polytope with the reflections of itself in its own facets (its mirror walls). Every regular polytope can be dissected radially into instances of its characteristic orthoscheme surrounding its center. The characteristic orthoscheme has the shape described by the same Coxeter-Dynkin diagram as the regular polytope without the generating point ring.
- ↑ The four edges of each 4-orthoscheme which meet at the center of a regular 4-polytope are of unequal length, because they are the four characteristic radii of the regular 4-polytope: a vertex radius, an edge center radius, a face center radius, and a cell center radius. The five vertices of the 4-orthoscheme always include one regular 4-polytope vertex, one regular 4-polytope edge center, one regular 4-polytope face center, one regular 4-polytope cell center, and the regular 4-polytope center. Those five vertices (in that order) comprise a path along four mutually perpendicular edges (that makes three right angle turns), the characteristic feature of a 4-orthoscheme. The 4-orthoscheme has five dissimilar 3-orthoscheme facets.
- ↑ The reflecting surface of a (3-dimensional) polyhedron consists of 2-dimensional faces; the reflecting surface of a (4-dimensional) polychoron consists of 3-dimensional cells.
- ↑ 91.0 91.1 91.2 91.3 91.4 91.5 91.6 An isoclinic rotation by 36° is two simple rotations by 36° at the same time.[lower-alpha 129] It moves all the vertices 60° at the same time, in various different directions. Fifteen successive diagonal rotational increments, of 36°×36° each, move each vertex 900° through 15 vertices on a Möbius double loop of circumference 5𝝅 called an isocline, winding around the 600-cell and back to its point of origin, in one-and-one-half the time (15 rotational increments) that it would take a simple rotation to take the vertex once around the 600-cell on an ordinary {10} great circle (in 10 rotational increments).[lower-alpha 97] The helical double loop 5𝝅 isocline is just a special kind of single full circle, of 1.5 the period (15 chords instead of 10) as the simple great circle. The isocline is one true circle, as perfectly round and geodesic as the simple great circle, even through its chords are φ longer, its circumference is 5𝝅 instead of 2𝝅, it circles through four dimensions instead of two, and it acts in two chiral forms (left and right) even though all such circles of the same circumference are directly congruent. Nevertheless, to avoid confusion we always refer to it as an isocline and reserve the term great circle for an ordinary great circle in the plane.[lower-alpha 42]
- ↑ 92.0 92.1 92.2 92.3 92.4 92.5 Any double rotation (including an isoclinic rotation) can be seen as the composition of two simple rotations a and b: the left double rotation as a then b, and the right double rotation as b then a. Simple rotations are not commutative; left and right rotations (in general) reach different destinations. The difference between a double rotation and its two composing simple rotations is that the double rotation is 4-dimensionally diagonal: each moving vertex reaches its destination directly without passing through the intermediate point touched by a then b, or the other intermediate point touched by b then a, by rotating on a single helical geodesic (so it is the shortest path).[lower-alpha 58] Conversely, any simple rotation can be seen as the composition of two equal-angled double rotations (a left isoclinic rotation and a right isoclinic rotation), as discovered by Cayley; perhaps surprisingly, this composition is commutative, and is possible for any double rotation as well.[68]
- ↑ Cayley showed that any rotation in 4-space can be decomposed into two isoclinic rotations,[lower-alpha 92] which intuitively we might see follows from the fact that any transformation from one inertial reference frame to another is expressable as a rotation in 4-dimensional Euclidean space.
- ↑ 94.0 94.1 The 600-cell has 7200 distinct rotational displacements, each with its invariant rotation plane. The 7200 distinct central planes can be grouped into sets of Clifford parallel invariant rotation planes of 25 distinct isoclinic rotations, and are usually given as those sets.[71]
- ↑ 95.0 95.1 Isoclinic rotations take each vertex to a non-adjacent vertex at least two edge-lengths away. In the characteristic isoclinic rotations of the 5-cell, 16-cell, 24-cell and 600-cell, the non-adjacent vertex is exactly two edge-lengths away along one of several great circle geodesic routes: the opposite vertex of a neighboring cell. In the 8-cell it is three zig-zag edge-lengths away in the same cell: the opposite vertex of a cube. In the 120-cell it is four zig-zag edges away in the same cell: the opposite vertex of a dodecahedron.
- ↑ 96.0 96.1 96.2 In an isoclinic rotation, each point anywhere in the 4-polytope moves an equal distance in four orthogonal directions at once, on a 4-dimensional diagonal.[lower-alpha 42] The point is displaced a total Pythagorean distance equal to the square root of four times the square of that distance. All vertices are displaced to a vertex at least two edge-lengths away.[lower-alpha 95] For example, when the unit-radius 600-cell rotates isoclinically 36 degrees in a decagon invariant plane and 36 degrees in its completely orthogonal invariant plane,[lower-alpha 41] each vertex is displaced to another vertex √1 (60°) distant, moving √1/4 = 1/2 unit radius in four orthogonal directions.
- ↑ 97.0 97.1 97.2 Because the 600-cell's helical pentadecagram2 geodesic is bent into a twisted ring in the fourth dimension like a Möbius strip, its screw thread doubles back across itself after each revolution, without ever reversing its direction of rotation (left or right). The 30-vertex isoclinic path follows a Möbius double loop, forming a single continuous 15-vertex loop traversed in two revolutions. The Möbius helix is a geodesic "straight line" or isocline. The isocline connects the vertices of a lower frequency (longer wavelength) skew polygram than the Petrie polygon. The Petrie triacontagon has √0.𝚫 edges; the isoclinic pentadecagram2 has √1 edges which join vertices which are two √0.𝚫 edges apart. Each √1 edge belongs to a different great hexagon, and successive √1 edges belong to different 24-cells, as the isoclinic rotation takes hexagons to Clifford parallel hexagons and passes through successive Clifford parallel 24-cells.
- ↑ 98.0 98.1 All isoclines are geodesics, and isoclines on the 3-sphere are circles (curving equally in each dimension), but not all isoclines on 3-manifolds in 4-space are circles.
- ↑ 99.0 99.1 99.2 99.3 Isoclinic rotations[lower-alpha 42] partition the 600 cells (and the 120 vertices) of the 600-cell into two disjoint subsets of 300 cells (and 60 vertices), even and odd (or black and white), which shift places among themselves on black or white isoclines, in a manner dimensionally analogous[lower-alpha 2] to the way the bishops' diagonal moves restrict them to the white or the black squares of the chessboard.[lower-alpha 127] The black and white subsets are also divided among black and white invariant great circle polygons of the isoclinic rotation. In a discrete rotation (as of a 4-polytope with a finite number of vertices) the black and white subsets correspond to sets of inscribed great polygons {p} in invariant great circle polygons {2p}. For example, in the 600-cell a black and a white great pentagon {5} are inscribed in an invariant great decagon {10} of the characteristic decagonal isoclinic rotation. Importantly, a black and white pair of polygons {p} of the same distinct isoclinic rotation are never inscribed in the same {2p} polygon; there is always a black and a white {p} polygon inscribed in each invariant {2p} polygon, but they belong to distinct isoclinic rotations: the left and right rotation of the same fibraton, which share the same set of invariant planes. Black (white) isoclines intersect only black (white) great {p} polygons, so each vertex is either black or white.
- ↑ 100.0 100.1 100.2 100.3 100.4 The chord-path of an isocline may be called the 4-polytope's Clifford polygon, as it is the skew polygonal shape of the rotational circles traversed by the 4-polytope's vertices in its characteristic Clifford displacement.[83] The isocline is a helical Möbius double loop which reverses its chirality twice in the course of a full double circuit. The two loops are both entirely contained within the same cell ring, where they both follow chords connecting even (odd) vertices: typically opposite vertices of adjacent cells, two edge lengths apart.[lower-alpha 99] Both "halves" of the double loop pass through each cell in the cell ring, but intersect only two even (odd) vertices in each even (odd) cell. Each pair of intersected vertices in an even (odd) cell lie opposite each other on the Möbius strip, exactly one edge length apart. Thus each cell has two helices passing through it, which are Clifford parallels[lower-alpha 33] of opposite chirality at each pair of parallel points. Globally these two helices are a single connected circle of both chiralities,[lower-alpha 91] with no net torsion. An isocline acts as a left (or right) isocline when traversed by a left (or right) rotation (of different fibrations).
- ↑ 101.0 101.1 Isoclines on the 3-sphere occur in non-intersecting pairs of even/odd coordinate parity.[lower-alpha 99] A single black or white isocline forms a Möbius loop called the {1,1} torus knot or Villarceau circle[70] in which each of two "circles" linked in a Möbius "figure eight" loop traverses through all four dimensions.[lower-alpha 100] The double loop is a true circle in four dimensions.[lower-alpha 91] Even and odd isoclines are also linked, not in a Möbius loop but as a Hopf link of two non-intersecting circles,[lower-alpha 33] as are all the Clifford parallel isoclines of a Hopf fiber bundle.
- ↑ 102.0 102.1 A rotation in 4-space is completely characterized by choosing an invariant plane and an angle and direction (left or right) through which it rotates, and another angle and direction through which its one completely orthogonal[lower-alpha 16] invariant plane rotates. Two rotational displacements are identical if they have the same pair of invariant planes of rotation, through the same angles in the same directions (and hence also the same chiral pairing of directions). Thus the general rotation in 4-space is a double rotation, characterized by two angles. A simple rotation is a special case in which one rotational angle is 0.[lower-alpha 92] An isoclinic rotation is a different special case, similar but not identical to two simple rotations through the same angle.[lower-alpha 42]
- ↑ 103.0 103.1 103.2 There is a single invariant plane in each simple rotation, and a completely orthogonal fixed plane. There are an infinite number of pairs of completely orthogonal[lower-alpha 16] invariant planes in each isoclinic rotation, all rotating through the same angle;[lower-alpha 59] nonetheless, not all central planes are invariant planes of rotation. The invariant planes of an isoclinic rotation constitute a fibration of the entire 4-polytope.[73] In every isoclinic rotation of the 600-cell taking vertices to vertices either 12 Clifford parallel great decagons, or 20 Clifford parallel great hexagons or 30 Clifford parallel great squares are invariant planes of rotation.
- ↑ In a Clifford displacement, also known as an isoclinic rotation, all the Clifford parallel[lower-alpha 33] invariant planes[lower-alpha 103] are displaced in four orthogonal directions (two completely orthogonal planes) at once: they are rotated by the same angle, and at the same time they are tilted sideways by that same angle. A Clifford displacement is 4-dimensionally diagonal.[lower-alpha 96] Every plane that is Clifford parallel to one of the completely orthogonal planes is invariant under the isoclinic rotation: all the points in the plane rotate in circles but remain in the plane, even as the whole plane rotates sideways. All central polygons (of every kind) rotate by the same angle (though not all do so invariantly), and are also displaced sideways by the same angle to a Clifford parallel polygon (of the same kind).
- ↑ The three 16-cells in the 24-cell are rotated by 60° (𝜋/3) isoclinically with respect to each other. Because an isoclinic rotation is a rotation in two completely orthogonal planes at the same time, this means their corresponding vertices are 120° (2𝜋/3) apart. In a unit-radius 4-polytope, vertices 120° apart are joined by a √3 chord.
- ↑ 106.0 106.1 106.2 Any isoclinic rotation by 𝜋/5 in decagonal invariant planes[lower-alpha 112] takes every central polygon, geodesic cell ring or inscribed 4-polytope[lower-alpha 9] in the 600-cell to a Clifford parallel polytope 𝜋/5 away.
- ↑ 107.0 107.1 Five 24-cells meet at each vertex of the 600-cell,[lower-alpha 12] so there are four different directions in which the vertices can move to rotate the 24-cell (or all the 24-cells at once in an isoclinic rotation[lower-alpha 106]) directly toward an adjacent 24-cell.
- ↑ 108.0 108.1 A disjoint 24-cell reached by an isoclinic rotation is not any of the four adjacent 24-cells; the double rotation[lower-alpha 102] takes it past (not through) the adjacent 24-cell it rotates toward,[lower-alpha 107] and left or right to a more distant 24-cell from which it is completely disjoint.[lower-alpha 10] The four directions reach 8 different 24-cells[lower-alpha 7] because in an isoclinic rotation each vertex moves in a spiral along two completely orthogonal great circles at once. Four paths are right-hand threaded (like most screws and bolts), moving along the circles in the "same" directions, and four are left-hand threaded (like a reverse-threaded bolt), moving along the circles in what we conventionally say are "opposite" directions (according to the right hand rule by which we conventionally say which way is "up" on each of the 4 coordinate axes).[74]
- ↑ All isoclinic polygons are Clifford parallels (completely disjoint).[lower-alpha 10] Polyhedra (3-polytopes) and polychora (4-polytopes) may be isoclinic and not disjoint, if all of their corresponding central polygons are either Clifford parallel, or cocellular (in the same hyperplane) or coincident (the same object, shared). For example, the 24-cell, 600-cell and 120-cell contain pairs of inscribed tesseracts (8-cells) which are isoclinically rotated by 𝜋/3 with respect to each other, yet are not disjoint: they share a 16-cell (8 vertices, 6 great squares and 4 octahedral central hyperplanes), and some corresponding pairs of their great squares are cocellular (intersecting) rather than Clifford parallel (disjoint).
- ↑ 110.0 110.1 110.2 At each vertex, a 600-cell has four adjacent (non-disjoint)[lower-alpha 10] 24-cells that can each be reached by a simple rotation in that direction.[lower-alpha 107] Each 24-cell has 4 great hexagons crossing at each of its vertices, one of which it shares with each of the adjacent 24-cells; in a simple rotation that hexagonal plane remains fixed (its vertices do not move) as the 600-cell rotates around the common hexagonal plane. The 24-cell has 16 great hexagons altogether, so it is adjacent (non-disjoint) to 16 other 24-cells.[lower-alpha 7] In addition to being reachable by a simple rotation, each of the 16 can also be reached by an isoclinic rotation in which the shared hexagonal plane is not fixed: it rotates (non-invariantly) through 𝜋/5. The double rotation reaches an adjacent 24-cell directly as if indirectly by two successive simple rotations:[lower-alpha 92] first to one of the other adjacent 24-cells, and then to the destination 24-cell (adjacent to both of them).
- ↑ 111.0 111.1 In the 600-cell, there is a simple rotation which will take any vertex directly to any other vertex, also moving most or all of the other vertices but leaving at most 6 other vertices fixed (the vertices that the fixed central plane intersects). The vertex moves along a great circle in the invariant plane of rotation between adjacent vertices of a great decagon, a great hexagon, a great square or a great digon,[lower-alpha 48] and the completely orthogonal fixed plane intersects 0 vertices (a 30-gon),[lower-alpha 41] 2 vertices (a digon), 4 vertices (a square) or 6 vertices (a hexagon) respectively. Two non-disjoint 24-cells are related by a simple rotation through 𝜋/5 of the digon central plane completely orthogonal to their common hexagonal central plane. In this simple rotation, the hexagon does not move. The two non-disjoint 24-cells are also related by an isoclinic rotation in which the shared hexagonal plane does move.[lower-alpha 110]
- ↑ Any isoclinic rotation in a decagonal invariant plane is an isoclinic rotation in 24 invariant planes: 12 Clifford parallel decagonal planes,[lower-alpha 103] and the 12 Clifford parallel 30-gon planes completely orthogonal to each of those decagonal planes.[lower-alpha 41] As the invariant planes rotate in two completely orthogonal directions at once,[lower-alpha 58] all points in the planes move with them (stay in their planes and rotate with them), describing helical isoclines[lower-alpha 42] through 4-space. Note however that in a discrete decagonal fibration of the 600-cell (where 120 vertices are the only points considered), the 12 30-gon planes contain no points.
- ↑ 113.0 113.1 Notice the apparent incongruity of rotating hexagons by 𝜋/5, since only their opposite vertices are an integral multiple of 𝜋/5 apart. However, recall that 600-cell vertices which are one hexagon edge apart are exactly two decagon edges and two tetrahedral cells (one triangular dipyramid) apart. The hexagons have their own 10 discrete fibrations and cell rings, not Clifford parallel to the decagonal fibrations but also by fives[lower-alpha 14] in that five 24-cells meet at each vertex, each pair sharing a hexagon.[lower-alpha 12] Each hexagon rotates non-invariantly by 𝜋/5 in a hexagonal isoclinic rotation between non-disjoint 24-cells.[lower-alpha 110] Conversely, in all 𝜋/5 isoclinic rotations in decagonal invariant planes, all the vertices travel along isoclines[lower-alpha 42] which follow the edges of hexagons.
- ↑ 114.0 114.1 114.2 All 3-sphere isoclines[lower-alpha 42] of the same circumference are directly congruent circles.[lower-alpha 98] An ordinary great circle is an isocline of circumference 2𝝅; simple rotations take place on 2𝝅 isoclines. Double rotations may have isoclines of up to 8𝝅 circumference. Because the characteristic rotations of several regular 4-polytopes take place in the same invariant planes (the 24-cell's hexagonal planes), those rotations all have congruent isoclines of 4𝝅 circumference. The regular 4-polytopes which rotate on 4𝝅 isoclines characteristically (when they are rotating in the isoclinic invariant planes containing their edges) are the 5-cell, the 8-cell, the 24-cell and the 120-cell.
- ↑ Consider the statement: In one full revolution of an isoclinic rotation, every point in the space loops exactly once through its great circle Hopf fiber. It can be found in the literature, expressed in the mathematical language of the Hopf fibration,[75] but as a plain language statement of Euclidean geometry, how exactly should we visualize it? It paints a clear picture of all the great circles of a Hopf fibration rotating as rigid wheels, in parallel. That is a correct visualization, except for the fact that points moving under isoclinic rotation traverse an invariant great circle only in the sense that they stay on that circle as the whole circle itself is tilting sideways, rotating in parallel with the completely orthogonal great circle.[lower-alpha 42] With respect to the stationary reference frame, the points move diagonally on a helical isocline, they do not move on a planar great circle.[lower-alpha 58] Each helical isocline is itself a kind of circle, but it is not a planar great circle of the Hopf fibration: it is a special kind of geodesic circle whose circumference is greater than 2𝝅r, and it is not pictured explicitly at all by the plain statement we are trying to visualize. We cannot easily visualize this statement about the Hopf great circles in a stationary reference frame. The statement does not simply mean that in an isoclinic rotation every point on a stationary Hopf great circle loops through its stationary great circle. Rather, it means that every point on every Hopf great circle loops through its great circle as every great circle itself is moving orthogonally, flipping like a coin in the plane completely orthogonal to its own plane (at any instant, because of course the completely orthogonal plane is moving too). This simultaneous twisting rotation in two completely orthogonal planes is a double rotation; if the angle of rotation in the two completely orthogonal planes is exactly the same, it is isoclinic. An isoclinic rotation takes each rigid planar Hopf great circle to the stationary position of another Hopf great circle, while simultaneously each Hopf great circle also rotates like a wheel. This fibration of doubly rotating rigid wheels is undoubtably hard to visualize. In any graphical animation (whether actually rendered or merely imagined) it will be difficult to track the motions of the different rotating wheels, because Clifford parallel circles are not parallel in the ordinary sense, and every great circle is moving in a different direction at any one instant. There is one more way in which this simple statement belies the full complexity of the isoclinic motion. While it is true that every point loops through its Hopf great circle exactly once in a full isoclinic revolution, every vertex moves more than 360 degrees, as measured in the stationary reference frame. In any distinct isoclinic rotation, all the vertices move the same angular distance in the stationary reference frame in one full revolution, but each distinct pair of left-right isoclinic rotations corresponds to a unique Hopf fibration,[73] and the characteristic distance moved is different for each kind of Hopf fibration. For example, in the isoclinic rotation of a great hexagon fibration of the 24-cell, each vertex moves 720 degrees in the stationary reference frame (2 times the distance it moves within its moving Hopf great circle);[lower-alpha 114] but in the isoclinic rotation of a great decagon fibration of the 600-cell, each vertex moves 900 degrees in the stationary reference frame (2.5 times its great circle distance).
- ↑ 116.0 116.1 116.2 116.3 Each isocline has no inherent chirality but can act as either a left or right isocline; it is shared by a distinct left rotation and a distinct right rotation of different fibrations.
- ↑ 117.0 117.1 The analogous relationships among three kinds of {2p} isoclinic rotations, in Clifford parallel bundles of {4}, {6} or {10} great polygon invariant planes respectively, are at the heart of the complex nested relationship among the regular convex 4-polytopes.[lower-alpha 3] In the √1 hexagon {6} rotations characteristic of the 24-cell, the isocline chords (polygram edges) are simply √3 chords of the great hexagon, so the simple {6} hexagon rotation and the isoclinic {6/2} hexagram rotation both rotate circles of 6 vertices. The hexagram isocline, a special kind of great circle, has a circumference of 4𝝅 compared to the hexagon 2𝝅 great circle.[lower-alpha 122] The invariant central plane completely orthogonal to each {6} great hexagon is a {2} great digon,[lower-alpha 48] so an isoclinic {6} rotation of hexagrams is also a {2} rotation of axes.[lower-alpha 111] In the √2 square {4} rotations characteristic of the 16-cell, the isocline chords are √4 digon edges (axes), and the isocline polygram is an octagram, so the isocline has a circumference of 8𝝅. The isoclinic {8/2} octagram rotation rotates a circle of twice as many vertices as the simple {4} square rotation in the same time (number of rotational increments). The invariant central plane completely orthogonal to each {4} great square is another {4} great square just one isocline chord distant, so a right {4} rotation of squares is also a left {4} rotation of squares. The 16-cell's dual polytope the 8-cell tesseract inherits the same simple {4} and isoclinic {8/2} rotations, but its characteristic isoclinic rotation takes place in completely orthogonal invariant planes which contain a {4} great rectangle or a {2} great digon (from its successor the 24-cell). In the 8-cell this is a rotation of √1 × √3 great rectangles, and also a rotation of √4 axes, but it is the same isoclinic rotation as the 24-cell's characteristic rotation of great hexagons (in which the great rectangles are inscribed), as a consequence of the unique circumstance that the 8-cell and 24-cell have the same edge length. In the √0.𝚫 decagon {10} rotations characteristic of the 600-cell, the isocline chords are √1 hexagon edges, the isocline polygram is a pentadecagram, and the isocline has a circumference of 5𝝅.[lower-alpha 91] The isoclinic {15/2} pentadecagram rotation rotates a circle of {15} vertices in the same time as the simple decagon rotation of {10} vertices. The invariant central plane completely orthogonal to each (10) great decagon is a {0} great 0-gon,[lower-alpha 39] so a {10} rotation of decagons is also a {0} rotation of planes containing no vertices. The 600-cell's dual polytope the 120-cell inherits the same simple {10} and isoclinic {15/2} rotations, but its characteristic isoclinic rotation takes place in completely orthogonal invariant planes which contain {2} great digons (from its successor the 5-cell).[lower-alpha 123] This is a rotation of irregular great hexagons {6} of two alternating edge lengths (analogous to the tesseract's great rectangles), where the two different-length edges are three 120-cell edges and three 5-cell edges.
- ↑ Each discrete fibration of a regular convex 4-polytope is characterized by a unique left-right pair of isoclinic rotations and a unique bundle of great circle {2p} polygons (0 ≤ p ≤ 5) in the invariant planes of that pair of rotations. Each distinct rotation has a unique bundle of left (or right) {p} polygons inscribed in the {2p} polygons, and a unique bundle of skew {2p} polygrams which are its discrete left (or right) isoclines. The {p} polygons weave the {2p} polygrams into a bundle, and vice versa.
- ↑ The 600-cell has four orthogonal central hyperplanes, each of which is an icosidodecahedron.[lower-alpha 23]
- ↑ There are six congruent decagonal fibrations of the 600-cell. Choosing one decagonal fibration means choosing a bundle of 12 directly congruent Clifford parallel decagonal great circles, and a cell-disjoint set of 20 directly congruent 30-cell rings which tesselate the 600-cell. The fibration and its great circles are not chiral, but it has distinct left and right expressions in a left-right pair of isoclinic rotations. In the right (left) rotation the vertices move along a right (left) Hopf fiber bundle of Clifford parallel isoclines and intersect a right (left) Hopf fiber bundle of Clifford parallel great pentagons. The 30-cell rings are the only chiral objects, other than the bundles of isoclines or pentagons.[79] A right (left) pentagon bundle contains 12 great pentagons, inscribed in the 12 Clifford parallel great decagons. A right (left) isocline bundle contains 20 Clifford parallel pentadecagrams, one in each 30-cell ring.
- ↑ The composition of two simple 60° rotations in a pair of completely orthogonal invariant planes is a 60° isoclinic rotation in four pairs of completely orthogonal invariant planes.[lower-alpha 92] Thus the isoclinic rotation is the compound of four simple rotations, and all 24 vertices rotate in invariant hexagon planes, versus just 6 vertices in a simple rotation.
- ↑ 122.0 122.1 122.2 An isoclinic rotation by 60° is two simple rotations by 60° at the same time.[lower-alpha 121] It moves all the vertices 120° at the same time, in various different directions. Six successive diagonal rotational increments, of 60°x60° each, move each vertex through 720° on a Möbius double loop called an isocline, twice around the 24-cell and back to its point of origin, in the same time (six rotational units) that it would take a simple rotation to take the vertex once around the 24-cell on an ordinary great circle. The helical double loop 4𝝅 isocline is just another kind of single full circle, of the same time interval and period (6 chords) as the simple great circle. The isocline is one true circle,[lower-alpha 83] as perfectly round and geodesic as the simple great circle, even through its chords are √3 longer, its circumference is 4𝝅 instead of 2𝝅,[lower-alpha 114] it circles through four dimensions instead of two,[lower-alpha 101] and it acts in two chiral forms (left and right) even though all such circles of the same circumference are directly congruent.[lower-alpha 100] Nevertheless, to avoid confusion we always refer to it as an isocline and reserve the term great circle for an ordinary great circle in the plane.
- ↑ 120 regular 5-cells are inscribed in the 120-cell. The 5-cell has digon central planes, no two of which are orthogonal. It has 10 digon central planes, where each vertex pair is an edge, not an axis. The 5-cell is self-dual, so by reciprocation the 120-cell can be inscribed in a regular 5-cell of larger radius. Therefore the finite sequence of 6 regular 4-polytopes[lower-alpha 3] nested like Russian dolls can also be seen as an infinite sequence.
- ↑ In the 30-cell ring, each isocline runs from a vertex to a non-adjacent vertex in the third shell of vertices surrounding it. Three other vertices between these two vertices can be seen in the 30-cell ring, two adjacent in the first surrounding shell, and one in the second surrounding shell.
- ↑ Since it is difficult to color points and lines white, we sometimes use black and red instead of black and white. In particular, isocline chords are sometimes shown as black or red dashed lines.
- ↑ Chirality and even/odd parity are distinct flavors. Things which have even/odd coordinate parity are black or white: the squares of the chessboard,[lower-alpha 125] cells, vertices and the isoclines which connect them by isoclinic rotation.[lower-alpha 42] Everything else is black and white: e.g. adjacent face-bonded cell pairs, or edges and chords which are black at one end and white at the other. Things which have chirality come in right or left enantiomorphous forms: isoclinic rotations and chiral objects which include characteristic orthoschemes, pairs of Clifford parallel great polygon planes,[82] fiber bundles of Clifford parallel circles (whether or not the circles themselves are chiral), and the chiral cell rings found in the 16-cell and 600-cell. Things which have neither an even/odd parity nor a chirality include all edges and faces (shared by black and white cells), great circle polygons and their fibrations, and non-chiral cell rings such as the 24-cell's cell rings of octahedra. Some things have both an even/odd parity and a chirality: isoclines are black or white because they connect vertices which are all of the same color, and they act as left or right chiral objects when they are vertex paths in a left or right rotation, although they have no inherent chirality themselves.[lower-alpha 116] Each left (or right) rotation traverses an equal number of black and white isoclines.[lower-alpha 100]
- ↑ 127.0 127.1 Left and right isoclinic rotations partition the 600 cells (and 120 vertices) into black and white in the same way.[14] The rotations of all fibrations of the same kind of great polygon use the same chessboard, which is a convention of the coordinate system based on even and odd coordinates.[81] Left and right are not colors: in either a left (or right) rotation half the moving vertices are black, running along black isoclines through black vertices, and the other half are white vertices rotating among themselves.[lower-alpha 126]
- ↑ Each axis of the 600-cell touches a left isocline of each fibration at one end and a right isocline of the fibration at the other end. Each 30-cell ring's axial isocline passes through only one of the two antipodal vertices of each of the 30 (of 60) 600-cell axes that the isocline's 30-vertex, 30-cell ring touches (at only one end).
- ↑ The composition of two simple 36° rotations in a pair of completely orthogonal invariant planes is a 36° isoclinic rotation in twelve pairs of completely orthogonal invariant planes.[lower-alpha 92] Thus the isoclinic rotation is the compound of twelve simple rotations, and all 120 vertices rotate in invariant decagon planes, versus just 10 vertices in a simple rotation.
- ↑ The 24-cell rotates hexagons on hexagrams, while the 600-cell rotates hexagons on decagrams, but these are discrete instances of the same kind of isoclinic rotation in hexagon invariant planes. In particular, their congruent isoclines are all exactly the same geodesic circle of circumference 4𝝅.[lower-alpha 114] They have different isocline polygrams only because the isocline curve intersects more vertices in the 600-cell than it does in the 24-cell. The 600-cell's helical {20/6}=2{10/3} icosagram is a compound of the 24-cell's helical {6/2} hexagram, which is inscribed within it just as the 24-cell is inscribed in the 600-cell.
- ↑ The 16-cell rotates squares on {8/3} octagrams, while the 600-cell rotates squares on {24/5} 24-grams, but these are discrete instances of the same kind of isoclinic rotation in square invariant planes. In particular, their congruent isoclines are all exactly the same geodesic circle of circumference 8𝝅. They have different isocline polygrams only because the isocline curve intersects more vertices in the 600-cell than it does in the 16-cell. The 600-cell's helical {24/5} 24-gram is a compound of the 16-cell's helical {8/3} octagram, which is inscribed within it just as the 16-cell is inscribed in the 600-cell.
Citations
- ↑ N.W. Johnson: Geometries and Transformations, (2018) ISBN:978-1-107-10340-5 Chapter 11: Finite Symmetry Groups, 11.5 Spherical Coxeter groups, p.249
- ↑ Matila Ghyka, The Geometry of Art and Life (1977), p.68
- ↑ Coxeter 1973, pp. 292-293, Table I(ii): The sixteen regular polytopes {p,q,r} in four dimensions; An invaluable table providing all 20 metrics of each 4-polytope in edge length units. They must be algebraically converted to compare polytopes of unit radius.
- ↑ Coxeter 1973, p. 153, §8.51; "In fact, the vertices of {3, 3, 5}, each taken 5 times, are the vertices of 25 {3, 4, 3}'s."
- ↑ 5.0 5.1 Coxeter 1973, p. 305, Table VII: Regular Compounds in Four Dimensions.
- ↑ Coxeter 1973, pp. 156-157, §8.7 Cartesian coordinates.
- ↑ 7.0 7.1 Coxeter 1973, pp. 151-153, §8.4 The snub {3,4,3}.
- ↑ Waegell & Aravind 2009, pp. 3-4, §3.2 The 75 bases of the 600-cell; In the 600-cell the configuration's "points" and "lines" are axes ("rays") and 16-cells ("bases"), respectively.
- ↑ 9.0 9.1 Denney et al. 2020, p. 438.
- ↑ Zamboj 2021, pp. 10-11, §Hopf coordinates.
- ↑ Coxeter 1973, p. 298, Table V: The Distribution of Vertices of Four-dimensional Polytopes in Parallel Solid Sections (§13.1); (iii) Sections of {3, 3, 5} (edge 2𝜏−1) beginning with a vertex.
- ↑ Oss 1899; van Oss does not mention the arc distances between vertices of the 600-cell.
- ↑ Buekenhout & Parker 1998.
- ↑ 14.0 14.1 14.2 14.3 Dechant 2021, pp. 18-20, §6. The Coxeter Plane.
- ↑ Coxeter 1973, p. 298, Table V: The Distribution of Vertices of Four-dimensional Polytopes in Parallel Solid Sections (§13.1); (iii) Sections of {3, 3, 5} (edge 2𝜏−1) beginning with a vertex; see column a.
- ↑ Steinbach 1997, p. 23, Figure 3; Steinbach derived a formula relating the diagonals and edge lengths of successive regular polygons, and illustrated it with a "fan of chords" diagram like the one here.
- ↑ Baez, John (7 March 2017). "Pi and the Golden Ratio". https://johncarlosbaez.wordpress.com/2017/03/07/pi-and-the-golden-ratio/.
- ↑ 18.0 18.1 Denney et al. 2020, p. 434.
- ↑ Denney et al. 2020, pp. 437-439, §4 The planes of the 600-cell.
- ↑ Kim & Rote 2016, pp. 8-10, Relations to Clifford Parallelism.
- ↑ 21.0 21.1 Sadoc 2001, p. 576, §2.4 Discretising the fibration for the {3, 3, 5} polytope: the ten-fold screw axis.
- ↑ Waegell & Aravind 2009, p. 5, §3.4. The 24-cell: points, lines, and Reye's configuration; Here Reye's "points" and "lines" are axes and hexagons, respectively. The dual hexagon planes are not orthogonal to each other, only their dual axis pairs. Dual hexagon pairs do not occur in individual 24-cells, only between 24-cells in the 600-cell.
- ↑ 23.0 23.1 23.2 Sadoc 2001, pp. 576-577, §2.4 Discretising the fibration for the {3, 3, 5} polytope: the six-fold screw axis.
- ↑ 24.0 24.1 Sadoc 2001, p. 577, §2.4 Discretising the fibration for the {3, 3, 5} polytope: the four-fold screw axis.
- ↑ Copher 2019, p. 6, §3.2 Theorem 3.4.
- ↑ Kim & Rote 2016, p. 7, §6 Angles between two Planes in 4-Space; "In four (and higher) dimensions, we need two angles to fix the relative position between two planes. (More generally, k angles are defined between k-dimensional subspaces.)"
- ↑ Lemmens & Seidel 1973.
- ↑ Mamone, Pileio & Levitt 2010, p. 1433, §4.1; A Cartesian 4-coordinate point (w,x,y,z) is a vector in 4D space from (0,0,0,0). Four-dimensional real space is a vector space: any two vectors can be added or multiplied by a scalar to give another vector. Quaternions extend the vectorial structure of 4D real space by allowing the multiplication of two 4D vectors [math]\displaystyle{ \left(w,x,y,z\right)_1 }[/math] and [math]\displaystyle{ \left(w,x,y,z\right)_2 }[/math] according to
[math]\displaystyle{ \begin{pmatrix} w_2\\ x_2\\ y_2\\ z_2 \end{pmatrix} \begin{pmatrix} w_1\\ x_1\\ y_1\\ z_1 \end{pmatrix} = \begin{pmatrix} {w_2 w_1 - x_2 x_1 - y_2 y_1 - z_2 z_1}\\ {w_2 x_1 + x_2 w_1 + y_2 z_1 - z_2 y_1}\\ {w_2 y_1 - x_2 z_1 + y_2 w_1 + z_2 x_1}\\ {w_2 z_1 + x_2 y_1 - y_2 x_1 + z_2 w_1} \end{pmatrix} }[/math] - ↑ 29.0 29.1 Sadoc 2001, pp. 575-578, §2 Geometry of the {3,3,5}-polytope in S3; Sadoc studied all the Hopf fibrations of the 600-cell into sets of {4}, {6} or {10} great circle fibers on different screw axes, gave their Hopf maps, and fully illustrated the characteristic decagonal cell rings.
- ↑ Tyrrell & Semple 1971, pp. 6-7, §4. Isoclinic planes in Euclidean space E4.
- ↑ 31.0 31.1 31.2 Sadoc 2001, pp. 577-578, §2.5 The 30/11 symmetry: an example of other kind of symmetries.
- ↑ Coxeter 1973, p. 211, §11.x Historical remarks; "The finite group [32, 2, 1] is isomorphic with the group of incidence-preserving permutations of the 27 lines on the general cubic surface. (For the earliest description of these lines, see Schlafli 2.)".
- ↑ Schläfli 1858; this paper of Schläfli's describing the double six configuration was one of the only fragments of his discovery of the regular polytopes in higher dimensions to be published during his lifetime.[32]
- ↑ Coxeter 1973, pp. 141-144, §7. Ordinary Polytopes in Higher Space; §7.x. Historical remarks; "Practically all the ideas in this chapter ... are due to Schläfli, who discovered them before 1853 — a time when Cayley, Grassman and Möbius were the only other people who had ever conceived the possibility of geometry in more than three dimensions."
- ↑ Coxeter 1970, studied cell rings in the general case of their geometry and group theory, identifying each cell ring as a polytope in its own right which fills a three-dimensional manifold (such as the 3-sphere) with its corresponding honeycomb.[lower-alpha 52] He found that cell rings follow Petrie polygons and some (but not all) cell rings and their honeycombs are twisted, occurring in left- and right-handed chiral forms. Specifically, he found that the regular 4-polytopes with tetrahedral cells (5-cell, 16-cell, 600-cell) have twisted cell rings, and the others (whose cells have opposing faces) do not.[lower-alpha 53] Separately, he categorized cell rings by whether they form their honeycombs in hyperbolic or Euclidean space, the latter being those found in the 4-polytopes which can tile 4-space by translation to form Euclidean honeycombs (16-cell, 8-cell, 24-cell).
- ↑ Banchoff 2013, studied the decomposition of regular 4-polytopes into honeycombs of tori tiling the Clifford torus, showed how the honeycombs correspond to Hopf fibrations, and made decompositions composed of meridian and equatorial cell rings with illustrations.
- ↑ 37.0 37.1 Sadoc 2001, p. 578, §2.6 The {3, 3, 5} polytope: a set of four helices.
- ↑ Dechant 2021, §1. Introduction.
- ↑ Zamboj 2021.
- ↑ Sadoc & Charvolin 2009, §1.2 The curved space approach; studies the helical orientation of molecules in crystal structures and their imperfect packings ("frustrations") in 3-dimensional space. "The frustration, which arises when the molecular orientation is transported along the two [circular] AB paths of figure 1 [helix], is imposed by the very topological nature of the Euclidean space R3. It would not occur if the molecules were embedded in the non-Euclidean space of the 3-sphere S3, or hypersphere. This space with a homogeneous positive curvature can indeed be described by equidistant and uniformly twisted fibers,[lower-alpha 33] along which the molecules can be aligned without any conflict between compactness and torsion.... The fibres of this Hopf fibration are great circles of S3, the whole family of which is also called the Clifford parallels. Two of these fibers are C∞ symmetry axes for the whole fibration; each fibre makes one turn around each axis and regularly rotates when moving from one axis to another.[lower-alpha 58] These fibers build a double twist configuration while staying parallel, i.e. without any frustration, in the whole volume of S3.[lower-alpha 59] They can therefore be used as models to study the condensation of long molecules in the presence of a double twist constraint."
- ↑ 41.0 41.1 Coxeter 1973, p. 303, Table VI (iii): 𝐈𝐈 = {3,3,5}.
- ↑ Coxeter 1973, p. 153, §8.5 Gosset's construction for {3,3,5}.
- ↑ Borovik 2006; "The environment which directed the evolution of our brain never provided our ancestors with four-dimensional experiences.... [Nevertheless] we humans are blessed with a remarkable piece of mathematical software for image processing hardwired into our brains. Coxeter made full use of it, and expected the reader to use it.... Visualization is one of the most powerful interiorization techniques. It anchors mathematical concepts and ideas into one of the most powerful parts of our brain, the visual processing module. Coxeter Theory [of polytopes generated by] finite reflection groups allow[s] an approach to their study based on a systematic reduction of complex geometric configurations to much simpler two- and three-dimensional special cases."
- ↑ Miyazaki 1990; Miyazaki showed that the surface envelope of the 600-cell can be realized architecturally in our ordinary 3-dimensional space as physical buildings (geodesic domes).
- ↑ Coxeter 1973, pp. 50-52, §3.7.
- ↑ Coxeter 1973, p. 293; 164°29'
- ↑ Coxeter 1973, p. 298, Table V: The Distribution of Vertices of Four-dimensional Polytopes in Parallel Solid Sections.
- ↑ Coxeter 1973, pp. 50-52, §3.7: Coordinates for the vertices of the regular and quasi-regular solids.
- ↑ Itoh & Nara 2021, §4. From the 24-cell onto an octahedron; "This article addresses the 24-cell and gives a continuous flattening motion for its 2-skeleton [the cuboctahedron], which is related to the Jitterbug by Buckminster Fuller."
- ↑ Verheyen, H. F. (1989). "The complete set of Jitterbug transformers and the analysis of their motion". Computers and Mathematics with Applications 17 (1–3): 203–250. doi:10.1016/0898-1221(89)90160-0.
- ↑ Coxeter 1973, p. 299, Table V: (iv) Simplified sections of {3,3,5} ... beginning with a cell.
- ↑ Sadoc 2001, pp. 576-577, §2.4 Discretising the fibration for the {3, 3, 5}; "Let us now proceed to a toroidal decomposition of the {3, 3, 5} polytope."
- ↑ Coxeter 1970, pp. 19-23, §9. The 120-cell and the 600-cell.
- ↑ 54.0 54.1 Sadoc 2001, pp. 576-577, §2.4 Discretising the fibration for the {3, 3, 5}, Fig. 2. A five fold symmetry column; in caption (sic) dodecagons should be decagons.
- ↑ 55.0 55.1 55.2 Dechant 2021, pp. 20-22, §7. The Grand Antiprism and H2 × H2.
- ↑ Banchoff 1988.
- ↑ Zamboj 2021, pp. 6-12, §2 Mathematical background.
- ↑ Coxeter 1973, pp. 292-293, Table I(ii); 600-cell h1 h2.
- ↑ Coxeter 1973, pp. 292-293, Table I(ii); "600-cell".
- ↑ Coxeter 1973, p. 139, §7.9 The characteristic simplex.
- ↑ Coxeter 1973, p. 290, Table I(ii); "dihedral angles".
- ↑ Coxeter 1973, pp. 227−233, §12.7 A necklace of tetrahedral beads.
- ↑ Coxeter 1973, pp. 33-38, §3.1 Congruent transformations.
- ↑ Dechant 2017, pp. 410-419, §6. The Coxeter Plane; see p. 416, Table 1. Summary of the factorisations of the Coxeter versors of the 4D root systems; "Coxeter (reflection) groups in the Clifford framework ... afford a uniquely simple prescription for reflections. Via the Cartan-Dieudonné theorem, performing two reflections successively generates a rotation, which in Clifford algebra is described by a spinor that is simply the geometric product of the two vectors generating the reflections."
- ↑ Coxeter 1973, pp. 217-218, §12.2 Congruent transformations.
- ↑ Koca, Al-Ajmi & Ozdes Koca 2011, pp. 986-988, 6. Dual of the snub 24-cell.
- ↑ Mamone, Pileio & Levitt 2010, pp. 1438-1439, §4.5 Regular Convex 4-Polytopes; the 600-cell has 14,400 symmetry operations (rotations and reflections) as enumerated in Table 2, symmetry group 𝛨4.[lower-alpha 94]
- ↑ Perez-Gracia & Thomas 2017.
- ↑ Stillwell 2001, p. 24.
- ↑ Dorst 2019, p. 44, §1. Villarceau Circles; "In mathematics, the path that the (1, 1) knot on the torus traces is also known as a Villarceau circle. Villarceau circles are usually introduced as two intersecting circles that are the cross-section of a torus by a well-chosen plane cutting it. Picking one such circle and rotating it around the torus axis, the resulting family of circles can be used to rule the torus. By nesting tori smartly, the collection of all such circles then form a Hopf fibration.... we prefer to consider the Villarceau circle as the (1, 1) torus knot rather than as a planar cut."
- ↑ Mamone, Pileio & Levitt 2010, §4.5 Regular Convex 4-Polytopes, Table 2.
- ↑ Waegell & Aravind 2009, pp. 2-5, §3. The 600-cell.
- ↑ 73.0 73.1 Kim & Rote 2016, pp. 13-14, §8.2 Equivalence of an Invariant Family and a Hopf Bundle.
- ↑ 74.0 74.1 Perez-Gracia & Thomas 2017, pp. 12−13, §5. A useful mapping.
- ↑ Kim & Rote 2016, pp. 12-16, 8 The Construction of Hopf Fibrations; see Theorem 13.
- ↑ Perez-Gracia & Thomas 2017, pp. 2−3, §2. Isoclinic rotations.
- ↑ Kim & Rote 2016, p. 12-16, §8 The Construction of Hopf Fibrations; see §8.3.
- ↑ Perez-Gracia & Thomas 2017, §1. Introduction; "This article [will] derive a spectral decomposition of isoclinic rotations and explicit formulas in matrix and Clifford algebra for the computation of Cayley's [isoclinic] factorization."[lower-alpha 92]
- ↑ 79.0 79.1 79.2 Kim & Rote 2016, p. 14, §8.3 Corollary 9. Every great circle belongs to a unique right [(and left)] Hopf bundle.
- ↑ Kim & Rote 2016, pp. 14-16, §8.3 Properties of the Hopf Fibration.
- ↑ Coxeter 1973, p. 156: "...the chess-board has an n-dimensional analogue."
- ↑ Kim & Rote 2016, p. 8, Left and Right Pairs of Isoclinic Planes.
- ↑ Tyrrell & Semple 1971, pp. 34-57, Linear Systems of Clifford Parallels.
- ↑ Coxeter 1973, p. 12, §1.8. Configurations.
- ↑ van Ittersum 2020, pp. 80-95, §4.3.
- ↑ Steinbach 1997, p. 24.
- ↑ Stillwell 2001, p. 18-21.
- ↑ Stillwell 2001, pp. 22-23, The Poincaré Homology Sphere.
- ↑ Mebius 2015, p. 1, "Quaternion algebra is the tool par excellence for the treatment of three- and four- dimensional (3D and 4D) rotations. Obviously only 3D and by implication 2D rotations have an everyday practical meaning, but the theory of 4D rotations turns out to offer the easiest road to the representation of 3D rotations by quaternions.".
- ↑ Denney et al. 2020, §2 The Labeling of H4.
- ↑ Oss 1899, pp. 1-18.
- ↑ Dechant 2021, Abstract; "[E]very 3D root system allows the construction of a corresponding 4D root system via an 'induction theorem'. In this paper, we look at the icosahedral case of H3 → H4 in detail and perform the calculations explicitly. Clifford algebra is used to perform group theoretic calculations based on the versor theorem and the Cartan-Dieudonné theorem ... shed[ding] light on geometric aspects of the H4 root system (the 600-cell) as well as other related polytopes and their symmetries ... including the construction of the Coxeter plane, which is used for visualising the complementary pairs of invariant polytopes.... This approach therefore constitutes a more systematic and general way of performing calculations concerning groups, in particular reflection groups and root systems, in a Clifford algebraic framework."
- ↑ Grossman, Wendy A.; Sebline, Edouard, eds. (2015), Man Ray Human Equations: A journey from mathematics to Shakespeare, Hatje Cantz. See in particular mathematical object mo-6.2, p. 58; Antony and Cleopatra, SE-6, p. 59; mathematical object mo-9, p. 64; Merchant of Venice, SE-9, p. 65, and "The Hexacosichoron", Philip Ordning, p. 96.
- ↑ Dechant 2021, pp. 22-24, §8. Snub 24-cell.
- ↑ Sikiric, Mathieu; Myrvold, Wendy (2007). "The special cuts of 600-cell". Beiträge zur Algebra und Geometrie 49 (1).
- ↑ Denney et al. 2020.
- ↑ Coxeter 1991, pp. 48-49.
References
- Schläfli, Ludwig (1858), Cayley, Arthur, ed., "An attempt to determine the twenty-seven lines upon a surface of the third order, and to derive such surfaces in species, in reference to the reality of the lines upon the surface", Quarterly Journal of Pure and Applied Mathematics 2: 55–65, 110–120, http://resolver.sub.uni-goettingen.de/purl?PPN600494829_0002
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
- Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge: Cambridge University Press.
- Coxeter, H.S.M. (1995). Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C. et al.. eds. Kaleidoscopes: Selected Writings of H.S.M. Coxeter (2nd ed.). Wiley-Interscience Publication. ISBN 978-0-471-01003-6. https://www.wiley.com/en-us/Kaleidoscopes%3A+Selected+Writings+of+H+S+M+Coxeter-p-9780471010036.
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Coxeter, H.S.M. (1970), "Twisted Honeycombs", Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics (Providence, Rhode Island: American Mathematical Society) 4
- Borovik, Alexandre (2006). "Coxeter Theory: The Cognitive Aspects". in Davis, Chandler; Ellers, Erich. The Coxeter Legacy. Providence, Rhode Island: American Mathematical Society. pp. 17–43. ISBN 978-0821837221. https://www.academia.edu/26091464.
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [1]
- Oss, Salomon Levi van (1899). "Das regelmässige Sechshundertzell und seine selbstdeckenden Bewegungen". Verhandelingen der Koninklijke (Nederlandse) Akademie van Wetenschappen, Sectie 1 (Afdeeling Natuurkunde) (Amsterdam) 7 (1): 1–18. https://books.google.com/books?id=AfQ3AQAAMAAJ&pg=PA3.
- Buekenhout, F.; Parker, M. (15 May 1998). "The number of nets of the regular convex polytopes in dimension <= 4". Discrete Mathematics 186 (1–3): 69–94. doi:10.1016/S0012-365X(97)00225-2.
- Denney, Tomme; Hooker, Da'Shay; Johnson, De'Janeke; Robinson, Tianna; Butler, Majid; Claiborne, Sandernishe (2020). "The geometry of H4 polytopes". Advances in Geometry 20 (3): 433–444. doi:10.1515/advgeom-2020-0005.
- Steinbach, Peter (1997). "Golden fields: A case for the Heptagon". Mathematics Magazine 70 (Feb 1997): 22–31. doi:10.1080/0025570X.1997.11996494.
- Copher, Jessica (2019). "Sums and Products of Regular Polytopes' Squared Chord Lengths". arXiv:1903.06971 [math.MG].
- Miyazaki, Koji (1990). "Primary Hypergeodesic Polytopes". International Journal of Space Structures 5 (3–4): 309–323. doi:10.1177/026635119000500312.
- van Ittersum, Clara (2020). Symmetry groups of regular polytopes in three and four dimensions (Thesis). Delft University of Technology.
- Waegell, Mordecai; Aravind, P. K. (2009-11-12). "Critical noncolorings of the 600-cell proving the Bell-Kochen-Specker theorem" (in en). Journal of Physics A 43 (10): 105304. doi:10.1088/1751-8113/43/10/105304.
- Zamboj, Michal (8 Jan 2021). "Synthetic construction of the Hopf fibration in a double orthogonal projection of 4-space". Journal of Computational Design and Engineering 8 (3): 836–854. doi:10.1093/jcde/qwab018.
- Kim, Heuna; Rote, G. (2016). "Congruence Testing of Point Sets in 4 Dimensions". arXiv:1603.07269 [cs.CG].
- Sadoc, Jean-Francois (2001). "Helices and helix packings derived from the {3,3,5} polytope". European Physical Journal E 5: 575–582. doi:10.1007/s101890170040. https://www.researchgate.net/publication/260046074.
- Sadoc, J F; Charvolin, J (2009). "3-sphere fibrations: A tool for analyzing twisted materials in condensed matter". Journal of Physics A 42 (46): 465209. doi:10.1088/1751-8113/42/46/465209. Bibcode: 2009JPhA...42T5209S. https://stacks.iop.org/JPhysA/42/465209.
- Lemmens, P.W.H.; Seidel, J.J. (1973). "Equi-isoclinic subspaces of Euclidean spaces". Indagationes Mathematicae (Proceedings) 76 (2): 98–107. doi:10.1016/1385-7258(73)90042-5. ISSN 1385-7258. https://dx.doi.org/10.1016/1385-7258%2873%2990042-5.
- Tyrrell, J. A.; Semple, J.G. (1971). Generalized Clifford parallelism. Cambridge University Press. ISBN 0-521-08042-8. https://archive.org/details/generalizedcliff0000tyrr.
- Perez-Gracia, Alba; Thomas, Federico (2017). "On Cayley's Factorization of 4D Rotations and Applications". Adv. Appl. Clifford Algebras 27: 523–538. doi:10.1007/s00006-016-0683-9. https://upcommons.upc.edu/bitstream/handle/2117/113067/1749-ON-CAYLEYS-FACTORIZATION-OF-4D-ROTATIONS-AND-APPLICATIONS.pdf.
- Mamone, Salvatore; Pileio, Giuseppe; Levitt, Malcolm H. (2010). "Orientational Sampling Schemes Based on Four Dimensional Polytopes". Symmetry 2 (3): 1423–1449. doi:10.3390/sym2031423. Bibcode: 2010Symm....2.1423M.
- Stillwell, John (January 2001). "The Story of the 120-Cell". Notices of the AMS 48 (1): 17–25. https://www.ams.org/notices/200101/fea-stillwell.pdf.
- Dorst, Leo (2019). "Conformal Villarceau Rotors". Advances in Applied Clifford Algebras 29 (44). doi:10.1007/s00006-019-0960-5.
- Banchoff, Thomas F. (2013). "Torus Decompostions of Regular Polytopes in 4-space". in Senechal, Marjorie. Shaping Space. Springer New York. pp. 257–266. doi:10.1007/978-0-387-92714-5_20. ISBN 978-0-387-92713-8. https://archive.org/details/shapingspaceexpl00sene.
- Banchoff, Thomas (1988). "Geometry of the Hopf Mapping and Pinkall's Tori of Given Conformal Type". in Tangora, Martin. Computers in Algebra. New York and Basel: Marcel Dekker. pp. 57–62.
- Koca, Mehmet; Ozdes Koca, Nazife; Al-Barwani, Muataz (2012). "Snub 24-Cell Derived from the Coxeter-Weyl Group W(D4)". Int. J. Geom. Methods Mod. Phys. 09 (8). doi:10.1142/S0219887812500685. http://arxiv-web3.library.cornell.edu/abs/1106.3433.
- Koca, Mehmet; Al-Ajmi, Mudhahir; Ozdes Koca, Nazife (2011). "Quaternionic representation of snub 24-cell and its dual polytope derived from E8 root system". Linear Algebra and Its Applications 434 (4): 977–989. doi:10.1016/j.laa.2010.10.005. ISSN 0024-3795.
- Dechant, Pierre-Philippe (2021). "Clifford Spinors and Root System Induction: H4 and the Grand Antiprism". Advances in Applied Clifford Algebras (Springer Science and Business Media) 31 (3). doi:10.1007/s00006-021-01139-2.
- Dechant, Pierre-Philippe (2017). "The E8 Geometry from a Clifford Perspective". Advances in Applied Clifford Algebras 27: 397–421. doi:10.1007/s00006-016-0675-9.
- Itoh, Jin-ichi; Nara, Chie (2021). "Continuous flattening of the 2-dimensional skeleton of a regular 24-cell". Journal of Geometry 112 (13). doi:10.1007/s00022-021-00575-6.
- Mebius, Johan (July 2015) [11 Jan 1994]. Applications of Quaternions to Dynamical Simulation, Computer Graphics and Biomechanics (Thesis). Delft University of Technology. doi:10.13140/RG.2.1.3310.3205.
External links
- Weisstein, Eric W.. "600-Cell". http://mathworld.wolfram.com/600-Cell.html.
- Klitzing, Richard. "4D uniform polytopes (polychora) x3o3o5o - ex". https://bendwavy.org/klitzing/dimensions/polychora.htm.
- Der 600-Zeller (600-cell) Marco Möller's Regular polytopes in R4 (German)
- The 600-Cell Vertex centered expansion of the 600-cell
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |