Representation theory of finite groups

Short description: Representations of finite groups, particularly on vector spaces

The representation theory of groups is a part of mathematics which examines how groups act on given structures.

Here the focus is in particular on operations of groups on vector spaces. Nevertheless, groups acting on other groups or on sets are also considered. For more details, please refer to the section on permutation representations.

Other than a few marked exceptions, only finite groups will be considered in this article. We will also restrict ourselves to vector spaces over fields of characteristic zero. Because the theory of algebraically closed fields of characteristic zero is complete, a theory valid for a special algebraically closed field of characteristic zero is also valid for every other algebraically closed field of characteristic zero. Thus, without loss of generality, we can study vector spaces over [math]\displaystyle{ \Complex. }[/math]

Representation theory is used in many parts of mathematics, as well as in quantum chemistry and physics. Among other things it is used in algebra to examine the structure of groups. There are also applications in harmonic analysis and number theory. For example, representation theory is used in the modern approach to gain new results about automorphic forms.

Definition

Linear representations

Let [math]\displaystyle{ V }[/math] be a [math]\displaystyle{ K }[/math]–vector space and [math]\displaystyle{ G }[/math] a finite group. A linear representation of [math]\displaystyle{ G }[/math] is a group homomorphism [math]\displaystyle{ \rho: G\to \text{GL}(V)=\text{Aut}(V). }[/math] Here [math]\displaystyle{ \text{GL}(V) }[/math] is notation for a general linear group, and [math]\displaystyle{ \text{Aut}(V) }[/math] for an automorphism group. This means that a linear representation is a map [math]\displaystyle{ \rho: G\to \text{GL}(V) }[/math] which satisfies [math]\displaystyle{ \rho(st)=\rho(s)\rho(t) }[/math] for all [math]\displaystyle{ s,t \in G. }[/math] The vector space [math]\displaystyle{ V }[/math] is called representation space of [math]\displaystyle{ G. }[/math] Often the term representation of [math]\displaystyle{ G }[/math] is also used for the representation space [math]\displaystyle{ V. }[/math]

The representation of a group in a module instead of a vector space is also called a linear representation.

We write [math]\displaystyle{ (\rho, V_\rho) }[/math] for the representation [math]\displaystyle{ \rho: G\to\text{GL}(V_\rho) }[/math] of [math]\displaystyle{ G. }[/math] Sometimes we use the notation [math]\displaystyle{ (\rho, V) }[/math] if it is clear to which representation the space [math]\displaystyle{ V }[/math] belongs.

In this article we will restrict ourselves to the study of finite-dimensional representation spaces, except for the last chapter. As in most cases only a finite number of vectors in [math]\displaystyle{ V }[/math] is of interest, it is sufficient to study the subrepresentation generated by these vectors. The representation space of this subrepresentation is then finite-dimensional.

The degree of a representation is the dimension of its representation space [math]\displaystyle{ V. }[/math] The notation [math]\displaystyle{ \dim (\rho) }[/math] is sometimes used to denote the degree of a representation [math]\displaystyle{ \rho. }[/math]

Examples

The trivial representation is given by [math]\displaystyle{ \rho(s)=\text{Id} }[/math] for all [math]\displaystyle{ s\in G. }[/math]

A representation of degree [math]\displaystyle{ 1 }[/math] of a group [math]\displaystyle{ G }[/math] is a homomorphism into the multiplicative group [math]\displaystyle{ \rho:G\to \text{GL}_1 (\Complex)=\Complex^\times = \Complex \setminus\{0\}. }[/math] As every element of [math]\displaystyle{ G }[/math] is of finite order, the values of [math]\displaystyle{ \rho(s) }[/math] are roots of unity. For example, let [math]\displaystyle{ \rho: G=\Z/4\Z \to \Complex ^\times }[/math] be a nontrivial linear representation. Since [math]\displaystyle{ \rho }[/math] is a group homomorphism, it has to satisfy [math]\displaystyle{ \rho({0})=1. }[/math] Because [math]\displaystyle{ 1 }[/math] generates [math]\displaystyle{ G, \rho }[/math] is determined by its value on [math]\displaystyle{ \rho(1). }[/math] And as [math]\displaystyle{ \rho }[/math] is nontrivial, [math]\displaystyle{ \rho({1})\in\{i,-1,-i\}. }[/math] Thus, we achieve the result that the image of [math]\displaystyle{ G }[/math] under [math]\displaystyle{ \rho }[/math] has to be a nontrivial subgroup of the group which consists of the fourth roots of unity. In other words, [math]\displaystyle{ \rho }[/math] has to be one of the following three maps:

[math]\displaystyle{ \begin{cases} \rho_1({0})=1 \\ \rho_1({1})=i \\ \rho_1({2})=-1 \\ \rho_1({3})=-i \end{cases} \qquad \begin{cases} \rho_2({0})=1 \\ \rho_2({1})=-1 \\ \rho_2({2})=1 \\ \rho_2({3})=-1 \end{cases} \qquad \begin{cases} \rho_3({0})=1 \\ \rho_3({1})=-i \\ \rho_3({2})=-1 \\ \rho_3({3})=i \end{cases} }[/math]

Let [math]\displaystyle{ G=\Z /2\Z \times\Z /2\Z }[/math] and let [math]\displaystyle{ \rho: G\to\text{GL}_2(\Complex ) }[/math] be the group homomorphism defined by:

[math]\displaystyle{ \rho({0},{0})= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \quad \rho({1},{0})= \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}, \quad \rho({0},{1})= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad \rho({1},{1})= \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix}. }[/math]

In this case [math]\displaystyle{ \rho }[/math] is a linear representation of [math]\displaystyle{ G }[/math] of degree [math]\displaystyle{ 2. }[/math]

Permutation representation

Further information: Permutation group

Let [math]\displaystyle{ X }[/math] be a finite set and let [math]\displaystyle{ G }[/math] be a group acting on [math]\displaystyle{ X. }[/math] Denote by [math]\displaystyle{ \text{Aut}(X) }[/math] the group of all permutations on [math]\displaystyle{ X }[/math] with the composition as group multiplication.

A group acting on a finite set is sometimes considered sufficient for the definition of the permutation representation. However, since we want to construct examples for linear representations - where groups act on vector spaces instead of on arbitrary finite sets - we have to proceed in a different way. In order to construct the permutation representation, we need a vector space [math]\displaystyle{ V }[/math] with [math]\displaystyle{ \dim (V)=|X|. }[/math] A basis of [math]\displaystyle{ V }[/math] can be indexed by the elements of [math]\displaystyle{ X. }[/math] The permutation representation is the group homomorphism [math]\displaystyle{ \rho : G \to\text{GL}(V) }[/math] given by [math]\displaystyle{ \rho(s)e_x=e_{s.x} }[/math] for all [math]\displaystyle{ s\in G, x\in X. }[/math] All linear maps [math]\displaystyle{ \rho(s) }[/math] are uniquely defined by this property.

Example. Let [math]\displaystyle{ X=\{1,2,3\} }[/math] and [math]\displaystyle{ G=\text{Sym}(3). }[/math] Then [math]\displaystyle{ G }[/math] acts on [math]\displaystyle{ X }[/math] via [math]\displaystyle{ \text{Aut}(X)=G. }[/math] The associated linear representation is [math]\displaystyle{ \rho:G\to \text{GL}(V)\cong\text{GL}_3(\Complex ) }[/math] with [math]\displaystyle{ \rho(\sigma)e_x=e_{\sigma(x)} }[/math] for [math]\displaystyle{ \sigma\in G, x\in X. }[/math]

Left- and right-regular representation

Let [math]\displaystyle{ G }[/math] be a group and [math]\displaystyle{ V }[/math] be a vector space of dimension [math]\displaystyle{ |G| }[/math] with a basis [math]\displaystyle{ (e_t)_{t\in G} }[/math] indexed by the elements of [math]\displaystyle{ G. }[/math] The left-regular representation is a special case of the permutation representation by choosing [math]\displaystyle{ X=G. }[/math] This means [math]\displaystyle{ \rho(s)e_t=e_{st} }[/math] for all [math]\displaystyle{ s, t\in G. }[/math] Thus, the family [math]\displaystyle{ (\rho(s)e_1)_{s\in G} }[/math] of images of [math]\displaystyle{ e_1 }[/math] are a basis of [math]\displaystyle{ V. }[/math] The degree of the left-regular representation is equal to the order of the group.

The right-regular representation is defined on the same vector space with a similar homomorphism: [math]\displaystyle{ \rho(s)e_t=e_{ts^{-1}}. }[/math] In the same way as before [math]\displaystyle{ (\rho(s)e_1)_{s\in G} }[/math] is a basis of [math]\displaystyle{ V. }[/math] Just as in the case of the left-regular representation, the degree of the right-regular representation is equal to the order of [math]\displaystyle{ G. }[/math]

Both representations are isomorphic via [math]\displaystyle{ e_{s} \mapsto e_{s^{-1}}. }[/math] For this reason they are not always set apart, and often referred to as "the" regular representation.

A closer look provides the following result: A given linear representation [math]\displaystyle{ \rho:G\to\text{GL}(W) }[/math] is isomorphic to the left-regular representation if and only if there exists a [math]\displaystyle{ w\in W, }[/math] such that [math]\displaystyle{ (\rho(s)w)_{s\in G} }[/math] is a basis of [math]\displaystyle{ W. }[/math]

Example. Let [math]\displaystyle{ G = \Z /5\Z }[/math] and [math]\displaystyle{ V=\R^5 }[/math] with the basis [math]\displaystyle{ \{e_0,\ldots, e_4\}. }[/math] Then the left-regular representation [math]\displaystyle{ L_\rho: G\to \text{GL}(V) }[/math] is defined by [math]\displaystyle{ L_\rho(k)e_l=e_{l+k} }[/math] for [math]\displaystyle{ k, l \in \Z /5\Z. }[/math] The right-regular representation is defined analogously by [math]\displaystyle{ R_\rho(k)e_l=e_{l-k} }[/math] for [math]\displaystyle{ k, l \in \Z /5\Z . }[/math]

Representations, modules and the convolution algebra

Let [math]\displaystyle{ G }[/math] be a finite group, let [math]\displaystyle{ K }[/math] be a commutative ring and let [math]\displaystyle{ K[G] }[/math] be the group algebra of [math]\displaystyle{ G }[/math] over [math]\displaystyle{ K. }[/math] This algebra is free and a basis can be indexed by the elements of [math]\displaystyle{ G. }[/math] Most often the basis is identified with [math]\displaystyle{ G }[/math]. Every element [math]\displaystyle{ f \in K[G] }[/math] can then be uniquely expressed as

[math]\displaystyle{ f=\sum_{s\in G} a_s s }[/math] with [math]\displaystyle{ a_s \in K }[/math].

The multiplication in [math]\displaystyle{ K[G] }[/math] extends that in [math]\displaystyle{ G }[/math] distributively.

Now let [math]\displaystyle{ V }[/math] be a [math]\displaystyle{ K }[/math]–module and let [math]\displaystyle{ \rho: G\to\text{GL}(V) }[/math] be a linear representation of [math]\displaystyle{ G }[/math] in [math]\displaystyle{ V. }[/math] We define [math]\displaystyle{ sv=\rho(s) v }[/math] for all [math]\displaystyle{ s\in G }[/math] and [math]\displaystyle{ v\in V }[/math]. By linear extension [math]\displaystyle{ V }[/math] is endowed with the structure of a left-[math]\displaystyle{ K[G] }[/math]–module. Vice versa we obtain a linear representation of [math]\displaystyle{ G }[/math] starting from a [math]\displaystyle{ K[G] }[/math]–module [math]\displaystyle{ V }[/math]. Additionally, homomorphisms of representations are in bijective correspondence with group algebra homomorphisms. Therefore, these terms may be used interchangeably. This is an example of an isomorphism of categories.

Suppose [math]\displaystyle{ K=\Complex. }[/math] In this case the left [math]\displaystyle{ \Complex [G] }[/math]–module given by [math]\displaystyle{ \Complex [G] }[/math] itself corresponds to the left-regular representation. In the same way [math]\displaystyle{ \Complex [G] }[/math] as a right [math]\displaystyle{ \Complex [G] }[/math]–module corresponds to the right-regular representation.

In the following we will define the convolution algebra: Let [math]\displaystyle{ G }[/math] be a group, the set [math]\displaystyle{ L^1(G):=\{f:G\to\Complex \} }[/math] is a [math]\displaystyle{ \Complex }[/math]–vector space with the operations addition and scalar multiplication then this vector space is isomorphic to [math]\displaystyle{ \Complex^{|G|}. }[/math] The convolution of two elements [math]\displaystyle{ f, h \in L^1(G) }[/math] defined by

[math]\displaystyle{ f*h(s):=\sum_{t\in G}f(t)h(t^{-1}s) }[/math]

makes [math]\displaystyle{ L^1(G) }[/math] an algebra. The algebra [math]\displaystyle{ L^1(G) }[/math] is called the convolution algebra.

The convolution algebra is free and has a basis indexed by the group elements: [math]\displaystyle{ (\delta_s)_{s\in G}, }[/math] where

[math]\displaystyle{ \delta_s(t)=\begin{cases} 1& t=s\\ 0 & \text{otherwise.}\end{cases} }[/math]

Using the properties of the convolution we obtain: [math]\displaystyle{ \delta_s*\delta_t=\delta_{st}. }[/math]

We define a map between [math]\displaystyle{ L^1(G) }[/math] and [math]\displaystyle{ \Complex [G], }[/math] by defining [math]\displaystyle{ \delta_s\mapsto e_s }[/math] on the basis [math]\displaystyle{ (\delta_s)_{s\in G} }[/math] and extending it linearly. Obviously the prior map is bijective. A closer inspection of the convolution of two basis elements as shown in the equation above reveals that the multiplication in [math]\displaystyle{ L^1(G) }[/math] corresponds to that in [math]\displaystyle{ \Complex [G]. }[/math] Thus, the convolution algebra and the group algebra are isomorphic as algebras.

The involution

[math]\displaystyle{ f^*(s)=\overline{f(s^{-1})} }[/math]

turns [math]\displaystyle{ L^1(G) }[/math] into a [math]\displaystyle{ ^* }[/math]–algebra. We have [math]\displaystyle{ \delta_s^*=\delta_{s^{-1}}. }[/math]

A representation [math]\displaystyle{ (\pi, V_\pi) }[/math] of a group [math]\displaystyle{ G }[/math] extends to a [math]\displaystyle{ ^* }[/math]–algebra homomorphism [math]\displaystyle{ \pi: L^1(G)\to\text{End}(V_\pi) }[/math] by [math]\displaystyle{ \pi(\delta_s)=\pi(s). }[/math] Since multiplicity is a characteristic property of algebra homomorphisms, [math]\displaystyle{ \pi }[/math] satisfies [math]\displaystyle{ \pi(f*h)=\pi(f)\pi(h). }[/math] If [math]\displaystyle{ \pi }[/math] is unitary, we also obtain [math]\displaystyle{ \pi(f)^* =\pi(f^*). }[/math] For the definition of a unitary representation, please refer to the chapter on properties. In that chapter we will see that (without loss of generality) every linear representation can be assumed to be unitary.

Using the convolution algebra we can implement a Fourier transformation on a group [math]\displaystyle{ G. }[/math] In the area of harmonic analysis it is shown that the following definition is consistent with the definition of the Fourier transformation on [math]\displaystyle{ \R. }[/math]

Let [math]\displaystyle{ \rho:G\to\text{GL}(V_\rho) }[/math] be a representation and let [math]\displaystyle{ f\in L^1(G) }[/math] be a [math]\displaystyle{ \Complex }[/math]-valued function on [math]\displaystyle{ G }[/math]. The Fourier transform [math]\displaystyle{ \hat{f}(\rho)\in \text{End}(V_\rho) }[/math] of [math]\displaystyle{ f }[/math] is defined as

[math]\displaystyle{ \hat{f}(\rho)=\sum_{s\in G} f(s)\rho(s). }[/math]

This transformation satisfies [math]\displaystyle{ \widehat{f*g}(\rho)=\hat{f}(\rho)\cdot\hat{g}(\rho). }[/math]

Maps between representations

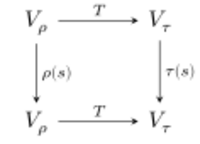
A map between two representations [math]\displaystyle{ (\rho, V_\rho),\, (\tau, V_\tau) }[/math] of the same group [math]\displaystyle{ G }[/math] is a linear map [math]\displaystyle{ T: V_\rho\to V_\tau, }[/math] with the property that [math]\displaystyle{ \tau(s)\circ T=T\circ\rho(s) }[/math] holds for all [math]\displaystyle{ s\in G. }[/math] In other words, the following diagram commutes for all [math]\displaystyle{ s\in G }[/math]:

Such a map is also called [math]\displaystyle{ G }[/math]–linear, or an equivariant map. The kernel, the image and the cokernel of [math]\displaystyle{ T }[/math] are defined by default. The composition of equivariant maps is again an equivariant map. There is a category of representations with equivariant maps as its morphisms. They are again [math]\displaystyle{ G }[/math]–modules. Thus, they provide representations of [math]\displaystyle{ G }[/math] due to the correlation described in the previous section.

Irreducible representations and Schur's lemma

Let [math]\displaystyle{ \rho:G\to\text{GL}(V) }[/math] be a linear representation of [math]\displaystyle{ G. }[/math] Let [math]\displaystyle{ W }[/math] be a [math]\displaystyle{ G }[/math]-invariant subspace of [math]\displaystyle{ V, }[/math] that is, [math]\displaystyle{ \rho(s)w\in W }[/math] for all [math]\displaystyle{ s\in G }[/math] and [math]\displaystyle{ w\in W }[/math]. The restriction [math]\displaystyle{ \rho(s)|_W }[/math] is an isomorphism of [math]\displaystyle{ W }[/math] onto itself. Because [math]\displaystyle{ \rho(s) |_W\circ\rho(t)|_W = \rho(st)|_W }[/math] holds for all [math]\displaystyle{ s,t\in G, }[/math] this construction is a representation of [math]\displaystyle{ G }[/math] in [math]\displaystyle{ W. }[/math] It is called subrepresentation of [math]\displaystyle{ V. }[/math] Any representation V has at least two subrepresentations, namely the one consisting only of 0, and the one consisting of V itself. The representation is called an irreducible representation, if these two are the only subrepresentations. Some authors also call these representations simple, given that they are precisely the simple modules over the group algebra [math]\displaystyle{ \Complex [G] }[/math].

Schur's lemma puts a strong constraint on maps between irreducible representations. If [math]\displaystyle{ \rho_1:G\to\text{GL}(V_1) }[/math] and [math]\displaystyle{ \rho_2:G\to\text{GL}(V_2) }[/math] are both irreducible, and [math]\displaystyle{ F: V_1\to V_2 }[/math] is a linear map such that [math]\displaystyle{ \rho_2(s)\circ F= F\circ \rho_1(s) }[/math] for all [math]\displaystyle{ s\in G. }[/math], there is the following dichotomy:

• If [math]\displaystyle{ V_1 = V_2 }[/math] and [math]\displaystyle{ \rho_1 = \rho_2, }[/math] [math]\displaystyle{ F }[/math] is a homothety (i.e. [math]\displaystyle{ F=\lambda\text{Id} }[/math] for a [math]\displaystyle{ \lambda \in \Complex }[/math]). More generally, if [math]\displaystyle{ \rho_1 }[/math] and [math]\displaystyle{ \rho_2 }[/math] are isomorphic, the space of G-linear maps is one-dimensional.
• Otherwise, if the two representations are not isomorphic, F must be 0.

Properties

Two representations [math]\displaystyle{ (\rho, V_{\rho}), (\pi, V_{\pi}) }[/math] are called equivalent or isomorphic, if there exists a [math]\displaystyle{ G }[/math]–linear vector space isomorphism between the representation spaces. In other words, they are isomorphic if there exists a bijective linear map [math]\displaystyle{ T: V_{\rho} \to V_{\pi}, }[/math] such that [math]\displaystyle{ T \circ \rho(s)=\pi(s)\circ T }[/math] for all [math]\displaystyle{ s \in G. }[/math] In particular, equivalent representations have the same degree.

A representation [math]\displaystyle{ (\pi,V_\pi) }[/math] is called faithful when [math]\displaystyle{ \pi }[/math] is injective. In this case [math]\displaystyle{ \pi }[/math] induces an isomorphism between [math]\displaystyle{ G }[/math] and the image [math]\displaystyle{ \pi(G). }[/math] As the latter is a subgroup of [math]\displaystyle{ \text{GL}(V_\pi), }[/math] we can regard [math]\displaystyle{ G }[/math] via [math]\displaystyle{ \pi }[/math] as subgroup of [math]\displaystyle{ \text{Aut}(V_\pi). }[/math]

We can restrict the range as well as the domain:

Let [math]\displaystyle{ H }[/math] be a subgroup of [math]\displaystyle{ G. }[/math] Let [math]\displaystyle{ \rho }[/math] be a linear representation of [math]\displaystyle{ G. }[/math] We denote by [math]\displaystyle{ \text{Res}_H(\rho) }[/math] the restriction of [math]\displaystyle{ \rho }[/math] to the subgroup [math]\displaystyle{ H. }[/math]

If there is no danger of confusion, we might use only [math]\displaystyle{ \text{Res}(\rho) }[/math] or in short [math]\displaystyle{ \text{Res}\rho. }[/math]

The notation [math]\displaystyle{ \text{Res}_H(V) }[/math] or in short [math]\displaystyle{ \text{Res}(V) }[/math] is also used to denote the restriction of the representation [math]\displaystyle{ V }[/math] of [math]\displaystyle{ G }[/math] onto [math]\displaystyle{ H. }[/math]

Let [math]\displaystyle{ f }[/math] be a function on [math]\displaystyle{ G. }[/math] We write [math]\displaystyle{ \text{Res}_H(f) }[/math] or shortly [math]\displaystyle{ \text{Res}(f) }[/math] for the restriction to the subgroup [math]\displaystyle{ H. }[/math]

It can be proven that the number of irreducible representations of a group [math]\displaystyle{ G }[/math] (or correspondingly the number of simple [math]\displaystyle{ \Complex [G] }[/math]–modules) equals the number of conjugacy classes of [math]\displaystyle{ G. }[/math]

A representation is called semisimple or completely reducible if it can be written as a direct sum of irreducible representations. This is analogous to the corresponding definition for a semisimple algebra.

For the definition of the direct sum of representations please refer to the section on direct sums of representations.

A representation is called isotypic if it is a direct sum of pairwise isomorphic irreducible representations.

Let [math]\displaystyle{ (\rho,V_\rho) }[/math] be a given representation of a group [math]\displaystyle{ G. }[/math] Let [math]\displaystyle{ \tau }[/math] be an irreducible representation of [math]\displaystyle{ G. }[/math] The [math]\displaystyle{ \tau }[/math]–isotype [math]\displaystyle{ V_\rho(\tau) }[/math] of [math]\displaystyle{ G }[/math] is defined as the sum of all irreducible subrepresentations of [math]\displaystyle{ V }[/math] isomorphic to [math]\displaystyle{ \tau. }[/math]

Every vector space over [math]\displaystyle{ \Complex }[/math] can be provided with an inner product. A representation [math]\displaystyle{ \rho }[/math] of a group [math]\displaystyle{ G }[/math] in a vector space endowed with an inner product is called unitary if [math]\displaystyle{ \rho(s) }[/math] is unitary for every [math]\displaystyle{ s\in G. }[/math] This means that in particular every [math]\displaystyle{ \rho(s) }[/math] is diagonalizable. For more details see the article on unitary representations.

A representation is unitary with respect to a given inner product if and only if the inner product is invariant with regard to the induced operation of [math]\displaystyle{ G, }[/math] i.e. if and only if [math]\displaystyle{ (v|u)=(\rho(s)v|\rho(s)u) }[/math] holds for all [math]\displaystyle{ v,u\in V_\rho, s\in G. }[/math]

A given inner product [math]\displaystyle{ (\cdot|\cdot) }[/math] can be replaced by an invariant inner product by exchanging [math]\displaystyle{ (v|u) }[/math] with

[math]\displaystyle{ \sum_{t\in G}(\rho(t)v|\rho(t)u). }[/math]

Thus, without loss of generality we can assume that every further considered representation is unitary.

Example. Let [math]\displaystyle{ G=D_6=\{\text{id},\mu,\mu^2,\nu,\mu\nu,\mu^2\nu\} }[/math] be the dihedral group of order [math]\displaystyle{ 6 }[/math] generated by [math]\displaystyle{ \mu,\nu }[/math] which fulfil the properties [math]\displaystyle{ \text{ord}(\nu)=2, \text{ord}(\mu)=3 }[/math] and [math]\displaystyle{ \nu\mu\nu=\mu^2. }[/math] Let [math]\displaystyle{ \rho:D_6\to\text{GL}_3(\Complex ) }[/math] be a linear representation of [math]\displaystyle{ D_6 }[/math] defined on the generators by:

[math]\displaystyle{ \rho(\mu)=\left( \begin{array}{ccc} \cos (\frac{2\pi}{3}) & 0& -\sin (\frac{2\pi}{3})\\ 0 & 1 & 0\\ \sin (\frac{2\pi}{3}) &0 & \cos (\frac{2\pi}{3}) \end{array} \right), \,\,\,\, \rho(\nu)= \left( \begin{array}{ccc} -1& 0&0\\ 0&-1&0\\ 0& 0 &1 \end{array} \right). }[/math]

This representation is faithful. The subspace [math]\displaystyle{ \Complex e_2 }[/math] is a [math]\displaystyle{ D_6 }[/math]–invariant subspace. Thus, there exists a nontrivial subrepresentation [math]\displaystyle{ \rho|_{\Complex e_2}: D_6\to\Complex ^\times }[/math] with [math]\displaystyle{ \nu\mapsto -1, \mu\mapsto 1. }[/math] Therefore, the representation is not irreducible. The mentioned subrepresentation is of degree one and irreducible. The complementary subspace of [math]\displaystyle{ \Complex e_2 }[/math] is [math]\displaystyle{ D_6 }[/math]–invariant as well. Therefore, we obtain the subrepresentation [math]\displaystyle{ \rho|_{\Complex e_1\oplus\Complex e_3} }[/math] with

[math]\displaystyle{ \nu \mapsto \begin{pmatrix} -1 &0 \\0&1 \end{pmatrix}, \,\,\,\,\mu \mapsto \begin{pmatrix} \cos (\frac{2\pi}{3}) &-\sin (\frac{2\pi}{3})\\\sin (\frac{2\pi}{3}) & \cos (\frac{2\pi}{3})\end{pmatrix}. }[/math]

This subrepresentation is also irreducible. That means, the original representation is completely reducible:

[math]\displaystyle{ \rho=\rho|_{\Complex e_2}\oplus \rho|_{\Complex e_1\oplus\Complex e_3}. }[/math]

Both subrepresentations are isotypic and are the two only non-zero isotypes of [math]\displaystyle{ \rho. }[/math]

The representation [math]\displaystyle{ \rho }[/math] is unitary with regard to the standard inner product on [math]\displaystyle{ \Complex ^3, }[/math] because [math]\displaystyle{ \rho(\mu) }[/math] and [math]\displaystyle{ \rho(\nu) }[/math] are unitary.

Let [math]\displaystyle{ T:\Complex ^3\to\Complex ^3 }[/math] be any vector space isomorphism. Then [math]\displaystyle{ \eta:D_6\to \text{GL}_3(\Complex ), }[/math] which is defined by the equation [math]\displaystyle{ \eta (s) :=T\circ\rho(s)\circ T^{-1} }[/math] for all [math]\displaystyle{ s\in D_6, }[/math] is a representation isomorphic to [math]\displaystyle{ \rho. }[/math]

By restricting the domain of the representation to a subgroup, e.g. [math]\displaystyle{ H=\{\text{id},\mu, \mu^2\}, }[/math] we obtain the representation [math]\displaystyle{ \text{Res}_H(\rho). }[/math] This representation is defined by the image [math]\displaystyle{ \rho(\mu), }[/math] whose explicit form is shown above.

Constructions

The dual representation

Let [math]\displaystyle{ \rho: G \to \text{GL}(V) }[/math] be a given representation. The dual representation or contragredient representation [math]\displaystyle{ \rho^*: G\to \text{GL}(V^*) }[/math] is a representation of [math]\displaystyle{ G }[/math] in the dual vector space of [math]\displaystyle{ V. }[/math] It is defined by the property

[math]\displaystyle{ \forall s\in G, v \in V, \alpha \in V^*: \qquad \left (\rho^*(s)\alpha \right )(v) =\alpha \left (\rho \left (s^{-1} \right ) v \right ). }[/math]

With regard to the natural pairing [math]\displaystyle{ \langle \alpha, v\rangle:=\alpha(v) }[/math] between [math]\displaystyle{ V^* }[/math] and [math]\displaystyle{ V }[/math] the definition above provides the equation:

[math]\displaystyle{ \forall s\in G, v \in V, \alpha \in V^*: \qquad \langle \rho^*(s)(\alpha), \rho(s)(v)\rangle = \langle \alpha,v \rangle. }[/math]

For an example, see the main page on this topic: Dual representation.

Direct sum of representations

Let [math]\displaystyle{ (\rho_1,V_1 ) }[/math] and [math]\displaystyle{ (\rho_2,V_2 ) }[/math] be a representation of [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2, }[/math] respectively. The direct sum of these representations is a linear representation and is defined as

[math]\displaystyle{ \forall s_1 \in G_1, s_2 \in G_2, v_1\in V_1, v_2\in V_2: \qquad \begin{cases} \rho_1\oplus\rho_2 : G_1\times G_2 \to \text{GL}(V_1 \oplus V_2 ) \\[4pt] (\rho_1\oplus\rho_2)(s_1, s_2) (v_1,v_2) := \rho_1(s_1)v_1\oplus \rho_2(s_2)v_2\end{cases} }[/math]

Let [math]\displaystyle{ \rho_1, \rho_2 }[/math] be representations of the same group [math]\displaystyle{ G. }[/math] For the sake of simplicity, the direct sum of these representations is defined as a representation of [math]\displaystyle{ G, }[/math] i.e. it is given as [math]\displaystyle{ \rho_1\oplus\rho_2:G\to\text{GL}(V_1\oplus V_2), }[/math] by viewing [math]\displaystyle{ G }[/math] as the diagonal subgroup of [math]\displaystyle{ G\times G. }[/math]

Example. Let (here [math]\displaystyle{ i }[/math] and [math]\displaystyle{ \omega }[/math] are the imaginary unit and the primitive cube root of unity respectively):

[math]\displaystyle{ \begin{cases} \rho_1: \Z /2\Z \to \text{GL}_2(\Complex ) \\[4pt] \rho_1(1)=\begin{pmatrix} 0 & -i \\ i & 0\end{pmatrix}\end{cases} \qquad\qquad \begin{cases} \rho_2: \Z /3\Z \to \text{GL}_3(\Complex )\\[6pt] \rho_2(1) = \begin{pmatrix} 1 & 0 & \omega \\ 0 & \omega & 0\\ 0 & 0 & \omega^2 \end{pmatrix} \end{cases} }[/math]

Then

[math]\displaystyle{ \begin{cases} \rho_1\oplus \rho_2 : \Z /2\Z \times\Z /3\Z \to \text{GL} \left ( \Complex ^2\oplus\Complex ^3 \right ) \\[6pt] \left (\rho_1\oplus\rho_2 \right ) (k,l) = \begin{pmatrix} \rho_1(k)& 0 \\ 0 & \rho_2(l) \end{pmatrix} & k\in\Z /2\Z, l\in \Z /3\Z \end{cases} }[/math]

As it is sufficient to consider the image of the generating element, we find that

[math]\displaystyle{ (\rho_1\oplus\rho_2) (1,1) = \begin{pmatrix} 0 & -i & 0 & 0 & 0 \\ i & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & \omega\\ 0 & 0 &0 & \omega & 0\\ 0 & 0 & 0 & 0 & \omega^2 \end{pmatrix} }[/math]

Tensor product of representations

Let [math]\displaystyle{ \rho_1:G_1\to \text{GL}(V_1), \rho_2:G_2\to\text{GL}(V_2) }[/math] be linear representations. We define the linear representation [math]\displaystyle{ \rho_1\otimes\rho_2:G_1\times G_2 \to \text{GL}(V_1\otimes V_2) }[/math] into the tensor product of [math]\displaystyle{ V_1 }[/math] and [math]\displaystyle{ V_2 }[/math] by [math]\displaystyle{ \rho_1\otimes\rho_2(s_1,s_2)=\rho_1(s_1)\otimes \rho_2(s_2), }[/math] in which [math]\displaystyle{ s_1\in G_1, s_2\in G_2. }[/math] This representation is called outer tensor product of the representations [math]\displaystyle{ \rho_1 }[/math] and [math]\displaystyle{ \rho_2. }[/math] The existence and uniqueness is a consequence of the properties of the tensor product.

Example. We reexamine the example provided for the direct sum:

[math]\displaystyle{ \begin{cases} \rho_1: \Z /2\Z \to \text{GL}_2(\Complex ) \\[4pt] \rho_1(1)=\begin{pmatrix} 0 & -i \\ i & 0\end{pmatrix}\end{cases} \qquad\qquad \begin{cases} \rho_2: \Z /3\Z \to \text{GL}_3(\Complex )\\[6pt] \rho_2(1) = \begin{pmatrix} 1 & 0 & \omega \\ 0 & \omega & 0\\ 0 & 0 & \omega^2 \end{pmatrix} \end{cases} }[/math]

The outer tensor product

[math]\displaystyle{ \begin{cases} \rho_1\otimes\rho_2 :\Z /2\Z \times \Z /3\Z \to \text{GL}(\Complex ^2\otimes\Complex ^3) \\ (\rho_1 \otimes \rho_2) (k,l) = \rho_1(k)\otimes \rho_2(l) & k\in\Z /2\Z, l\in\Z /3\Z \end{cases} }[/math]

Using the standard basis of [math]\displaystyle{ \Complex ^2\otimes\Complex ^3\cong \Complex ^6 }[/math] we have the following for the generating element:

[math]\displaystyle{ \rho_1\otimes\rho_2(1,1) = \rho_1(1)\otimes \rho_2(1) = \begin{pmatrix} 0 & 0 & 0 & -i & 0 & -i\omega \\ 0 & 0 & 0 & 0 & -i\omega &0\\ 0 & 0 & 0 & 0 & 0 & -i\omega^2\\ i & 0 & i\omega & 0 & 0 & 0 \\ 0 & i\omega &0 & 0 & 0 & 0\\ 0 & 0 & i\omega^2 & 0 & 0 & 0\end{pmatrix} }[/math]

Remark. Note that the direct sum and the tensor products have different degrees and hence are different representations.

Let [math]\displaystyle{ \rho_1: G \to \text{GL}(V_1), \rho_2: G \to \text{GL}(V_2) }[/math] be two linear representations of the same group. Let [math]\displaystyle{ s }[/math] be an element of [math]\displaystyle{ G. }[/math] Then [math]\displaystyle{ \rho(s)\in\text{GL}(V_1\otimes V_2) }[/math] is defined by [math]\displaystyle{ \rho(s)(v_1\otimes v_2)=\rho_1(s)v_1\otimes \rho_2(s)v_2, }[/math] for [math]\displaystyle{ v_1\in V_1, v_2\in V_2, }[/math] and we write [math]\displaystyle{ \rho(s)=\rho_1(s) \otimes \rho_2(s). }[/math] Then the map [math]\displaystyle{ s\mapsto \rho(s) }[/math] defines a linear representation of [math]\displaystyle{ G, }[/math] which is also called tensor product of the given representations.

These two cases have to be strictly distinguished. The first case is a representation of the group product into the tensor product of the corresponding representation spaces. The second case is a representation of the group [math]\displaystyle{ G }[/math] into the tensor product of two representation spaces of this one group. But this last case can be viewed as a special case of the first one by focusing on the diagonal subgroup [math]\displaystyle{ G\times G. }[/math] This definition can be iterated a finite number of times.

Let [math]\displaystyle{ V }[/math] and [math]\displaystyle{ W }[/math] be representations of the group [math]\displaystyle{ G. }[/math] Then [math]\displaystyle{ \text{Hom}(V,W) }[/math] is a representation by virtue of the following identity: [math]\displaystyle{ \text{Hom}(V,W)=V^*\otimes W }[/math]. Let [math]\displaystyle{ B \in \text{Hom}(V,W) }[/math] and let [math]\displaystyle{ \rho }[/math] be the representation on [math]\displaystyle{ \text{Hom}(V,W). }[/math] Let [math]\displaystyle{ \rho_V }[/math] be the representation on [math]\displaystyle{ V }[/math] and [math]\displaystyle{ \rho_W }[/math] the representation on [math]\displaystyle{ W. }[/math] Then the identity above leads to the following result:

[math]\displaystyle{ \rho(s)(B) v=\rho_W(s)\circ B \circ\rho_V(s^{-1})v }[/math] for all [math]\displaystyle{ s\in G, v\in V. }[/math]

Theorem. The irreducible representations of [math]\displaystyle{ G_1\times G_2 }[/math] up to isomorphism are exactly the representations [math]\displaystyle{ \rho_1\otimes\rho_2 }[/math] in which [math]\displaystyle{ \rho_1 }[/math] and [math]\displaystyle{ \rho_2 }[/math] are irreducible representations of [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2, }[/math] respectively.

Symmetric and alternating square

Let [math]\displaystyle{ \rho: G\to V\otimes V }[/math] be a linear representation of [math]\displaystyle{ G. }[/math] Let [math]\displaystyle{ (e_k) }[/math] be a basis of [math]\displaystyle{ V. }[/math] Define [math]\displaystyle{ \vartheta: V\otimes V \to V \otimes V }[/math] by extending [math]\displaystyle{ \vartheta(e_k\otimes e_j) =e_j \otimes e_k }[/math] linearly. It then holds that [math]\displaystyle{ \vartheta^2 =1 }[/math] and therefore [math]\displaystyle{ V\otimes V }[/math] splits up into [math]\displaystyle{ V\otimes V=\text{Sym}^2(V)\oplus \text{Alt}^2(V), }[/math] in which

[math]\displaystyle{ \text{Sym}^2(V) = \{z\in V\otimes V: \vartheta(z)=z \} }[/math]

[math]\displaystyle{ \text{Alt}^2(V)=\bigwedge^2V=\{z\in V\otimes V: \vartheta (z)=-z \}. }[/math]

These subspaces are [math]\displaystyle{ G }[/math]–invariant and by this define subrepresentations which are called the symmetric square and the alternating square, respectively. These subrepresentations are also defined in [math]\displaystyle{ V^{\otimes m}, }[/math] although in this case they are denoted wedge product [math]\displaystyle{ \bigwedge^m V }[/math] and symmetric product [math]\displaystyle{ \text{Sym}^m(V). }[/math] In case that [math]\displaystyle{ m\gt 2, }[/math] the vector space [math]\displaystyle{ V^{\otimes m} }[/math] is in general not equal to the direct sum of these two products.

Decompositions

In order to understand representations more easily, a decomposition of the representation space into the direct sum of simpler subrepresentations would be desirable. This can be achieved for finite groups as we will see in the following results. More detailed explanations and proofs may be found in [1] and [2].

Theorem. (Maschke) Let [math]\displaystyle{ \rho:G\to \text{GL}(V) }[/math] be a linear representation where [math]\displaystyle{ V }[/math] is a vector space over a field of characteristic zero. Let [math]\displaystyle{ W }[/math] be a [math]\displaystyle{ G }[/math]-invariant subspace of [math]\displaystyle{ V. }[/math] Then the complement [math]\displaystyle{ W^0 }[/math] of [math]\displaystyle{ W }[/math] exists in [math]\displaystyle{ V }[/math] and is [math]\displaystyle{ G }[/math]-invariant.

A subrepresentation and its complement determine a representation uniquely.

The following theorem will be presented in a more general way, as it provides a very beautiful result about representations of compact – and therefore also of finite – groups:

Theorem. Every linear representation of a compact group over a field of characteristic zero is a direct sum of irreducible representations.

Or in the language of [math]\displaystyle{ K[G] }[/math]-modules: If [math]\displaystyle{ \text{char}(K)=0, }[/math] the group algebra [math]\displaystyle{ K[G] }[/math] is semisimple, i.e. it is the direct sum of simple algebras.

Note that this decomposition is not unique. However, the number of how many times a subrepresentation isomorphic to a given irreducible representation is occurring in this decomposition is independent of the choice of decomposition.

The canonical decomposition

To achieve a unique decomposition, one has to combine all the irreducible subrepresentations that are isomorphic to each other. That means, the representation space is decomposed into a direct sum of its isotypes. This decomposition is uniquely determined. It is called the canonical decomposition.

Let [math]\displaystyle{ (\tau_j)_{j\in I} }[/math] be the set of all irreducible representations of a group [math]\displaystyle{ G }[/math] up to isomorphism. Let [math]\displaystyle{ V }[/math] be a representation of [math]\displaystyle{ G }[/math] and let [math]\displaystyle{ \{V(\tau_j)|j\in I\} }[/math] be the set of all isotypes of [math]\displaystyle{ V. }[/math] The projection [math]\displaystyle{ p_j:V\to V(\tau_j) }[/math] corresponding to the canonical decomposition is given by

[math]\displaystyle{ p_j=\frac{n_j}{g}\sum_{t\in G}\overline{\chi_{\tau_j}(t)}\rho(t), }[/math]

where [math]\displaystyle{ n_j=\dim (\tau_j), }[/math] [math]\displaystyle{ g=\text{ord}(G) }[/math] and [math]\displaystyle{ \chi_{\tau_j} }[/math] is the character belonging to [math]\displaystyle{ \tau_j. }[/math]

In the following, we show how to determine the isotype to the trivial representation:

Definition (Projection formula). For every representation [math]\displaystyle{ (\rho, V) }[/math] of a group [math]\displaystyle{ G }[/math] we define

[math]\displaystyle{ V^G:=\{v\in V : \rho(s)v=v\,\,\,\, \forall\, s \in G\}. }[/math]

In general, [math]\displaystyle{ \rho(s): V\to V }[/math] is not [math]\displaystyle{ G }[/math]-linear. We define

[math]\displaystyle{ P:= \frac{1}{|G|}\sum_{s\in G} \rho(s) \in \text{End}(V). }[/math]

Then [math]\displaystyle{ P }[/math] is a [math]\displaystyle{ G }[/math]-linear map, because

[math]\displaystyle{ \forall t \in G : \qquad \sum_{s\in G} \rho(s)= \sum_{s\in G} \rho(tst^{-1}). }[/math]

Proposition. The map [math]\displaystyle{ P }[/math] is a projection from [math]\displaystyle{ V }[/math] to [math]\displaystyle{ V^G. }[/math]

This proposition enables us to determine the isotype to the trivial subrepresentation of a given representation explicitly.

How often the trivial representation occurs in [math]\displaystyle{ V }[/math] is given by [math]\displaystyle{ \text{Tr}(P). }[/math] This result is a consequence of the fact that the eigenvalues of a projection are only [math]\displaystyle{ 0 }[/math] or [math]\displaystyle{ 1 }[/math] and that the eigenspace corresponding to the eigenvalue [math]\displaystyle{ 1 }[/math] is the image of the projection. Since the trace of the projection is the sum of all eigenvalues, we obtain the following result

[math]\displaystyle{ \dim(V(1))=\dim(V^G)=Tr(P)=\frac{1}{|G|}\sum_{s\in G}\chi_V(s), }[/math]

in which [math]\displaystyle{ V(1) }[/math] denotes the isotype of the trivial representation.

Let [math]\displaystyle{ V_\pi }[/math] be a nontrivial irreducible representation of [math]\displaystyle{ G. }[/math] Then the isotype to the trivial representation of [math]\displaystyle{ \pi }[/math] is the null space. That means the following equation holds

[math]\displaystyle{ P=\frac{1}{|G|}\sum_{s\in G} \pi(s)=0. }[/math]

Let [math]\displaystyle{ e_1,...,e_n }[/math] be an orthonormal basis of [math]\displaystyle{ V_\pi. }[/math] Then we have:

[math]\displaystyle{ \sum_{s\in G} \text{Tr}(\pi(s)) = \sum _{s\in G} \sum_{j=1}^{n} \langle \pi(s)e_j, e_j \rangle = \sum_{j=1}^{n} \left \langle \sum_{s\in G} \pi(s)e_j, e_j \right \rangle =0. }[/math]

Therefore, the following is valid for a nontrivial irreducible representation [math]\displaystyle{ V }[/math]:

[math]\displaystyle{ \sum_{s\in G} \chi_V(s)=0. }[/math]

Example. Let [math]\displaystyle{ G=\text{Per}(3) }[/math] be the permutation groups in three elements. Let [math]\displaystyle{ \rho: \text{Per}(3)\to \text{GL}_5(\Complex ) }[/math] be a linear representation of [math]\displaystyle{ \text{Per}(3) }[/math] defined on the generating elements as follows:

[math]\displaystyle{ \rho(1,2)= \begin{pmatrix} -1 & 2 & 0& 0& 0\\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0& 0 & 0 & 0 & 1 \end{pmatrix}, \quad \rho(1,3)= \begin{pmatrix} \frac{1}{2} & \frac{1}{2} & 0& 0& 0\\ \frac{1}{2} & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 0\\ 0& 0 & 1 & 0 & 0 \end{pmatrix}, \quad \rho(2,3)= \begin{pmatrix} 0 & -2 & 0& 0& 0\\ -\frac{1}{2} & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1\\ 0& 0 & 0 & 1 & 0 \end{pmatrix}. }[/math]

This representation can be decomposed on first look into the left-regular representation of [math]\displaystyle{ \text{Per}(3), }[/math]which is denoted by [math]\displaystyle{ \pi }[/math] in the following, and the representation [math]\displaystyle{ \eta: \text{Per}(3) \to \text{GL}_2(\Complex ) }[/math] with

[math]\displaystyle{ \eta(1,2)= \begin{pmatrix} -1 &2 \\ 0& 1\end{pmatrix}, \quad \eta(1,3)=\begin{pmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -1 \end{pmatrix},\quad \eta(2,3)= \begin{pmatrix}0& -2\\-\frac{1}{2} & 0\end{pmatrix}. }[/math]

With the help of the irreducibility criterion taken from the next chapter, we could realize that [math]\displaystyle{ \eta }[/math] is irreducible but [math]\displaystyle{ \pi }[/math] is not. This is because (in terms of the inner product from ”Inner product and characters” below) we have [math]\displaystyle{ (\eta|\eta)=1, (\pi|\pi)=2. }[/math]

The subspace [math]\displaystyle{ \Complex (e_1+e_2+e_3) }[/math] of [math]\displaystyle{ \Complex ^3 }[/math] is invariant with respect to the left-regular representation. Restricted to this subspace we obtain the trivial representation.

The orthogonal complement of [math]\displaystyle{ \Complex (e_1+e_2+e_3) }[/math] is [math]\displaystyle{ \Complex (e_1-e_2)\oplus\Complex (e_1+e_2-2e_3). }[/math] Restricted to this subspace, which is also [math]\displaystyle{ G }[/math]–invariant as we have seen above, we obtain the representation [math]\displaystyle{ \tau }[/math] given by

[math]\displaystyle{ \tau (1,2)= \begin{pmatrix} -1 &0 \\0 & 1\end{pmatrix},\quad \tau(1,3)=\begin{pmatrix}\frac{1}{2} & \frac{3}{2}\\ \frac{1}{2} & -\frac{1}{2}\end{pmatrix}, \quad \tau(2,3)=\begin{pmatrix} \frac{1}{2} & -\frac{3}{2}\\ -\frac{1}{2} & -\frac{1}{2}\end{pmatrix}. }[/math]

Again, we can use the irreducibility criterion of the next chapter to prove that [math]\displaystyle{ \tau }[/math] is irreducible. Now, [math]\displaystyle{ \eta }[/math] and [math]\displaystyle{ \tau }[/math] are isomorphic because [math]\displaystyle{ \eta(s)=B\circ\tau(s)\circ B^{-1} }[/math] for all [math]\displaystyle{ s\in \text{Per}(3), }[/math] in which [math]\displaystyle{ B:\Complex ^2\to\Complex ^2 }[/math] is given by the matrix

[math]\displaystyle{ M_B=\begin{pmatrix} 2 &2\\0&2\end{pmatrix}. }[/math]

A decomposition of [math]\displaystyle{ (\rho,\Complex ^5) }[/math] in irreducible subrepresentations is: [math]\displaystyle{ \rho=\tau\oplus\eta\oplus 1 }[/math] where [math]\displaystyle{ 1 }[/math] denotes the trivial representation and

[math]\displaystyle{ \Complex ^5=\Complex (e_1,e_2)\oplus\Complex (e_3-e_4, e_3+e_4-2e_5)\oplus\Complex (e_3+e_4+e_5) }[/math]

is the corresponding decomposition of the representation space.

We obtain the canonical decomposition by combining all the isomorphic irreducible subrepresentations: [math]\displaystyle{ \rho_1:=\eta\oplus\tau }[/math] is the [math]\displaystyle{ \tau }[/math]-isotype of [math]\displaystyle{ \rho }[/math] and consequently the canonical decomposition is given by

[math]\displaystyle{ \rho=\rho_1\oplus 1, \qquad \Complex ^5=\Complex (e_1,e_2,e_3-e_4, e_3+e_4-2e_5)\oplus\Complex (e_3+e_4+e_5). }[/math]

The theorems above are in general not valid for infinite groups. This will be demonstrated by the following example: let

[math]\displaystyle{ G=\{ A\in \text{GL}_2(\Complex )| \,A\,\, \text{ is an upper triangular matrix}\}. }[/math]

Together with the matrix multiplication [math]\displaystyle{ G }[/math] is an infinite group. [math]\displaystyle{ G }[/math] acts on [math]\displaystyle{ \Complex ^2 }[/math] by matrix-vector multiplication. We consider the representation [math]\displaystyle{ \rho(A)=A }[/math] for all [math]\displaystyle{ A\in G. }[/math] The subspace [math]\displaystyle{ \Complex e_1 }[/math] is a [math]\displaystyle{ G }[/math]-invariant subspace. However, there exists no [math]\displaystyle{ G }[/math]-invariant complement to this subspace. The assumption that such a complement exists would entail that every matrix is diagonalizable over [math]\displaystyle{ \Complex . }[/math] This is known to be wrong and thus yields a contradiction.

The moral of the story is that if we consider infinite groups, it is possible that a representation - even one that is not irreducible - can not be decomposed into a direct sum of irreducible subrepresentations.

Character theory

Definitions

The character of a representation [math]\displaystyle{ \rho: G\to \text{GL}(V) }[/math] is defined as the map

[math]\displaystyle{ \chi_\rho : G \to \Complex, \chi_\rho(s) := \text{Tr}(\rho(s)), }[/math] in which [math]\displaystyle{ \text{Tr}(\rho(s)) }[/math] denotes the trace of the linear map [math]\displaystyle{ \rho(s). }[/math]

Even though the character is a map between two groups, it is not in general a group homomorphism, as the following example shows.

Let [math]\displaystyle{ \rho: \Z /2\Z \times\Z /2\Z\to\text{GL}_2(\Complex ) }[/math] be the representation defined by:

[math]\displaystyle{ \rho(0,0)= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \quad \rho(1, 0)= \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}, \quad \rho(0,1)= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad \rho(1,1)= \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix}. }[/math]

The character [math]\displaystyle{ \chi_\rho }[/math] is given by

[math]\displaystyle{ \chi_\rho(0,0)=2, \quad \chi_\rho(1,0)=-2,\quad \chi_\rho(0,1)=\chi_\rho(1,1)=0. }[/math]

Characters of permutation representations are particularly easy to compute. If V is the G-representation corresponding to the left action of [math]\displaystyle{ G }[/math] on a finite set [math]\displaystyle{ X }[/math], then

[math]\displaystyle{ \chi_V(s)=|\{x\in X | s\cdot x=x\}|. }[/math]

For example, the character of the regular representation [math]\displaystyle{ R }[/math] is given by

[math]\displaystyle{ \chi_R(s)=\begin{cases} 0 & s\neq e\\ |G| & s=e\end{cases}, }[/math]

where [math]\displaystyle{ e }[/math] denotes the neutral element of [math]\displaystyle{ G. }[/math]

Properties

A crucial property of characters is the formula

[math]\displaystyle{ \chi(tst^{-1})=\chi(s),\,\,\forall\,s,t\in G. }[/math]

This formula follows from the fact that the trace of a product AB of two square matrices is the same as the trace of BA. Functions [math]\displaystyle{ G \to \Complex }[/math] satisfying such a formula are called class functions. Put differently, class functions and in particular characters are constant on each conjugacy class [math]\displaystyle{ C_s = \{tst^{-1}| t \in G \}. }[/math] It also follows from elementary properties of the trace that [math]\displaystyle{ \chi(s) }[/math] is the sum of the eigenvalues of [math]\displaystyle{ \rho(s) }[/math] with multiplicity. If the degree of the representation is n, then the sum is n long. If s has order m, these eigenvalues are all m-th roots of unity. This fact can be used to show that [math]\displaystyle{ \chi(s^{-1})=\overline{\chi(s)},\,\,\,\forall\, s\in G }[/math] and it also implies [math]\displaystyle{ |\chi(s)|\leqslant n. }[/math]

Since the trace of the identity matrix is the number of rows, [math]\displaystyle{ \chi(e)=n, }[/math] where [math]\displaystyle{ e }[/math] is the neutral element of [math]\displaystyle{ G }[/math] and n is the dimension of the representation. In general, [math]\displaystyle{ \{s\in G | \chi(s)=n\} }[/math] is a normal subgroup in [math]\displaystyle{ G. }[/math] The following table shows how the characters [math]\displaystyle{ \chi_1, \chi_2 }[/math] of two given representations [math]\displaystyle{ \rho_1:G\to \text{GL}(V_1), \rho_2:G \to \text{GL}(V_2) }[/math] give rise to characters of related representations.

Characters of several standard constructions

Representation	Character
dual representation [math]\displaystyle{ V_1^* }[/math]	[math]\displaystyle{ \chi_1^*=\overline{\chi_1}. }[/math]
direct sum [math]\displaystyle{ V_1\oplus V_2 }[/math]	[math]\displaystyle{ \chi_1 + \chi_2. }[/math]
tensor product of the representations [math]\displaystyle{ V_1\otimes V_2 }[/math]	[math]\displaystyle{ \chi_1\chi_2. }[/math]
symmetric square [math]\displaystyle{ Sym^2(V) }[/math]	[math]\displaystyle{ \tfrac{1}{2} \left (\chi(s)^2+\chi(s^2) \right ) }[/math]
alternating square [math]\displaystyle{ \bigwedge^2 V }[/math]	[math]\displaystyle{ \tfrac{1}{2} \left (\chi(s)^2 - \chi(s^2) \right ) }[/math]

By construction, there is a direct sum decomposition of [math]\displaystyle{ V \otimes V = Sym^2(V) \oplus \bigwedge^2 V }[/math]. On characters, this corresponds to the fact that the sum of the last two expressions in the table is [math]\displaystyle{ \chi(s)^2 }[/math], the character of [math]\displaystyle{ V \otimes V }[/math].

Inner product and characters

In order to show some particularly interesting results about characters, it is rewarding to consider a more general type of functions on groups:

Definition (Class functions). A function [math]\displaystyle{ \varphi : G \to \Complex }[/math] is called a class function if it is constant on conjugacy classes of [math]\displaystyle{ G }[/math], i.e.

[math]\displaystyle{ \forall s, t \in G : \quad \varphi \left (sts^{-1} \right ) =\varphi(t). }[/math]

Note that every character is a class function, as the trace of a matrix is preserved under conjugation.

The set of all class functions is a [math]\displaystyle{ \Complex }[/math]–algebra and is denoted by [math]\displaystyle{ \Complex _{\text{class}}(G) }[/math]. Its dimension is equal to the number of conjugacy classes of [math]\displaystyle{ G. }[/math]

Proofs of the following results of this chapter may be found in [1], [2] and [3].

An inner product can be defined on the set of all class functions on a finite group:

[math]\displaystyle{ (f|h)_G=\frac{1}{|G|} \sum_{t\in G}f(t)\overline{h(t)} }[/math]

Orthonormal property. If [math]\displaystyle{ \chi_1, \ldots ,\chi_k }[/math] are the distinct irreducible characters of [math]\displaystyle{ G }[/math], they form an orthonormal basis for the vector space of all class functions with respect to the inner product defined above, i.e.

• [math]\displaystyle{ (\chi_i|\chi_j)=\begin{cases} 1 \text{ if } i= j \\0 \text{ otherwise }\end{cases}. }[/math]
• Every class function [math]\displaystyle{ f }[/math] may be expressed as a unique linear combination of the irreducible characters [math]\displaystyle{ \chi_1, \ldots ,\chi_k }[/math].

One might verify that the irreducible characters generate [math]\displaystyle{ \Complex _{\text{class}}(G) }[/math] by showing that there exists no nonzero class function which is orthogonal to all the irreducible characters. For [math]\displaystyle{ \rho }[/math] a representation and [math]\displaystyle{ f }[/math] a class function, denote [math]\displaystyle{ \rho_f = \sum_g f(g)\rho (g). }[/math] Then for [math]\displaystyle{ \rho }[/math] irreducible, we have [math]\displaystyle{ \rho_f = \frac {|G|}{n} \langle f,\chi _V^{*} \rangle \in End(V) }[/math] from Schur's lemma. Suppose [math]\displaystyle{ f }[/math] is a class function which is orthogonal to all the characters. Then by the above we have [math]\displaystyle{ \rho _f = 0 }[/math] whenever [math]\displaystyle{ \rho }[/math] is irreducible. But then it follows that [math]\displaystyle{ \rho _f = 0 }[/math] for all [math]\displaystyle{ \rho }[/math], by decomposability. Take [math]\displaystyle{ \rho }[/math] to be the regular representation. Applying [math]\displaystyle{ \rho _f }[/math] to some particular basis element [math]\displaystyle{ g }[/math], we get [math]\displaystyle{ f(g)=0 }[/math]. Since this is true for all [math]\displaystyle{ g }[/math], we have [math]\displaystyle{ f=0. }[/math]

It follows from the orthonormal property that the number of non-isomorphic irreducible representations of a group [math]\displaystyle{ G }[/math] is equal to the number of conjugacy classes of [math]\displaystyle{ G. }[/math]

Furthermore, a class function on [math]\displaystyle{ G }[/math] is a character of [math]\displaystyle{ G }[/math] if and only if it can be written as a linear combination of the distinct irreducible characters [math]\displaystyle{ \chi_j }[/math] with non-negative integer coefficients: if [math]\displaystyle{ \varphi }[/math] is a class function on [math]\displaystyle{ G }[/math] such that [math]\displaystyle{ \varphi=c_1 \chi_1 + \cdots + c_k \chi_k }[/math] where [math]\displaystyle{ c_j }[/math] non-negative integers, then [math]\displaystyle{ \varphi }[/math] is the character of the direct sum [math]\displaystyle{ c_1 \tau_1 \oplus \cdots \oplus c_k \tau_k }[/math] of the representations [math]\displaystyle{ \tau_j }[/math] corresponding to [math]\displaystyle{ \chi_j. }[/math] Conversely, it is always possible to write any character as a sum of irreducible characters.

The inner product defined above can be extended on the set of all [math]\displaystyle{ \Complex }[/math]-valued functions [math]\displaystyle{ L^1(G) }[/math] on a finite group:

[math]\displaystyle{ (f|h)_G=\frac{1}{|G|} \sum_{t\in G}f(t)\overline{h(t)} }[/math]

A symmetric bilinear form can also be defined on [math]\displaystyle{ L^1(G): }[/math]

[math]\displaystyle{ \langle f,h\rangle_G=\frac{1}{|G|} \sum_{t\in G}f(t)h(t^{-1}) }[/math]

These two forms match on the set of characters. If there is no danger of confusion the index of both forms [math]\displaystyle{ (\cdot|\cdot)_G }[/math] and [math]\displaystyle{ \langle\cdot|\cdot\rangle_G }[/math] will be omitted.

Let [math]\displaystyle{ V_1, V_2 }[/math] be two [math]\displaystyle{ \Complex [G] }[/math]–modules. Note that [math]\displaystyle{ \Complex [G] }[/math]–modules are simply representations of [math]\displaystyle{ G }[/math]. Since the orthonormal property yields the number of irreducible representations of [math]\displaystyle{ G }[/math] is exactly the number of its conjugacy classes, then there are exactly as many simple [math]\displaystyle{ \Complex [G] }[/math]–modules (up to isomorphism) as there are conjugacy classes of [math]\displaystyle{ G. }[/math]

We define [math]\displaystyle{ \langle V_1, V_2 \rangle_G:=\dim (\text{Hom}^G(V_1,V_2)), }[/math] in which [math]\displaystyle{ \text{Hom}^G(V_1,V_2) }[/math] is the vector space of all [math]\displaystyle{ G }[/math]–linear maps. This form is bilinear with respect to the direct sum.

In the following, these bilinear forms will allow us to obtain some important results with respect to the decomposition and irreducibility of representations.

For instance, let [math]\displaystyle{ \chi_1 }[/math] and [math]\displaystyle{ \chi_2 }[/math] be the characters of [math]\displaystyle{ V_1 }[/math] and [math]\displaystyle{ V_2, }[/math] respectively. Then[math]\displaystyle{ \langle\chi_1,\chi_2\rangle_G = (\chi_1|\chi_2)_G=\langle V_1, V_2 \rangle_G. }[/math]

It is possible to derive the following theorem from the results above, along with Schur's lemma and the complete reducibility of representations.

Theorem. Let [math]\displaystyle{ V }[/math] be a linear representation of [math]\displaystyle{ G }[/math] with character [math]\displaystyle{ \xi. }[/math] Let [math]\displaystyle{ V=W_1\oplus \cdots \oplus W_k, }[/math] where [math]\displaystyle{ W_j }[/math] are irreducible. Let [math]\displaystyle{ (\tau,W) }[/math] be an irreducible representation of [math]\displaystyle{ G }[/math] with character [math]\displaystyle{ \chi. }[/math] Then the number of subrepresentations [math]\displaystyle{ W_j }[/math] which are isomorphic to [math]\displaystyle{ W }[/math] is independent of the given decomposition and is equal to the inner product [math]\displaystyle{ (\xi|\chi), }[/math] i.e. the [math]\displaystyle{ \tau }[/math]–isotype [math]\displaystyle{ V(\tau) }[/math] of [math]\displaystyle{ V }[/math] is independent of the choice of decomposition. We also get:

[math]\displaystyle{ (\xi|\chi)=\frac{\dim (V(\tau))}{\dim (\tau)}=\langle V, W\rangle }[/math]

and thus

[math]\displaystyle{ \dim (V(\tau))=\dim (\tau)(\xi|\chi). }[/math]

Corollary. Two representations with the same character are isomorphic. This means that every representation is determined by its character.

With this we obtain a very useful result to analyse representations:

Irreducibility criterion. Let [math]\displaystyle{ \chi }[/math] be the character of the representation [math]\displaystyle{ V, }[/math] then we have [math]\displaystyle{ (\chi|\chi) \in \mathbb{N}_0. }[/math] The case [math]\displaystyle{ (\chi|\chi)=1 }[/math] holds if and only if [math]\displaystyle{ V }[/math] is irreducible.

Therefore, using the first theorem, the characters of irreducible representations of [math]\displaystyle{ G }[/math] form an orthonormal set on [math]\displaystyle{ \Complex _{\text{class}}(G) }[/math] with respect to this inner product.

Corollary. Let [math]\displaystyle{ V }[/math] be a vector space with [math]\displaystyle{ \dim (V)=n. }[/math] A given irreducible representation [math]\displaystyle{ V }[/math] of [math]\displaystyle{ G }[/math] is contained [math]\displaystyle{ n }[/math]–times in the regular representation. In other words, if [math]\displaystyle{ R }[/math] denotes the regular representation of [math]\displaystyle{ G }[/math] then we have: [math]\displaystyle{ R \cong \oplus (W_j)^{\oplus\dim (W_j)}, }[/math] in which [math]\displaystyle{ \{W_j|j\in I\} }[/math] is the set of all irreducible representations of [math]\displaystyle{ G }[/math] that are pairwise not isomorphic to each other.

In terms of the group algebra, this means that [math]\displaystyle{ \Complex [G]\cong\oplus_{j}\text{End}(W_j) }[/math] as algebras.

As a numerical result we get:

[math]\displaystyle{ |G|=\chi_R(e)=\dim (R)=\sum_j\dim \left ((W_j)^{\oplus(\chi_{W_j}|\chi_R)} \right )=\sum_j(\chi_{W_j}|\chi_R)\cdot\dim (W_j)=\sum_j\dim (W_j)^2, }[/math]

in which [math]\displaystyle{ R }[/math] is the regular representation and [math]\displaystyle{ \chi_{W_j} }[/math] and [math]\displaystyle{ \chi_R }[/math] are corresponding characters to [math]\displaystyle{ W_j }[/math] and [math]\displaystyle{ R, }[/math] respectively. Recall that [math]\displaystyle{ e }[/math] denotes the neutral element of the group.

This formula is a "necessary and sufficient" condition for the problem of classifying the irreducible representations of a group up to isomorphism. It provides us with the means to check whether we found all the isomorphism classes of irreducible representations of a group.

Similarly, by using the character of the regular representation evaluated at [math]\displaystyle{ s\neq e, }[/math] we get the equation:

[math]\displaystyle{ 0=\chi_R(s)=\sum_j\dim (W_j)\cdot\chi_{W_j}(s). }[/math]

Using the description of representations via the convolution algebra we achieve an equivalent formulation of these equations:

The Fourier inversion formula:

[math]\displaystyle{ f(s)=\frac{1}{|G|}\sum_{\rho \text{ irr. rep. of } G}\dim (V_\rho)\cdot\text{Tr}(\rho(s^{-1})\cdot \hat{f}(\rho)). }[/math]

In addition, the Plancherel formula holds:

[math]\displaystyle{ \sum_{s\in G}f(s^{-1})h(s)=\frac{1}{|G|}\sum_{\rho\,\, \text{ irred.} \text{ rep.}\text{ of } G}\dim (V_{\rho})\cdot\text{Tr}(\hat{f}(\rho)\hat{h}(\rho)). }[/math]

In both formulas [math]\displaystyle{ (\rho, V_\rho) }[/math] is a linear representation of a group [math]\displaystyle{ G, s\in G }[/math] and [math]\displaystyle{ f, h \in L^1(G). }[/math]

The corollary above has an additional consequence:

Lemma. Let [math]\displaystyle{ G }[/math] be a group. Then the following is equivalent:

• [math]\displaystyle{ G }[/math] is abelian.
• Every function on [math]\displaystyle{ G }[/math] is a class function.
• All irreducible representations of [math]\displaystyle{ G }[/math] have degree [math]\displaystyle{ 1. }[/math]

The induced representation

As was shown in the section on properties of linear representations, we can - by restriction - obtain a representation of a subgroup starting from a representation of a group. Naturally we are interested in the reverse process: Is it possible to obtain the representation of a group starting from a representation of a subgroup? We will see that the induced representation defined below provides us with the necessary concept. Admittedly, this construction is not inverse but rather adjoint to the restriction.

Definitions

Let [math]\displaystyle{ \rho: G\to \text{GL}(V_\rho) }[/math] be a linear representation of [math]\displaystyle{ G. }[/math] Let [math]\displaystyle{ H }[/math] be a subgroup and [math]\displaystyle{ \rho|_H }[/math] the restriction. Let [math]\displaystyle{ W }[/math] be a subrepresentation of [math]\displaystyle{ \rho_H. }[/math] We write [math]\displaystyle{ \theta:H \to \text{GL}(W) }[/math] to denote this representation. Let [math]\displaystyle{ s\in G. }[/math] The vector space [math]\displaystyle{ \rho(s)(W) }[/math] depends only on the left coset [math]\displaystyle{ sH }[/math] of [math]\displaystyle{ s. }[/math] Let [math]\displaystyle{ R }[/math] be a representative system of [math]\displaystyle{ G/H, }[/math] then

[math]\displaystyle{ \sum_{r\in R} \rho(r)(W) }[/math]

is a subrepresentation of [math]\displaystyle{ V_\rho. }[/math]

A representation [math]\displaystyle{ \rho }[/math] of [math]\displaystyle{ G }[/math] in [math]\displaystyle{ V_\rho }[/math] is called induced by the representation [math]\displaystyle{ \theta }[/math] of [math]\displaystyle{ H }[/math] in [math]\displaystyle{ W, }[/math] if

[math]\displaystyle{ V_\rho= \bigoplus_{r\in R} W_r. }[/math]

Here [math]\displaystyle{ R }[/math] denotes a representative system of [math]\displaystyle{ G/H }[/math] and [math]\displaystyle{ W_r=\rho(s)(W) }[/math] for all [math]\displaystyle{ s\in rH }[/math] and for all [math]\displaystyle{ r\in R. }[/math] In other words: the representation [math]\displaystyle{ (\rho,V_\rho) }[/math] is induced by [math]\displaystyle{ (\theta, W), }[/math] if every [math]\displaystyle{ v\in V_\rho }[/math] can be written uniquely as

[math]\displaystyle{ \sum_{r\in R}w_r, }[/math]

where [math]\displaystyle{ w_r \in W_r }[/math] for every [math]\displaystyle{ r\in R. }[/math]

We denote the representation [math]\displaystyle{ \rho }[/math] of [math]\displaystyle{ G }[/math] which is induced by the representation [math]\displaystyle{ \theta }[/math] of [math]\displaystyle{ H }[/math] as [math]\displaystyle{ \rho=\text{Ind}^G_H(\theta), }[/math] or in short [math]\displaystyle{ \rho=\text{Ind}(\theta), }[/math] if there is no danger of confusion. The representation space itself is frequently used instead of the representation map, i.e. [math]\displaystyle{ V=\text{Ind}^G_H(W), }[/math] or [math]\displaystyle{ V=\text{Ind}(W), }[/math] if the representation [math]\displaystyle{ V }[/math] is induced by [math]\displaystyle{ W. }[/math]

Alternative description of the induced representation

By using the group algebra we obtain an alternative description of the induced representation:

Let [math]\displaystyle{ G }[/math] be a group, [math]\displaystyle{ V }[/math] a [math]\displaystyle{ \Complex [G] }[/math]–module and [math]\displaystyle{ W }[/math] a [math]\displaystyle{ \Complex [H] }[/math]–submodule of [math]\displaystyle{ V }[/math] corresponding to the subgroup [math]\displaystyle{ H }[/math] of [math]\displaystyle{ G. }[/math] We say that [math]\displaystyle{ V }[/math] is induced by [math]\displaystyle{ W }[/math] if [math]\displaystyle{ V= \Complex[G]\otimes_{\Complex[H]}W, }[/math] in which [math]\displaystyle{ G }[/math] acts on the first factor: [math]\displaystyle{ s\cdot (e_t \otimes w)=e_{st}\otimes w }[/math] for all [math]\displaystyle{ s,t\in G, w\in W. }[/math]

Properties

The results introduced in this section will be presented without proof. These may be found in [1] and [2].

Uniqueness and existence of the induced representation. Let [math]\displaystyle{ (\theta, W_\theta) }[/math] be a linear representation of a subgroup [math]\displaystyle{ H }[/math] of [math]\displaystyle{ G. }[/math] Then there exists a linear representation [math]\displaystyle{ (\rho, V_\rho) }[/math] of [math]\displaystyle{ G, }[/math] which is induced by [math]\displaystyle{ (\theta, W_\theta). }[/math] Note that this representation is unique up to isomorphism.

Transitivity of induction. Let [math]\displaystyle{ W }[/math] be a representation of [math]\displaystyle{ H }[/math] and let [math]\displaystyle{ H \leq G \leq K }[/math] be an ascending series of groups. Then we have

[math]\displaystyle{ \text{Ind}^K_G(\text{Ind}^G_H(W))\cong\text{Ind}^K_H(W). }[/math]

Lemma. Let [math]\displaystyle{ (\rho, V_\rho) }[/math] be induced by [math]\displaystyle{ (\theta,W_\theta) }[/math] and let [math]\displaystyle{ \rho':G\to\text{GL}(V') }[/math] be a linear representation of [math]\displaystyle{ G. }[/math] Now let [math]\displaystyle{ F: W_\theta\to V' }[/math] be a linear map satisfying the property that [math]\displaystyle{ F\circ\theta(t)=\rho'(t)\circ F }[/math] for all [math]\displaystyle{ t\in G. }[/math] Then there exists a uniquely determined linear map [math]\displaystyle{ F':V_\rho\to V', }[/math] which extends [math]\displaystyle{ F }[/math] and for which [math]\displaystyle{ F'\circ\rho(s)=\rho'(s)\circ F' }[/math] is valid for all [math]\displaystyle{ s\in G. }[/math]

This means that if we interpret [math]\displaystyle{ V' }[/math] as a [math]\displaystyle{ \Complex[G] }[/math]–module, we have [math]\displaystyle{ \text{Hom}^H(W_\theta,V') \cong \text{Hom}^G(V_\rho,V'), }[/math] where [math]\displaystyle{ \text{Hom}^G(V_\rho,V') }[/math] is the vector space of all [math]\displaystyle{ \Complex[G] }[/math]–homomorphisms of [math]\displaystyle{ V_\rho }[/math] to [math]\displaystyle{ V'. }[/math] The same is valid for [math]\displaystyle{ \text{Hom}^H(W_\theta,V'). }[/math]

Induction on class functions. In the same way as it was done with representations, we can - by induction - obtain a class function on the group from a class function on a subgroup. Let [math]\displaystyle{ \varphi }[/math] be a class function on [math]\displaystyle{ H. }[/math] We define a function [math]\displaystyle{ \varphi' }[/math] on [math]\displaystyle{ G }[/math] by

[math]\displaystyle{ \varphi'(s)=\frac{1}{|H|}\sum_{t\in G\atop t^{-1}st\in H}^{}\varphi(t^{-1}st). }[/math]

We say [math]\displaystyle{ \varphi' }[/math] is induced by [math]\displaystyle{ \varphi }[/math] and write [math]\displaystyle{ \text{Ind}^G_H(\varphi)=\varphi' }[/math] or [math]\displaystyle{ \text{Ind}(\varphi)=\varphi'. }[/math]

Proposition. The function [math]\displaystyle{ \text{Ind}(\varphi) }[/math] is a class function on [math]\displaystyle{ G. }[/math] If [math]\displaystyle{ \varphi }[/math] is the character of a representation [math]\displaystyle{ W }[/math] of [math]\displaystyle{ H, }[/math] then [math]\displaystyle{ \text{Ind}(\varphi) }[/math] is the character of the induced representation [math]\displaystyle{ \text{Ind}(W) }[/math] of [math]\displaystyle{ G. }[/math]

Lemma. If [math]\displaystyle{ \psi }[/math] is a class function on [math]\displaystyle{ H }[/math] and [math]\displaystyle{ \varphi }[/math] is a class function on [math]\displaystyle{ G, }[/math] then we have: [math]\displaystyle{ \text{Ind}(\psi \cdot \text{Res}\varphi) = (\text{Ind} \psi) \cdot \varphi. }[/math]

Theorem. Let [math]\displaystyle{ (\rho,V_\rho) }[/math] be the representation of [math]\displaystyle{ G }[/math] induced by the representation [math]\displaystyle{ (\theta,W_\theta) }[/math] of the subgroup [math]\displaystyle{ H. }[/math] Let [math]\displaystyle{ \chi_\rho }[/math] and [math]\displaystyle{ \chi_\theta }[/math] be the corresponding characters. Let [math]\displaystyle{ R }[/math] be a representative system of [math]\displaystyle{ G/H. }[/math] The induced character is given by

[math]\displaystyle{ \forall t \in G: \qquad \chi_\rho(t)=\sum_{r\in R,\atop r^{-1}tr \in H}^{} \chi_\theta (r^{-1}tr)=\frac{1}{|H|} \sum_{s\in G,\atop s^{-1}ts\in H}^{} \chi_\theta(s^{-1}ts). }[/math]

Frobenius reciprocity

As a preemptive summary, the lesson to take from Frobenius reciprocity is that the maps [math]\displaystyle{ \text{Res} }[/math] and [math]\displaystyle{ \text{Ind} }[/math] are adjoint to each other.

Let [math]\displaystyle{ W }[/math] be an irreducible representation of [math]\displaystyle{ H }[/math] and let [math]\displaystyle{ V }[/math] be an irreducible representation of [math]\displaystyle{ G, }[/math] then the Frobenius reciprocity tells us that [math]\displaystyle{ W }[/math] is contained in [math]\displaystyle{ \text{Res}(V) }[/math] as often as [math]\displaystyle{ \text{Ind}(W) }[/math] is contained in [math]\displaystyle{ V. }[/math]

Frobenius reciprocity. If [math]\displaystyle{ \psi\in\Complex _{\text{class}}(H) }[/math] and [math]\displaystyle{ \varphi\in\Complex _{\text{class}}(G) }[/math] we have [math]\displaystyle{ \langle \psi, \text{Res}(\varphi)\rangle_H=\langle \text{Ind}(\psi), \varphi\rangle_G. }[/math]

This statement is also valid for the inner product.

Mackey's irreducibility criterion

George Mackey established a criterion to verify the irreducibility of induced representations. For this we will first need some definitions and some specifications with respect to the notation.

Two representations [math]\displaystyle{ V_1 }[/math] and [math]\displaystyle{ V_2 }[/math] of a group [math]\displaystyle{ G }[/math] are called disjoint, if they have no irreducible component in common, i.e. if [math]\displaystyle{ \langle V_1,V_2\rangle_G =0. }[/math]

Let [math]\displaystyle{ G }[/math] be a group and let [math]\displaystyle{ H }[/math] be a subgroup. We define [math]\displaystyle{ H_s=sHs^{-1}\cap H }[/math] for [math]\displaystyle{ s \in G. }[/math] Let [math]\displaystyle{ (\rho, W) }[/math] be a representation of the subgroup [math]\displaystyle{ H. }[/math] This defines by restriction a representation [math]\displaystyle{ \text{Res}_{H_s}(\rho) }[/math] of [math]\displaystyle{ H_s. }[/math] We write [math]\displaystyle{ \text{Res}_s(\rho) }[/math] for [math]\displaystyle{ \text{Res}_{H_s}(\rho). }[/math] We also define another representation [math]\displaystyle{ \rho^s }[/math] of [math]\displaystyle{ H_s }[/math] by [math]\displaystyle{ \rho^s(t)=\rho(s^{-1}ts). }[/math] These two representations are not to be confused.

Mackey's irreducibility criterion. The induced representation [math]\displaystyle{ V=\text{Ind}^G_H(W) }[/math] is irreducible if and only if the following conditions are satisfied:

• [math]\displaystyle{ W }[/math] is irreducible
• For each [math]\displaystyle{ s\in G\setminus H }[/math] the two representations [math]\displaystyle{ \rho^s }[/math] and [math]\displaystyle{ \text{Res}_s(\rho) }[/math] of [math]\displaystyle{ H_s }[/math] are disjoint.

For the case of [math]\displaystyle{ H }[/math] normal, we have [math]\displaystyle{ H_s=H }[/math] and [math]\displaystyle{ \text{Res}_s(\rho)=\rho }[/math]. Thus we obtain the following:

Corollary. Let [math]\displaystyle{ H }[/math] be a normal subgroup of [math]\displaystyle{ G. }[/math] Then [math]\displaystyle{ \text{Ind}^G_H(\rho) }[/math] is irreducible if and only if [math]\displaystyle{ \rho }[/math] is irreducible and not isomorphic to the conjugates [math]\displaystyle{ \rho^s }[/math] for [math]\displaystyle{ s \notin H. }[/math]

Applications to special groups

In this section we present some applications of the so far presented theory to normal subgroups and to a special group, the semidirect product of a subgroup with an abelian normal subgroup.

Proposition. Let [math]\displaystyle{ A }[/math] be a normal subgroup of the group [math]\displaystyle{ G }[/math] and let [math]\displaystyle{ \rho: G\to\text{GL}(V) }[/math] be an irreducible representation of [math]\displaystyle{ G. }[/math] Then one of the following statements has to be valid:

• either there exists a proper subgroup [math]\displaystyle{ H }[/math] of [math]\displaystyle{ G }[/math] containing [math]\displaystyle{ A }[/math], and an irreducible representation [math]\displaystyle{ \eta }[/math] of [math]\displaystyle{ H }[/math] which induces [math]\displaystyle{ \rho }[/math],
• or [math]\displaystyle{ V }[/math] is an isotypic [math]\displaystyle{ \mathbb{C}A }[/math]-module.

Proof. Consider [math]\displaystyle{ V }[/math] as a [math]\displaystyle{ \mathbb{C}A }[/math]-module, and decompose it into isotypes as [math]\displaystyle{ V=\bigoplus_j{V_j} }[/math]. If this decomposition is trivial, we are in the second case. Otherwise, the larger [math]\displaystyle{ G }[/math]-action permutes these isotypic modules; because [math]\displaystyle{ V }[/math] is irreducible as a [math]\displaystyle{ \mathbb{C}G }[/math]-module, the permutation action is transitive (in fact primitive). Fix any [math]\displaystyle{ j }[/math]; the stabilizer in [math]\displaystyle{ G }[/math] of [math]\displaystyle{ V_j }[/math] is elementarily seen to exhibit the claimed properties.     [math]\displaystyle{ \Box }[/math]

Note that if [math]\displaystyle{ A }[/math] is abelian, then the isotypic modules of [math]\displaystyle{ A }[/math] are irreducible, of degree one, and all homotheties.

We obtain also the following

Corollary. Let [math]\displaystyle{ A }[/math] be an abelian normal subgroup of [math]\displaystyle{ G }[/math] and let [math]\displaystyle{ \tau }[/math] be any irreducible representation of [math]\displaystyle{ G. }[/math] We denote with [math]\displaystyle{ (G : A) }[/math] the index of [math]\displaystyle{ A }[/math] in [math]\displaystyle{ G. }[/math] Then [math]\displaystyle{ \deg(\tau)|(G : A). }[/math][1]

If [math]\displaystyle{ A }[/math] is an abelian subgroup of [math]\displaystyle{ G }[/math] (not necessarily normal), generally [math]\displaystyle{ \deg(\tau)|(G : A) }[/math] is not satisfied, but nevertheless [math]\displaystyle{ \deg(\tau) \leq (G : A) }[/math] is still valid.

Classification of representations of a semidirect product

In the following, let [math]\displaystyle{ G=A\rtimes H }[/math] be a semidirect product such that the normal semidirect factor, [math]\displaystyle{ A }[/math], is abelian. The irreducible representations of such a group [math]\displaystyle{ G, }[/math] can be classified by showing that all irreducible representations of [math]\displaystyle{ G }[/math] can be constructed from certain subgroups of [math]\displaystyle{ H }[/math]. This is the so-called method of “little groups” of Wigner and Mackey.

Since [math]\displaystyle{ A }[/math] is abelian, the irreducible characters of [math]\displaystyle{ A }[/math] have degree one and form the group [math]\displaystyle{ \Chi = \text{Hom}(A,\Complex^\times). }[/math] The group [math]\displaystyle{ G }[/math] acts on [math]\displaystyle{ \Chi }[/math] by [math]\displaystyle{ (s\chi)(a) = \chi(s^{-1}as) }[/math] for [math]\displaystyle{ s \in G, \chi \in \Chi, a \in A. }[/math]

Let [math]\displaystyle{ (\chi_j)_{j\in \Chi/H} }[/math] be a representative system of the orbit of [math]\displaystyle{ H }[/math] in [math]\displaystyle{ \Chi. }[/math] For every [math]\displaystyle{ j \in \Chi/H }[/math] let [math]\displaystyle{ H_j = \{t \in H : t\chi_j = \chi_j\}. }[/math] This is a subgroup of [math]\displaystyle{ H. }[/math] Let [math]\displaystyle{ G_j = A \cdot H_j }[/math] be the corresponding subgroup of [math]\displaystyle{ G. }[/math] We now extend the function [math]\displaystyle{ \chi_j }[/math] onto [math]\displaystyle{ G_j }[/math] by [math]\displaystyle{ \chi_j(at) = \chi_j(a) }[/math] for [math]\displaystyle{ a \in A, t \in H_j. }[/math] Thus, [math]\displaystyle{ \chi_j }[/math] is a class function on [math]\displaystyle{ G_j. }[/math] Moreover, since [math]\displaystyle{ t\chi_j = \chi_j }[/math] for all [math]\displaystyle{ t \in H_j, }[/math] it can be shown that [math]\displaystyle{ \chi_j }[/math] is a group homomorphism from [math]\displaystyle{ G_j }[/math] to [math]\displaystyle{ \Complex^\times. }[/math] Therefore, we have a representation of [math]\displaystyle{ G_j }[/math] of degree one which is equal to its own character.

Let now [math]\displaystyle{ \rho }[/math] be an irreducible representation of [math]\displaystyle{ H_j. }[/math] Then we obtain an irreducible representation [math]\displaystyle{ \tilde{\rho} }[/math] of [math]\displaystyle{ G_j, }[/math] by combining [math]\displaystyle{ \rho }[/math] with the canonical projection [math]\displaystyle{ G_j \to H_j. }[/math] Finally, we construct the tensor product of [math]\displaystyle{ \chi_j }[/math] and [math]\displaystyle{ \tilde{\rho}. }[/math] Thus, we obtain an irreducible representation [math]\displaystyle{ \chi_j\otimes \tilde{\rho} }[/math] of [math]\displaystyle{ G_j. }[/math]

To finally obtain the classification of the irreducible representations of [math]\displaystyle{ G }[/math] we use the representation [math]\displaystyle{ \theta_{j,\rho} }[/math] of [math]\displaystyle{ G, }[/math] which is induced by the tensor product [math]\displaystyle{ \chi_j\otimes \tilde{\rho}. }[/math] Thus, we achieve the following result:

Proposition.

• [math]\displaystyle{ \theta_{j,\rho} }[/math] is irreducible.
• If [math]\displaystyle{ \theta_{j,\rho} }[/math] and [math]\displaystyle{ \theta_{j',\rho'} }[/math] are isomorphic, then [math]\displaystyle{ j = j' }[/math] and additionally [math]\displaystyle{ \rho }[/math] is isomorphic to [math]\displaystyle{ \rho'. }[/math]
• Every irreducible representation of [math]\displaystyle{ G }[/math] is isomorphic to one of the [math]\displaystyle{ \theta_{j,\rho}. }[/math]

Amongst others, the criterion of Mackey and a conclusion based on the Frobenius reciprocity are needed for the proof of the proposition. Further details may be found in [1].

In other words, we classified all irreducible representations of [math]\displaystyle{ G=A \rtimes H. }[/math]

Representation ring

The representation ring of [math]\displaystyle{ G }[/math] is defined as the abelian group

[math]\displaystyle{ R(G)= \left \{ \left. \sum_{j=1}^m a_j \tau_j \right |\tau_1, \ldots, \tau_m \text{ all irreducible representations of } G \text{ up to isomorphism}, a_j\in\Z \right \}. }[/math]

With the multiplication provided by the tensor product, [math]\displaystyle{ R(G) }[/math] becomes a ring. The elements of [math]\displaystyle{ R(G) }[/math] are called virtual representations.

The character defines a ring homomorphism in the set of all class functions on [math]\displaystyle{ G }[/math] with complex values

[math]\displaystyle{ \begin{cases} \chi: R(G)\to\Complex _{\text{class}}(G)\\ \sum a_j \tau_j \mapsto \sum a_j \chi_j \end{cases} }[/math]

in which the [math]\displaystyle{ \chi_j }[/math] are the irreducible characters corresponding to the [math]\displaystyle{ \tau_j. }[/math]

Because a representation is determined by its character, [math]\displaystyle{ \chi }[/math] is injective. The images of [math]\displaystyle{ \chi }[/math] are called virtual characters.

As the irreducible characters form an orthonormal basis of [math]\displaystyle{ \Complex _{\text{class}}, \chi }[/math] induces an isomorphism

[math]\displaystyle{ \chi_\Complex : R(G)\otimes\Complex \to \Complex _{\text{class}}(G). }[/math]

This isomorphism is defined on a basis out of elementary tensors [math]\displaystyle{ (\tau_j\otimes1)_{j=1,\ldots, m} }[/math] by [math]\displaystyle{ \chi_{\Complex }(\tau_j\otimes1)=\chi_j }[/math] respectively [math]\displaystyle{ \chi_{\Complex }(\tau_j\otimes z)=z\chi_j, }[/math] and extended bilinearly.

We write [math]\displaystyle{ \mathcal{R}^+(G) }[/math] for the set of all characters of [math]\displaystyle{ G }[/math] and [math]\displaystyle{ \mathcal{R}(G) }[/math] to denote the group generated by [math]\displaystyle{ \mathcal{R}^+(G), }[/math] i.e. the set of all differences of two characters. It then holds that [math]\displaystyle{ \mathcal{R}(G)=\Z \chi_1\oplus \cdots \oplus\Z \chi_m }[/math] and [math]\displaystyle{ \mathcal{R}(G)=\text{Im}(\chi)=\chi(R(G)). }[/math] Thus, we have [math]\displaystyle{ R(G)\cong\mathcal{R}(G) }[/math] and the virtual characters correspond to the virtual representations in an optimal manner.

Since [math]\displaystyle{ \mathcal{R}(G)=\text{Im}(\chi) }[/math] holds, [math]\displaystyle{ \mathcal{R}(G) }[/math] is the set of all virtual characters. As the product of two characters provides another character, [math]\displaystyle{ \mathcal{R}(G) }[/math] is a subring of the ring [math]\displaystyle{ \Complex_{\text{class}}(G) }[/math] of all class functions on [math]\displaystyle{ G. }[/math] Because the [math]\displaystyle{ \chi_i }[/math] form a basis of [math]\displaystyle{ \Complex _{\text{class}}(G) }[/math] we obtain, just as in the case of [math]\displaystyle{ R(G), }[/math] an isomorphism [math]\displaystyle{ \Complex \otimes \mathcal{R}(G)\cong\Complex _{\text{class}}(G). }[/math]

Let [math]\displaystyle{ H }[/math] be a subgroup of [math]\displaystyle{ G. }[/math] The restriction thus defines a ring homomorphism [math]\displaystyle{ \mathcal{R}(G)\to \mathcal{R}(H), \phi\mapsto \phi|_H, }[/math] which will be denoted by [math]\displaystyle{ \text{Res}^G_H }[/math] or [math]\displaystyle{ \text{Res}. }[/math] Likewise, the induction on class functions defines a homomorphism of abelian groups [math]\displaystyle{ \mathcal{R}(H)\to \mathcal{R}(G), }[/math] which will be written as [math]\displaystyle{ \text{Ind}^G_H }[/math] or in short [math]\displaystyle{ \text{Ind}. }[/math]

According to the Frobenius reciprocity, these two homomorphisms are adjoint with respect to the bilinear forms [math]\displaystyle{ \langle \cdot,\cdot\rangle_H }[/math] and [math]\displaystyle{ \langle \cdot,\cdot\rangle_G. }[/math] Furthermore, the formula [math]\displaystyle{ \text{Ind}(\varphi\cdot \text{Res}(\psi))=\text{Ind}(\varphi)\cdot \psi }[/math] shows that the image of [math]\displaystyle{ \text{Ind}:\mathcal{R}(H)\to \mathcal{R}(G) }[/math] is an ideal of the ring [math]\displaystyle{ \mathcal{R}(G). }[/math]

By the restriction of representations, the map [math]\displaystyle{ \text{Res} }[/math] can be defined analogously for [math]\displaystyle{ R(G), }[/math] and by the induction we obtain the map [math]\displaystyle{ \text{Ind} }[/math] for [math]\displaystyle{ R(G). }[/math] Due to the Frobenius reciprocity, we get the result that these maps are adjoint to each other and that the image [math]\displaystyle{ \text{Im}(\text{Ind})=\text{Ind}(R(H)) }[/math] is an ideal of the ring [math]\displaystyle{ R(G). }[/math]

If [math]\displaystyle{ A }[/math] is a commutative ring, the homomorphisms [math]\displaystyle{ \text{Res} }[/math] and [math]\displaystyle{ \text{Ind} }[/math] may be extended to [math]\displaystyle{ A }[/math]–linear maps:

[math]\displaystyle{ \begin{cases} A\otimes \text{Res}: A\otimes R(G) \to A\otimes R(H)\\ \left (a \otimes \sum a_j \tau_j \right ) \mapsto \left (a \otimes \sum a_j \text{Res}(\tau_j) \right ) \end{cases}, \qquad \begin{cases} A\otimes \text{Ind}: A\otimes R(H) \to A\otimes R(G)\\ \left (a \otimes \sum a_j \eta_j \right )\mapsto \left (a \otimes \sum a_j \text{Ind}(\eta_j) \right ) \end{cases} }[/math]

in which [math]\displaystyle{ \eta_j }[/math] are all the irreducible representations of [math]\displaystyle{ H }[/math] up to isomorphism.

With [math]\displaystyle{ A=\Complex }[/math] we obtain in particular that [math]\displaystyle{ \text{Ind} }[/math] and [math]\displaystyle{ \text{Res} }[/math] supply homomorphisms between [math]\displaystyle{ \Complex _{\text{class}}(G) }[/math] and [math]\displaystyle{ \Complex _{\text{class}}(H). }[/math]

Let [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] be two groups with respective representations [math]\displaystyle{ (\rho_1, V_1) }[/math] and [math]\displaystyle{ (\rho_2, V_2). }[/math] Then, [math]\displaystyle{ \rho_1\otimes\rho_2 }[/math] is the representation of the direct product [math]\displaystyle{ G_1\times G_2 }[/math] as was shown in a previous section. Another result of that section was that all irreducible representations of [math]\displaystyle{ G_1\times G_2 }[/math] are exactly the representations [math]\displaystyle{ \eta_1\otimes\eta_2, }[/math] where [math]\displaystyle{ \eta_1 }[/math] and [math]\displaystyle{ \eta_2 }[/math] are irreducible representations of [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2, }[/math] respectively. This passes over to the representation ring as the identity [math]\displaystyle{ R(G_1\times G_2)=R(G_1)\otimes_{\Z} R(G_2), }[/math] in which [math]\displaystyle{ R(G_1)\otimes_{\Z} R(G_2) }[/math] is the tensor product of the representation rings as [math]\displaystyle{ \Z }[/math]–modules.

Induction theorems

Induction theorems relate the representation ring of a given finite group G to representation rings of a family X consisting of some subsets H of G. More precisely, for such a collection of subgroups, the induction functor yields a map

[math]\displaystyle{ \varphi: \text{Ind}:\bigoplus_{H\in X}\mathcal{R}(H) \to \mathcal{R}(G) }[/math]; induction theorems give criteria for the surjectivity of this map or closely related ones.

Artin's induction theorem is the most elementary theorem in this group of results. It asserts that the following are equivalent:

• The cokernel of [math]\displaystyle{ \varphi }[/math] is finite.
• [math]\displaystyle{ G }[/math] is the union of the conjugates of the subgroups belonging to [math]\displaystyle{ X, }[/math] i.e. [math]\displaystyle{ G=\bigcup_{H\in X \atop s\in G}sHs^{-1}. }[/math]

Since [math]\displaystyle{ \mathcal{R}(G) }[/math] is finitely generated as a group, the first point can be rephrased as follows:

• For each character [math]\displaystyle{ \chi }[/math] of [math]\displaystyle{ G, }[/math] there exist virtual characters [math]\displaystyle{ \chi_H \in \mathcal{R}(H), \,H\in X }[/math] and an integer [math]\displaystyle{ d\geq 1, }[/math] such that [math]\displaystyle{ d\cdot\chi = \sum_{H\in X}\text{Ind}^G_H(\chi_H). }[/math]

(Serre 1977) gives two proofs of this theorem. For example, since G is the union of its cyclic subgroups, every character of [math]\displaystyle{ G }[/math] is a linear combination with rational coefficients of characters induced by characters of cyclic subgroups of [math]\displaystyle{ G. }[/math] Since the representations of cyclic groups are well-understood, in particular the irreducible representations are one-dimensional, this gives a certain control over representations of G.

Under the above circumstances, it is not in general true that [math]\displaystyle{ \varphi }[/math] is surjective. Brauer's induction theorem asserts that [math]\displaystyle{ \varphi }[/math] is surjective, provided that X is the family of all elementary subgroups. Here a group H is elementary if there is some prime p such that H is the direct product of a cyclic group of order prime to [math]\displaystyle{ p }[/math] and a [math]\displaystyle{ p }[/math]–group. In other words, every character of [math]\displaystyle{ G }[/math] is a linear combination with integer coefficients of characters induced by characters of elementary subgroups. The elementary subgroups H arising in Brauer's theorem have a richer representation theory than cyclic groups, they at least have the property that any irreducible representation for such H is induced by a one-dimensional representation of a (necessarily also elementary) subgroup [math]\displaystyle{ K \subset H }[/math]. (This latter property can be shown to hold for any supersolvable group, which includes nilpotent groups and, in particular, elementary groups.) This ability to induce representations from degree 1 representations has some further consequences in the representation theory of finite groups.

Real representations

For proofs and more information about representations over general subfields of [math]\displaystyle{ \Complex }[/math] please refer to [2].

If a group [math]\displaystyle{ G }[/math] acts on a real vector space [math]\displaystyle{ V_0, }[/math] the corresponding representation on the complex vector space [math]\displaystyle{ V=V_0\otimes_\R \Complex }[/math] is called real ([math]\displaystyle{ V }[/math] is called the complexification of [math]\displaystyle{ V_0 }[/math]). The corresponding representation mentioned above is given by [math]\displaystyle{ s \cdot(v_0\otimes z) = (s\cdot v_0)\otimes z }[/math] for all [math]\displaystyle{ s\in G, v_0\in V_0, z\in \Complex. }[/math]

Let [math]\displaystyle{ \rho }[/math] be a real representation. The linear map [math]\displaystyle{ \rho(s) }[/math] is [math]\displaystyle{ \R }[/math]-valued for all [math]\displaystyle{ s\in G. }[/math] Thus, we can conclude that the character of a real representation is always real-valued. But not every representation with a real-valued character is real. To make this clear, let [math]\displaystyle{ G }[/math] be a finite, non-abelian subgroup of the group

[math]\displaystyle{ \text{SU}(2)= \left \{\begin{pmatrix} a & b \\ -\overline{b} & \overline{a} \end{pmatrix} \ : \ |a|^2+|b|^2=1 \right \}. }[/math]

Then [math]\displaystyle{ G \subset \text{SU}(2) }[/math] acts on [math]\displaystyle{ V=\Complex^2. }[/math] Since the trace of any matrix in [math]\displaystyle{ \text{SU}(2) }[/math] is real, the character of the representation is real-valued. Suppose [math]\displaystyle{ \rho }[/math] is a real representation, then [math]\displaystyle{ \rho(G) }[/math] would consist only of real-valued matrices. Thus, [math]\displaystyle{ G \subset \text{SU}(2)\cap\text{GL}_2(\R )=\text{SO}(2)=S^1. }[/math] However the circle group is abelian but [math]\displaystyle{ G }[/math] was chosen to be a non-abelian group. Now we only need to prove the existence of a non-abelian, finite subgroup of [math]\displaystyle{ \text{SU}(2). }[/math] To find such a group, observe that [math]\displaystyle{ \text{SU}(2) }[/math] can be identified with the units of the quaternions. Now let [math]\displaystyle{ G=\{\pm1,\pm i,\pm j, \pm ij \}. }[/math] The following two-dimensional representation of [math]\displaystyle{ G }[/math] is not real-valued, but has a real-valued character:

[math]\displaystyle{ \begin{cases} \rho : G \to \text{GL}_2(\Complex ) \\[4pt] \rho(\pm 1)=\begin{pmatrix} \pm1&0\\0& \pm1\end{pmatrix}, \quad \rho(\pm i)=\begin{pmatrix} \pm i&0\\0&\mp i\end{pmatrix}, \quad \rho(\pm j)=\begin{pmatrix} 0&\pm i\\ \pm i&0\end{pmatrix} \end{cases} }[/math]

Then the image of [math]\displaystyle{ \rho }[/math] is not real-valued, but nevertheless it is a subset of [math]\displaystyle{ \text{SU}(2). }[/math] Thus, the character of the representation is real.

Lemma. An irreducible representation [math]\displaystyle{ V }[/math] of [math]\displaystyle{ G }[/math] is real if and only if there exists a nondegenerate symmetric bilinear form [math]\displaystyle{ B }[/math] on [math]\displaystyle{ V }[/math] preserved by [math]\displaystyle{ G. }[/math]

An irreducible representation of [math]\displaystyle{ G }[/math] on a real vector space can become reducible when extending the field to [math]\displaystyle{ \Complex. }[/math] For example, the following real representation of the cyclic group is reducible when considered over [math]\displaystyle{ \Complex }[/math]

[math]\displaystyle{ \begin{cases} \rho : \Z /m\Z \to \text{GL}_2(\R ) \\[4pt] \rho(k)= \begin{pmatrix} \cos \left(\frac{2\pi ik}{m}\right ) & \sin \left (\frac{2\pi ik}{m} \right ) \\ -\sin \left(\frac{2\pi ik}{m} \right ) & \cos \left (\frac{2\pi ik}{m} \right )\end{pmatrix} \end{cases} }[/math]

Therefore, by classifying all the irreducible representations that are real over [math]\displaystyle{ \Complex, }[/math] we still haven't classified all the irreducible real representations. But we achieve the following:

Let [math]\displaystyle{ V_0 }[/math] be a real vector space. Let [math]\displaystyle{ G }[/math] act irreducibly on [math]\displaystyle{ V_0 }[/math] and let [math]\displaystyle{ V=V_0\otimes \Complex. }[/math] If [math]\displaystyle{ V }[/math] is not irreducible, there are exactly two irreducible factors which are complex conjugate representations of [math]\displaystyle{ G. }[/math]

Definition. A quaternionic representation is a (complex) representation [math]\displaystyle{ V, }[/math] which possesses a [math]\displaystyle{ G }[/math]–invariant anti-linear homomorphism [math]\displaystyle{ J:V\to V }[/math] satisfying [math]\displaystyle{ J^2=-\text{Id}. }[/math] Thus, a skew-symmetric, nondegenerate [math]\displaystyle{ G }[/math]–invariant bilinear form defines a quaternionic structure on [math]\displaystyle{ V. }[/math]

Theorem. An irreducible representation [math]\displaystyle{ V }[/math] is one and only one of the following:

(i) complex: [math]\displaystyle{ \chi_V }[/math] is not real-valued and there exists no [math]\displaystyle{ G }[/math]–invariant nondegenerate bilinear form on [math]\displaystyle{ V. }[/math]

(ii) real: [math]\displaystyle{ V=V_0\otimes \Complex , }[/math] a real representation; [math]\displaystyle{ V }[/math] has a [math]\displaystyle{ G }[/math]–invariant nondegenerate symmetric bilinear form.

(iii) quaternionic: [math]\displaystyle{ \chi_V }[/math] is real, but [math]\displaystyle{ V }[/math] is not real; [math]\displaystyle{ V }[/math] has a [math]\displaystyle{ G }[/math]–invariant skew-symmetric nondegenerate bilinear form.

Representations of particular groups

Symmetric groups

Representation of the symmetric groups [math]\displaystyle{ S_n }[/math] have been intensely studied. Conjugacy classes in [math]\displaystyle{ S_n }[/math] (and therefore, by the above, irreducible representations) correspond to partitions of n. For example, [math]\displaystyle{ S_3 }[/math] has three irreducible representations, corresponding to the partitions

3; 2+1; 1+1+1

of 3. For such a partition, a Young tableau is a graphical device depicting a partition. The irreducible representation corresponding to such a partition (or Young tableau) is called a Specht module.

Representations of different symmetric groups are related: any representation of [math]\displaystyle{ S_n \times S_m }[/math] yields a representation of [math]\displaystyle{ S_{n+m} }[/math] by induction, and vice versa by restriction. The direct sum of all these representation rings

[math]\displaystyle{ \bigoplus_{n \ge 0} R(S_n) }[/math]

inherits from these constructions the structure of a Hopf algebra which, it turns out, is closely related to symmetric functions.

Finite groups of Lie type

To a certain extent, the representations of the [math]\displaystyle{ GL_n(\mathbf F_q) }[/math] , as n varies, have a similar flavor as for the [math]\displaystyle{ S_n }[/math]; the above-mentioned induction process gets replaced by so-called parabolic induction. However, unlike for [math]\displaystyle{ S_n }[/math], where all representations can be obtained by induction of trivial representations, this is not true for [math]\displaystyle{ GL_n(\mathbf F_q) }[/math]. Instead, new building blocks, known as cuspidal representations, are needed.

Representations of [math]\displaystyle{ GL_n(\mathbf F_q) }[/math] and more generally, representations of finite groups of Lie type have been thoroughly studied. (Bonnafé 2010) describes the representations of [math]\displaystyle{ SL_2(\mathbf F_q) }[/math]. A geometric description of irreducible representations of such groups, including the above-mentioned cuspidal representations, is obtained by Deligne-Lusztig theory, which constructs such representation in the l-adic cohomology of Deligne-Lusztig varieties.

The similarity of the representation theory of [math]\displaystyle{ S_n }[/math] and [math]\displaystyle{ GL_n(\mathbf F_q) }[/math] goes beyond finite groups. The philosophy of cusp forms highlights the kinship of representation theoretic aspects of these types of groups with general linear groups of local fields such as Q_p and of the ring of adeles, see (Bump 2004).

Outlook—Representations of compact groups

The theory of representations of compact groups may be, to some degree, extended to locally compact groups. The representation theory unfolds in this context great importance for harmonic analysis and the study of automorphic forms. For proofs, further information and for a more detailed insight which is beyond the scope of this chapter please consult [4] and [5].

Definition and properties

A topological group is a group together with a topology with respect to which the group composition and the inversion are continuous. Such a group is called compact, if any cover of [math]\displaystyle{ G, }[/math] which is open in the topology, has a finite subcover. Closed subgroups of a compact group are compact again.

Let [math]\displaystyle{ G }[/math] be a compact group and let [math]\displaystyle{ V }[/math] be a finite-dimensional [math]\displaystyle{ \Complex }[/math]–vector space. A linear representation of [math]\displaystyle{ G }[/math] to [math]\displaystyle{ V }[/math] is a continuous group homomorphism [math]\displaystyle{ \rho: G \to \text{GL}(V), }[/math] i.e. [math]\displaystyle{ \rho(s)v }[/math] is a continuous function in the two variables [math]\displaystyle{ s\in G }[/math] and [math]\displaystyle{ v\in V. }[/math]

A linear representation of [math]\displaystyle{ G }[/math] into a Banach space [math]\displaystyle{ V }[/math] is defined to be a continuous group homomorphism of [math]\displaystyle{ G }[/math] into the set of all bijective bounded linear operators on [math]\displaystyle{ V }[/math] with a continuous inverse. Since [math]\displaystyle{ \pi(g)^{-1}=\pi(g^{-1}), }[/math] we can do without the last requirement. In the following, we will consider in particular representations of compact groups in Hilbert spaces.

Just as with finite groups, we can define the group algebra and the convolution algebra. However, the group algebra provides no helpful information in the case of infinite groups, because the continuity condition gets lost during the construction. Instead the convolution algebra [math]\displaystyle{ L^1(G) }[/math] takes its place.

Most properties of representations of finite groups can be transferred with appropriate changes to compact groups. For this we need a counterpart to the summation over a finite group:

Existence and uniqueness of the Haar measure

On a compact group [math]\displaystyle{ G }[/math] there exists exactly one measure [math]\displaystyle{ dt, }[/math] such that:

• It is a left-translation-invariant measure

[math]\displaystyle{ \forall s \in G: \quad \int_{G} f(t) dt = \int_{G} f(st)dt. }[/math]

• The whole group has unit measure:

[math]\displaystyle{ \int_{G} dt=1, }[/math]

Such a left-translation-invariant, normed measure is called Haar measure of the group [math]\displaystyle{ G. }[/math]

Since [math]\displaystyle{ G }[/math] is compact, it is possible to show that this measure is also right-translation-invariant, i.e. it also applies

[math]\displaystyle{ \forall s \in G: \quad \int_{G} f(t) dt = \int_{G} f(ts)dt. }[/math]

By the scaling above the Haar measure on a finite group is given by [math]\displaystyle{ dt(s)=\tfrac{1}{|G|} }[/math] for all [math]\displaystyle{ s\in G. }[/math]

All the definitions to representations of finite groups that are mentioned in the section ”Properties”, also apply to representations of compact groups. But there are some modifications needed:

To define a subrepresentation we now need a closed subspace. This was not necessary for finite-dimensional representation spaces, because in this case every subspace is already closed. Furthermore, two representations [math]\displaystyle{ \rho, \pi }[/math] of a compact group [math]\displaystyle{ G }[/math] are called equivalent, if there exists a bijective, continuous, linear operator [math]\displaystyle{ T }[/math] between the representation spaces whose inverse is also continuous and which satisfies [math]\displaystyle{ T\circ\rho(s)=\pi(s)\circ T }[/math] for all [math]\displaystyle{ s\in G. }[/math]

If [math]\displaystyle{ T }[/math] is unitary, the two representations are called unitary equivalent.

To obtain a [math]\displaystyle{ G }[/math]–invariant inner product from a not [math]\displaystyle{ G }[/math]–invariant, we now have to use the integral over [math]\displaystyle{ G }[/math] instead of the sum. If [math]\displaystyle{ (\cdot|\cdot) }[/math] is an inner product on a Hilbert space [math]\displaystyle{ V, }[/math] which is not invariant with respect to the representation [math]\displaystyle{ \rho }[/math] of [math]\displaystyle{ G, }[/math] then

[math]\displaystyle{ (v|u)_\rho=\int_G(\rho(t)v|\rho(t)u)dt }[/math]

is a [math]\displaystyle{ G }[/math]–invariant inner product on [math]\displaystyle{ V }[/math] due to the properties of the Haar measure [math]\displaystyle{ dt. }[/math] Thus, we can assume every representation on a Hilbert space to be unitary.

Let [math]\displaystyle{ G }[/math] be a compact group and let [math]\displaystyle{ s\in G. }[/math] Let [math]\displaystyle{ L^2(G) }[/math] be the Hilbert space of the square integrable functions on [math]\displaystyle{ G. }[/math] We define the operator [math]\displaystyle{ L_s }[/math] on this space by [math]\displaystyle{ L_s\Phi(t)=\Phi(s^{-1}t), }[/math] where [math]\displaystyle{ \Phi\in L^2(G), t\in G. }[/math]

The map [math]\displaystyle{ s\mapsto L_s }[/math] is a unitary representation of [math]\displaystyle{ G. }[/math] It is called left-regular representation. The right-regular representation is defined similarly. As the Haar measure of [math]\displaystyle{ G }[/math] is also right-translation-invariant, the operator [math]\displaystyle{ R_s }[/math] on [math]\displaystyle{ L^2(G) }[/math] is given by [math]\displaystyle{ R_s\Phi(t)=\Phi(ts). }[/math] The right-regular representation is then the unitary representation given by [math]\displaystyle{ s\mapsto R_s. }[/math] The two representations [math]\displaystyle{ s\mapsto L_s }[/math] and [math]\displaystyle{ s\mapsto R_s }[/math] are dual to each other.

If [math]\displaystyle{ G }[/math] is infinite, these representations have no finite degree. The left- and right-regular representation as defined at the beginning are isomorphic to the left- and right-regular representation as defined above, if the group [math]\displaystyle{ G }[/math] is finite. This is due to the fact that in this case [math]\displaystyle{ L^2(G)\cong L^1(G)\cong\Complex [G]. }[/math]

Constructions and decompositions

The different ways of constructing new representations from given ones can be used for compact groups as well, except for the dual representation with which we will deal later. The direct sum and the tensor product with a finite number of summands/factors are defined in exactly the same way as for finite groups. This is also the case for the symmetric and alternating square. However, we need a Haar measure on the direct product of compact groups in order to extend the theorem saying that the irreducible representations of the product of two groups are (up to isomorphism) exactly the tensor product of the irreducible representations of the factor groups. First, we note that the direct product [math]\displaystyle{ G_1\times G_2 }[/math] of two compact groups is again a compact group when provided with the product topology. The Haar measure on the direct product is then given by the product of the Haar measures on the factor groups.

For the dual representation on compact groups we require the topological dual [math]\displaystyle{ V' }[/math] of the vector space [math]\displaystyle{ V. }[/math] This is the vector space of all continuous linear functionals from the vector space [math]\displaystyle{ V }[/math] into the base field. Let [math]\displaystyle{ \pi }[/math] be a representation of a compact group [math]\displaystyle{ G }[/math] in [math]\displaystyle{ V. }[/math]

The dual representation [math]\displaystyle{ \pi':G\to\text{GL}(V') }[/math] is defined by the property

[math]\displaystyle{ \forall v\in V, \forall v'\in V', \forall s\in G: \qquad \left \langle\pi'(s)v',\pi(s)v \right \rangle=\langle v',v\rangle := v'(v). }[/math]

Thus, we can conclude that the dual representation is given by [math]\displaystyle{ \pi'(s)v'=v'\circ\pi(s^{-1}) }[/math] for all [math]\displaystyle{ v'\in V', s\in G. }[/math] The map [math]\displaystyle{ \pi' }[/math] is again a continuous group homomorphism and thus a representation.

On Hilbert spaces: [math]\displaystyle{ \pi }[/math] is irreducible if and only if [math]\displaystyle{ \pi' }[/math] is irreducible.

By transferring the results of the section decompositions to compact groups, we obtain the following theorems:

Theorem. Every irreducible representation [math]\displaystyle{ (\tau,V_\tau) }[/math] of a compact group into a Hilbert space is finite-dimensional and there exists an inner product on [math]\displaystyle{ V_\tau }[/math] such that [math]\displaystyle{ \tau }[/math] is unitary. Since the Haar measure is normalized, this inner product is unique.

Every representation of a compact group is isomorphic to a direct Hilbert sum of irreducible representations.

Let [math]\displaystyle{ (\rho,V_\rho) }[/math] be a unitary representation of the compact group [math]\displaystyle{ G. }[/math] Just as for finite groups we define for an irreducible representation [math]\displaystyle{ (\tau, V_\tau) }[/math] the isotype or isotypic component in [math]\displaystyle{ \rho }[/math] to be the subspace

[math]\displaystyle{ V_\rho(\tau)=\sum_{V_{\tau} \cong U\subset V_\rho} U. }[/math]

This is the sum of all invariant closed subspaces [math]\displaystyle{ U, }[/math] which are [math]\displaystyle{ G }[/math]–isomorphic to [math]\displaystyle{ V_\tau. }[/math]

Note that the isotypes of not equivalent irreducible representations are pairwise orthogonal.

Theorem.

(i) [math]\displaystyle{ V_\rho(\tau) }[/math] is a closed invariant subspace of [math]\displaystyle{ V_\rho. }[/math]

(ii) [math]\displaystyle{ V_\rho(\tau) }[/math] is [math]\displaystyle{ G }[/math]–isomorphic to the direct sum of copies of [math]\displaystyle{ V_\tau. }[/math]

(iii) Canonical decomposition: [math]\displaystyle{ V_\rho }[/math] is the direct Hilbert sum of the isotypes [math]\displaystyle{ V_\rho(\tau), }[/math] in which [math]\displaystyle{ \tau }[/math] passes through all the isomorphism classes of the irreducible representations.

The corresponding projection to the canonical decomposition [math]\displaystyle{ p_\tau: V\to V(\tau), }[/math] in which [math]\displaystyle{ V(\tau) }[/math] is an isotype of [math]\displaystyle{ V, }[/math] is for compact groups given by

[math]\displaystyle{ p_\tau(v)=n_\tau\int_G\overline{\chi_\tau(t)}\rho(t)(v)dt, }[/math]

where [math]\displaystyle{ n_\tau=\dim (V(\tau)) }[/math] and [math]\displaystyle{ \chi_\tau }[/math] is the character corresponding to the irreducible representation [math]\displaystyle{ \tau. }[/math]

Projection formula

For every representation [math]\displaystyle{ (\rho,V) }[/math] of a compact group [math]\displaystyle{ G }[/math] we define

[math]\displaystyle{ V^G=\{v\in V : \rho(s)v=v \,\,\,\forall s \in G\}. }[/math]

In general [math]\displaystyle{ \rho(s): V\to V }[/math] is not [math]\displaystyle{ G }[/math]–linear. Let

[math]\displaystyle{ Pv:= \int_G \rho(s)vds. }[/math]

The map [math]\displaystyle{ P }[/math] is defined as endomorphism on [math]\displaystyle{ V }[/math] by having the property

[math]\displaystyle{ \left. \left (\int_G \rho(s)v ds \right |w \right )=\int_G (\rho(s)v|w) ds, }[/math]

which is valid for the inner product of the Hilbert space [math]\displaystyle{ V. }[/math]

Then [math]\displaystyle{ P }[/math] is [math]\displaystyle{ G }[/math]–linear, because of

[math]\displaystyle{ \begin{align} \left. \left (\int_G \rho(s)(\rho(t)v) ds \right |w \right )&=\int_G \left. \left (\rho \left (tst^{-1} \right )(\rho(t)v) \right |w \right ) ds \\ &= \int_G (\rho(ts)v|w) ds \\ &= \int(\rho(t)\rho(s)v|w) ds \\ &= \left. \left (\rho(t)\int_G \rho(s)v ds \right |w \right ), \end{align} }[/math]

where we used the invariance of the Haar measure.

Proposition. The map [math]\displaystyle{ P }[/math] is a projection from [math]\displaystyle{ V }[/math] to [math]\displaystyle{ V^G. }[/math]

If the representation is finite-dimensional, it is possible to determine the direct sum of the trivial subrepresentation just as in the case of finite groups.

Characters, Schur's lemma and the inner product

Generally, representations of compact groups are investigated on Hilbert- and Banach spaces. In most cases they are not finite-dimensional. Therefore, it is not useful to refer to characters when speaking about representations of compact groups. Nevertheless, in most cases it is possible to restrict the study to the case of finite dimensions:

Since irreducible representations of compact groups are finite-dimensional and unitary (see results from the first subsection), we can define irreducible characters in the same way as it was done for finite groups.

As long as the constructed representations stay finite-dimensional, the characters of the newly constructed representations may be obtained in the same way as for finite groups.

Schur's lemma is also valid for compact groups:

Let [math]\displaystyle{ (\pi,V) }[/math] be an irreducible unitary representation of a compact group [math]\displaystyle{ G. }[/math] Then every bounded operator [math]\displaystyle{ T:V\to V }[/math] satisfying the property [math]\displaystyle{ T\circ\pi(s)=\pi(s)\circ T }[/math] for all [math]\displaystyle{ s\in G, }[/math] is a scalar multiple of the identity, i.e. there exists [math]\displaystyle{ \lambda \in \Complex }[/math] such that [math]\displaystyle{ T=\lambda \text{Id}. }[/math]

Definition. The formula

[math]\displaystyle{ (\Phi|\Psi)=\int_G\Phi(t)\overline{\Psi(t)}dt. }[/math]

defines an inner product on the set of all square integrable functions [math]\displaystyle{ L^2(G) }[/math] of a compact group [math]\displaystyle{ G. }[/math] Likewise

[math]\displaystyle{ \langle\Phi,\Psi\rangle=\int_G\Phi(t)\Psi(t^{-1})dt. }[/math]

defines a bilinear form on [math]\displaystyle{ L^2(G) }[/math] of a compact group [math]\displaystyle{ G. }[/math]

The bilinear form on the representation spaces is defined exactly as it was for finite groups and analogous to finite groups the following results are therefore valid:

Theorem. Let [math]\displaystyle{ \chi }[/math] and [math]\displaystyle{ \chi' }[/math] be the characters of two non-isomorphic irreducible representations [math]\displaystyle{ V }[/math] and [math]\displaystyle{ V', }[/math] respectively. Then the following is valid

• [math]\displaystyle{ (\chi|\chi')=0. }[/math]
• [math]\displaystyle{ (\chi|\chi)=1, }[/math] i.e. [math]\displaystyle{ \chi }[/math] has "norm" [math]\displaystyle{ 1. }[/math]

Theorem. Let [math]\displaystyle{ V }[/math] be a representation of [math]\displaystyle{ G }[/math] with character [math]\displaystyle{ \chi_V. }[/math] Suppose [math]\displaystyle{ W }[/math] is an irreducible representation of [math]\displaystyle{ G }[/math] with character [math]\displaystyle{ \chi_W. }[/math] The number of subrepresentations of [math]\displaystyle{ V }[/math] equivalent to [math]\displaystyle{ W }[/math] is independent of any given decomposition for [math]\displaystyle{ V }[/math] and is equal to the inner product [math]\displaystyle{ (\chi_V|\chi_W). }[/math]

Irreducibility Criterion. Let [math]\displaystyle{ \chi }[/math] be the character of the representation [math]\displaystyle{ V, }[/math] then [math]\displaystyle{ (\chi|\chi) }[/math] is a positive integer. Moreover [math]\displaystyle{ (\chi|\chi)=1 }[/math] if and only if [math]\displaystyle{ V }[/math] is irreducible.

Therefore, using the first theorem, the characters of irreducible representations of [math]\displaystyle{ G }[/math] form an orthonormal set on [math]\displaystyle{ L^2(G) }[/math] with respect to this inner product.

Corollary. Every irreducible representation [math]\displaystyle{ V }[/math] of [math]\displaystyle{ G }[/math] is contained [math]\displaystyle{ \dim (V) }[/math]–times in the left-regular representation.

Lemma. Let [math]\displaystyle{ G }[/math] be a compact group. Then the following statements are equivalent:

• [math]\displaystyle{ G }[/math] is abelian.
• All the irreducible representations of [math]\displaystyle{ G }[/math] have degree [math]\displaystyle{ 1. }[/math]

Orthonormal Property. Let [math]\displaystyle{ G }[/math] be a group. The non-isomorphic irreducible representations of [math]\displaystyle{ G }[/math] form an orthonormal basis in [math]\displaystyle{ L^2(G) }[/math] with respect to this inner product.

As we already know that the non-isomorphic irreducible representations are orthonormal, we only need to verify that they generate [math]\displaystyle{ L^2(G). }[/math] This may be done, by proving that there exists no non-zero square integrable function on [math]\displaystyle{ G }[/math] orthogonal to all the irreducible characters.

Just as in the case of finite groups, the number of the irreducible representations up to isomorphism of a group [math]\displaystyle{ G }[/math] equals the number of conjugacy classes of [math]\displaystyle{ G. }[/math] However, because a compact group has in general infinitely many conjugacy classes, this does not provide any useful information.

The induced representation

If [math]\displaystyle{ H }[/math] is a closed subgroup of finite index in a compact group [math]\displaystyle{ G, }[/math] the definition of the induced representation for finite groups may be adopted.

However, the induced representation can be defined more generally, so that the definition is valid independent of the index of the subgroup [math]\displaystyle{ H. }[/math]

For this purpose let [math]\displaystyle{ (\eta, V_\eta) }[/math] be a unitary representation of the closed subgroup [math]\displaystyle{ H. }[/math] The continuous induced representation [math]\displaystyle{ \text{Ind}^G_H(\eta)=(I,V_I) }[/math] is defined as follows:

Let [math]\displaystyle{ V_I }[/math] denote the Hilbert space of all measurable, square integrable functions [math]\displaystyle{ \Phi:G\to V_\eta }[/math] with the property [math]\displaystyle{ \Phi(ls)=\eta(l)\Phi(s) }[/math] for all [math]\displaystyle{ l\in H, s\in G. }[/math] The norm is given by

[math]\displaystyle{ \|\Phi\|_G=\text{sup}_{s\in G}\|\Phi(s)\| }[/math]

and the representation [math]\displaystyle{ I }[/math] is given as the right-translation: [math]\displaystyle{ I(s)\Phi(k)=\Phi(ks). }[/math]

The induced representation is then again a unitary representation.

Since [math]\displaystyle{ G }[/math] is compact, the induced representation can be decomposed into the direct sum of irreducible representations of [math]\displaystyle{ G. }[/math] Note that all irreducible representations belonging to the same isotype appear with a multiplicity equal to [math]\displaystyle{ \dim (\text{Hom}_G(V_\eta,V_I))=\langle V_\eta,V_I \rangle_G. }[/math]

Let [math]\displaystyle{ (\rho, V_\rho) }[/math] be a representation of [math]\displaystyle{ G, }[/math] then there exists a canonical isomorphism

[math]\displaystyle{ T: \text{Hom}_G(V_\rho, I^G_H(\eta))\to \text{Hom}_H(V_\rho|_H, V_\eta). }[/math]

The Frobenius reciprocity transfers, together with the modified definitions of the inner product and of the bilinear form, to compact groups. The theorem now holds for square integrable functions on [math]\displaystyle{ G }[/math] instead of class functions, but the subgroup [math]\displaystyle{ H }[/math] must be closed.

The Peter-Weyl Theorem

Another important result in the representation theory of compact groups is the Peter-Weyl Theorem. It is usually presented and proven in harmonic analysis, as it represents one of its central and fundamental statements.

The Peter-Weyl Theorem. Let [math]\displaystyle{ G }[/math] be a compact group. For every irreducible representation [math]\displaystyle{ (\tau, V_\tau) }[/math] of [math]\displaystyle{ G }[/math] let [math]\displaystyle{ \{e_1,\ldots,e_{\dim (\tau)}\} }[/math] be an orthonormal basis of [math]\displaystyle{ V_\tau. }[/math] We define the matrix coefficients [math]\displaystyle{ \tau_{k,l}(s)=\langle\tau(s)e_k,e_l\rangle }[/math] for [math]\displaystyle{ k,l \in \{1, \ldots, \dim (\tau)\}, s\in G. }[/math] Then we have the following orthonormal basis of [math]\displaystyle{ L^2(G) }[/math]:

[math]\displaystyle{ \left (\sqrt{\dim (\tau)}\tau_{k,l} \right)_{k,l} }[/math]

We can reformulate this theorem to obtain a generalization of the Fourier series for functions on compact groups:

The Peter-Weyl Theorem (Second version). There exists a natural [math]\displaystyle{ G\times G }[/math]–isomorphism

[math]\displaystyle{ L^2(G)\cong_{G\times G} \widehat{\bigoplus}_{\tau \in \widehat{G}}\text{End}(V_\tau)\cong_{G\times G} \widehat{\bigoplus}_{\tau \in \widehat{G}} \tau\otimes\tau^* }[/math]

in which [math]\displaystyle{ \widehat{G} }[/math] is the set of all irreducible representations of [math]\displaystyle{ G }[/math] up to isomorphism and [math]\displaystyle{ V_\tau }[/math] is the representation space corresponding to [math]\displaystyle{ \tau. }[/math] More concretely:

[math]\displaystyle{ \begin{cases}\Phi \mapsto \sum_{\tau\in \widehat{G}}\tau(\Phi) \\[5pt] \tau(\Phi)=\int_G \Phi(t)\tau(t)dt\in \text{End}(V_\tau) \end{cases} }[/math]

History

The general features of the representation theory of a finite group G, over the complex numbers, were discovered by Ferdinand Georg Frobenius in the years before 1900. Later the modular representation theory of Richard Brauer was developed.

See also

• Character theory
• Real representation
• Schur orthogonality relations
• McKay conjecture
• Burnside ring

Literature

• Bonnafé, Cedric (2010). Representations of SL2(Fq). Algebra and Applications. 13. Springer. ISBN 9780857291578. https://books.google.com/books?id=xehwfWBV5EwC. 
• Bump, Daniel (2004), Lie Groups, Graduate Texts in Mathematics, 225, New York: Springer-Verlag, ISBN 0-387-21154-3 
• [1] Serre, Jean-Pierre (1977), Linear Representations of Finite Groups, New York: Springer Verlag, ISBN 0-387-90190-6, https://archive.org/details/linearrepresenta1977serr 
• [2] Fulton, William; Harris, Joe: Representation Theory A First Course. Springer-Verlag, New York 1991, ISBN 0-387-97527-6.
• [3] Alperin, J.L.; Bell, Rowen B.: Groups and Representations Springer-Verlag, New York 1995, ISBN 0-387-94525-3.
• [4] Deitmar, Anton: Automorphe Formen Springer-Verlag 2010, ISBN 978-3-642-12389-4, p. 89-93,185-189
• [5] Echterhoff, Siegfried; Deitmar, Anton: Principles of harmonic analysis Springer-Verlag 2009, ISBN 978-0-387-85468-7, p. 127-150
• [6] Lang, Serge: Algebra Springer-Verlag, New York 2002, ISBN 0-387-95385-X, p. 663-729
• [7] Sengupta, Ambar (2012). Representing finite groups: a semisimple introduction. New York. ISBN 9781461412311. OCLC 769756134.