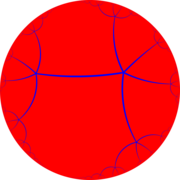
Order-5 hexagonal tiling honeycomb

Order-5 hexagonal tiling honeycomb
Perspective projection view from center of Poincaré disk model
Type	Hyperbolic regular honeycomb Paracompact uniform honeycomb
Schläfli symbol	{6,3,5}
Coxeter-Dynkin diagrams	↔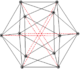
Cells	{6,3}
Faces	hexagon {6}
Edge figure	pentagon {5}
Vertex figure	icosahedron
Dual	Order-6 dodecahedral honeycomb
Coxeter group	[math]\displaystyle{ \overline{HV}_3 }[/math], [5,3,6]
Properties	Regular

In the field of hyperbolic geometry, the order-5 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell consists of a hexagonal tiling whose vertices lie on a horosphere, a flat plane in hyperbolic space that approaches a single ideal point at infinity.

The Schläfli symbol of the order-5 hexagonal tiling honeycomb is {6,3,5}. Since that of the hexagonal tiling is {6,3}, this honeycomb has five such hexagonal tilings meeting at each edge. Since the Schläfli symbol of the icosahedron is {3,5}, the vertex figure of this honeycomb is an icosahedron. Thus, 20 hexagonal tilings meet at each vertex of this honeycomb.

A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.

Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.

Symmetry

A lower-symmetry construction of index 120, [6,(3,5)^*], exists with regular dodecahedral fundamental domains, and an icosahedral Coxeter-Dynkin diagram with 6 axial infinite-order (ultraparallel) branches.

Images

The order-5 hexagonal tiling honeycomb is similar to the 2D hyperbolic regular paracompact order-5 apeirogonal tiling, {∞,5}, with five apeirogonal faces meeting around every vertex.

Related polytopes and honeycombs

The order-5 hexagonal tiling honeycomb is a regular hyperbolic honeycomb in 3-space, and one of 11 which are paracompact.

There are 15 uniform honeycombs in the [6,3,5] Coxeter group family, including this regular form, and its regular dual, the order-6 dodecahedral honeycomb.

The order-5 hexagonal tiling honeycomb has a related alternation honeycomb, represented by ↔ , with icosahedron and triangular tiling cells.

It is a part of sequence of regular hyperbolic honeycombs of the form {6,3,p}, with hexagonal tiling facets:

It is also part of a sequence of regular polychora and honeycombs with icosahedral vertex figures:

Rectified order-5 hexagonal tiling honeycomb

Rectified order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	r{6,3,5} or t1{6,3,5}
Coxeter diagrams	↔
Cells	{3,5} r{6,3} or h2{6,3} 40px
Faces	triangle {3} hexagon {6}
Vertex figure	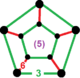pentagonal prism
Coxeter groups	[math]\displaystyle{ {\overline{HV}_3} }[/math], [5,3,6] [math]\displaystyle{ {\overline{HP}_3} }[/math], [5,3[3]]
Properties	Vertex-transitive, edge-transitive

The rectified order-5 hexagonal tiling honeycomb, t₁{6,3,5}, has icosahedron and trihexagonal tiling facets, with a pentagonal prism vertex figure.

It is similar to the 2D hyperbolic infinite-order square tiling, r{∞,5} with pentagon and apeirogonal faces. All vertices are on the ideal surface.

Truncated order-5 hexagonal tiling honeycomb

Truncated order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t{6,3,5} or t0,1{6,3,5}
Coxeter diagram
Cells	{3,5} t{6,3}
Faces	triangle {3} dodecagon {12}
Vertex figure	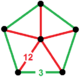pentagonal pyramid
Coxeter groups	[math]\displaystyle{ {\overline{HV}}_3 }[/math], [5,3,6]
Properties	Vertex-transitive

The truncated order-5 hexagonal tiling honeycomb, t_0,1{6,3,5}, has icosahedron and truncated hexagonal tiling facets, with a pentagonal pyramid vertex figure.

Bitruncated order-5 hexagonal tiling honeycomb

Bitruncated order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	2t{6,3,5} or t1,2{6,3,5}
Coxeter diagram	↔
Cells	t{3,6} t{3,5}
Faces	pentagon {5} hexagon {6}
Vertex figure	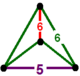digonal disphenoid
Coxeter groups	[math]\displaystyle{ {\overline{HV}}_3 }[/math], [5,3,6] [math]\displaystyle{ {\overline{HP}}_3 }[/math], [5,3[3]]
Properties	Vertex-transitive

The bitruncated order-5 hexagonal tiling honeycomb, t_1,2{6,3,5}, has hexagonal tiling and truncated icosahedron facets, with a digonal disphenoid vertex figure.

Cantellated order-5 hexagonal tiling honeycomb

Cantellated order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	rr{6,3,5} or t0,2{6,3,5}
Coxeter diagram
Cells	r{3,5} rr{6,3} 40px {}x{5}
Faces	triangle {3} square {4} pentagon {5} hexagon {6}
Vertex figure	wedge
Coxeter groups	[math]\displaystyle{ {\overline{HV}}_3 }[/math], [5,3,6]
Properties	Vertex-transitive

The cantellated order-5 hexagonal tiling honeycomb, t_0,2{6,3,5}, has icosidodecahedron, rhombitrihexagonal tiling, and pentagonal prism facets, with a wedge vertex figure.

Cantitruncated order-5 hexagonal tiling honeycomb

Cantitruncated order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	tr{6,3,5} or t0,1,2{6,3,5}
Coxeter diagram
Cells	t{3,5} tr{6,3} 40px {}x{5}
Faces	square {4} pentagon {5} hexagon {6} dodecagon {12}
Vertex figure	mirrored sphenoid
Coxeter groups	[math]\displaystyle{ {\overline{HV}}_3 }[/math], [5,3,6]
Properties	Vertex-transitive

The cantitruncated order-5 hexagonal tiling honeycomb, t_0,1,2{6,3,5}, has truncated icosahedron, truncated trihexagonal tiling, and pentagonal prism facets, with a mirrored sphenoid vertex figure.

Runcinated order-5 hexagonal tiling honeycomb

Runcinated order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t0,3{6,3,5}
Coxeter diagram
Cells	{6,3} {5,3} 40px {}x{6} 40px {}x{5}
Faces	square {4} pentagon {5} hexagon {6}
Vertex figure	irregular triangular antiprism
Coxeter groups	[math]\displaystyle{ {\overline{HV}}_3 }[/math], [5,3,6]
Properties	Vertex-transitive

The runcinated order-5 hexagonal tiling honeycomb, t_0,3{6,3,5}, has dodecahedron, hexagonal tiling, pentagonal prism, and hexagonal prism facets, with an irregular triangular antiprism vertex figure.

Runcitruncated order-5 hexagonal tiling honeycomb

Runcitruncated order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t0,1,3{6,3,5}
Coxeter diagram
Cells	t{6,3} rr{5,3} 40px {}x{5} 40px {}x{12}
Faces	triangle {3} square {4} pentagon {5} dodecagon {12}
Vertex figure	isosceles-trapezoidal pyramid
Coxeter groups	[math]\displaystyle{ {\overline{HV}}_3 }[/math], [5,3,6]
Properties	Vertex-transitive

The runcitruncated order-5 hexagonal tiling honeycomb, t_0,1,3{6,3,5}, has truncated hexagonal tiling, rhombicosidodecahedron, pentagonal prism, and dodecagonal prism cells, with an isosceles-trapezoidal pyramid vertex figure.

Runcicantellated order-5 hexagonal tiling honeycomb

The runcicantellated order-5 hexagonal tiling honeycomb is the same as the runcitruncated order-6 dodecahedral honeycomb.

Omnitruncated order-5 hexagonal tiling honeycomb

Omnitruncated order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t0,1,2,3{6,3,5}
Coxeter diagram
Cells	tr{6,3} tr{5,3} 40px {}x{10} 40px {}x{12}
Faces	square {4} hexagon {6} decagon {10} dodecagon {12}
Vertex figure	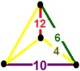irregular tetrahedron
Coxeter groups	[math]\displaystyle{ {\overline{HV}}_3 }[/math], [5,3,6]
Properties	Vertex-transitive

The omnitruncated order-5 hexagonal tiling honeycomb, t_0,1,2,3{6,3,5}, has truncated trihexagonal tiling, truncated icosidodecahedron, decagonal prism, and dodecagonal prism facets, with an irregular tetrahedral vertex figure.

Alternated order-5 hexagonal tiling honeycomb

Alternated order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb Semiregular honeycomb
Schläfli symbol	h{6,3,5}
Coxeter diagram	↔
Cells	{3[3]} {3,5}
Faces	triangle {3}
Vertex figure	truncated icosahedron
Coxeter groups	[math]\displaystyle{ {\overline{HP}}_3 }[/math], [5,3[3]]
Properties	Vertex-transitive, edge-transitive, quasiregular

The alternated order-5 hexagonal tiling honeycomb, h{6,3,5}, ↔ , has triangular tiling and icosahedron facets, with a truncated icosahedron vertex figure. It is a quasiregular honeycomb.

Cantic order-5 hexagonal tiling honeycomb

Cantic order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	h2{6,3,5}
Coxeter diagram	↔
Cells	h2{6,3} t{3,5} 40px r{5,3}
Faces	triangle {3} pentagon {5} hexagon {6}
Vertex figure	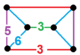triangular prism
Coxeter groups	[math]\displaystyle{ {\overline{HP}}_3 }[/math], [5,3[3]]
Properties	Vertex-transitive

The cantic order-5 hexagonal tiling honeycomb, h₂{6,3,5}, ↔ , has trihexagonal tiling, truncated icosahedron, and icosidodecahedron facets, with a triangular prism vertex figure.

Runcic order-5 hexagonal tiling honeycomb

Runcic order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	h3{6,3,5}
Coxeter diagram	↔
Cells	{3[3]} rr{5,3} 40px {5,3} 40px {}x{3}
Faces	triangle {3} square {4} pentagon {5}
Vertex figure	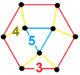triangular cupola
Coxeter groups	[math]\displaystyle{ {\overline{HP}}_3 }[/math], [5,3[3]]
Properties	Vertex-transitive

The runcic order-5 hexagonal tiling honeycomb, h₃{6,3,5}, ↔ , has triangular tiling, rhombicosidodecahedron, dodecahedron, and triangular prism facets, with a triangular cupola vertex figure.

Runcicantic order-5 hexagonal tiling honeycomb

Runcicantic order-5 hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	h2,3{6,3,5}
Coxeter diagram	↔
Cells	h2{6,3} tr{5,3} 40px t{5,3} 40px {}x{3}
Faces	triangle {3} square {4} hexagon {6} decagon {10}
Vertex figure	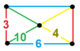rectangular pyramid
Coxeter groups	[math]\displaystyle{ {\overline{HP}}_3 }[/math], [5,3[3]]
Properties	Vertex-transitive

The runcicantic order-5 hexagonal tiling honeycomb, h_2,3{6,3,5}, ↔ , has trihexagonal tiling, truncated icosidodecahedron, truncated dodecahedron, and triangular prism facets, with a rectangular pyramid vertex figure.

See also

• Convex uniform honeycombs in hyperbolic space
• Regular tessellations of hyperbolic 3-space
• Paracompact uniform honeycombs

References

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
• Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapter 16-17: Geometries on Three-manifolds I, II)
• Norman Johnson Uniform Polytopes, Manuscript
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
  • N.W. Johnson: Geometries and Transformations, (2018) Chapter 13: Hyperbolic Coxeter groups