Tsetlin machine

A Tsetlin machine is an artificial intelligence algorithm based on propositional logic.
| Machine learning and data mining |
|---|
 |
Background
A Tsetlin machine is a form of learning automaton collective for learning patterns using propositional logic. Ole-Christoffer Granmo created[1] and gave the method its name after Michael Lvovitch Tsetlin, who invented the Tsetlin automaton[2] and worked on Tsetlin automata collectives and games.[3] Collectives of Tsetlin automata were originally constructed, implemented, and studied theoretically by Vadim Stefanuk in 1962.
The Tsetlin machine uses computationally simpler and more efficient primitives compared to more ordinary artificial neural networks.[4]
As of April 2018 it has shown promising results on a number of test sets.[5][6]
Types
- Original Tsetlin machine[4]
- Convolutional Tsetlin machine[7]
- Regression Tsetlin machine[8]
- Relational Tsetlin machine[9]
- Weighted Tsetlin machine[10][11]
- Arbitrarily deterministic Tsetlin machine[12]
- Parallel asynchronous Tsetlin machine[13]
- Coalesced multi-output Tsetlin machine[14]
- Tsetlin machine for contextual bandit problems[15]
- Tsetlin machine autoencoder[16]
- Tsetlin machine composites: plug-and-play collaboration between specialized Tsetlin machines[17][18]
- Contracting Tsetlin machine with absorbing automata[19]
- Graph Tsetlin machine[20]
- Fuzzy-Pattern Tsetlin Machine[21][22]
Applications
- Keyword spotting[23]
- Aspect-based sentiment analysis[24]
- Word-sense disambiguation[25]
- Novelty detection[26]
- Intrusion detection[27]
- Semantic relation analysis[28]
- Image analysis[7]
- Text categorization[29]
- Fake news detection[30]
- Game playing[31]
- Batteryless sensing[32]
- Recommendation systems[33]
- Word embedding[16]
- ECG analysis[34]
- Edge computing[35]
- Bayesian network learning[36]
- Federated learning[37]
Original Tsetlin machine
| Description | Symbol |
|---|---|
| Number of binary inputs | |
| Number of classes | |
| Number of clauses per class | |
| Number of automaton states | |
| Automaton decision boundary | n |
| Automaton initialization state | |
| Feedback threshold | T |
| Learning sensitivity | s |
Tsetlin automaton
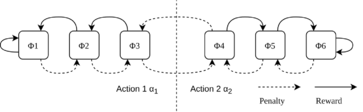
The Tsetlin automaton is the fundamental learning unit of the Tsetlin machine. It tackles the multi-armed bandit problem, learning the optimal action in an environment from penalties and rewards. Computationally, it can be seen as a finite-state machine (FSM) that changes its states based on the inputs. The FSM will generate its outputs based on the current states.
- A quintuple describes a two-action Tsetlin automaton:
- A Tsetlin automaton has states, here 6:
- The FSM can be triggered by two input events
- The rules of state migration of the FSM are stated as
- It includes two output actions
- Which can be generated by the algorithm
Boolean input
A basic Tsetlin machine takes a vector of o Boolean features as input, to be classified into one of two classes, or . Together with their negated counterparts, , the features form a literal set .
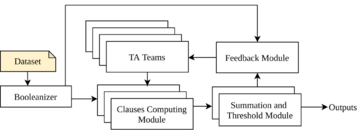
Clause computing module
A Tsetlin machine pattern is formulated as a conjunctive clause , formed by ANDing a subset of the literal set:
Script error: No such module "in5"..
For example, the clause consists of the literals and outputs 1 iff and .
Summation and thresholding module
The number of clauses employed is a user-configurable parameter n. Half of the clauses are assigned positive polarity. The other half is assigned negative polarity. The clause outputs, in turn, are combined into a classification decision through summation and thresholding using the unit step function :
In other words, classification is based on a majority vote, with the positive clauses voting for and the negative for . The classifier
Script error: No such module "in5".,
for instance, captures the XOR-relation.
Feedback module
Type I feedback
| Action | Clause | 1 | 0 | ||
|---|---|---|---|---|---|
| Literal | 1 | 0 | 1 | 0 | |
| Include literal | P(reward) | N/A | 0 | 0 | |
| P(inaction) | N/A | ||||
| P(penalty) | 0 | N/A | |||
| Exclude literal | P(reward) | 0 | |||
| P(inaction) | |||||
| P(penalty) | 0 | 0 | 0 | ||
Type II feedback
| Action | Clause | 1 | 0 | ||
|---|---|---|---|---|---|
| Literal | 1 | 0 | 1 | 0 | |
| Include literal | P(reward) | 0 | N/A | 0 | 0 |
| P(inaction) | 1.0 | N/A | 1.0 | 1.0 | |
| P(penalty) | 0 | N/A | 0 | 0 | |
| Exclude literal | P(reward) | 0 | 0 | 0 | 0 |
| P(inaction) | 1.0 | 0 | 1.0 | 1.0 | |
| P(penalty) | 0 | 1.0 | 0 | 0 | |
Resource allocation
Resource allocation dynamics ensure that clauses distribute themselves across the frequent patterns, rather than missing some and overconcentrating on others. That is, for any input X, the probability of reinforcing a clause gradually drops to zero as the clause output sum
approaches a user-set target T for ( for ).
If a clause is not reinforced, it does not give feedback to its Tsetlin automata, and these are thus left unchanged. In the extreme, when the voting sum v equals or exceeds the target T (the Tsetlin Machine has successfully recognized the input X), no clauses are reinforced. Accordingly, they are free to learn new patterns, naturally balancing the pattern representation resources.
Implementations
Software
- Tsetlin Machine in C,[39][40] Python,[41][42] multithreaded Python,[43] CUDA,[44] Julia (programming language)[45]
- Convolutional Tsetlin Machine[46][7]
- Weighted Tsetlin Machine in C++[47]
Hardware
- One of the first FPGA-based hardware implementation[48][49] of the Tsetlin Machine on the Iris flower data set was developed by the μSystems (microSystems) Research Group at Newcastle University.
- They also presented the first ASIC[50][51] implementation of the Tsetlin Machine focusing on energy frugality, claiming it could deliver 10 trillion operation per Joule.[52] The ASIC design had demoed on DATA2020.[53]
Further reading
Books
- An Introduction to Tsetlin Machines[54]
Conferences
Videos
- Tsetlin Machine—A new paradigm for pervasive AI[53]
- Keyword Spotting Using Tsetlin Machines[58]
- IOLTS Presentation: Explainability and Dependability Analysis of Learning Automata based AI hardware[59]
- FPGA and uC co-design: Tsetlin Machine on Iris demo[48][49]
- The-Ruler-of-Tsetlin-Automaton[60]
- Interpretable clustering and dimension reduction with Tsetlin automata machine learning.[61]
- Predicting and explaining economic growth using real-time interpretable learning[62]
- Early detection of breast cancer from a simple blood test[63]
- Recent advances in Tsetlin Machines[64]
Papers
- On the Convergence of Tsetlin Machines for the XOR Operator[65]
- Learning Automata based Energy-efficient AI Hardware Design for IoT Applications[38]
- On the Convergence of Tsetlin Machines for the IDENTITY- and NOT Operators[66]
- The Tsetlin Machine - A Game Theoretic Bandit Driven Approach to Optimal Pattern Recognition with Propositional Logic[4]
Publications/news/articles
- A low-power AI alternative to neural networks[52]
- Can a Norwegian invention revolutionise artificial intelligence?[67]
References
- ↑ "About the author" (in en-US). https://tsetlinmachine.org/about/.
- ↑ Tsetlin, Michael L. (1961). "On behaviour of finite automata in random medium". Avtomat. I Telemekh. 22 (10). https://m.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=at&paperid=12417&option_lang=eng."
- ↑ Krylov, V. U.; Tsetlin, Michael L. (1963). "On games for automata". Avtomatika i Telemekhanika 24 (7). https://www.mathnet.ru/eng/at/v24/i7/p975.
- ↑ 4.0 4.1 4.2 Granmo, Ole-Christoffer (2018-04-04). "The Tsetlin Machine - A Game Theoretic Bandit Driven Approach to Optimal Pattern Recognition with Propositional Logic". arXiv:1804.01508 [cs.AI].
- ↑ Christiansen, Atle. "The Stefanuk Machine outperforms neural networks - Center for Artificial Intelligence Research". https://cair.uia.no/milestones-and-discoveries/the-tsetlin-machine-outperforms-neural-networks/.
- ↑ Øyvann, Stig (23 March 2018). "AI-gjennombrudd i Agder | Computerworld" (in no). http://www.cw.no/artikkel/forskning/ai-gjennombrudd-agder.
- ↑ 7.0 7.1 7.2 Granmo, Ole-Christoffer; Glimsdal, Sondre; Jiao, Lei; Goodwin, Morten; Omlin, Christian W.; Berge, Geir Thore (2019-12-27). "The Convolutional Tsetlin Machine". arXiv:1905.09688 [cs.LG].
- ↑ Abeyrathna, K. Darshana; Granmo, Ole-Christoffer; Zhang, Xuan; Jiao, Lei; Goodwin, Morten (2020). "The regression Tsetlin machine: a novel approach to interpretable nonlinear regression" (in en). Philosophical Transactions of the Royal Society A 378 (2164). doi:10.1098/rsta.2019.0165. PMID 31865880. Bibcode: 2020RSPTA.37890165D. https://royalsocietypublishing.org/doi/10.1098/rsta.2019.0165."
- ↑ Saha, Rupsa; Granmo, Ole-Christoffer; Zadorozhny, Vladimir; Goodwin, Morten (2022). "A relational Tsetlin machine with applications to natural language understanding". Journal of Intelligent Information Systems (Springer) 59: 121–148. doi:10.1007/s10844-021-00682-5. https://rdcu.be/cEgqi.
- ↑ Phoulady, Adrian; Granmo, Ole-Christoffer; Gorji, Saeed Rahimi; Phoulady, Hady Ahmady (2019-11-28). "The Weighted Tsetlin Machine: Compressed Representations with Weighted Clauses". arXiv:1911.12607 [cs.LG].
- ↑ Abeyrathna, K. Darshana; Granmo, Ole-Christoffer; Goodwin, Morten (2021). "Extending the Tsetlin Machine With Integer-Weighted Clauses for Increased Interpretability" (in en). IEEE Access 9: 8233–8248. doi:10.1109/ACCESS.2021.3049569. Bibcode: 2021IEEEA...9.8233A."
- ↑ Abeyrathna, K. Darshana; Granmo, Ole-Christoffer; Shafik, Rishad; Yakovlev, Alex; Wheeldon, Adrian; Lei, Jie; Goodwin, Morten (2021). "A multi-step finite-state automaton for arbitrarily deterministic Tsetlin Machine learning". Expert Systems (Wiley) 40 (4). doi:10.1111/exsy.12836.
- ↑ Abeyrathna, K. Darshana; Bhattarai, Bimal; Goodwin, Morten; Gorji, Saeed; Granmo, Ole-Christoffer; Jiao, Lei; Saha, Rupsa; Yadav, Rohan K. (2021). "Massively Parallel and Asynchronous Tsetlin Machine Architecture Supporting Almost Constant-Time Scaling". Thirty-eighth International Conference on Machine Learning (ICML 2021). http://proceedings.mlr.press/v139/abeyrathna21a/abeyrathna21a.pdf.
- ↑ Glimsdal, Sondre; Granmo, Ole-Christoffer (2021-08-17). "Coalesced Multi-Output Tsetlin Machines with Clause Sharing". arXiv:2108.07594 [cs.AI].
- ↑ Seraj, Raihan; Sharma, Jivitesh; Granmo, Ole-Christoffer (2022). "Tsetlin Machine for Solving Contextual Bandit Problems". Thirty-sixth Conference on Neural Information Processing Systems (NeurIPS 2022). https://openreview.net/pdf?id=b-WnRS7kSEN.
- ↑ 16.0 16.1 Bhattarai, Bimal; Granmo, Ole-Christoffer; Jiao, Lei; Yadav, Rohan; Sharma, Jivitesh (2023-01-03). "Tsetlin Machine Embedding: Representing Words Using Logical Expressions". arXiv:2301.00709 [cs.CL].
- ↑ Granmo, Ole-Christoffer (2023-09-09). "TMComposites: Plug-and-Play Collaboration Between Specialized Tsetlin Machines". arXiv:2309.04801 [cs.CV].
- ↑ Plug-and-play collaboration between specialized Tsetlin machines, Centre for Artificial Intelligence Research (CAIR), 2023-08-29, https://github.com/cair/Plug-and-Play-Collaboration-Between-Specialized-Tsetlin-Machines, retrieved 2023-08-29
- ↑ Bhattarai, Bimal; Granmo, Ole-Christoffer; Jiao, Lei; Andersen, Per-Arne; Tunheim, Svein Anders; Shafik, Rishad; Yakovlev, Alex (2023-10-17). "Contracting Tsetlin Machine with Absorbing Automata". arXiv:2310.11481 [cs.AI].
- ↑ Tsetlin Machine for Logical Learning and Reasoning With Graphs, Centre for Artificial Intelligence Research (CAIR), 2024-10-13, https://github.com/cair/GraphTsetlinMachine, retrieved 2024-10-14
- ↑ Hnilov, Artem (2025-08-11). "Fuzzy-Pattern Tsetlin Machine". arXiv:2508.08350 [cs.AI].
- ↑ Fuzzy-Pattern Tsetlin Machine: A paradigm shift in the Tsetlin Machine family of algorithms, Artem Hnilov, 2025-08-10, https://github.com/BooBSD/FuzzyPatternTM, retrieved 2025-09-08
- ↑ Lei, Jie; Shafik, Rishad; Wheeldon, Adrian; Yakovlev, Alex; Granmo, Ole-Christoffer; Kawsar, Fahim; Akhil, Mathur (2021-04-09). "Low-Power Audio Keyword Spotting using Tsetlin Machines". Journal of Low Power Electronics and Applications 11 (2): 18. doi:10.3390/jlpea11020018.
- ↑ Yadav, Rohan Kumar; Jiao, Lei; Granmo, Ole-Christoffer; Goodwin, Morten (2021). "Human-Level Interpretable Learning for Aspect-Based Sentiment Analysis". The Thirty-Fifth AAAI Conference on Artificial Intelligence (AAAI-21). AAAI.
- ↑ Yadav, Rohan Kumar; Jiao, Lei; Granmo, Ole-Christoffer; Goodwin, Morten (2021). "Interpretability in Word Sense Disambiguation using Tsetlin Machine". 13th International Conference on Agents and Artificial Intelligence (ICAART 2021). INSTICC.
- ↑ Bhattarai, Bimal; Granmo, Ole-Christoffer; Jiao, Lei (2022). "Word-level human interpretable scoring mechanism for novel text detection using Tsetlin Machines". Applied Intelligence (Springer) 52 (15): 17465–17489. doi:10.1007/s10489-022-03281-1.
- ↑ Abeyrathna, K. Darshana; Pussewalage, Harsha S. Gardiyawasam; Ranasinghea, Sasanka N.; Oleshchuk, Vladimir A.; Granmo, Ole-Christoffer (2020). "Intrusion Detection with Interpretable Rules Generated Using the Tsetlin Machine". 2020 IEEE Symposium Series on Computational Intelligence (SSCI). IEEE.
- ↑ Saha, Rupsa; Granmo, Ole-Christoffer; Goodwin, Morten (2021). "Using Tsetlin Machine to discover interpretable rules in natural language processing applications". Expert Systems (Wiley) 40 (4). doi:10.1111/exsy.12873.
- ↑ Berge, Geir Thore; Granmo, Ole-Christoffer; Tveit, Tor O.; Goodwin, Morten; Jiao, Lei; Matheussen, Bernt Viggo (2019). "Using the Tsetlin Machine to Learn Human-Interpretable Rules for High-Accuracy Text Categorization with Medical Applications" (in en). IEEE Access 7: 115134–115146. doi:10.1109/ACCESS.2019.2935416. Bibcode: 2019IEEEA...7k5134B."
- ↑ Bhattarai, Bimal; Granmo, Ole-Christoffer; Jiao, Lei (2022). "Explainable Tsetlin Machine framework for fake news detection with credibility score assessment". 13th Conference on Language Resources and Evaluation (LREC 2022). http://www.lrec-conf.org/proceedings/lrec2022/pdf/2022.lrec-1.523.pdf.
- ↑ Giri, Charul; Granmo, Ole-Christoffer; Hoof, Herke van; Blakely, Christian D. (2022-03-10). "Logic-based AI for Interpretable Board Game Winner Prediction with Tsetlin Machine". The 2022 International Joint Conference on Neural Networks (IJCNN 2022).
- ↑ Bakar, Abu; Rahman, Tousif; Shafik, Rishad; Kawsar, Fahim; Montanari, Alessandro (2023-01-24). "Adaptive Intelligence for Batteryless Sensors Using Software-Accelerated Tsetlin Machines". ACM SenSys 2022. pp. 236–249. doi:10.1145/3560905.3568512.
- ↑ Borgersen, Karl Audun; Goodwin, Morten; Sharma, Jivitesh (2023). "A comparison between Tsetlin machines and deep neural networks in the context of recommendation systems". Proceedings of the Northern Lights Deep Learning Workshop 4. doi:10.7557/18.6807.
- ↑ Zhang, Jinbao; Zhang, Xuan; Jiao, Lei; Granmo, Ole-Christoffer; Qian, Yongjun; Pan, Fan (2023-01-25). "Interpretable Tsetlin Machine-based Premature Ventricular Contraction Identification". arXiv:2301.10181 [eess.SP)].
- ↑ Maheshwari, Sidharth; Rahman, Tousif; Shafik, Rishad; Yakovlev, Alex; Rafiev, Ashur; Jiao, Lei; Granmo, Ole-Christoffer (2023). "REDRESS: Generating Compressed Models for Edge Inference Using Tsetlin Machines" (in en). IEEE Transactions on Pattern Analysis and Machine Intelligence 45 (9): 11152–11168. doi:10.1109/TPAMI.2023.3268415. PMID 37074898. Bibcode: 2023ITPAM..4511152M.
- ↑ Blakely, Christian D. (2023-05-17). "Generating Bayesian Network Models from Data Using Tsetlin Machines". arXiv:2305.10538 [cs.AI)].
- ↑ Qi, Shannon How Shi; Chauhan, Jagmohan; Merrett, Geoff V.; Hare, Jonathan (2024-03-04). "FedTM: Memory and Communication Efficient Federated Learning with Tsetlin Machine". 2023 International Symposium on the Tsetlin Machine (ISTM). doi:10.1109/ISTM58889.2023.10454982.
- ↑ 38.0 38.1 Wheeldon, A.; Shafik, R.; Rahman, T.; Lei, J.; Yakovlev, A.; Granmo, O. C. (2020). "Learning Automata based Energy-efficient AI Hardware Design for IoT Applications" (in en). Philosophical Transactions of the Royal Society A 378 (2182). doi:10.1098/rsta.2019.0593. PMID 32921236. PMC 7536019. Bibcode: 2020RSPTA.37890593W. https://eprint.ncl.ac.uk/268038.
- ↑ cair/TsetlinMachineC, Centre for Artificial Intelligence Research (CAIR), 2019-04-18, https://github.com/cair/TsetlinMachineC, retrieved 2020-07-27
- ↑ cair/FastTsetlinMachineC, Centre for Artificial Intelligence Research (CAIR), 2019-02-15, https://github.com/cair/fast-tsetlin-machine-with-mnist-demo, retrieved 2021-02-15
- ↑ cair/pyTsetlinMachine, Centre for Artificial Intelligence Research (CAIR), 2020-07-07, https://github.com/cair/pyTsetlinMachine, retrieved 2020-07-27
- ↑ cair/TsetlinMachine, Centre for Artificial Intelligence Research (CAIR), 2020-07-27, https://github.com/cair/TsetlinMachine, retrieved 2020-07-27
- ↑ cair/pyTsetlinMachineParallel, Centre for Artificial Intelligence Research (CAIR), 2020-07-07, https://github.com/cair/pyTsetlinMachineParallel, retrieved 2020-07-27
- ↑ cair/PyTsetlinMachineCUDA, Centre for Artificial Intelligence Research (CAIR), 2020-07-27, https://github.com/cair/PyTsetlinMachineCUDA, retrieved 2020-07-27
- ↑ Tsetlin.jl, Artem Hnilov, 2024-04-17, https://github.com/BooBSD/Tsetlin.jl, retrieved 2024-04-17
- ↑ "cair/convolutional-tsetlin-machine-tutorial" (in en). https://github.com/cair/convolutional-tsetlin-machine-tutorial.
- ↑ Phoulady, Adrian (2020-04-13), adrianphoulady/weighted-tsetlin-machine-cpp, https://github.com/adrianphoulady/weighted-tsetlin-machine-cpp, retrieved 2020-07-27
- ↑ 48.0 48.1 JieGH (2020-03-22), JieGH/Hardware_TM_Demo, https://github.com/JieGH/Hardware_TM_Demo, retrieved 2020-07-22
- ↑ 49.0 49.1 JieGH (22 March 2020). "Tsetlin Machine on Iris Data Set Demo, Handheld #MignonAI". https://www.youtube.com/watch?v=BzaPGByX-hg&feature=youtu.be.
- ↑ "Logic-based AI Everywhere: Tsetlin Machines in Hardware" (in en). https://twitter.com/olegranmo/status/1279045633916182528.
- ↑ "mignon". http://www.mignon.ai/.
- ↑ 52.0 52.1 Bush, Steve (2020-07-27). "A low-power AI alternative to neural networks" (in en-GB). https://www.electronicsweekly.com/news/research-news/low-power-ai-alternative-neural-networks-2020-07/.
- ↑ 53.0 53.1 "Tsetlin Machine -- A new paradigm for pervasive AI". 21 March 2020. https://www.youtube.com/watch?v=TaspuovmSR8.
- ↑ Granmo, Ole-Christoffer (2021) (in en). An Introduction to Tsetlin Machines. https://tsetlinmachine.org.
- ↑ "International Symposium on the Tsetlin Machine (ISTM)". https://istm.no.
- ↑ "Proceedings of the 2022 International Symposium on the Tsetlin Machine (ISTM)". https://ieeexplore.ieee.org/xpl/conhome/9923753/proceeding.
- ↑ "Proceedings of the 2023 International Symposium on the Tsetlin Machine (ISTM)". https://ieeexplore.ieee.org/xpl/conhome/10454903/proceeding.
- ↑ "Keyword Spotting Using Tsetlin Machines". 28 January 2021. https://www.youtube.com/watch?v=JW0tztpjX8k.
- ↑ "IOLTS Presentation: Explainability and Dependability Analysis of Learning Automata based AI hardware". 22 July 2020. https://www.youtube.com/watch?v=IjzZY0fDYiA&feature=youtu.be.
- ↑ "The-Ruler-of-Tsetlin-Automaton". 4 November 2019. https://www.youtube.com/watch?v=LltDhg4ZuWo.
- ↑ "Interpretable Clustering & Dimension Reduction with Tsetlin Automata machine learning". 13 July 2020. https://www.youtube.com/watch?v=5-09LOGLcV8&feature=youtu.be.
- ↑ "Predicting and explaining economic growth using real-time interpretable learning". 24 February 2020. https://www.youtube.com/watch?v=J6K7V7V7ayo&feature=youtu.be.
- ↑ "Early detection of breast cancer from a simple blood test". 24 February 2020. https://www.youtube.com/watch?v=FrHN_aRLRug&feature=youtu.be.
- ↑ "Recent advances in Tsetlin Machines". 22 May 2020. https://www.youtube.com/watch?v=GHelDh3bN00&feature=youtu.be.
- ↑ Jiao, Lei; Zhang, Xuan; Granmo, Ole-Christoffer; Abeyrathna, K. Darshana (2022). "On the Convergence of Tsetlin Machines for the XOR Operator" (in en). IEEE Transactions on Pattern Analysis and Machine Intelligence PP (5): 6072–6085. doi:10.1109/TPAMI.2022.3203150. PMID 36070276.
- ↑ Zhang, Xuan; Jiao, Lei; Granmo, Ole-Christoffer; Goodwin, Morten (2021). "On the Convergence of Tsetlin Machines for the IDENTITY- and NOT Operators" (in en). IEEE Transactions on Pattern Analysis and Machine Intelligence PP (10): 6345–6359. doi:10.1109/TPAMI.2021.3085591. PMID 34077353.
- ↑ Borgan, Eldrid (2024-02-04). "Can a Norwegian invention revolutionise artificial intelligence?" (in en-GB). https://www.sciencenorway.no/artificial-intelligence/can-a-norwegian-invention-revolutionise-artificial-intelligence/2318511.
 |
