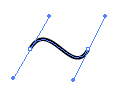
Bézier curve
A Bézier curve (/ˈbɛz.i.eɪ/ BEH-zee-ay)[1] is a parametric curve used in computer graphics and related fields.[2] A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape that otherwise has no mathematical representation or whose representation is unknown or too complicated. The Bézier curve is named after France engineer Pierre Bézier (1910–1999), who used it in the 1960s for designing curves for the bodywork of Renault cars.[3] Other uses include the design of computer fonts and animation.[3] Bézier curves can be combined to form a Bézier spline, or generalized to higher dimensions to form Bézier surfaces.[3] The Bézier triangle is a special case of the latter.
In vector graphics, Bézier curves are used to model smooth curves that can be scaled indefinitely. "Paths", as they are commonly referred to in image manipulation programs,[note 1] are combinations of linked Bézier curves. Paths are not bound by the limits of rasterized images and are intuitive to modify.
Bézier curves are also used in the time domain, particularly in animation,[4][note 2] user interface design and smoothing cursor trajectory in eye gaze controlled interfaces.[5] For example, a Bézier curve can be used to specify the velocity over time of an object such as an icon moving from A to B, rather than simply moving at a fixed number of pixels per step. When animators or interface designers talk about the "physics" or "feel" of an operation, they may be referring to the particular Bézier curve used to control the velocity over time of the move in question.
This also applies to robotics where the motion of a welding arm, for example, should be smooth to avoid unnecessary wear.
Invention
The mathematical basis for Bézier curves—the Bernstein polynomials—was established in 1912, but the polynomials were not applied to graphics until some 50 years later when mathematician Paul de Casteljau in 1959 developed de Casteljau's algorithm, a numerically stable method for evaluating the curves, and became the first to apply them to computer-aided design at French automaker Citroën.[6] De Casteljau's method was patented in France but not published until the 1980s[7] while the Bézier polynomials were widely publicised in the 1960s by the France engineer Pierre Bézier, who discovered them independently and used them to design automobile bodies at Renault.
Specific cases
A Bézier curve is defined by a set of control points P0 through Pn, where n is called the order of the curve (n = 1 for linear, 2 for quadratic, 3 for cubic, etc.). The first and last control points are always the endpoints of the curve; however, the intermediate control points generally do not lie on the curve. The sums in the following sections are to be understood as affine combinations – that is, the coefficients sum to 1.
Linear Bézier curves
Given distinct points P0 and P1, a linear Bézier curve is simply a line between those two points. The curve is given by
- [math]\displaystyle{ \mathbf{B}(t)=\mathbf{P}_0 + t(\mathbf{P}_1-\mathbf{P}_0)=(1-t)\mathbf{P}_0 + t\mathbf{P}_1,\ 0 \le t \le 1 }[/math]
This is the simplest and is equivalent to linear interpolation.[8] The quantity [math]\displaystyle{ \mathbf{P}_1-\mathbf{P}_0 }[/math] represents the displacement vector from the start point to the end point.
Quadratic Bézier curves
A quadratic Bézier curve is the path traced by the function B(t), given points P0, P1, and P2,
- [math]\displaystyle{ \mathbf{B}(t) = (1 - t)[(1 - t) \mathbf P_0 + t \mathbf P_1] + t [(1 - t) \mathbf P_1 + t \mathbf P_2],\ 0 \le t \le 1 }[/math],
which can be interpreted as the linear interpolant of corresponding points on the linear Bézier curves from P0 to P1 and from P1 to P2 respectively. Rearranging the preceding equation yields:
- [math]\displaystyle{ \mathbf{B}(t) = (1 - t)^{2}\mathbf{P}_0 + 2(1 - t)t\mathbf{P}_1 + t^{2}\mathbf{P}_2,\ 0 \le t \le 1. }[/math]
This can be written in a way that highlights the symmetry with respect to P1:
- [math]\displaystyle{ \mathbf{B}(t) = \mathbf{P}_1+(1 - t)^{2}(\mathbf{P}_0 - \mathbf{P}_1) + t^{2}(\mathbf{P}_2-\mathbf{P}_1),\ 0 \le t \le 1. }[/math]
Which immediately gives the derivative of the Bézier curve with respect to t:
- [math]\displaystyle{ \mathbf{B}'(t) = 2 (1 - t) (\mathbf{P}_1 - \mathbf{P}_0) + 2 t (\mathbf{P}_2 - \mathbf{P}_1), }[/math]
from which it can be concluded that the tangents to the curve at P0 and P2 intersect at P1. As t increases from 0 to 1, the curve departs from P0 in the direction of P1, then bends to arrive at P2 from the direction of P1.
The second derivative of the Bézier curve with respect to t is
- [math]\displaystyle{ \mathbf{B}''(t) = 2(\mathbf{P}_2 - 2 \mathbf{P}_1 + \mathbf{P}_0). }[/math]
Cubic Bézier curves
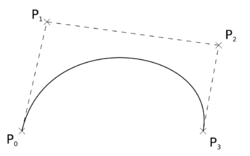
Four points P0, P1, P2 and P3 in the plane or in higher-dimensional space define a cubic Bézier curve. The curve starts at P0 going toward P1 and arrives at P3 coming from the direction of P2. Usually, it will not pass through P1 or P2; these points are only there to provide directional information. The distance between P1 and P2 determines "how far" and "how fast" the curve moves towards P1 before turning towards P2.
Writing BPi,Pj,Pk(t) for the quadratic Bézier curve defined by points Pi, Pj, and Pk, the cubic Bézier curve can be defined as an affine combination of two quadratic Bézier curves:
- [math]\displaystyle{ \mathbf{B}(t) = (1-t)\mathbf{B}_{\mathbf P_0,\mathbf P_1,\mathbf P_2}(t) + t \mathbf{B}_{\mathbf P_1,\mathbf P_2,\mathbf P_3}(t),\ 0 \le t \le 1. }[/math]
The explicit form of the curve is:
- [math]\displaystyle{ \mathbf{B}(t) = (1-t)^3\mathbf{P}_0+3(1-t)^2t\mathbf{P}_1+3(1-t)t^2\mathbf{P}_2+t^3\mathbf{P}_3,\ 0 \le t \le 1. }[/math]
For some choices of P1 and P2 the curve may intersect itself, or contain a cusp.
Any series of 4 distinct points can be converted to a cubic Bézier curve that goes through all 4 points in order. Given the starting and ending point of some cubic Bézier curve, and the points along the curve corresponding to t = 1/3 and t = 2/3, the control points for the original Bézier curve can be recovered.[9]
The derivative of the cubic Bézier curve with respect to t is
- [math]\displaystyle{ \mathbf{B}'(t) = 3(1-t)^2(\mathbf{P}_1 - \mathbf{P}_0) + 6(1-t)t(\mathbf{P}_2 - \mathbf{P}_1) + 3t^2(\mathbf{P}_3 - \mathbf{P}_2) \,. }[/math]
The second derivative of the Bézier curve with respect to t is
- [math]\displaystyle{ \mathbf{B}''(t) = 6(1-t)(\mathbf{P}_2 - 2 \mathbf{P}_1 + \mathbf{P}_0) + 6t(\mathbf{P}_3 - 2 \mathbf{P}_2 + \mathbf{P}_1) \,. }[/math]
General definition
Bézier curves can be defined for any degree n.
Recursive definition
A recursive definition for the Bézier curve of degree n expresses it as a point-to-point linear combination (linear interpolation) of a pair of corresponding points in two Bézier curves of degree n − 1.
Let [math]\displaystyle{ \mathbf{B}_{\mathbf{P}_0\mathbf{P}_1\ldots\mathbf{P}_k} }[/math] denote the Bézier curve determined by any selection of points P0, P1, ..., Pk. Then to start,
- [math]\displaystyle{ \mathbf{B}_{\mathbf{P}_0}(t) = \mathbf{P}_0 \text{, and} }[/math]
- [math]\displaystyle{ \mathbf{B}(t) = \mathbf{B}_{\mathbf{P}_0\mathbf{P}_1\ldots\mathbf{P}_n}(t) = (1-t)\mathbf{B}_{\mathbf{P}_0\mathbf{P}_1\ldots\mathbf{P}_{n-1}}(t) + t\mathbf{B}_{\mathbf{P}_1\mathbf{P}_2\ldots\mathbf{P}_n}(t) }[/math]
This recursion is elucidated in the animations below.
Explicit definition
The formula can be expressed explicitly as follows (where t0 and (1-t)0 are extended continuously to be 1 throughout [0,1]):
- [math]\displaystyle{ \begin{align} \mathbf{B}(t) &= \sum_{i=0}^n {n\choose i}(1 - t)^{n - i}t^i\mathbf{P}_i \\ &=(1 - t)^n\mathbf{P}_0 + {n\choose 1}(1 - t)^{n - 1}t\mathbf{P}_1 + \cdots + {n\choose n - 1}(1 - t)t^{n - 1}\mathbf{P}_{n - 1} + t^n\mathbf{P}_n, && 0 \leqslant t \leqslant 1 \end{align} }[/math]
where [math]\displaystyle{ \scriptstyle {n \choose i} }[/math] are the binomial coefficients.
For example, when n = 5:
- [math]\displaystyle{ \begin{align} \mathbf{B}(t) &= (1 - t)^5\mathbf{P}_0 + 5t(1 - t)^4\mathbf{P}_1 + 10t^2(1 - t)^3 \mathbf{P}_2 + 10t^3 (1-t)^2 \mathbf{P}_3 + 5t^4(1-t) \mathbf{P}_4 + t^5 \mathbf{P}_5, && 0 \leqslant t \leqslant 1. \end{align} }[/math]
Terminology
Some terminology is associated with these parametric curves. We have
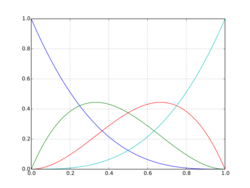
- [math]\displaystyle{ \mathbf{B}(t) = \sum_{i=0}^n b_{i, n}(t)\mathbf{P}_i,\ \ \ 0 \le t \le 1 }[/math]
where the polynomials
- [math]\displaystyle{ b_{i,n}(t) = {n \choose i} t^i (1 - t)^{n - i},\ \ \ i = 0, \ldots, n }[/math]
are known as Bernstein basis polynomials of degree n.
t0 = 1, (1 − t)0 = 1, and the binomial coefficient, [math]\displaystyle{ \scriptstyle {n \choose i} }[/math], is:
- [math]\displaystyle{ {n \choose i} = \frac{n!}{i!(n - i)!}. }[/math]
The points Pi are called control points for the Bézier curve. The polygon formed by connecting the Bézier points with lines, starting with P0 and finishing with Pn, is called the Bézier polygon (or control polygon). The convex hull of the Bézier polygon contains the Bézier curve.
Polynomial form
Sometimes it is desirable to express the Bézier curve as a polynomial instead of a sum of less straightforward Bernstein polynomials. Application of the binomial theorem to the definition of the curve followed by some rearrangement will yield
- [math]\displaystyle{ \mathbf{B}(t) = \sum_{j = 0}^n {t^j \mathbf{C}_j} }[/math]
where
- [math]\displaystyle{ \mathbf{C}_j = \frac{n!}{(n - j)!} \sum_{i = 0}^j \frac{(-1)^{i + j} \mathbf{P}_i}{i! (j - i)!} = \prod_{m = 0}^{j - 1} (n - m) \sum_{i = 0}^j \frac{(-1)^{i + j} \mathbf{P}_i}{i! (j - i)!}. }[/math]
This could be practical if [math]\displaystyle{ \mathbf{C}_j }[/math] can be computed prior to many evaluations of [math]\displaystyle{ \mathbf{B}(t) }[/math]; however one should use caution as high order curves may lack numeric stability (de Casteljau's algorithm should be used if this occurs). Note that the empty product is 1.
Properties
- The curve begins at [math]\displaystyle{ \mathbf P_0 }[/math] and ends at [math]\displaystyle{ \mathbf P_n }[/math]; this is the so-called endpoint interpolation property.
- The curve is a line if and only if all the control points are collinear.
- The start and end of the curve is tangent to the first and last section of the Bézier polygon, respectively.
- A curve can be split at any point into two subcurves, or into arbitrarily many subcurves, each of which is also a Bézier curve.
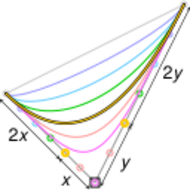
- Some curves that seem simple, such as the circle, cannot be described exactly by a Bézier or piecewise Bézier curve; though a four-piece cubic Bézier curve can approximate a circle (see composite Bézier curve), with a maximum radial error of less than one part in a thousand, when each inner control point (or offline point) is the distance [math]\displaystyle{ \textstyle\frac{4\left(\sqrt {2}-1\right)}{3} }[/math] horizontally or vertically from an outer control point on a unit circle. More generally, an n-piece cubic Bézier curve can approximate a circle, when each inner control point is the distance [math]\displaystyle{ \textstyle\frac{4}{3}\tan(t/4) }[/math] from an outer control point on a unit circle, where [math]\displaystyle{ t = 2\pi/n }[/math] (i.e. [math]\displaystyle{ t=360^\circ/n }[/math]), and [math]\displaystyle{ n\gt 2 }[/math].
- Every quadratic Bézier curve is also a cubic Bézier curve, and more generally, every degree n Bézier curve is also a degree m curve for any m > n. In detail, a degree n curve with control points [math]\displaystyle{ \mathbf{P}_0,\,\dots,\,\mathbf{P}_n }[/math] is equivalent (including the parametrization) to the degree n + 1 curve with control points [math]\displaystyle{ \mathbf{P}'_0,\,\dots,\,\mathbf {P}'_{n+1} }[/math], where [math]\displaystyle{ \mathbf P'_k=\tfrac{k}{n+1}\mathbf P_{k-1}+\left(1-\tfrac{k}{n+1}\right)\mathbf P_k }[/math], [math]\displaystyle{ \forall k = 0,\,1,\,\dots,\,n,\,n+1 }[/math] and define [math]\displaystyle{ \mathbf{P}_{n+1} := \mathbf{P}_{0} }[/math], [math]\displaystyle{ \mathbf{P}_{-1} := \mathbf{P}_{n} }[/math].
- Bézier curves have the variation diminishing property. What this means in intuitive terms is that a Bézier curve does not "undulate" more than the polygon of its control points, and may actually "undulate" less than that.[10]
- There is no local control in degree n Bézier curves—meaning that any change to a control point requires recalculation of and thus affects the aspect of the entire curve, "although the further that one is from the control point that was changed, the smaller is the change in the curve."[11]
- A Bézier curve of order higher than two may intersect itself or have a cusp for certain choices of the control points.
Second-order curve is a parabolic segment
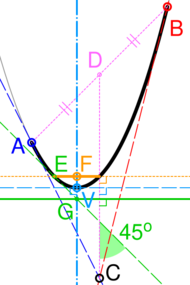
A quadratic Bézier curve is also a segment of a parabola. As a parabola is a conic section, some sources refer to quadratic Béziers as "conic arcs".[12] With reference to the figure on the right, the important features of the parabola can be derived as follows:[13]
- Tangents to the parabola at the endpoints of the curve (A and B) intersect at its control point (C).
- If D is the midpoint of AB, the tangent to the curve which is perpendicular to CD (dashed cyan line) defines its vertex (V). Its axis of symmetry (dash-dot cyan) passes through V and is perpendicular to the tangent.
- E is either point on the curve with a tangent at 45° to CD (dashed green). If G is the intersection of this tangent and the axis, the line passing through G and perpendicular to CD is the directrix (solid green).
- The focus (F) is at the intersection of the axis and a line passing through E and perpendicular to CD (dotted yellow). The latus rectum is the line segment within the curve (solid yellow).
Derivative
The derivative for a curve of order n is
- [math]\displaystyle{ \mathbf{B}'(t) = n \sum_{i=0}^{n-1} b_{i,n-1}(t) (\mathbf{P}_{i+1} - \mathbf{P}_i). }[/math]
Constructing Bézier curves
Linear curves
Let t denote the fraction of progress (from 0 to 1) the point B(t) has made along its traversal from P0 to P1. For example, when t=0.25, B(t) is one quarter of the way from point P0 to P1. As t varies from 0 to 1, B(t) draws a line from P0 to P1.
![Animation of a linear Bézier curve, t in [0,1]](/wiki/images/thumb/0/00/B%C3%A9zier_1_big.gif/240px-B%C3%A9zier_1_big.gif)
|
| Animation of a linear Bézier curve, t in [0,1] |
Quadratic curves
For quadratic Bézier curves one can construct intermediate points Q0 and Q1 such that as t varies from 0 to 1:
- Point Q0(t) varies from P0 to P1 and describes a linear Bézier curve.
- Point Q1(t) varies from P1 to P2 and describes a linear Bézier curve.
- Point B(t) is interpolated linearly between Q0(t) to Q1(t) and describes a quadratic Bézier curve.
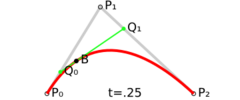 |
![Animation of a quadratic Bézier curve, t in [0,1]](/wiki/images/thumb/3/3d/B%C3%A9zier_2_big.gif/240px-B%C3%A9zier_2_big.gif)
| |
| Construction of a quadratic Bézier curve | Animation of a quadratic Bézier curve, t in [0,1] |
Higher-order curves
For higher-order curves one needs correspondingly more intermediate points. For cubic curves one can construct intermediate points Q0, Q1, and Q2 that describe linear Bézier curves, and points R0 and R1 that describe quadratic Bézier curves:
 |
![Animation of a cubic Bézier curve, t in [0,1]](/wiki/images/thumb/d/db/B%C3%A9zier_3_big.gif/240px-B%C3%A9zier_3_big.gif)
| |
| Construction of a cubic Bézier curve | Animation of a cubic Bézier curve, t in [0,1] |
For fourth-order curves one can construct intermediate points Q0, Q1, Q2 and Q3 that describe linear Bézier curves, points R0, R1 and R2 that describe quadratic Bézier curves, and points S0 and S1 that describe cubic Bézier curves:
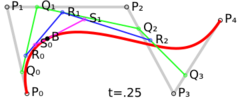 |
![Animation of a quartic Bézier curve, t in [0,1]](/wiki/images/thumb/a/a4/B%C3%A9zier_4_big.gif/240px-B%C3%A9zier_4_big.gif)
| |
| Construction of a quartic Bézier curve | Animation of a quartic Bézier curve, t in [0,1] |
For fifth-order curves, one can construct similar intermediate points.
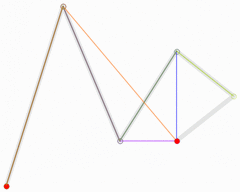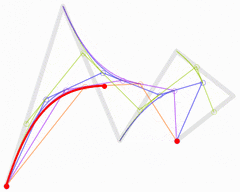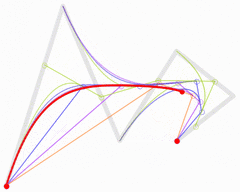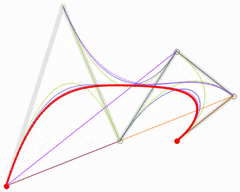
|
| Animation of a fifth-order Bézier curve, t in [0,1] in red. The Bézier curves for each of the lower orders are also shown. |
These representations rest on the process used in De Casteljau's algorithm to calculate Bézier curves.[14]
Offsets (or stroking) of Bézier curves
The curve at a fixed offset from a given Bézier curve, called an offset or parallel curve in mathematics (lying "parallel" to the original curve, like the offset between rails in a railroad track), cannot be exactly formed by a Bézier curve (except in some trivial cases). In general, the two-sided offset curve of a cubic Bézier is a 10th-order algebraic curve[15] and more generally for a Bézier of degree n the two-sided offset curve is an algebraic curve of degree 4n − 2.[16] However, there are heuristic methods that usually give an adequate approximation for practical purposes.[17]
In the field of vector graphics, painting two symmetrically distanced offset curves is called stroking (the Bézier curve or in general a path of several Bézier segments).[15] The conversion from offset curves to filled Bézier contours is of practical importance in converting fonts defined in Metafont, which require stroking of Bézier curves, to the more widely used PostScript type 1 fonts, which only require (for efficiency purposes) the mathematically simpler operation of filling a contour defined by (non-self-intersecting) Bézier curves.[18]
Degree elevation
A Bézier curve of degree n can be converted into a Bézier curve of degree n + 1 with the same shape. This is useful if software supports Bézier curves only of specific degree. For example, systems that can only work with cubic Bézier curves can implicitly work with quadratic curves by using their equivalent cubic representation.
To do degree elevation, we use the equality [math]\displaystyle{ \mathbf{B}(t) = (1-t)\mathbf{B}(t) + t\mathbf{B}(t). }[/math] Each component [math]\displaystyle{ \mathbf{b}_{i,n}(t)\mathbf{P}_i }[/math] is multiplied by (1 − t) and t, thus increasing a degree by one, without changing the value. Here is the example of increasing degree from 2 to 3.
- [math]\displaystyle{ \begin{align} (1 - t)^2 \mathbf{P}_0 + 2(1 - t)t\mathbf{P}_1 + t^2 \mathbf{P}_2 &= (1 - t)^3 \mathbf{P}_0 + 2(1 - t)^2 t\mathbf{P}_1 + (1 - t)t^2 \mathbf{P}_2 + (1 - t)^{2}t\mathbf{P}_0 + 2(1 - t)t^2 \mathbf{P}_1 + t^3 \mathbf{P}_2 \\ &= (1 - t)^3 \mathbf{P}_0 + (1 - t)^2 t \left( \mathbf{P}_0 + 2\mathbf{P}_1\right) + (1 - t) t^2 \left(2\mathbf{P}_1 + \mathbf{P}_2\right) + t^{3}\mathbf{P}_2 \\ &= (1 - t)^3 \mathbf{P}_0 + 3(1 - t)^2 t \tfrac{1}{3} \left( \mathbf{P}_0 + 2\mathbf{P}_1 \right) + 3(1 - t) t^2 \tfrac{1}{3} \left( 2\mathbf{P}_1 + \mathbf{P}_2 \right) + t^{3}\mathbf{P}_2 \end{align} }[/math]
For arbitrary n we use equalities
- [math]\displaystyle{ \begin{cases} {n + 1 \choose i}(1 - t)\mathbf{b}_{i, n} = {n \choose i} \mathbf{b}_{i, n + 1} \\ {n + 1 \choose i + 1} t\mathbf{b}_{i, n} = {n \choose i} \mathbf{b}_{i + 1, n + 1} \end{cases} \quad \implies \quad \begin{cases} (1 - t)\mathbf{b}_{i, n} = \frac{n + 1 - i}{n + 1} \mathbf{b}_{i, n + 1} \\ t\mathbf{b}_{i, n} = \frac{i + 1}{n + 1} \mathbf{b}_{i + 1, n + 1} \end{cases} }[/math]
Therefore:
- [math]\displaystyle{ \begin{align} \mathbf{B}(t) &= (1 - t)\sum_{i=0}^n \mathbf{b}_{i, n}(t)\mathbf{P}_i + t\sum_{i=0}^n \mathbf{b}_{i, n}(t)\mathbf{P}_i \\ &= \sum_{i=0}^n \frac{n + 1 - i}{n + 1}\mathbf{b}_{i, n + 1}(t)\mathbf{P}_i + \sum_{i=0}^n \frac{i + 1}{n + 1}\mathbf{b}_{i + 1, n + 1}(t)\mathbf{P}_i \\ &= \sum_{i=0}^{n + 1} \left(\frac{i}{n + 1}\mathbf{P}_{i - 1} + \frac{n + 1 - i}{n + 1}\mathbf{P}_i\right) \mathbf{b}_{i, n + 1}(t) \\ &= \sum_{i=0}^{n + 1} \mathbf{b}_{i, n + 1}(t)\mathbf{P'}_i \end{align} }[/math]
introducing arbitrary [math]\displaystyle{ \mathbf{P}_{-1} }[/math] and [math]\displaystyle{ \mathbf{P}_{n + 1} }[/math].
Therefore, new control points are[19]
- [math]\displaystyle{ \mathbf{P'}_i = \frac{i}{n + 1}\mathbf{P}_{i - 1} + \frac{n + 1 - i}{n + 1}\mathbf{P}_i,\quad i=0, \ldots, n + 1. }[/math]
Repeated degree elevation
The concept of degree elevation can be repeated on a control polygon R to get a sequence of control polygons R, R1, R2, and so on. After r degree elevations, the polygon Rr has the vertices P0,r, P1,r, P2,r, ..., Pn+r,r given by [19]
- [math]\displaystyle{ \mathbf{P}_{i,r} = \sum_{j=0}^n \mathbf{P}_j \tbinom nj \frac{\tbinom{r}{i-j}}{\tbinom{n+r}{i}}. }[/math]
It can also be shown that for the underlying Bézier curve B,
- [math]\displaystyle{ \mathbf{\lim_{r \to \infty}R_r} = \mathbf{B}. }[/math]
Rational Bézier curves
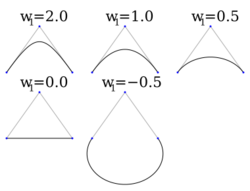
The rational Bézier curve adds adjustable weights to provide closer approximations to arbitrary shapes. The numerator is a weighted Bernstein-form Bézier curve and the denominator is a weighted sum of Bernstein polynomials. Rational Bézier curves can, among other uses, be used to represent segments of conic sections exactly, including circular arcs.[20]
Given n + 1 control points P0, ..., Pn, the rational Bézier curve can be described by
- [math]\displaystyle{ \mathbf{B}(t) = \frac{ \sum_{i=0}^n b_{i,n}(t) \mathbf{P}_{i}w_i } { \sum_{i=0}^n b_{i,n}(t) w_i }, }[/math]
or simply
- [math]\displaystyle{ \mathbf{B}(t) = \frac{ \sum_{i=0}^n {n \choose i} t^i (1-t)^{n-i}\mathbf{P}_{i}w_i } { \sum_{i=0}^n {n \choose i} t^i (1-t)^{n-i}w_i }. }[/math]
The expression can be extended by using number systems besides reals for the weights. In the complex plane the points {1}, {-1}, and {1} with weights {[math]\displaystyle{ i }[/math]}, {1}, and {[math]\displaystyle{ -i }[/math]} generate a full circle with radius one. For curves with points and weights on a circle, the weights can be scaled without changing the curve's shape.[21] Scaling the central weight of the above curve by 1.35508 gives a more uniform parameterization.
Applications
Computer graphics
Bézier curves are widely used in computer graphics to model smooth curves. As the curve is completely contained in the convex hull of its control points, the points can be graphically displayed and used to manipulate the curve intuitively. Affine transformations such as translation and rotation can be applied on the curve by applying the respective transform on the control points of the curve.
Quadratic and cubic Bézier curves are most common. Higher degree curves are more computationally expensive to evaluate. When more complex shapes are needed, low order Bézier curves are patched together, producing a composite Bézier curve. A composite Bézier curve is commonly referred to as a "path" in vector graphics languages (like PostScript), vector graphics standards (like SVG) and vector graphics programs (like Artline, Timeworks Publisher, Adobe Illustrator, CorelDraw, Inkscape, and Allegro). In order to join Bézier curves into a composite Bézier curve without kinks, a property called G1 continuity suffices to force the control point at which two constituent Bézier curves meet to lie on the line defined by the two control points on either side.

The simplest method for scan converting (rasterizing) a Bézier curve is to evaluate it at many closely spaced points and scan convert the approximating sequence of line segments. However, this does not guarantee that the rasterized output looks sufficiently smooth, because the points may be spaced too far apart. Conversely it may generate too many points in areas where the curve is close to linear. A common adaptive method is recursive subdivision, in which a curve's control points are checked to see if the curve approximates a line to within a small tolerance. If not, the curve is subdivided parametrically into two segments, 0 ≤ t ≤ 0.5 and 0.5 ≤ t ≤ 1, and the same procedure is applied recursively to each half. There are also forward differencing methods, but great care must be taken to analyse error propagation.[23]
Analytical methods where a Bézier is intersected with each scan line involve finding roots of cubic polynomials (for cubic Béziers) and dealing with multiple roots, so they are not often used in practice.[23]
The rasterisation algorithm used in Metafont is based on discretising the curve, so that it is approximated by a sequence of "rook moves" that are purely vertical or purely horizontal, along the pixel boundaries. To that end, the plane is first split into eight 45° sectors (by the coordinate axes and the two lines [math]\displaystyle{ y = \pm x }[/math]), then the curve is decomposed into smaller segments such that the direction of a curve segment stays within one sector; since the curve velocity is a second degree polynomial, finding the [math]\displaystyle{ t }[/math] values where it is parallel to one of these lines can be done by solving quadratic equations. Within each segment, either horizontal or vertical movement dominates, and the total number of steps in either direction can be read off from the endpoint coordinates; in for example the 0–45° sector horizontal movement to the right dominates, so it only remains to decide between which steps to the right the curve should make a step up.[24]
There is also a modified curve form of Bresenham's line drawing algorithm by Zingl that performs this rasterization by subdividing the curve into rational pieces and calculating the error at each pixel location such that it either travels at a 45° angle or straight depending on compounding error as it iterates through the curve. This reduces the next step calculation to a series of integer additions and subtractions.[25]
Animation
In animation applications, such as Adobe Flash and Synfig, Bézier curves are used to outline, for example, movement. Users outline the wanted path in Bézier curves, and the application creates the needed frames for the object to move along the path.[26][27]
In 3D animation, Bézier curves are often used to define 3D paths as well as 2D curves for keyframe interpolation.[28] Bézier curves are now very frequently used to control the animation easing in CSS, JavaScript, JavaFx and Flutter SDK.[4]
Fonts
TrueType fonts use composite Bézier curves composed of quadratic Bézier curves. Other languages and imaging tools (such as PostScript, Asymptote, Metafont, and SVG) use composite Béziers composed of cubic Bézier curves for drawing curved shapes. OpenType fonts can use either kind of curve, depending on which font technology underlies the OpenType wrapper.[29]
Font engines, like FreeType, draw the font's curves (and lines) on a pixellated surface using a process known as font rasterization.[12] Typically font engines and vector graphics engines render Bézier curves by splitting them recursively up to the point where the curve is flat enough to be drawn as a series of linear or circular segments. The exact splitting algorithm is implementation dependent, only the flatness criteria must be respected to reach the necessary precision and to avoid non-monotonic local changes of curvature. The "smooth curve" feature of charts in Microsoft Excel also uses this algorithm.[30]
Because arcs of circles and ellipses cannot be exactly represented by Bézier curves, they are first approximated by Bézier curves, which are in turn approximated by arcs of circles. This is inefficient as there exists also approximations of all Bézier curves using arcs of circles or ellipses, which can be rendered incrementally with arbitrary precision. Another approach, used by modern hardware graphics adapters with accelerated geometry, can convert exactly all Bézier and conic curves (or surfaces) into NURBS, that can be rendered incrementally without first splitting the curve recursively to reach the necessary flatness condition. This approach also preserves the curve definition under all linear or perspective 2D and 3D transforms and projections.[citation needed]
Robotics
Because the control polygon allows to tell whether or not the path collides with any obstacles, Bézier curves are used in producing trajectories of the end effectors.[31] Furthermore, joint space trajectories can be accurately differentiated using Bézier curves. Consequently, the derivatives of joint space trajectories are used in the calculation of the dynamics and control effort (torque profiles) of the robotic manipulator.[31]
See also
- Bézier surface
- B-spline
- GEM/4 and GEM/5
- Hermite curve
- NURBS
- String art – Bézier curves are also formed by many common forms of string art, where strings are looped across a frame of nails.[32]
- Variation diminishing property of Bézier curves
Notes
- ↑ Image manipulation programs such as Inkscape, Adobe Photoshop, and GIMP.
- ↑ In animation applications such as Adobe Flash, Adobe After Effects, Microsoft Expression Blend, Blender, Autodesk Maya and Autodesk 3ds Max.
References
Citations
- ↑ Wells, John (3 April 2008). Longman Pronunciation Dictionary (3rd ed.). Pearson Longman. ISBN 978-1-4058-8118-0.
- ↑ Mortenson, Michael E. (1999). Mathematics for Computer Graphics Applications. Industrial Press Inc.. p. 264. ISBN 9780831131111. https://books.google.com/books?id=YmQy799flPkC&pg=PA264.
- ↑ 3.0 3.1 3.2 Hazewinkel, Michiel (1997). Encyclopaedia of Mathematics: Supplement. 1. Springer Science & Business Media. p. 119. ISBN 9780792347095. https://books.google.com/books?id=3ndQH4mTzWQC&pg=PA119.
- ↑ 4.0 4.1 "Cubic class - animation library - Dart API". https://api.flutter.dev/flutter/animation/Cubic-class.html.
- ↑ Biswas, Pradipta; Langdon, Pat (2015-04-03). "Multimodal Intelligent Eye-Gaze Tracking System". International Journal of Human-Computer Interaction 31 (4): 277–294. doi:10.1080/10447318.2014.1001301. ISSN 1044-7318.
- ↑ Gerald E. Farin; Josef Hoschek; Myung-Soo Kim (2002). Handbook of Computer Aided Geometric Design. Elsevier. pp. 4–6. ISBN 978-0-444-51104-1. https://books.google.com/books?id=0SV5G8fgxLoC&pg=PA4.
- ↑ Paul de Casteljau. Mathématiques et CAO. Tome 2 : Formes à pôles. ISBN 9782866010423.
- ↑ Mario A. Gutiérrez; Frédéric Vexo; Daniel Thalmann (2023). Stepping into Virtual Reality. Springer Nature. p. 33. ISBN 9783031364877. https://books.google.com/books?id=Wq7QEAAAQBAJ&pg=PA33.
- ↑ John Burkardt. "Forcing Bezier Interpolation". http://people.sc.fsu.edu/~jburkardt/html/bezier_interpolation.html.
- ↑ Teofilo Gonzalez; Jorge Diaz-Herrera; Allen Tucker (2014). Computing Handbook, Third Edition: Computer Science and Software Engineering. CRC Press. page 32-14. ISBN 978-1-4398-9852-9. https://books.google.com/books?id=vMqSAwAAQBAJ&pg=SA32-PA14.
- ↑ Max K. Agoston (2005). Computer Graphics and Geometric Modelling: Implementation & Algorithms. Springer Science & Business Media. p. 404. ISBN 978-1-84628-108-2. https://books.google.com/books?id=TAYw3LEs5rgC&pg=PA404.
- ↑ 12.0 12.1 "FreeType Glyph Conventions / VI. FreeType outlines". 13 February 2018. http://www.freetype.org/freetype2/docs/glyphs/glyphs-6.html.
"FreeType Glyph Conventions – Version 2.1 / VI. FreeType outlines". 6 March 2011. http://www.freetype.org/freetype2/docs/glyphs/glyphs-6.html. - ↑ Duncan Marsh (2005). Applied Geometry for Computer Graphics and CAD. Springer Undergraduate Mathematics Series (2nd ed.). ASIN 1852338016. ISBN 978-1-85233-801-5.
- ↑ Shene, C. K.. "Finding a Point on a Bézier Curve: De Casteljau's Algorithm". http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/de-casteljau.html.
- ↑ 15.0 15.1 Mark Kilgard (April 10, 2012). "CS 354 Vector Graphics & Path Rendering". p. 28. http://www.slideshare.net/Mark_Kilgard/22pathrender.
- ↑ Rida T. Farouki. "Introduction to Pythagorean-hodograph curves". http://faculty.engineering.ucdavis.edu/farouki/wp-content/uploads/sites/41/2013/02/Introduction-to-PH-curves.pdf., particularly p. 16 "taxonomy of offset curves".
- ↑ For example: [1] or [2]. For a survey see [3].
- ↑ Richard J. Kinch (1995). "MetaFog: Converting Metafont shapes to contours". TUGboat 16 (3–Proceedings of the 1995 Annual Meeting). https://www.tug.org/TUGboat/tb16-3/tb48kinc.pdf.
- ↑ 19.0 19.1 Farin, Gerald (1997). Curves and surfaces for computer-aided geometric design (4 ed.). Elsevier Science & Technology Books. ISBN 978-0-12-249054-5.
- ↑ Neil Dodgson (2000-09-25). "Some Mathematical Elements of Graphics: Rational B-splines". http://www.cl.cam.ac.uk/teaching/2000/AGraphHCI/SMEG/node5.html.
- ↑ J. Sánchez-Reyes (November 2009). "Complex rational Bézier curves". Computer Aided Geometric Design 26 (8): 865–876. doi:10.1016/j.cagd.2009.06.003.
- ↑ Alexander Reshetov and David Luebke, Phantom Ray-Hair Intersector. In Proceedings of the ACM on Computer Graphics and Interactive Techniques (August 1, 2018). [4]
- ↑ 23.0 23.1 "Complex Quadratic Bézier Curve on Unit Circle". Zhengzhou, China: School of Software, Zhengzhou University. https://www.atlantis-press.com/php/download_paper.php?id=12403.
- ↑ Parts 19–22 of Knuth, Donald E. (1986). Metafont: The Program. Addison-Wesley. ISBN 0-201-13438-1.
- ↑ Zingl, Alois "A Rasterizing Algorithm for Drawing Curves" (2012) http://members.chello.at/~easyfilter/Bresenham.pdf
- ↑ "Using motion paths in animations". https://www.adobe.com/devnet/flash/learning_guide/animation/part07.html.
- ↑ "Following a Spline". https://wiki.synfig.org/Doc:Following_a_Spline.
- ↑ Dodgson, Neil A. (1999). "Advanced Graphics Lecture Notes". University of Cambridge Computer Laboratory. https://www.cl.cam.ac.uk/teaching/1213/AdvGraph/smeg13.pdf.
- ↑ "The difference between CFF and TTF". Linotype. https://www.linotype.com/8120/the-difference-between-cff-and-ttf.html. "The OpenType format was formulated in 1996. By 2003, it began to replace two competing formats: the Type1 fonts, developed by Adobe and based on [P]ost[S]cript, and the TrueType fonts, specified by Microsoft and Apple. (...) TTF stands for TrueTypeFont and indicates that the font data is the same as in the TrueType fonts. CFF stands for the Type1 font format. Strictly speaking, it refers to the Compact Font Format, which is used in the compression processes for the Type2 fonts. (...) the cubic Bézier format of the Type1 fonts is more space-saving compared to the quadratic format of the TrueType fonts. Some kilobytes can be saved in large, elaborate fonts which may represent an advantage on the Web. On the other hand, the more detailed hinting information of the TrueType fonts is useful for very extensive optimization for screen use."
- ↑ "smooth_curve_bezier_example_file.xls". http://www.xlrotor.com/resources/files.shtml.
- ↑ 31.0 31.1 Malik, Aryslan; Henderson, Troy; Prazenica, Richard (January 2021). "Trajectory Generation for a Multibody Robotic System using the Product of Exponentials Formulation". AIAA Scitech 2021 Forum: 2016. doi:10.2514/6.2021-2016. ISBN 978-1-62410-609-5. https://arc.aiaa.org/doi/abs/10.2514/6.2021-2016.
- ↑ Gross, Renan (2014). "Bridges, String Art, and Bézier Curves". in Pitici, Mircea. The Best Writing on Mathematics 2013. Princeton University Press. pp. 77–89. doi:10.1515/9781400847990-011. ISBN 9780691160412.
Sources
- Rida T. Farouki (August 2012). "The Bernstein polynomial basis: A centennial retrospective". Computer Aided Geometric Design 29 (6): 379–419. doi:10.1016/j.cagd.2012.03.001. http://mae.engr.ucdavis.edu/~farouki/bernstein.pdf.
- Paul Bourke (2009-07-19). Bézier Surfaces (in 3D). http://local.wasp.uwa.edu.au/~pbourke/geometry/bezier/index.html.
- Donald Knuth (1986). Metafont: the Program. Addison-Wesley. pp. 123–131. Excellent discussion of implementation details; available for free as part of the TeX distribution.
- Thomas Sederberg. Bézier curves. http://www.tsplines.com/resources/class_notes/Bezier_curves.pdf. Retrieved 2005-09-14.
- J. D. Foley (1992). Computer Graphics: Principles and Practice in C (2nd ed.). Addison Wesley.
- Rajiv Chandel (2014-03-20). "Implementing Bezier Curves in games". http://codingg.blogspot.in/2014/03/implementing-bezier-curves-in-games.html.
Further reading
- A Primer on Bézier Curves – an open source online book explaining Bézier curves and associated graphics algorithms, with interactive graphics
- Cubic Bezier Curves – Under the Hood (video) – video showing how computers render a cubic Bézier curve, by Peter Nowell
- From Bézier to Bernstein Feature Column from American Mathematical Society
- Hazewinkel, Michiel, ed. (2001), "Bézier curve", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/b110460
- Prautzsch, Hartmut; Boehm, Wolfgang; Paluszny, Marco (2002). Bézier and B-Spline Techniques. Springer Science & Business Media. ISBN 978-3-540-43761-1.
- Gallier, Jean (1999). "Chapter 5. Polynomial Curves as Bézier Curves". Curves and Surfaces in Geometric Modeling: Theory and Algorithms. Morgan Kaufmann. http://www.cis.upenn.edu/~jean/gbooks/geom1.html. This book is out of print and freely available from the author.
- Farin, Gerald E. (2002). Curves and Surfaces for CAGD: A Practical Guide (5th ed.). Morgan Kaufmann. ISBN 978-1-55860-737-8. http://www.farinhansford.com/books/cagd/.
- Weisstein, Eric W.. "Bézier Curve". http://mathworld.wolfram.com/BezierCurve.html.
- Hoffmann, Gernot. "Bézier Curves". http://www.fho-emden.de/~hoffmann/bezier18122002.pdf. (60 pages)
- Ahn, Young Joon (2004). "Approximation of circular arcs and offset curves by Bézier curves of high degree". Journal of Computational and Applied Mathematics 167 (2): 405–416. doi:10.1016/j.cam.2003.10.008. Bibcode: 2004JCoAM.167..405A.
- Davies, Jason. "Animated Bézier curves". https://www.jasondavies.com/animated-bezier/.
- Hovey, Chad (20 May 2022). "Bézier Geometry". https://github.com/sandialabs/sibl#documentation.
- Hovey, Chad (2022). Formulation and Python Implementation of Bézier and B-Spline Geometry. SAND2022-7702C. (153 pages)
External links
- Computer code
- TinySpline: Open source C-library for NURBS, B-splines and Bézier curves with bindings for various languages
- C++ library to generate Bézier functions at compile time
- Simple Bézier curve implementation via recursive method in Python
 |