Angular displacement

Rotation of a rigid body P about a fixed axis O.

Angular displacement of a body is the angle (in radians, degrees or turns) through which a point revolves around a centre or a specified axis in a specified sense. When a body rotates about its axis, the motion cannot simply be analyzed as a particle, as in circular motion it undergoes a changing velocity and acceleration at any time (t). When dealing with the rotation of a body, it becomes simpler to consider the body itself rigid. A body is generally considered rigid when the separations between all the particles remains constant throughout the body's motion, so for example parts of its mass are not flying off. In a realistic sense, all things can be deformable, however this impact is minimal and negligible. Thus the rotation of a rigid body over a fixed axis is referred to as rotational motion.

Example

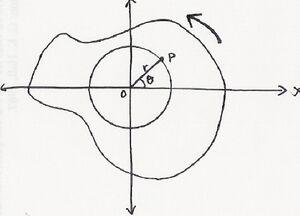
In the example illustrated to the right (or above in some mobile versions), a particle or body P is at a fixed distance r from the origin, O, rotating counterclockwise. It becomes important to then represent the position of particle P in terms of its polar coordinates (r, θ). In this particular example, the value of θ is changing, while the value of the radius remains the same. (In rectangular coordinates (x, y) both x and y vary with time). As the particle moves along the circle, it travels an arc length s, which becomes related to the angular position through the relationship:

[math]\displaystyle{ s = r\theta . }[/math]

Measurements

Angular displacement may be measured in radians or degrees. Using radians provides a very simple relationship between distance traveled around the circle and the distance r from the centre.

[math]\displaystyle{ \theta = \frac{s}{r} }[/math]

For example, if a body rotates 360° around a circle of radius r, the angular displacement is given by the distance traveled around the circumference - which is 2πr - divided by the radius: [math]\displaystyle{ \theta= \frac{2\pi r}r }[/math] which easily simplifies to: [math]\displaystyle{ \theta=2\pi }[/math]. Therefore, 1 revolution is [math]\displaystyle{ 2\pi }[/math] radians.

When a particle travels from point P to point Q over [math]\displaystyle{ \delta t }[/math], as it does in the illustration to the left, the radius of the circle goes through a change in angle [math]\displaystyle{ \Delta \theta = \theta_2 - \theta_1 }[/math] which equals the angular displacement.

Three dimensions

Figure 1: Euler's rotation theorem. A great circle transforms to another great circle under rotations, leaving always a diameter of the sphere in its original position.

Figure 2: A rotation represented by an Euler axis and angle.

In three dimensions, angular displacement is an entity with a direction and a magnitude. The direction specifies the axis of rotation, which always exists by virtue of the Euler's rotation theorem; the magnitude specifies the rotation in radians about that axis (using the right-hand rule to determine direction). This entity is called an axis-angle.

Despite having direction and magnitude, angular displacement is not a vector because it does not obey the commutative law for addition. Nevertheless, when dealing with infinitesimal rotations, second order infinitesimals can be discarded and in this case commutativity appears.

Several ways to describe angular displacement exist, like rotation matrices or Euler angles. See charts on SO(3) for others.

Given that any frame in the space can be described by a rotation matrix, the displacement among them can also be described by a rotation matrix. Being [math]\displaystyle{ A_0 }[/math] and [math]\displaystyle{ A_f }[/math] two matrices, the angular displacement matrix between them can be obtained as [math]\displaystyle{ \Delta A = A_f A_0^{-1} }[/math]. When this product is performed having a very small difference between both frames we will obtain a matrix close to the identity.

In the limit, we will have an infinitesimal rotation matrix.

Infinitesimal rotation matrices

This section is an excerpt from Infinitesimal rotation matrix[ edit ]

An infinitesimal rotation matrix or differential rotation matrix is a matrix representing an infinitely small rotation. While a rotation matrix is an orthogonal matrix [math]\displaystyle{ R^\mathsf{T} = R^{-1} }[/math] representing an element of [math]\displaystyle{ SO(n) }[/math] (the special orthogonal group), the differential of a rotation is a skew-symmetric matrix [math]\displaystyle{ A^\mathsf{T} = -A }[/math] in the tangent space [math]\displaystyle{ \mathfrak{so}(n) }[/math] (the special orthogonal Lie algebra), which is not itself a rotation matrix.

An infinitesimal rotation matrix has the form

[math]\displaystyle{ I + d\theta \, A, }[/math]

where [math]\displaystyle{ I }[/math] is the identity matrix, [math]\displaystyle{ d\theta }[/math] is vanishingly small, and [math]\displaystyle{ A \in \mathfrak{so}(n). }[/math]

For example, if [math]\displaystyle{ A = L_x, }[/math] representing an infinitesimal three-dimensional rotation about the x-axis, a basis element of [math]\displaystyle{ \mathfrak{so}(3), }[/math]

[math]\displaystyle{ dL_{x} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & -d\theta \\ 0 & d\theta & 1 \end{bmatrix}. }[/math]

The computation rules for infinitesimal rotation matrices are as usual except that infinitesimals of second order are routinely dropped. With these rules, these matrices do not satisfy all the same properties as ordinary finite rotation matrices under the usual treatment of infinitesimals. It turns out that the order in which infinitesimal rotations are applied is irrelevant.

See also

• Angular distance
• Angular position
• Angular velocity
• Infinitesimal rotation
• Linear elasticity
• Second moment of area

References

Sources

• Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2002), Classical Mechanics (third ed.), Addison Wesley, ISBN 978-0-201-65702-9 
• Wedderburn, Joseph H. M. (1934), Lectures on Matrices, AMS, ISBN 978-0-8218-3204-2, https://books.google.com/books?id=6eKVAwAAQBAJ