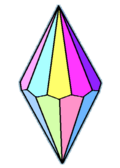
Decagonal trapezohedron
| Decagonal trapezohedron | |
|---|---|
| |
| Type | trapezohedra |
| Conway | dA10 |
| Coxeter diagram | |
| Faces | 20 kites |
| Edges | 40 |
| Vertices | 22 |
| Face configuration | V10.3.3.3 |
| Symmetry group | D10d, [2+,20], (2*10), order 40 |
| Rotation group | D10, [2,10]+, (2.2.10), order 20 |
| Dual polyhedron | Decagonal antiprism |
| Properties | convex, face-transitive |
In geometry, a decagonal trapezohedron (or decagonal deltohedron) is the eighth in an infinite series of face-uniform polyhedra which are dual polyhedra to the antiprisms. It has twenty faces which are congruent kites.
It is a isohedral figure, (face-transitive), having all its faces the same. More specifically, all faces must be not merely congruent but must be transitive, i.e. must lie within the same symmetry orbit. Convex isohedral polyhedra are the shapes that will make fair dice.[1]
Symmetry
The symmetry a decagonal trapezohedron is D10d of order 40. The rotation group is D10 of order 20.
Variations
One degree of freedom within symmetry from D10d (order 40) to D10 (order 20) changes the congruent kites into congruent quadrilaterals with three edge lengths, called twisted kites, and the trapezohedron is called a twisted trapezohedron.
If the kites surrounding the two peaks are not twisted but are of two different shapes, the trapezohedron can only have C10v (cyclic) symmetry, order 20, and is called an unequal or asymmetric decagonal trapezohedron. Its dual is an unequal antiprism, with the top and bottom polygons of different radii. These are still isohedral.
If the kites are twisted and of two different shapes, the trapezohedron can only have C10 (cyclic) symmetry, order 10, and is called an unequal twisted decagonal trapezohedron.
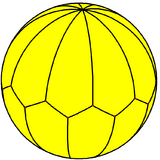
Spherical tiling
The decagonal trapezohedron also exists as a spherical tiling, with 2 vertices on the poles, and alternating vertices equally spaced above and below the equator.
See also
References
- ↑ McLean, K. Robin (1990), "Dungeons, dragons, and dice", The Mathematical Gazette 74 (469): 243–256, doi:10.2307/3619822.
External links
- Weisstein, Eric W.. "Trapezohedron". http://mathworld.wolfram.com/Trapezohedron.html.
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra